physics.zfftt.kpi.ua

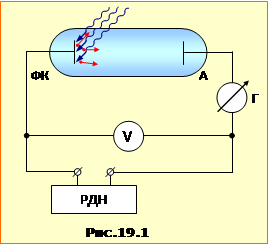
Одним із явищ, які доводять квантову природу світла, є фотоефект – звільнення електронів від зв'язку з атомами речовни під дією світла. Розрізняють зовнішній та внутрішній фотоефект. У першому випадку звільнені електрони виходять за межі тіла, а в другому лишаються всередині.

Закономірності фотоефекту можна встановити, досліджуючи вольт-амперні характеристики ВАХ (залежність струму від напруги I(U)) вакуумного фотодіода за різних умов опромінювання світлом.

Примітка. Вакуумний фотодіод – це електронна лампа, що має два електроди: анод А і світлочутливий холодний (неророзжарюваний) фотокатод ФК який опромінюється світлом. 

Для вимірювання ВАХ на фотодіод від регульованого джерела напруги (РДН) за схемою рис.19.1 подають напругу U, полярність і величину котрої можна змінювати й вимірювати вольтметром V.  Фотострум I, який з'явлється при опроміненні катода, реєструється гальванометром (чутливим амперметром) Г.

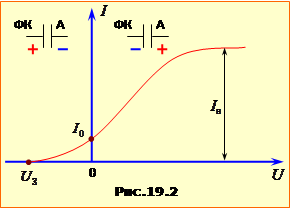
Загальний вигяд ВАХ фотоелемента показано на рис.19.2, на якому область \(U>0\) відповідає прямій (прискорювальній для електронів), а  \(U<0\) –  зворотній(гальмівній) напрузі для фотоелектронів.

Показаний графік залежності I(U) висвітлює головні властивості фотоефекту. А саме:

1. При підвищенні напруги на фотоелементі зростання струму з певного моменту починає вповільнюватись і припиняється взагалі при деякому струмі I = I_н, що називається ″струмом насичення″.

Описана форма ВАХ має наступне пояснення. Електрони вилітають з катода по всіх напрямах, тож при U = 0 лише частина з них потрапляє на анод, створючи невеликий струм  І₀. Коли ж на фотоелементі починає зростати пряма напруга \(U>0\), то все більша й більша частина фотоелектронів спрямовується електричним полем на анод, і струм істотно зростає. Але  електрони вириваються з катода не електричним полем, а світлом, тому з певного моменту починають потрапляти на анод, і настає ″насичення струму″. При цьому його величина

де n – кількість електронів, що вириваються світлом з фотокатода за одиницю часу, і \(e=1,6\cdot{10}^{-19}\) Кл – елементарний заряд.

2. При \(U\le{0}\) у фотоелементі теж тече струм \(I\le{I₀}\), для припинення котрого на фотоелемент треба подати гальмівну напругу найменшої необхідної величини U_з, яка називається  ″запірною напругою″.

Наявність струму при напрузі \(U\le{0}\) пояснюється тим, що фотоелектрони вилітають з катода з деякою початковою швидкістю та кінетичною енергією і, якщо вона є достатньою для виконання роботи (Ч. 3, (1.13а)) по подоланню гальмівного поля, потрапляють на анод.  Отож, запірна напруга задовольняє умову 

де v – найменша швидкість вильоту електронів із фотокатода, при якій вони здатні дістатися анода.

Із результатів дослідження ВАХ фотоелементів із катодами з різних металів і при різних умовах опромінення випливають наступні загальні закономірності зовнішнього фотоефекту:

1. Кількість електронів, що вилітають із металу за одиницю часу під дією світла, є прямо пропорційна його інтенсивності й не залежить частоти.

2. Максимальна кінетична енергія фотоелектронів лінійно залежить від частоти опромінювального світла й не залежить від його інтенсивності.

3. Для кожного металу існує своя червона межа фотоефекту – мінімальна частота \(\nu_{0}\) (або максимальна довжина хвилі \(\lambda_{0}\)) опромінювального світла, при якій є можливий фотоефект.

Окрім цього було встановлено безінерційність фотоефекту, тобто те, що фотострум з'являється практично одночасно з початком опромінювання (із затримкою \(\tau\sim{10}^{-9}\) с).

Прикметно, що жодну з наведених закономірностей неможливо пояснити на основі класичних уявлень. Приміром, якщо світло трактувати як неперервну хвилю, то кінетична енергія фотоелектронів, отож і запірна напруга фотоелемента (п. 2), має залежати від  інтенсивності світла, тоді як у дійсності вона визначається тільки його частотою. Так само кількість фотоелектронів і струм насичення (п. 1) мали би бути прямо пропорціні частоті світла, а насправді вона залежить тільки від його інтенсивност.

У той же час описані закономірності вичерпно пояснюються квантовою теорією фотоефекту, створеною Ейнштейном, згідно з якою в кожному елементарному акті фотоефекту

При цьому для виходу назовні електрон має подолати зв'язок із кисталічною ґраткою металу, витративши  для цього енергію, що називається роботою виходу A і є його табличною характеристикою. Тож, кінетична енергія фотоелектрона при вильоті складає

W = ε – A,

де ε – енергія поглинутого фотона.

Якщо в цьому співвідношенні вирази кінетичної енергії та енергії фотона запишемо розгорнуто, то отримаємо наступні вирази рівняння Ейнштейна для зовнішнього фотоефекту:

1. Через квантову природу світла при його поглинанні електрон потрібну для виконання роботи виходу енергію не поступово накопичує, а отримує одразу. Цим пояснюється безінерційність фотоефекту.

2. З рівнянь (2.7) і (2.7б) прямо випливає висновок про лінійну залежність кінетичної енергії фотоелектрона від частоти опромінюючого світла.

3. З рівнянь (2.7) і (2.7a) очевидно, що вихід електрона з металу є можливий тільки за умови \(h\nu\ge{A}\) або \(hc/\lambda\ge{A}\), тобто при частоті світла

$\nu =\frac{A}{h}$,     або      $\lambda \le \frac{hc}{A}$   

Це пояснює існування червоної межі фотоефекту – мінімальної частота (максимальної довжини хвилі) світла, що спроможне виривати електрони з металу.

І останнє. Відповідно до квантових уявлень, інтенсивність світла I (енергія, що переноситься за одиницю часу через одиницю площі) є прямо пропорційна відповідній кількості фотонів:

де ε – енергія одного фотона, \(\Delta{S}_{\perp}\) – площа опромінюваної поверхні, що є перпендикулярна до напрямку променів, \(\Delta{N}\) – кількість фотонів, які падають на поверхню \(\Delta{S}_{\perp}\) за час \(\Delta{t}\), n – те саме за 1с. Очевидно, що кількість електронів n_e, які вириваються світлом за одиницю часу, є так само прямо пропорційна величині n. Цим пояснюється перша з розглянутих на початку закономірностей зовнішнього фотоефекту – пряма пропорційна залежність між кількістю вирваних електронів та інтенсивністю опромінювального світла.