ФІЗИКА. Вчимося розв'язувати задачі. "СУЧАСНА ФІЗИКА". Компенсаційний курс
2. Приклади розв'язування задач
У даному й наступному пунктах по замовчуванню прийнято таке.
1. Означення ''релятивістський'' без необхідності не використовується.
2. Система відліку, в якій тіло (стрижень, або частинка) перебуває в спокої називається ''власною'', а та, в якій воно рухається – ''лабораторною''.
3. Параметри та характеристики руху тіла, що подано як ''власні'', або без означення, відносяться до власної системи відліку.
4. Рухи тіл розглядаються в системах координат із співнапрямреними осями ординат та збіжними осями абсцис і здійснюються паралельно до останніх.
Задача 1.1. Рухомий стрижень довжиною $l$ = 100 см, який спрямовано під кутом \(\theta=45^{\circ}\) до напрямку руху, має швидкість $v=c/2$. Визначити довжину ${{l}_{0}}$ та орієнтацію (кут ${{\theta }_{0}}$) стрижня у власній системі відліку.
Задача 1.2. Визначити довжину вільного пробігу ${{l}}$ нестабільної частинки із часом життя \(\Delta{t}\) = 20 нс, якщо її власний час життя $\Delta {{t}_{0}}$ є вдвічі менший.
Задача1.3. Дві частинки рухаються назустріч одна одній зі швидкостями v1 = 0,50c і v2 = 0,75c. Визначити: А) відносну швидкість частинок vв та Б) швидкість їхнього зближення u.
Задача 1.4. Визначити, на скільки η (%) відрізняється від с швидкість протона з імпульсом $\tilde{p}$ = 10,0 ГеВ/с, якщо його енергія спокою E0 = 938,3 МеВ.
Задача 1.5. Визначити імпульс p протона (енеогія спокою E0 = 238,3 Мев) при кінетичній енергії T = 500 МеВ.
Задача 1.6. Без урахування втрат в атмосфері на одиницю площі перпендикулярної до сонячних променів поверхні Землі за одинцю часу падає енергія I = 1,4 кДж/(м2·с). Взявши до уваги середній радіус земної орбіти R = 149,5·106 км і масу Сонця M = 2·1030 кг, визначити: А) щосекундну втрату Сонцем маси μ (кг/с) та Б) час T, за який воно мало би ''полегшати'' на η = 1 % при незмінній величині I.
Задача 1.1
Рухомий стрижень довжиною $l=100$ = 100 см, який спрямовано під кутом \(\theta=45^{\circ}\) до напрямку руху, має швидкість $v=c/2$.
Визначити
довжину ${{l}_{0}}$ та орієнтацію (кут ${{\theta }_{0}}$) стрижня у власній системі відліку.
|
Дано: $v=c/2$
${{l}}$ =100 см
\(\theta=45^{\circ}\)
|
|
l0 - ?,
${{\theta }_{0}}$ - ? |
Розв’язання
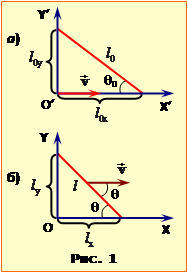 Довжина стрижня l0 у пов'язаній з ним власній системі відліку X′O′Y′ (рис.1а) визначається його проєкцями, як
Довжина стрижня l0 у пов'язаній з ним власній системі відліку X′O′Y′ (рис.1а) визначається його проєкцями, як
|
${{l}_{0}}=\sqrt{l_{{{0x}'}}^{2}+l_{{{0y}'}}^{2}}$, |
(1) |
При цьому, внаслідок скорочення довжин у напрямку руху (п. 1.2), проєкції ${l_{{0x}'}}$, ${l_{{0y}'}}$ є пов'язані такими в лабораторній системі відліку співвідношеннями (1.1):
| ${{l}_{0{x}'}}=\frac{{{l}_{x}}}{\sqrt{1-{{\beta }^{2}}}},\quad \quad {{l}_{0{y}'}}={{l}_{y}}$, |
(2) |
де \(l_{x}=l\cos\theta\), \(l_{y}=l\sin\theta\).
Отже,
| ${{l}_{0}}=l\sqrt{\frac{{{\cos }^{2}}\theta }{1-{{\beta }^{2}}}+{{\sin }^{2}}\theta }$ |
|
У цьому виразі має сенс зробити підстановку ${{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta $ й після спрощень, записати відповідь у більш компактному й зручному для обчислень вигляді:
| \(l_{0}=l\sqrt{\frac{1-\beta^{2}\sin^{2}\theta}{1-\beta^{2}}}\). |
|
З урахуванням заданого значення β = 0,5, числова відповідь складає
\(l_{0}\) = 108 см.
Другу шукану величину ${{\theta }_{0}}$ знайдемо, взявши до уваги відсутність скорочення довжин у поперечному до руху стрижня напрямі. Тож
${{l}_{0y}}={{l}_{y}}=l\sin \theta$ $\Rightarrow $ $\sin {{\theta }_{0}}=\frac{l}{{{l}_{0}}}\sin \theta $,
звідки
$\sin {{\theta }_{0}}$ = 0,655 $\Rightarrow $ ${{\theta }_{0}}$ = 40,9°.
Задача 1.2
Визначити
довжину вільного пробігу ${{l}}$ нестабільної частинки із часом життя $\Delta {{t}}$ = 20 нс, якщо її власний час життя $\Delta {{t}_{0}}$ є вдвічі менший.
|
Дано: $\Delta {{t}}$ = 20 нс
$\Delta {{t}_{0}}$ = $\Delta {{t}}$/2
|
|
${{l}}$ - ?
|
Розв’язання
Довжина вільного пробігу нестабільної частинки – це відстань, яку вона встигає пройти в лабораторній системі відліку за час життяі з часом життя, рухаючись із певною швидкістю $v$:
${{l}}$ = $v$$\Delta {{t}}$ = $\beta c\cdot \Delta t$,
де \(\beta=v/c\).
Тож, аби отримати відповідь, треба визначити параметр $\beta$. Це легко зробити за допомогою співвідношення (1.2), з якого випливає, що
$1-{{\beta }^{2}}={{\left( \frac{\Delta {{t}_{0}}}{\Delta t} \right)}^{2}}\quad \Rightarrow \quad \beta =\sqrt{1-{{\left( \frac{\Delta {{t}_{0}}}{\Delta t} \right)}^{2}}}\quad $.
Відтак, підставивши це значення у вираз (1), дістанемо наступну відповідь:
$l=c\sqrt{\Delta {{t}^{2}}-\Delta t_{0}^{2}}$ = 5,2 м.
Задача 1.3
Дві частинки рухаються назустріч одна одній зі швидкостями v1 = 0,50c і v2 = 0,75c.
Визначити:
А) відносну швидкість частинок vв та
Б) швидкість їхнього зближення u.
|
Дано: v1 = 0,50c
v2 = 0,75c
|
|
vв - ?
u - ?
|
Розв’язання
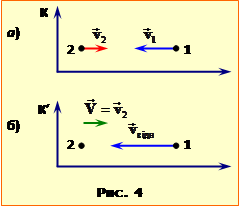
Аби уникнути непорозумінь, уточнимо смисл величин, які належить визначити, а саме. Відносна швидкість є швидкістю руху одного тіла відносно іншого, нехай першого відносно другого. Тоді, якщо з тілом 2 пов'язати систему відліку K′ (рис. 4б), то вона матиме швидість $\vec{V}={{\vec{v}}_{2}}$, тіло 2 в ній перебуватиме в спокої, а тіло 1 рухатиметься із шуканою швидкістю ${{\vec{v}}_{в}}$:
${{{\vec{v}}'}_{1}}={{\vec{v}}_{в}}$.
Натомість швидкість зближення $u$ – то є швидкість зміни відстані між тілами для стороннього спостерігача в нерухомій системі відліку K, рис. 4а. З урахуванням сказаного визначення величин ${{v}_{в}}$ і $u$ не становить труднощів.
A) Значення відносної швидкості vв дорівнює взятій із зворотнім знаком проєкції швидкості першої частинки в K′- системі відліку (рис. 4б) й визначається формулою (1.3а) при \(v_{x}^{{′}}=-{{v}_{в}}\) і $V={{v}_{2}}$:
${{v}_{в}}=\frac{{{v}_{1}}+{{v}_{2}}}{1+\left( {{v}_{1}}\cdot {{v}_{2}} \right)/{{с}^{2}}}=0,91c$
Зауважимо, що при v1 = v2 = c (частинки – фотони), їхня відносна швидкість складала б
${{v}_{в}}=\frac{c+c}{1+\left( c\cdot c \right)/{{с}^{2}}}=c$
у згоді з твердженням про існування в Природі граничної швидкості руху.
Б) У лабораторній системі відліку К частинки за час t проходять відстані l1 = v1t і l2 = v2t, наближаючись одна до одної на відстань l = v1t + v2t = (v1 + v2)t зі швидкістю
\(u=\frac{l}{t}=v_{1}+v_{2}=1,25c\).
Те, що вийшло u > с може видатися парадоксальним, але нічого дивного в цьому результаті немає: адже величина u визначає швидкість зміни відстані між частинками для стороннього спостерігача й не є швидкістю руху однієї частинки відносно іншої.
Задача 1.4
Визначити,
відрізняється від с швидкість протона з імпульсом $\tilde{p}$ = 10,0 ГеВ/с, якщо його енергія спокою E0 = 938,3 МеВ.
|
Дано: $\tilde{p}$ = 10,0ГеВ
E0 = 938,3МеВ
|
|
η (%) - ?
|
Розв’язання
Перед розв'зуванням візьмемо до уваги таку довідку. Елементарні частинки мають гранично малу масу, тому для них, навіть при навколосвітньої швидкостях руху, основні одиниці енергії (Дж) й імпульсу (кг·м/с) є несумірно великі. Тож зазвичай вживають позасистемні одиниці енергії: електрон-вольт (1 еВ = \(1,6\cdot{10}^{-19}\) Дж), мега електрон-вольт (1 МеВ = \(10^{6}\) еВ, читається ''мев'', ) та гіга електрон-вольт ''гев'' (А1 ГеВ = \(10^{9}\) еВ). А для імпульсу використовують умовну одиницю 1 ГеВ/с, де с означає не секунду, а швидкість світла. Розмірністю такої одиниці, як і належить, є (кг·м/с), але числове значення $\tilde{p}$ заданого так імпульсу насправді дорівнює його добутку на швидкість світла: $\tilde{p}$ = (рс).
Шукана відносна відміна швидкості частинки v від швидкості світла с складає
|
\(η=\frac{c-v}{c}=1-\beta\), де $\beta =\left( v/c \right)$. |
(1) |
Отже, для отримання відповіді треба визначити параметр \(\beta\). Для цього використаємо вираз релятивістського імпульсу (1.5), зробивши в ньому заміну $v=c\beta $:
$p=\frac{{{m}_{0}}c\beta }{\sqrt{1-{{\beta }^{2}}}}$.
Далі домножимо обидві частини отриманої рівності на c та за формулою (1. 7б) зробимо підстановку ${{m}_{0}}=\left( {{E}_{0}}/{{c}^{2}} \right)$ і дістанемо:
$pc=\frac{{{E}_{0}}\beta }{\sqrt{1-{{\beta }^{2}}}}$,
або
$\frac{\beta }{\sqrt{1-{{\beta }^{2}}}}=\gamma $, де $\gamma =\frac{pc}{{{E}_{0}}}$.
Звідси отримаємо
$\beta =\frac{1}{\sqrt{1+{{\gamma }^{2}}}}$
і за виразом (1) знайдемо загальну відповідь
$\eta =1-\frac{1}{\sqrt{1+{{\gamma }^{2}}}}$
та після обрахунків (без округлення) числове значення:
$\eta$ $\approx $ 0,44%.
Задача 1.5
Визначити
імпульс p протона (енергія спокою E0 = 238,3 Мев) при кінетичній енергії T = 500 МеВ.
|
Дано: E0 = 238,3 Мев T = 500 МеВ
|
|
p - ?
|
Розв’язання
Імпульс і кінетична енергія є взаємозумовленими характеристиками руху тіла, але для релятивістських (надшвидких) частинок прямого зв'язку між ними немає. Проте його можна встановити через вирази енергії (1.7) і (1.7а), з яких випливає, що
|
$m{{c}^{2}}\left( 1-\frac{{{v}^{2}}}{{{c}_{2}}} \right)={{m}_{0}}{{c}^{2}}$. |
(1) |
Тож, якщо піднести отриманий вираз до квадрата, вийде:
\(m^{2}c^{4}=\frac{m_{0}^{2}c^{4}}{1-\beta^{2}}\) \(\Rightarrow\) \(m^{2}c^{4}-m^{2}v^{2}c^{2}=m_{0}^{2}c^{4}\).
В отриманій рівності \(m_{0}c^{2}=E_{0}\) – енергія спокою і mv = p – релятивістський імпульс, отже, маємо:
|
\(E^{2}-p^{2}c^{2}=E_{0}^{2}\) \(\Rightarrow\) \(p=\frac{1}{c}\sqrt{E^{2}-E_{0}^{2}}\). |
(2) |
Відтак зробимо очевидну підстановку E2 = (E0 + T)2, і, розкривши дужки, отримаємо загальну відповідь:
\(p=\frac{1}{c}\sqrt{T(T+2E_{0})}\).
Числове значення в одиницях СІ складає
p = 5,8·10–19 кг·м/с,
а в (ГеВ/с) (див. попередню задачу)
p = 1,09 ГеВ/с.
Задача 1.6
Без урахування втрат в атмосфері на одиницю площі перпендикулярної до сонячних променів поверхні Землі за одиницю часу падає енергія I = 1,4 кДж/(м2·с). Взявши до уваги середній радіус земної орбіти R = 149,5·106 км і масу Сонця M = 2·1030 кг,
визначити:
А) щосекундну втрату Сонцем маси μ (кг/с) та
Б) час T, за який воно мало би ''полегшати'' на η = 1 % при незмінній величині I.
|
Дано: I = 1,4 кДж/(м2·с) = 1,4·103 Дж/(м2·с)
R = 149,5·106 км = 1,495·1011 м
M = 2·1030 кг
η = 1 %
|
|
μ - ?, Т - ?
|
Розв’язання
А) Згідно із співвідношенням (1.7б), маса Сонця зменшується з часом зі швидкістю
|
$\mu =\frac{W}{{{c}^{2}}}$, |
(1) |
де W – інтенсивність, тобто, енергія, що випромінюється Сонцем за 1 c.
Зрозуміло, що випромінювання Сонця є однакове по всіх напрямках, отож для спостерігача на Землі його енергія з однаковою щільністю I розподіляється по поверхні сфери радіуса земної орбіти R. Отже,
$W=I\cdot 4\pi {{R}^{2}}$,
і щосекундна втрата маси Сонця складає
$\mu =\frac{4\pi {{R}^{2}}I}{{{c}^{2}}}$.
Відповідно, задана зміна маси Сонця на величину $\Delta M=\eta M$ відбулася б за час
$T=\frac{\eta M{{c}^{2}}}{4\pi {{R}^{2}}I}$.
Обчислення дають
\(\mu\approx4,3\cdot{10}^{9}\) кг/с
і
\(T=4,65\cdot{10}^{18}\) c,
що складає приблизно 150 мільярдів років.