physics.zfftt.kpi.ua

Однаковість швидкості світла у вакуумі в усіх системах відліку означає, що класична формула додавання швидкостей (1.9) є принципово  не вірна. Тож у СТВ при переході від однієї інерційної системи відліку до іншої  швидкість тіла змінюється за своїм законом, який є досить складний і на загал не може бути записаний безпосередньо через вектор швидкостуй. Тож розглянемо окремий випадок (рис.18.2), коли системи відліку XOY та X′O′Y′ мають осі X, X′ та Y, Y′, відповідно, одного напрямку й рухаються одна відносно одної вздовж осей X, X′ зі сталою швидкістю V. 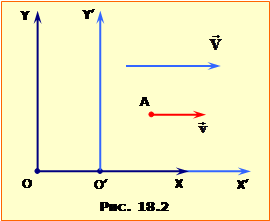В такому випадку при русі тіла (точка А) вздовж того самого напрямку зв'язок між його швидкостями визначається наступним релятивістським законом додавання швидкостей:

де \(v_{x}\),  \(v_{x}^{\prime}\) – проєкція швидкості у відповідній системі відліку.

В отриманих результатах варто зупинитися на двох моментах:

1. У виразах (18.3), (18.3а) при швидкостях(\(v_{x}\ll{c}\), \(V\ll{c}\)) виходить \(v_{x}V/c^{2}\ll{1}\), \(v_{x}^{\prime}V/c^{2}\ll{1}\), і релятивістські формули (18.3), (18.3а) переходять у  класичні (1.9) і (1.10):

\(v_{x}=v_{x}^{\prime}+V\),

\(v_{x}^{\prime}=v_{x}-V\).

2. За будь-якої швидкості тіла ${{v}_{x}}^{\prime }$ та системи відліку V виходить  \(v_{x}\le{c}\) (див. задачу 18.4). Зокрема, якщо ${{v}_{x}}^{\prime }=c$, то й \(v_{x}={c}\). Отже,  релятивістський закон додавання швидкостей узгоджується з постулатом сталості швидкості світла у вакуумі, тобто існуванням у Природі граничної швидкості c.