|
Уявлення класичної фізики відповідають нашому життєвому досвіду і здаються самоочевидними. Але вони несумісні з постулатами СТВ, з яких випливає, що поняття відстані між точками (довжини тіла) і проміжку часу між подіями (тривалості процесу) – відносні. Це виявляється в ефектах скорочення довжин і уповільнення часу:
|
Лінійні розміри тіла скорочуються в напрямку руху відповідно до формули:
|
|
\(l=l_{0}\sqrt{1-\frac{v^{2}}{c^{2}}}=l_{1}\sqrt{1-\beta^{2}}\),
|
(18.1)
|
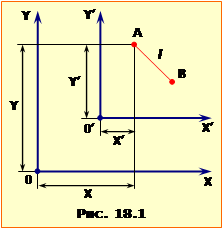
де \(l_{0}\) – власна довжина, тобто довжина нерухомого відносно спостерігача тіла, під яким розуміють стержень, зорієнтований уздовж осей X, X¢ системи відліку, l – лабораторна довжина, тобто довжина того ж тіла під час його руху зі швидкістю v, напрямленою по довжині тіла, c – гранична швидкість, яка дорівнює швидкості світла у вакуумі (\(c=3\cdot{10}^{8}\) м/с), \(\beta=v/c\).
Поперечні відносно напрямку руху розміри тіл не змінюються.
Проміжки часу теж відрізняються в різних системах відліку:
|
\(\Delta{t}=\frac{\Delta{t}_{0}}{\sqrt{1-v^{2}/c^{2}}}=\frac{\Delta{t}_{0}}{\sqrt{1-\beta^{3}}}\),
|
(18.2)
|
де \(\Delta{t}_{0}\) – власний проміжок часу, тобто проміжок часу між двома подіями, що відбуваються в деякій фіксованій точці А, який виміряний годинником, розташованим у тій же точці; \(\Delta{t}\) – лабораторний проміжок часу, тобто проміжок часу між цими подіями, визначений у системі відліку, відносно якої точка А рухається зі швидкістю v.
З формули (18.2) видно, що завжди \(\Delta{t}\ge\Delta{t}_{0}\), тобто проміжок часу (тривалість процесу) у нерухомій для спостерігача фізичній системі завжди менший, ніж для спостерігача, відносно якого система рухається. Іншими словами, темп часу різний у різних системах відліку. Наприклад, для космонавтів у міжзоряній ракеті час тече повільніше, ніж для земних спостерігачів. Тому говорять про уповільнення часу в системах відліку, що рухаються.
Усе сказане означає відносність простору і часу, тобто, що
|
не існує світового простору і єдиного світового часу. Просторові і часові масштаби в різних системах відліку різні.
|
Формули (18.1) і (18.2) втрачають фізичний зміст при \(v\ge{c}\). Це є формальним вираженням існування в природі граничної швидкості c.
При \(v/c\to{0}\) ці формули дають "класичні" співвідношення l = l0 і \(\Delta{t}=\Delta{t}_{0}\). Це стосується і всіх інших співвідношень механіки СТВ. У дійсності такий "перехід до класичної механіки" відбувається при дуже великих швидкостях. Наприклад, навіть при v = 30000 км/с довжини тіла, що рухається і нерухомого тіла ще майже не відрізняються: l = 0,995l0. Тому при швидкостях руху, з якими має справу класична механіка, ефекти СТВ не проявляються.
|