ФІЗИКА. Вчимося розв'язувати задачі. "СУЧАСНА ФІЗИКА". Компенсаційний курс
Розділ I. Спеціальна теорія відносності
1.2. Відносність довжин і проміжків часу
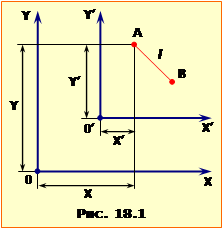
Зрозуміло, що положення тіла в просторі є відносне й визначається системою відліку. Але сам простір у класичній фізиці розглядається як абсолютний – єдиний для усього Всесвіту й однаковий за властивостями незалежно від системи відліку. З такої концепції випливає самоочевидний висновок: хоча в ріних системах відліку XOY і X′O′Y′ (рис.18.1) координати заданої точки відрізняються (\(X\ne{X}^{\prime}\), \(Y\ne{Y}^{\prime}\)), відстань l між двома точками, приміром, кінцями жорсткого срижня АВ, є однаковою в усіх системах відліку. Тим стверджується, що взаємне розташування точок тіла, тож його розміри й форма не залежать від системи відліку, тобто є абсолютними.
|
Абсолютним вважається й час. А саме, хоча моменти часу, в які відбулася якась подія, в різних місцях (часових поясах) виражаються різними числами, видається самоочевидним, що проміжок часу між двома подіями є абсолютним, тобто однаковим для всього Всесвіту. Такі уявлення лежать в основі класичної механіки й відповідають нашому життєвому досвіду. Але є несумісні з постулатами СТВ, з яких випливає, що відстані між точками і проміжку часу між подіями є відносні, залежніі від системи відліку. Одним із проявів цього є ефект скорочення довжин, який полягає в тому, що поздовжня довжина l тіла – стрижня, що рухається в поздовжньому напрямі із швидкістю v (рис.18.1), дорівнює
де \(l_{0}\) – власна довжина стрижня, тобто, відстань \(\Delta{Δx′}\) між кінцями у власній системі відліку X′O′Y′, де він перебуває в спокої. Відповідно, систему XOY, в якій стрижень рухається, називають лабораторною системою відліку, а l – лабораторною довжиною. Указане скорочення стосується лише поздовжніх відстаней. Тож, при довільній орієнтації срижня відносно напрямку руху різниця поперечних координат його кінців в обох системах відліку однакова: \(\Delta{Δy}\) = \(\Delta{Δy′}\). Проміжки часу між двома подіями в деякій точці А, що виміряні в двох різних системах відліку, теж відрізняються й пов'язані співвідношенням:
де \(\Delta{t}_{0}\) – власний проміжок часу, тобто такий, що виміряний нерухомим відносно т. А годинником. Відповідно, \(\Delta{t}\) – лабораторний проміжок часу, тобто такий, що виміряний спостерігачем (годинником) лабораторній системі відліку, яка рухається відносно т. А зі швидкістю v. Згідно з формулою (18.2) \(\Delta{t}\ge\Delta{t}_{0}\), тобто проміжок часу (тривалість процесу) у власній системі відліку подій є менший, ніж у лабораторній, в якій ''події рухаються''. Це означає, що час у різних системах відліку протікає не однаково. Приміром, для спостерігача на Землі він спливає швидше, ніж для космонавтів у міжзоряній ракеті. В цьому полягає ефект уповільнення часу в рухомих системах відліку. Усе сказане означає відносність простору й часу, тобто, що
Окрім того, при \(v\ge{c}\) вирази (18.1) і (18.2) втрачають фізичний зміст, що є формальним ознакою існування в природі граничної швидкості c. Все сказане вище може справити враження, що класична механіка Ньютона та релятивістська механіка Ейнштейна є несумісні. Але це не так, і при \(v/c\to{0}\) з формул (18.1) і (18.2) випливає звичне l = l0 і \(\Delta{t}=\Delta{t}_{0}\). Тож класична кінематика є граничним випадком релятивістської. Варто також зауважити, що на практиці відміна між двома механіками стає помітною лише при неможливихдосяжних для макроскопічних тіл швидкостях. До прикладу, за співвідношеннями (18.1) і (18.2) навіть при швидкості v = 30000 км/с довжина рухомого тіла зменшується тільки на 0,5%. Тому в СТВ термін ''тіло'', реально означає ядра атомів та елементарні частинки, для яких субсвітлові швидкості є досяжні. |