ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
Приклади розв'язування задач
Задача 17.5
Монохроматичне світло нормально падає на дифракційну гратку, яка має 45 штрихів на кожний міліметр довжини. Кут між напрямками на максимуми другого (m1 = 2) та третього (m2 = 3) порядків \(\Theta=1,6^{\circ}\).
Визначити
довжину хвилі світла \(\lambda\).
|
Дано: N = 45 1/мм
m1 = 2
m2 = 3
Θ = 1,6°
|
|
λ - ?
|
Розв’язання
Відповідно до умови головних максимумів дифракційної гратки (формула (17.9)), і з урахуванням умови задачі для максимумів порядку m1 і m2 можна записати:
|
|
\(\d\sin\varphi=m_{1}\lambda\), |
(1) |
|
|
\(\d\sin(\varphi+\Theta)=m_{2}\lambda\), |
(2) |
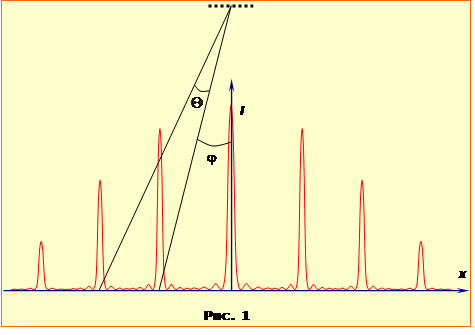
де \(\varphi\) – кут між нормаллю до ґратки і напрямком на максимум порядку m1 (рис.1), d – період гратки, що зв'язаний з числом штрихів на одиницю довжини співвідношенням
\(d=\frac{1}{N}\).
Представимо вираз (2) у вигляді
|
|
\(\frac{m_{2}\lambda}{d}=\sin\varphi\cos\Theta+\sin\Theta\cos\varphi\). |
(3) |
Оскільки кут \(\Theta\ll{1}\) (1,6° = 0,028 рад), то можна прийняти \(\cos\Theta=1\) та \(\sin\Theta=\Theta\) (рад). Крім того
\(\cos\varphi=\sqrt{1-\sin^{2}\varphi}\).
Зробивши ці підстановки у вираз (3), одержимо
\(\frac{m_{2}\lambda}{d}=\sin\varphi+\Theta\sqrt{1-\sin^{2}\varphi}\).
Підставивши вираз \(\sin\varphi=m_{1}\lambda/d\) з формули (1) в останній вираз, після перетворень знаходимо:
\(\lambda=\frac{\Theta}{N\sqrt{(m_{2}-m_{1})^{2}+m_{1}^{2}\Theta}}=\frac{\Theta}{N\sqrt{1+\Theta^{2}}}\approx\frac{\Theta}{N}\).
Обчислення дають:
\(\lambda=\frac{0,028}{45}\approx{620}\) нм.