ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
| Site: | physics.zfftt.kpi.ua |
| Course: | physics.zfftt.kpi.ua |
| Book: | ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс |
| Printed by: | |
| Date: | Thursday, 19 February 2026, 9:24 AM |
Table of contents
СВІТЛО (Вступ)
|
Оптика – це наука про світло – електромагнітне випромінювання, котре створює зорове відчуття в оці людини та інших живих істот. Світло має двоїсту природу й залежно від умов виявляє себе або як хвиля, або як потік елементарних частинок – фотонів (світлових квантів). Деякі хвильові прояви світла розглянуто в розділах: кожний з яких включає: 2. Приклади розв’язування задач 3. Задачі для самостійної роботи Як говорилося раніше (Частина [4]), у природі, крім механічних, спостерігаються електромагнітні хвилі (ЕМХ), тобто, розповсюдження взаємозалежних коливань електричного та магнітного полів. На відміну від механічних, електромагнітні хвилі можуть існувати у вакуумі й поширюються в ньому зі швидкістю
яка ні від чого не залежить і є однією з фундаментальних фізичних констант. У речовині швидкість ЕМХ зменшується й визначається її електричними та магнітними властивостями. При цьому прозорими для світла є тільки деякі немагнітні діелектрики, тож швидкість світла практично залежить тільки від їхньої діелектричної проникності ε (див [3], п. 1.1), як
де величина
називається абсолютним показником заломлення, або оптичною густиною речовини. Електромагнітні хвилі створюють зорове відчуття в вузькому спектральному інтервалі, який для людини усереднено складає: \(\nu=(0,75\div{0,4})\cdot{10^{15}}\) Гц у частотах і \(\lambda=(0,4\div{0,75})\cdot{10^{-6}}\) м. у довжинах хвилі у вакуумі (або повітрі). Випромінювання в прилеглих діапазонах має близькі властивості й досліджується тими самими методами, тому теж називається світлом: ультрафіолетовим (при \(\nu\gt{0,75\cdot{10^{15}}}\) Гц; \(\lambda_{0}\lt{10^{-6}}\) м) та інфрачервоним (при \(\nu\lt{0,4}\cdot{10^{15}}\) Гц; \(\lambda_{0}\gt{0,75}\cdot{10^{15}}\) м). Відповідно, ультрафіолетове, видиме та інфрачервоне випромінювання сукупно утворюють оптичний діапазон електромагнітного спектра. (Принагідно зауважимо, що в текстах довжину світлової хвилі зазвичай виражають у мікрометрах (1 мкм = 10–6 м), або нанометрах (1 нм = 10–9 м)). Подібно до звуку, що суб'єктивно сприймається через гучність і висоту тону, світло при потраплянні в око характеризується яскравістю, мірою якої є інтенсивність ([4], ф-ла (3.8)), і кольором, який визначається частотою світлової хвилі й при її збільшенні неперервно змінюється від червоного до фіолетового. Тож усю гаму кольорів умовно поділяють на сім діапазонів – "кольорів веселки": червоний, помаранчевий, жовтий, зелений, блакитний, синій і фіолетовий. При цьому, хоча людина не може відрізнити колір променів світла із дуже близькими частотами, вона розрізняє багато відтінків основних кольорів.
|
Розділ I. Геометрична оптика
|
Дослід свідчить, що в однорідному середовищі світло, як і інші хвилі, розповсюджується прямолінійно, а на межі різних середовищ змінює напрям поширення у згоді із простими законами геометричної оптики, на яких ґрунтується робота різноманітних оптичних приладів. Далі розглянуто: 1.1. Основні поняття геометричної оптики 1.2. Закони відбивання і заломлення світла; повне відбивання |
1. Теоретичні відомості.
|
Далі розглянуто положення та закони, що визначають поширення світла в однорідних ізотропних середовищах і на межі поділу таких середовищ із різними властивостями: |
1.1. Основні поняття
Напрям поширення світла визначає промінь – лінія, вздовж якої світлова енергія від джерела приходить у дану точку. Промені уособлюють світлові пучки, який утворюються при проходженні світла від джерела крізь малі отвори (діафрагми). Але реально через дифракцію (див. п. 1.3) при проходженні крізь дуже малий отвір світловий пучок розходиться по різних напрямках, що обмежує застосовність законів геометричної оптики.
На межі поділу прозорих середовищ світловий потік частково відбивається і частково проходить (заломлюється) так, що в кожній точці падаючий, відбитий і заломлений промені лежать в одній площині падіння з нормаллю (перпендикуляром) до межі поділу середовищ. Кути між указаними променями та нормаллю (рис.16.1) теж мають відповідні назви:
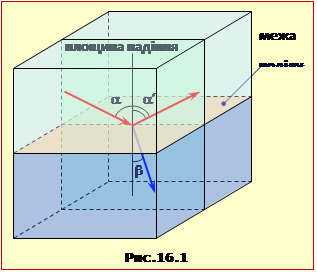 кут падіння (\(\alpha\)),
кут падіння (\(\alpha\)),
кут відбивання (\(\alpha^{\prime}\)),
кут заломлення (\(\beta\)).
1.2. Закони відбивання і заломлення
|
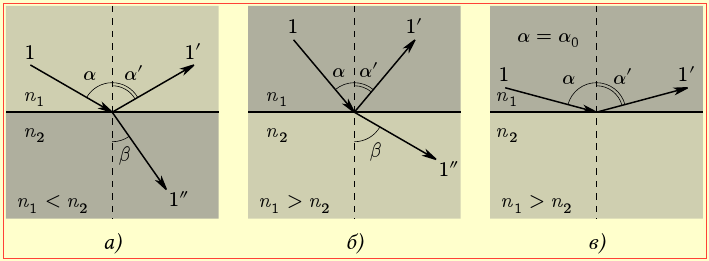
В однорідних ізотропних середовищах напрямки падаючого (1), відбитого (1′) і заломленого (1″) променів (рис. 16.2) пов'язані наступними законами. |
|
$\frac{\sin \alpha }{\sin \beta }=\frac{{{n}_{2}}}{{{n}_{1}}}$ або \(n_{1}\sin\alpha=n_{2}\sin\beta\) |
(1.3) |
Зауваження. В багатьох задачах на заломлення світла йдеться про візуальні спостереження. В такому разі, через малі розміри зіниці ока, слід використовувати наближення $\sin \alpha =\operatorname{tg}\alpha =\alpha $ і записувати закон заломлення у вигляді:
| \(\frac{\alpha}{\beta}=\frac{n_{2}} {n_{1}}\) або \(n_{1}\alpha=n_{2}\beta\). |
(1.3а) |
Із співвідношення (1.3) випливає, що при переході світла із оптично менш густого (n1 < n2) середовища в більш густе (рис.16.2а) заломлений промінь відхиляється в напрямку нормалі до межі поділу середовищ, а у випадку n1 > n2 (рис.16.2б) — від неї. В останньому випадку поступовому збільшенні кута падіння до деякій величині \(\alpha_{0}\) кут заломлення набуває максимально можливого значення \(90^{\circ}\) (рис.16.3). Відповідно, величина \(\alpha_{0}\) називається граничним кутом для даних двох середовищ і за законом (1.3), визначається співвідношенням
|
|
\(\sin\alpha_{0}=\frac{n_{2}}{n_{1}}\), \(n_{1}\gt{n}_{2}\). |
(1.4) |
Теорія й практика свідчать, що за вказаних умов при поступовому збільшенні кута падіння до величини \(\alpha_{0}\) інтенсивність заломленого променя зменшується до нуля, а відбитого променя збільшується від нуля до інтенсивності падаючого. Це означає, що при падінні з оптично більш густого середовища на межу з менш густи під кутом \(\alpha\ge\alpha_{0}\) світло далі не проходить, тобто відбувається повне внутрішнє відбивання. Прикладом цього, зокрема, є всім знайоме сліпуче виблискування на сонці дощових крапель на траві.
1.3. Дзеркала і лінзи
|
На законах геометричної оптики ґрунтується дія різних оптичних приладів, які ”озброюють“ око. Їхніми основними функціональними елементами є дзеркала та лінзи, котрі створюють зображення на екрані, чи безпосередньо на сітківці ока. Строга теорія зображень є складною. Тому в елементарній оптиці світлові промені, що потрапляють на дзеркало чи лінзу, по замовчуванню вважаються параксіальними (такими, що падають в околі центра і під малим кутом). |
Дія оптичних пристроїв (ОП) ґрунтується на тому, що промені, котрі виходять з однієї точки S (рис. 16.4), після проходження крізь пристрій самі (рис. 16.4а), або їхні продовження (рис. 16.4б), збираються теж в одній точці S′, яка є зображенням точки S.
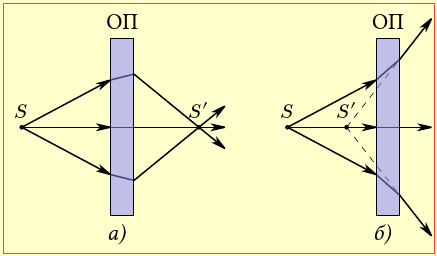
В першому випадку на поставленому в точці S′ екрані відбувається концентрація світлової енергії й утворюється дійсне зображення точки S. А в другому сходяться не самі промені, а їхні продовження, тож точка S′ є уявним зображенням точки S. Таке зображення можна побачити, пропустивши розбіжні промені, що пройшли, через додаткову збиральну лінзу, або, розглядаючи їх безпосередньо оком, кришталик якого править за додаткову лінзу, а сітківка – за екран.
Нагадаємо також, що створювані зображення, на загал, класифікують за такими ознаками:
- тип (дійсне чи уявне);
- розмір (збільшене або зменшене);
- орієнтація (пряме або перевернуте).
Далі розглядається утворення та характеристики зображень у найпростіших оптичних приладах, якими є плоскі та сферичні дзеркала й тонкі лінзи.
Плоске дзеркало. Це найпростіший оптичний прилад, що являє собою гладку плоску поверхню, котра повністю відбиває падаючі промені.
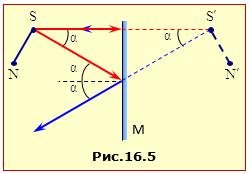
Рис. 16.5 ілюструє утворення зображення точки S і ”предмета“ SN у плоскому дзеркалі M. Ураховуючи закон відбивання (1.2) легко збагнути, що продовження відбитих дзеркалом променів, які вийшли з точки S, перетинаються в симетричній до неї точці \(S^{\prime}\). Те саме стосується й будь-якої іншої точки. Отже,
плоске дзеркало дає уявне пряме зображення предмета в натуральну величину,
котре відносно дзеркала є розташоване симетрично до самого предмета .
Сферичні дзеркала мають робочу поверхню у формі вгнутого, або опуклого сферичного сегмента (рис. 16.6) і характеризуються наступними геометричними параметрами:

- оптичний центр С – центр кривини робочої поверхні дзеркала;
- полюс O – вершина сферичного сегмента, що утворює дзеркало;
- головна оптична вісь CO – пряма, що проходить через центр і полюс дзеркала;
- побічна оптична вісь – будь-яка пряма, що проходить через оптичний центр дзеркала;
- фокус F – точка, в якій перетинаються відбиті промені у вгнутому та їхні продовження в опуклому дзеркалі при падінні паралельно до головної оптичній осі. Фокус знаходиться на головній оптичній осі й у вгнутому дзеркала є дійсний, а в опуклому – уявний.
- головна фокусна відстань F – відстань OF між полюсом і фокусом дзеркала – дорівнює половині радіуса кривини його поверхні:
|
|
\(F=\frac{R}{2}\) |
(1.5) |
- фокальна площина – площина, що проходить через фокус перпендикулярно до головної оптичної осі. Фокальна площина вгнутого дзеркала є дійсна, а опуклого – уявна.
Сферичне дзеркало є здатним до формування зображень, дякуючи наступній фокусувальній властивості:
|
будь-які паралельні між собою промені після відбивання від дзеркала самі, або їхні продовження перетинаються в одній точці фокальної площини. |
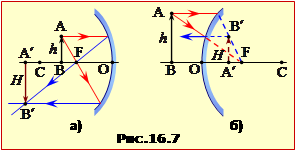
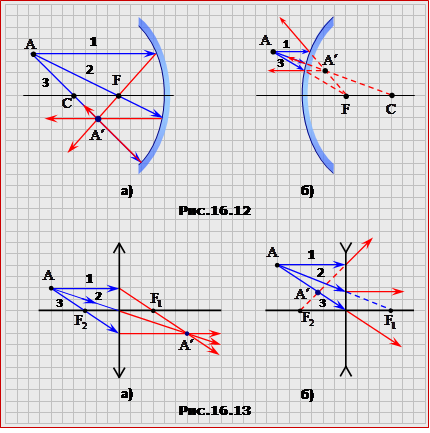
На рис. 16.7, відповідно до сказаного, наведено побудову зображення (стрілка A′B′) предмета (стрілка АВ) у вгнутому а) та опуклому б) дзеркалі, з якої можна встановити наступну формулу сферичного дзеркала:
|
|
\(\frac{1}{d}+\frac{1}{f}=\frac{1}{F}\), |
(1.6) |
де d = OA – відстань від предмета до дзеркала; f = OA′ – відстань від дзеркала до зображення; F = OF – головна фокусна відстань дзеркала. Ця формула охоплює всі можливі ситуації, якщо величини d, f, F розглядати як алгебраїчні у відповідності з наступним правилом знаків:
|
відстань між полюсом дзеркала і дійсною точкою береться зі знаком "+", а між полюсом і уявною точкою – зі знаком "–". |
(Нагадаємо, що в дійсних точках сходяться самі промені, а в уявних – їхні продовження).
Висота зображення H = A′B′ при заданій висоті предмета h = AB визначається поперечним збільшенням Г = (H/h), котре, як видно з рис. 16.7, складає
|
$\Gamma =\frac{f}{d}$. |
(1.7) |
Величина f задовольняє формулу (1.6), тож після елементарних перетворень отримаємо вираз
|
|
\(\Gamma=\frac{F}{d-F}\), |
(1.7а) |
в якому знак Г визначає тип зображення – при Г > 0 воно є дійсне, а при Г < 0 – уявне.
У вгнутому дзеркалі (F > 0) можливі різні випадки, а саме.
1. d > 2F : 0 < Г < 1 — зображення дійсне зменшене;
2. d = 2F : Г = 1 — зображення дійсне в натуральну величину;
3. F < d < 2F: Г > 1 — зображення дійсне збільшене;
4. d < F : Г < 1, — зображення уявне зменшене;
5. d = F: \(\Gamma\to\infty\) і, відповідно до формули (1.7), \(f\to\infty\). Це означає, що відбиті промені ніде не перетинаються, й зображення не існує.
Сферичні лінзи являють собою прозорі тіла з двома сферичними поверхнями. (Одна з поверхонь може бути й плоскою). На рис.16.8 показано в розрізі різні типи лінз: двоопукла (а), плоско-опукла (б), двовгнута (в), плоско-вгнута (г), опукло-вгнута, інакше меніск (д, е).
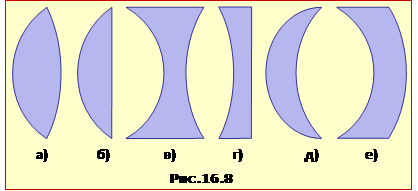
За дією на світлові пучки лінзи є подібні до дзеркал із тією відміною, що формують пучки не відбитих променів, а тих, що проходять крізь лінзу. Зокрема, лінзи теж поділяються на збиральні та розсіювальні. Перші перетворюють паралельний пучок променів на збіжний, а другі – на розбіжний. При цьому дія лінзи на хід променів визначається кривиною поверхонь і співвідношенням показників заломлення речовини лінзи та навколишнього середовища. До прикладу, у повітрі лінзи з профілем а), б), є збиральними, а типів в), г), – розсіювальними. Що до менісків, то їхня фокусувальна дія залежить від співвідношення кривин поверхонь, так на рис. 16.8 меніск д) є збиральним, а е) — розсіювальним.
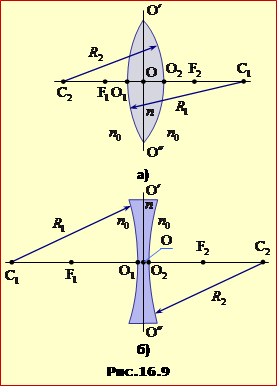 Для ілюстрації та кількісної характеристики впливу лінзи на світлові промені використовують наступні геометричні параметри (рис.16.9):
Для ілюстрації та кількісної характеристики впливу лінзи на світлові промені використовують наступні геометричні параметри (рис.16.9):
- радіуси кривини R1, R2 поверхонь;
- головна оптична вісь C1C2 – пряма, що проходить через центри кривини поверхонь;
- у тонкій лінзі можна вважати, що полюси O1 і O2 сферичних сегментів розташовані практично в одній точці O, що називається оптичним центром лінзи;
- побічна вісь – будь-яка пряма, що проходить через оптичний центр лінзи;
- площина лінзи O′O″ – площина, що проходить через оптичний центр лінзи перпендикулярно до головної оптичній осі;
- фокуси F1, F2 – точки на головній оптичній осі, у яких перетинаються заломлені промені (збиральна) або їхні продовження (розсіювальна лінза), котрі падають на лінзу паралельно до головної оптичної осі. У збиральній лінзі фокуси є дійсні, а в розсіювальній – уявні. Крім того можна вважати, що в тонкій лінзі фокуси розташовані на однаковій відстані від оптичного центра;
- фокусна відстань F = OF1 = OF2 – відстань між фокусом і оптичним центром лінзи;
- оптична сила лінзи D – величина, обернена до фокусній відстані:
|
|
\(D=\frac{1}{ F}\). |
(1.8) |
Оптична сила вимірюється в діоптріях (дптр): 1 дптр = 1 м–1 – це оптична сила лінзи з фокусною відстанню 1 м. Для збиральної лінзи оптична сила D > 0, для рзсювальної D < 0 і визначається формулою:.
|
|
\(D=\left(\frac{n}{n_{0}}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\). |
(1.9) |
де n, n0 – показники заломлення речовини лінзи та навколишнього середовища; R1, R2, – відповідно, радіуси кривини передньої та задньої відносно падаючого променя поверхні лінзи. При цьому величини R1, R2 розглядаються як алгебраїчні: радіус опуклої поверхні береться зі знаком "+", а вгнутої – зі знаком "–".
Зазвичай середовищем є повітря. В такому разі
|
\(D=\left({n}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\). |
(1.9а) |
- фокальна площина – площина, що проходить через фокус перпендикулярно до головної оптичної осі. Фокальна площина збиральної лінзи є дійсною, а розсіювальної – уявною й має наступну збиральну властивість:
|
будь–які паралельні між собою промені після проходження крізь лінзу перетинаються (самі або їхні продовження) в одній точці фокальної площини. |
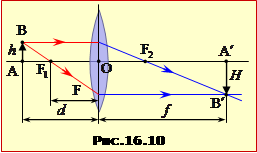
Розташування предмета AB та його зображення A′B′ у лінзі (рис. 16.10) є пов'язані формулою тонкої лінзи:
|
|
\(\frac{1}{d}+\frac{1}{f}=\frac{1}{F}\), |
(1.10) |
що по формі й суті збігається з формулою сферичного дзеркала (1.6) із таким самим правилом знаків.
Те саме стосується й формул поперечного збільшення:
|
|
\(\Gamma=\frac{f}{d}\), |
(1.11) |
|
|
\(\Gamma=\frac{F}{d-F}\). |
(1.11а) |
Формули (1.10), (1.11), (1.11а) та (1.6), (1.7) і (1.7a) є ідентичні. Це означає, що проведений для дзеркал аналіз зображень і встановлені співвідношення є чинними й для тонких лінз.
На завершення зауважимо, що на практиці в різних оптичних приладах часто використовують не поодинокі лінзи, а системи, з яких найпростішою є дві тонкі лінзи із спільною головною оптичною віссю. Зокрема, такою є око людини, "озброєне" окулярами.
Оптична сила системи лінз, розташованих впритул одна до одної, дорівнює алгебраїчній сумі оптичних сил з'єднаних лінз. Для двох лінз
|
|
D = D1 + D2. |
(1.12) |
1.4. Загальні рекомендації з розв'язування задач
Побудова зображень
Задачі цього типу вимагають копіткої роботи й передбачають наступні "правила гри":
- незалежно від кутів і відстаней на кресленнях, промені вважаються параксіальними (див. п. 1.3);
- аби відобразити на кресленні тип і тонкість лінзи, її зображують у вигляді відрізка із стрілками, або "вилками" на кінцях (рис.16.13) для збиральної та розсіювальної лінзи, відповідно;
- зображуваним предметом теж є стрілка (рис .16. 7, 16.10), отже побудова зображення полягає у графічному визначенні положення її кінців.
- при побудові зображення, предмета, що дотикається до головної оптичної осі лінзи (дзеркала) й розташований перпендикулярно, дозволено не будувати зображення точки дотику;
- при побудові зображення точки, що лежить на головній оптичній осі, заборонено додавати перпендикулярний допоміжний відрізок, зводячи задачу до визначення зображення точки, що не лежить на осі;
- побудова ходу променів виконується за допомогою тільки лінійки без використання шкали.
- усі промені, що виходять з однієї точки, після проходження через лінзу (дзеркало) самі, чи їхні продовження, теж перетинаються в одній точці. Тож для отримання зображення точки достатньо двох променів, що виходять з неї.
При розв'язуванні задач на побудову зображень корисно керуватись такими порадами.
|
1. |
Для побудови зображення А′ точки А без вимірювань (рис.16.12 (на б) поставити 2), рис.16.13(2 і 3 поміняти місцями)) слід користатися трьома "зручними" променями, хід яких є заздалегідь відомий, а саме, промінь 1, який іде паралельно до головної оптичної осі приладу; промінь 2, який проходить через фокус; промінь 3, який проходить через оптичний центр приладу.
|
|
|
|
|
2. |
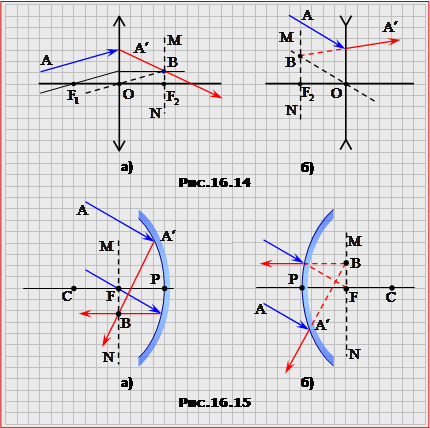
В деяких задачах за умовою можна використати тільки один з названих зручних променів (як, приміром, при побудові зображення точки, що лежить на головній оптичній осі (рис.16.11б). У такому разі за другий приймають довільний промінь і будують його хід, як показано на рис. 16.14 і рис.16.15.( перенести А′, як на 16.14)
Побудову слід виконувати в такій послідовності: а) показати фокальну площина MN; б) паралельно до заданого променя АА' провести один із ”зручних“ допоміжних променів і знайти точку його перетину В з фокальною площиною; в) через точки А' і В провести шуканий допоміжний промінь. |
|
|
|
|
3. |
Однією з типових задач на побудову є визначення розташування та характеристик лінзи за заданими положеннями якоїсь точки та її зображення. При цьому
|
|
|
|
Розрахункові задачі
А. Відбивання і заломлення світла. Розв'язуючи задачі такої тематики, варто пам'ятати наступне.
|
1) |
Коли світло падає на межу поділу з оптично більш густого середовища, то, перш ніж приступати до викладок, корисно знайти граничний кут і пересвідчитися, чи проходять промені крізь межу поділу середовищ, чи зазнають повного відбивання. |
|
|
|
|
2) |
Якщо за умовою кути падіння і заломлення малі (як це завжди є при візуальних спостереженнях), то при розв'язуванні задачі слід користуватися наближенням малих кутів \(\sin\alpha\approx\mathrm{tg}\alpha\approx\alpha\), і виражати їх у радіанах. Це значно спрощує викладки й обчислення, а інколи є й необхідною умовою отримання розв'язку. |
В. Формула дзеркала й лінзи. Формули дзеркала (1.6) і тонкої лінзи (1.10) є ідентичні. Тому в обох випадках задачі на визначення характеристик зображень розв'язуються за однаковою схемою. А саме, необхідно
|
1) |
На ескізному рисунку показати орієнтовні положення лінзи (дзеркала), предмета і його зображення без ходу променів та позначити відповідні відстані. (У найпростіших ситуаціях цього можна не робити). |
|
|
|
|
2) |
Скласти робочі рівняння: записати формулу лінзи (дзеркала) з урахуванням додаткових умов задачі, таких, як задана відстань між предметом та екраном, збільшення, тощо. При цьому слід ураховувати правило знаків, зокрема те, що фокусні відстані (або оптичні сили) вгнутого дзеркала і збиральної лінзи є завжди додатні, а опуклого дзеркала та розсіювальної лінзи – від'ємні. При цьому коли знак шуканої відстані не є очевидним, вона при викладках уважається додатньою. Істину покаже знак відповіді: "+" означатиме дійсну, а "–" уявну величину. |
|
|
|
|
3) |
У деяких задачах складання рівнянь і розв'язування задачі полегшується, якщо скористатись оборотністю світлових променів, яка полягає в тому, що предмет та його зображення можна міняти ролями. Це випливає із законів відбивання та заломлення світла. |
|
|
|
|
4) |
Розв'язати отримане рівняння (або систему рівнянь) і знайти аналітичну відповідь (формулу), яка показує положення, розміри та характер зображення. Відтак за допомогою лінійки виконати креслення з побудовою ходу променів. Це потрібно для ілюстрації та перевірки правильності відповіді. (До прикладу, чи часом не вийшло, що за розрахунками зображення є уявне, а хід променів засвідчує протилежне). |
2. Приклади розв’язування задач
Приклади розв'язування задач цього розділу поділені на теми:
2.1. Закони відбивання та заломлення
2.2. Побудова зображень у дзеркалах і лінзах
2.1. Закони відбивання і заломлення
Увага. Тут і далі по замовчуванню прийнято наступні умови:
– світлові пучки є параксіальні, тобто тонкі й не розбіжні;
– показники заломлення води й скла, відповідно, дорівнюють 1,33 і 1,5 .
Задача 2.1. Визначити кут відхилення \(\vartheta\) променя двогранним плоским дзеркалом із кутом між гранями \(\varphi\) при відбиванні в перпендикулярній до ребра площині.
Задача 2.2. Визначити, під яким кутом падає світло на межу поділу двох середовищ із відношенням показників заломлення k = 1,5, якщо відбитий та заломлений промені є взаємно перпендикулярні.
Задача 2.3. Спостерігач розглядає порожню непрозору кубічну посудину з кулькою на дні так, що повністю бачить стінку посудини, але не бачить дна (див. рис. 3 в розв'язку). Визначити, до якого найменшого рівня h слід наповнити посудину водою, аби спостерігач побачив кульку, якщо вона знаходиться на відстані S = 10 см від видимого краю дна.
Задача 2.4. На поверхні дотику двох пластин з показниками заломлення n1 = 1,35 i n2 = 1,95 та товщиною по h = 2 см зафарбовано круг радіусом r = h. Визначити радіус тіні R, яку відкидатиме круг на поверхню іншої пластини, якщо над його центром розмістити точкове джерело світла S на: А) першій пластині; В) другій пластині.
Задача 2.5. Промінь світла під кутом \(\alpha=60^{\circ}\) падає з повітря на скляну плоскопаралельну пластину товщиною d = 3 см. Визначити зміщення x променя внаслідок проходження пластини.
Задача 2.6. Пучок променів падає на аркуш паперу під кутом \(\alpha=60^{\circ}\). Визначити, на яку відстань S зміститься світна цятка на папері, якщо на нього покласти скляну пластину товщиною d = 5 см.
Задача 2.7. Рибалці в човні, котрий прямо під собою розглядає камінець на дні ставка, здається, що він знаходиться на глибині h = 3 м. Визначити справжню глибину ставка H.
Задача 2.8. Промінь, який падає на трикутну призму під кутом \(\alpha=30^{\circ}\) і виходить під кутом \(\beta=60^{\circ}\), відхиляється на кут \(\delta=45^{\circ}\). Визначити заломний кут призми \(\varphi\).
Задача 2.9. Промінь світла під малим кутом падає на бічну грань скляної призми із заломним кутом \(\varphi=0,1\) рад. Визначити кут відхилення \(\delta\) променя призмою.
Задача 2.10. Промінь світла падає на бічну грань скляної призми із заломним кутом \(\varphi=60^{\circ}\) і непрозорою основою. Визначити мінімальне значення кута падіння \(\alpha_{m}\), при якому світло проходитиме крізь призму.
Задача 2.1
Визначити
кут відхилення \(\vartheta\) променя двогранним плоским дзеркалом із кутом між гранями \(\varphi\) при відбиванні в перпендикулярній до ребра площині.
|
Дано: \(\varphi\)
|
|
\(\vartheta\) - ?
|
Розв’язання
На рис. 1 з урахуванням закону відбивання (2.2) показано хід променя, що падає й відбивається на першій грані дзеркала під якимось кутом \(\alpha_{1}\), а на другій – під відповідним кутом \(\alpha_{2}\), та шуканий кут відхилення \(\vartheta\), тобто кут між напрямами променя, що падає на першу грань дзеркала, та того, що відбивається від другої.
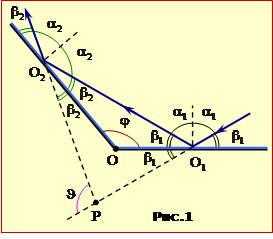
Показані також усі інші кути, що потрібні для розв’язування задачі.
Із рис. 1 видно, що кут відхилення \(\vartheta\) є зовнішнім кутом трикутника PO1O2, отже
\(\vartheta=2\beta_{1}+2\beta_{2}=2(\beta_{1}+\beta_{2})\).
А з трикутника O1OO2 маємо
\(\beta_{1}+\beta_{2}=180^{\circ}-\varphi\),
Отже шуканий кут відхилення
\(\vartheta=360^{\circ}-2\varphi\).
В отриманій відповіді заслуговує на увагу те, що цей кут не залежить від напрямку падаючого променя й визначається тільки величиною двогранного кута \(varphi\). Зокрема, якщо \(\varphi=90^{\circ}\), то \(\vartheta=180^{\circ}\). Тобто, прямокутне двогранне дзеркало будь-які промені, що падають у перпендикулярній до його ребра площині, відбиває у зворотньому напрямі. А тригранне прямокутне дзеркало, як можна довести, має таку властивість узагалі незалежно від напрямку падаючих променів. Це використовується у так званих кутових відбивачах, якими, зокрема, є катафоти автомобілів і велосипедів, а також рефлектори на ранцях школярів.
Задача 2.2
Визначити,
під яким кутом \(\alpha\) падає світло на межу поділу двох середовищ із відношенням показників заломлення k = 1,5, якщо відбитий та заломлений промені є взаємно перпендикулярні.
|
Дано: k = 1,5
\(\varphi=90^{\circ}\)
|
|
\(\alpha\) - ?
|
Розв’язання
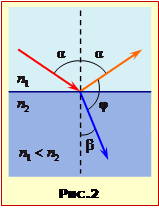 Із рис. 2, на якому показано хід довільного променя при падінні світла на межу поділу з оптично менш густого середовища (n1 < n2), видно, що \(\alpha+\varphi+\beta=180^{\circ}\). Отже, при \(\varphi=90^{\circ}\) кут заломлення \(\beta=90^{\circ}-\alpha\), і $\sin \beta =\cos \alpha $. Тож за заоном заломлення (2.3)
Із рис. 2, на якому показано хід довільного променя при падінні світла на межу поділу з оптично менш густого середовища (n1 < n2), видно, що \(\alpha+\varphi+\beta=180^{\circ}\). Отже, при \(\varphi=90^{\circ}\) кут заломлення \(\beta=90^{\circ}-\alpha\), і $\sin \beta =\cos \alpha $. Тож за заоном заломлення (2.3)
Числова відповідь залежить послідовності проходження світлом середовищ, тож є два випадки:
|
1) \(\frac{n_{2}}{n_{1}}=k\) і \(\alpha_{1}=\mathrm{arctg}{1,5}=56,3^{\circ}\); |
|
2) \(\frac{n_{2}}{n_{1}}=\frac{1}{k}\) і \(\alpha_{2}=\mathrm{arctg}\frac{1}{1,5}=33,7^{\circ}\). |
Корисно звернути увагу на те, що одне з цих значень є кутом падіння, а інше – кутом заломлення, незалежно від послідовності проходження світлом середовищ.
Задача 2.3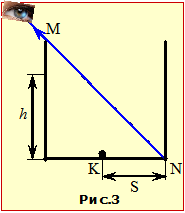
Спостерігач розглядає порожню непрозору кубічну посудину з кулькою на дні так, що повністюбачить стінку посудини, але не бачить дна (рис. 3).
Визначити,
до якого найменшого рівня h слід наповнити посудину водою, аби спостерігач побачив кульку, якщо вона знаходиться на відстані S = 10 см від видимого краю дна .
|
Дано: n = 1,33
S = 10 см
|
|
h - ?
|
Розв’язання
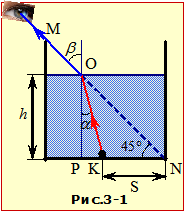 З умови випливає, що, аби спостерігач бачив кульку, відбите нею світло має заломлюватися на поверхні води під заданим кутом β = 45° (див. рис 3-1) і падати на неї під відповідним кутом α, що за законом заломлення (2.3) задовольняє умову:
З умови випливає, що, аби спостерігач бачив кульку, відбите нею світло має заломлюватися на поверхні води під заданим кутом β = 45° (див. рис 3-1) і падати на неї під відповідним кутом α, що за законом заломлення (2.3) задовольняє умову:
| \(\sin\alpha=\frac{1}{n\sqrt{2}}\). |
(1) |
Отже, при заданому положенні кульки величина α по суті теж є відомою. Це дозволяє визначити потрібну висоту рівня води h з рис. 3-1, на якому довжина відрізка KN = S, враховуючи кут зору, PN = h, і
| PK = h – S. |
|
У той же час
|
PK = htg\(\alpha\), |
тож, прирівнявши праві частини наведених виразів, отримаємо:
$h=\frac{S}{1-\operatorname{tg}\alpha }$
Відтак, виразивши тангенс через синус і врахувавши значення (1), після нескладних викладок дістанемо відповідь:
$h=\frac{S}{1-\sqrt{2{{n}^{2}}-1}}$ \(=26,9\) см.
В отриманій відповіді може здивувати, що потрібна висота рівня води не залежить від розмірів посудини. Але це пояснюєься кубічною формою посудини, через що при змінїї її розмірів кут зору, тож і кут падіння променя на поверхню води, не змінюються.Задача 2.4
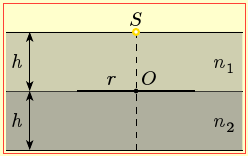
На поверхні дотику двох пластин з показниками заломлення n1 = 1,35 i n2 = 1,95 і товщиною по h = 2 см зафарбовано круг радіусом r = h.
Визначити
радіус тіні R, яку відкидатиме круг на поверхню іншої пластини, якщо над його центром розмістити точкове джерело світла S на:
А) першій пластині;
В) другій пластині.
|
Дано: h = 2 см
\(n_{1}\) = 1,35
\(n_{2}\) = 1,95
|
|
R - ?
|
Розв’язання
А) У цьому випадку світло переходить з оптично менш густого середовища в більш густе, й заломлюється,як показано на рис. 4-1а. За законом заломлення (1.3) радіус тіні
\(R=r+h\mathrm{tg}\beta\).
При цьому за умовою r = h,
$R=h(1+\operatorname{tg}\beta )$,
тож, виразивши тангенс через синус, як
$\operatorname{tg}\beta =\frac{\sin \beta }{\sqrt{1-{{\sin }^{2}}\beta }}=\frac{1}{\sqrt{\left( 1/{{\sin }^{2}}\beta \right)-1}}$,
дістанемо
$R=\left( 1+\frac{1}{\sqrt{\left( 1/{{\sin }^{2}}\beta \right)-1}} \right)$.
За умовою α = 45°, отже величина \(1/\sin^{2}\beta\) за законом заломлення (2.4) складає
\(\frac{1}{\sin^{2}\beta}=\frac{2n_{2}^{2}}{n_{1}^{2}}\),
і шуканий радіус тіні
\(R=h\left(1+\frac{1}{\sqrt{2(n_{2}/n_{1})^{2}-1}}\right)\approx3,1\) см.
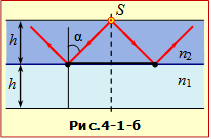 Б) В цьому випадку світло падає на межу поділу з більш густого середовища, тому, перш ніж виконувати обчислення, слід з'ясувати, чи зможе світло взагалі пройти через межу поділу. Для цього за допомогою формули (1.4) знаходимо граничний кут для заданих речовин речовин:
Б) В цьому випадку світло падає на межу поділу з більш густого середовища, тому, перш ніж виконувати обчислення, слід з'ясувати, чи зможе світло взагалі пройти через межу поділу. Для цього за допомогою формули (1.4) знаходимо граничний кут для заданих речовин речовин:
\(\alpha_{0}=\mathrm{arcsin}\left(\frac{n_{1}}{n_{2}}\right)=43,8^{\circ}\).
Так що кут падіння (\(45^{\circ}\))крізь межу дотику пластин не пройде жоден промінь (див. п. 2.2), і вся вона буде затінена. Тож формально відповідь записується як
\(R\to\infty\).
Задача 2.5
Промінь світла під кутом \(\alpha=60^{\circ}\) падає з повітря на скляну плоскопаралельну пластину товщиною d = 3 см.|
Дано: \(\alpha\) = \(60^{\circ}\)
n = 1,5
d = 3 см
|
|
x - ?
|
Розв’язання
На рис. 5-1 із необхідними позначеннями показано хід променя крізь плоскопаралельну пластинку. Тож на основі закону заломлення світла (1.3) для верхньої та нижньої граней можна записати:
\(\frac{\sin\alpha}{\sin\beta}=n\), \(\frac{\sin\beta}{\sin\alpha^{\prime}}=\frac{1}{n}\).
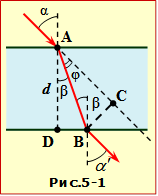
З цих виразів випливає, що \(\alpha^{\prime}=\alpha\), тобто промінь, не змінюючи напрякму, зміщується на певну відстань x = BC, яку треба визначити.
Для отримання відповіді скористаємося рисунком 5.1, на якому трикутник ΔАВС є прямокутним із гіпотенузою АВ = (d/cosβ). тож
$x=AB·sinφ =\frac{d\sin \varphi }{\cos \beta }$,
де
$\varphi =\alpha -\beta $.
Далі, скориставшся формулою синуса різниці кутів, дістанемо:
$x=\frac{d\sin \left( \alpha -\beta \right)}{\cos \alpha }$ = $d\frac{\sin \alpha \cos \beta -\cos \alpha \sin \beta }{\cos \beta }$ =
= $d\left( \sin \alpha -\cos \alpha \operatorname{tg}\beta \right)$
У цьому виразі кут $\beta$ задовольняє закон заломлення світла. Тож, виразивши $\operatorname{tg}\beta $ через $\sin \beta $, відповідно до закону заломлення (1.3), отримаємо остаточну відповідь:
$x=d\sin \alpha \left( 1-\frac{\cos \alpha }{\sqrt{{{n}^{2}}-{{\sin }^{2}}\alpha }} \right)$ =\(1,53\) см.
Задача 2.6
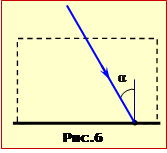 Вузький паралельний пучок променів падає на аркуш паперу під кутом \(\alpha=60^{\circ}\) і створює світлову пляму (рис. 6).
Вузький паралельний пучок променів падає на аркуш паперу під кутом \(\alpha=60^{\circ}\) і створює світлову пляму (рис. 6).
Визначити
відстань S на яку зміститься цятка, якщо на папір покласти скляну (n = 1,5) пластину товщиною d = 5 см.
|
Дано: α = 60°
n = 1,5
d = 5 см
|
|
S - ?
|
Розв’язання
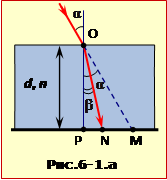 Нехай спочатку світна цятка розміщена в точці M (рис. 6-1.а). Після того як на папір поклали пластину, цятка внаслідок заломлення переміститься в точку N.
Нехай спочатку світна цятка розміщена в точці M (рис. 6-1.а). Після того як на папір поклали пластину, цятка внаслідок заломлення переміститься в точку N.
Шукана відстань S = MN. З рисунка видно, що
|
|
S = PM – PN = \(d(\mathrm{tg}\alpha-\mathrm{tg}\beta)\). |
(1) |
Величину \(\mathrm{tg}\beta\) легко визначити через відомі тригонометричні співвідношення та закон заломлення (1.3), згідно з яким \(\sin\beta=\sin\alpha/n\)
\(d(\mathrm{tg}\beta=\frac{\sin\beta}{\cos\beta}=\frac{\sin\beta}{\sqrt{1-\sin^{2}\beta}}=\frac{\sin\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\).
Підставивши цей вираз у формулу (1), дістанемо відповідь:
\(S=d\left(\mathrm{tg}\alpha-\frac{\sin\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)\).
Обчислення дають:
\(S=5\cdot\left(\sqrt{3}-\frac{\sqrt{3}}{2\cdot\sqrt{1,5^{2}-3/4}}\right)\approx\) 5,1 см.
Одержати відповідь у цій задачі також можна інакше.
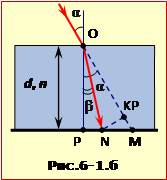 Дійсно, якщо з точки N опустити перпендикуляр на лінію OM (рис. 16-2.б), то з трикутника NKM: NM = NK/\(\cos\alpha\). Відрізок NK = x був визначений у задачі 2.5 формула (4).
Дійсно, якщо з точки N опустити перпендикуляр на лінію OM (рис. 16-2.б), то з трикутника NKM: NM = NK/\(\cos\alpha\). Відрізок NK = x був визначений у задачі 2.5 формула (4).
Отже маємо:
\(S=d\mathrm{tg}\alpha\left(1-\frac{\cos\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)=d\left(\mathrm{tg}\alpha-\frac{\sin\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)\).
Задача 2.7.
Рибалці в човні, котрий прямо під собою розглядає камінець на дні ставка, здається, що він знаходиться на глибині 3 м.
Визначити
справжню глибину ставка H.
|
Дано: h= 3 м
n = 1,33
|
|
H - ?
|
Розв’язання
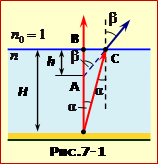 Відповідно до закону заломлення світла (2.3), відбиті від камінця промені світла на виході з води заломлюються під більшим кутом, аніж падають, як показано на рис. 7-2. Тому при потраплянні в око рибалки вони створюють хибне враження, що камінець знаходиться в т. А на глибині h, меншій ніж справжня глибина H. При цьому, як зрозуміло з рисунка,
Відповідно до закону заломлення світла (2.3), відбиті від камінця промені світла на виході з води заломлюються під більшим кутом, аніж падають, як показано на рис. 7-2. Тому при потраплянні в око рибалки вони створюють хибне враження, що камінець знаходиться в т. А на глибині h, меншій ніж справжня глибина H. При цьому, як зрозуміло з рисунка,
$\frac{H}{h}=\frac{\operatorname{tg}\beta }{\operatorname{tg}\alpha }$
або, беручи до уваги малість кутів,
$\frac{H}{h}=\frac{\beta }{\alpha }$ $\Rightarrow $ $H=h\frac{\beta }{\alpha }$
де відношення кутів, згідно із законом заломлення (1.3а), дорівнює відношенню показників заломлення води n та повітря n0 = 2. Отже, справжня глибина ставка
\(H=nh=4\) м.
Задача 2.8
Промінь, який падає на призму під кутом \(\alpha=30^{\circ}\) і виходить під кутом \(\beta=60^{\circ}\), відхиляється на кут \(\delta=45^{\circ}\).
Визначити
заломний кут призми \(\varphi\).
|
Дано: α1 = 30°
α2 = 60°
δ = 45°
|
|
φ - ?
|
Розв’язання
Позначимо кут заломлення на першій грані \(\beta_{1}\), а кут падіння на другу грань \(\beta_{2}\) (рис.8-1).
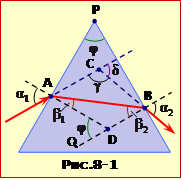 Кут відхилення променя \(\delta\) – то є кут між напрямками променя, що вийшов з призми та променя, що падає на призму. Він є зовнішнім кутом трикутника ΔABC, отже
Кут відхилення променя \(\delta\) – то є кут між напрямками променя, що вийшов з призми та променя, що падає на призму. Він є зовнішнім кутом трикутника ΔABC, отже
|
|
\(\delta=\pi-\gamma\) \(\Rightarrow\) \(\gamma=\pi-\delta\). |
(1) |
В цьому трикутнику \(\angle\)BAC = \(\alpha_{1}-\beta_{1}\) і \(\angle\)ABC = \(\alpha_{2}-\beta_{2}\). Тому
|
|
\(\gamma=\pi-(\alpha_{1}-\beta_{1})-(\alpha_{2}-\beta_{2})=\pi-(\alpha_{1}+\alpha_{2})+(\beta_{1}+\beta_{2})\). |
(2) |
Прирівнюючи праві частини виразів (1) і (2), отримаємо:
|
|
\(\delta=(\alpha_{1}+\alpha_{2})-(\beta_{1}+\beta_{2})\). |
(3) |
Зовнішній кут \(\angle\)ADQ трикутника ABD дорівнює заломному кутові призми \(\varphi\), оскільки він утворений перпендикулярами до бічних граней призми. Отже
|
|
\(\varphi=\beta{1}+\beta_{2}\). |
(4) |
Підставивши цей вираз у формулу (3), дістанемо відповідь:
\(\delta=\alpha_{1}+\alpha_{2}-\varphi\) \(\Rightarrow\) \(\varphi=\alpha_{1}+\alpha_{2}-\delta=30^{\circ}+60^{\circ}-45^{\circ}\)
Задача 2.9
Промінь світла під малим кутом падає на бічну грань скляної призми із заломним кутом \(\varphi=0,1\) рад.кут відхилення \(\delta\) променя призмою.
|
Дано: φ = 0,1 рад
n = 1,5
|
|
δ - ?
|
Розв’язання
Скористаємося результатами задачі 2.8 (формули (3) і (4)):
|
|
\(\delta=(\alpha_{1}+\alpha_{2})-(\beta_{1}+\beta_{2})\); |
(1) |
|
|
\(\varphi=\beta_{1}+\beta_{2}\). |
(2) |
Відтак залишається визначити суму кутів \(\alpha_{1}\) та \(\alpha_{2}\). При малих кутах \(\sin\alpha\approx\alpha\), отже, за законом заломлення (1.3) можна наближено записати
|
|
\(\frac{\alpha_{1}}{\beta_{1}}=n\) \(\Rightarrow\) \(\alpha_{1}=n\beta_{1}\), \(\frac{\beta_{2}}{\alpha_{2}}=\frac{1}{n}\) \(\Rightarrow\) \(\alpha_{2}=n\beta_{2}\). |
(3) |
де n – показник заломлення призми. Підставивши вирази (3) у формулу (1) і врахувавши співвідношення, (2) отримаємо:
\(\delta=n(\beta_{1}+\beta_{2})-(\beta_{1}+\beta_{2})=(n-1)\varphi\).
Таким чином, при малих кутах падіння кут відхилення променя в призмі з малим заломним кутом залежить тільки від показника заломлення та заломного кута.
Виконаємо обчислення:
\(\delta=(1,5-1)\cdot{0,1}=0,05\) рад = \(2,86^{\circ}\).
Задача 2.10
Промінь світла падає на бічну грань скляної призми із заломним кутом \(\varphi=60^{\circ}\) і непрозорою основою. Визначити мінімальне значення кута падіння \(\alpha_{m}\), при якому світло проходитиме крізь призму.
|
Дано: n = 1,5
φ = 60°
|
|
αm - ?
|
Розв’язання
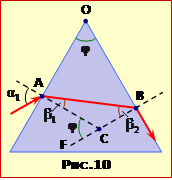 На рис.10 показаний хід граничного променя крізь призму і відповідні кути.
На рис.10 показаний хід граничного променя крізь призму і відповідні кути.
Світло буде проходити крізь призму за умови
|
\(\beta_{2}\le\beta_{г}\), |
(1) |
де \(\beta_{г}\) – граничний кут, для якого відповідно до формули (2.7), умову (1) можна записати, як
\(\sin\beta_{2}\le\frac{1}{n}\).
З іншого боку (див. задачу 2.8, формула (4))
|
|
\(\varphi=\beta_{1}+\beta_{2}\) \(\Rightarrow\) \(\beta_{2}=\varphi-\beta_{1}\). |
(2) |
відповідно до цього світло проходить крізь призму за умови
\(\sin(\varphi-\beta_{1})\le\frac{1}{n}\).
З виразів (1) і (2) слідує, що найбільшій величині \(\beta_{1}=\beta_{г}\) відповідає таке значення \(\beta_{1}=\beta_{m}\), при якому
|
|
\(\sin(\varphi-\beta_{m})=\frac{1}{n}\). |
(3) |
За законом заломлення (1.3) найменшому значенню \(\beta_{1}=\beta_{m}\) відповідає шуканий найменший кут падіння \(\alpha_{1}=\alpha_{m}\), причому
\(\sin\beta_{m}=\frac{\sin\alpha_{m}}{n}\).
Підставляючи цей вираз в рівність (3) і використовуючи відому тригонометричну формулу, одержимо
\(\frac{1}{n}=\sin\varphi\cdot\frac{1}{n}\sqrt{n^{2}-\sin^{2}\alpha_{m}}-\frac{1}{n}\sin\alpha_{m}\cos\varphi\) \(\Rightarrow\)
\(\Rightarrow\) \(1+\sin\alpha_{m}\cos\varphi=\sin\varphi\sqrt{n^{2}-\sin^{2}\alpha_{m}}\).
Зведемо останній вираз в квадрат і виконаємо перетворення:
\(\sin^{2}\alpha_{m}+2\sin\alpha_{m}\cos\varphi+1-n^{2}\sin^{2}\varphi=0\).
Рішення цього квадратного рівняння відносно \(\sin\alpha_{m}\) дає
\(\sin\alpha_{m}=-\cos\varphi+\sqrt{\cos^{2}\varphi-1+n^{2}\sin\varphi}=-\cos\varphi+\sin\varphi\sqrt{n^{2}-1}\).
(Другий корінь не має фізичного змісту).
Виконаємо обчислення:
\(\sin\alpha{m}=-\cos{60^{\circ}}+\sin{60^{\circ}}\sqrt{1,5^{2}-1}\) \(\Rightarrow\) \(\alpha_{m}=27,9^{\circ}\).
2.2. Побудова зображень у дзеркалах і лінзах
Наступні приклади, відповідно до наведених загальних рекомендацій (п. 1.4), ілюструють порядок побудови зображення предмета та ходу заданого променя в дзеркалах і лінзах. ”Предметом“ по замовчуванню є стрілка АВ, яка по замовчуванню спрямована перпендикулярно до горизонтальної головної оптичної осі дзеркала чи лінзи й спирається на неї. Тому для побудови зображення ”предмета“ достатньо визначати положення тільки верхнього кінця стрілки.
Задача 2.11. Побудувати та дати характеристику зображення предмета, що розташований між фокусом F і полюсом P вгнутого сферичного дзеркала.
Задача 2.12. За заданим ходом променя крізь збиральну лінзу визначити положення її фокусів.
Задача 2.13. Визначити хід променя 2 після заломлення в розсіювальній лінзі за заданим ходом променя 1.
Задача 2.14. Побудувати та дати характеристику зображення предмета, котрий похило розташовано між фокусом F і подвійним фокусом 2F збиральної лінзи.
Задача 2.15. За заданим положенням точки S і її зображення S′ відносно головної оптичної осі O′O″ лінзи визначити її тип та положення оптичного центра й фокусів.
Задача 2.11
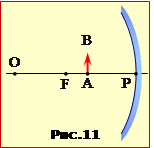 Побудувати та дати характеристику зображення предмета АВ, що розташований між фокусом F і полюсом P вгнутого сферичного дзеркала, рис. 11.
Побудувати та дати характеристику зображення предмета АВ, що розташований між фокусом F і полюсом P вгнутого сферичного дзеркала, рис. 11.
Побудувати
зображення \(\mathrm{A^{\prime}B^{\prime}}\) предмета.
Розв’язання
Згідно з прийнятими домовленостями, для отримання відповіді треба побудувати зображення точки B. Будемо робити це в такій послідовності:
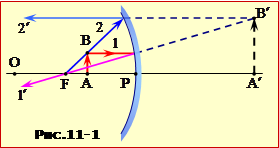 1. Із точки B паралельно до головної оптичній осі OP проведемо падаючий промінь 1 і відбитий промінь 1′, що проходить через фокус дзеркала F;
1. Із точки B паралельно до головної оптичній осі OP проведемо падаючий промінь 1 і відбитий промінь 1′, що проходить через фокус дзеркала F;
2. Із фокуса F через точку B спрямуємо на дзеркало промінь 2 і паралельно до осі OP відбитий промінь 2′;
3. Продовживши промені 1′ і 2′ до перетину, знаходимо положення B′ уявного зображення точки B;
4. Опускаємо з точки B′ перпендикуляр на головну оптичну вісь дзеркала OP і визначаємо положення A′ зображення точки A , тож і предмета (стрілка A′B′).
Отже, при розташовані предмета між полюсом і фокусом вгнуте дзеркало дає його уявне, пряме і збільшене зображення. (Завдяки цьому, вгнуті дзеркала використовуються чоловіками при голінні).
Задача 2.12
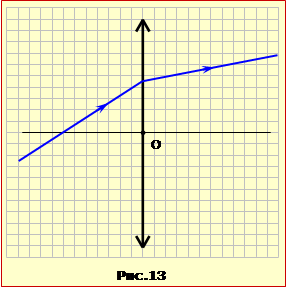
За заданим ходом променя крізь збиральну лінзу (рис. 13)
визначити
положення її фокусів.
Розв’язання
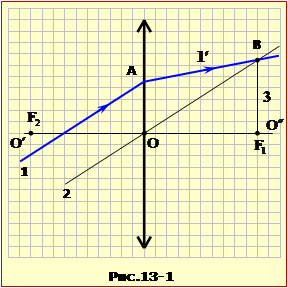
Відомо (див. п. 1.3), що будь-які паралельні промені після заломлення в лінзі перетинаються в одній точці фокальної площини. Тож, якщо через оптичний центр лінзи О паралельно до падаючого променя 1 провести допоміжний промінь 2 (рис. 13-1), то на його перетині із заломленим променем 1′ отримаємо точку В, яка лежить у фокальній площині лінзи. Відтак, опустивши перпендикуляр на вісь О′О″, знайдемо положення фокуса F1 і симетрично по інший бік – F2.
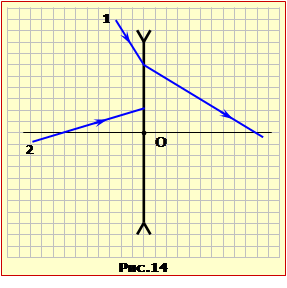
Задача 2.13
 Визначити
Визначити
хід променя 2 після заломлення в розсівній лінзі за заданим ходом променя 1 (рис. 14).
Розв’язання
Побудова ходу променя 2, яку ілюструє рис. 14-1, виконуємо в такій послідовності.
1. Як у попередній задачі, паралельно до променя 1 проводимо побічну оптичну вісь (”допоміжний промінь“), і на її перетині з продовженням променя 1′ дістаємо точку С, яка визначає положення фокальної площини, тож і фокуса F лінзи;
2. Так само проводимо другу побічну оптичну вісь паралельно до променя 2 і відмічаємо точку D її перетину з фокальною площиною;
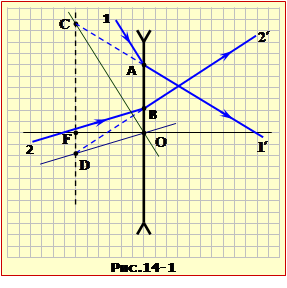 3. Оскільки через точку D проходить і продовження шуканого заломленого променя 2′, його напрям DB є такий, як показано на рисунку.
3. Оскільки через точку D проходить і продовження шуканого заломленого променя 2′, його напрям DB є такий, як показано на рисунку.
Задача 2.14
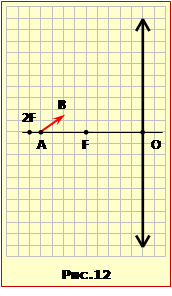 Побудувати та дати характеристику
Побудувати та дати характеристику
зображення предмета, котрий похило розташовано між фокусом F і подвійним фокусом 2F збиральної лінзи (рис. 12).
Розв’язання
Задача полягає в побудові зображення А′ і В′ кінців стрілки АВ, яку ілюструє рис. 12-1.
Точка A′. Для побудови використаємо промені: 1, який збігається з головною оптичною віссю, і 2, що є спрямований уздовж відрізка AB. Далі паралельно до АВ проведемо побічну оптичну вісь ОD, яка перетинає фокальну площину лінзи в точці D. І, позаяк через цю точку проходить і заломлений промінь 2′, на його перетині з променем 1′ (головна оптична вісь) дістанемо зображення А′ нижнього кінця стрілки АВ.
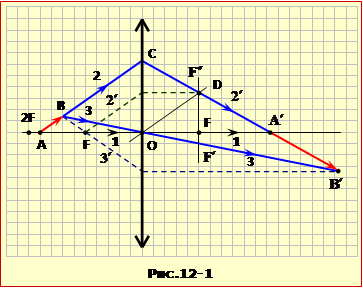
Точка B′. Для побудови зображення верхнього кінця стрілки теж треба визначити хід крізь лінзу двох променів, що виходять з точки B. Тож у якості одного зручно взяти використаний вище промінь 2. Далі без заломлення проведемо через оптичний центр лінзи промінь 3 і на його перетині з продовженням променя 2′ отримаємо зображення верхнього кінця B′, тож і всієї стрілки A′B′. Як видно, воно воно є дійсне, збільшене і перевернуте.
Зауваження. При побудові можна було би взяти й інші промені, приміром ті, що показано на рисунку штриховими лініями прибрати позначення.
Задача 2.15
За заданим положенням точки S і її зображення S′ відносно головної оптичної осі лінзи О′О″ 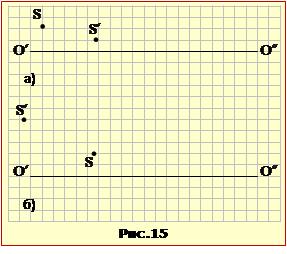 (рис. 15а,б)
(рис. 15а,б)
Визначити
її тип і положення оптичного центра та фокусів.
Розв’язання
Ключем до розв’язування задачі є той факт, що точка та її зображення лежать на одній прямій, що проходить через оптичний центр лінзи (див. п. 1.4).
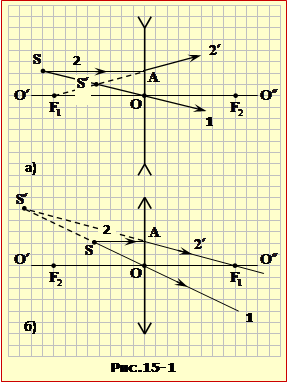
Побудову виконаємо паралельно для обох випадків у наступній послідовності (рис. 15-1а для розсіювальної й 15-1,б для збиральної лінзи).
1. Проводимо промінь 1 через точки S і S′ і на його перетині з оптичною віссю O′O″ одержуємо положення оптичного центра O та площини лінзи.
2. Із точки S на лінзу паралельно до O′O″ (в точку A) напрямляємо промінь 2, який після заломлення (сам чи його продовження) має проходити через точку S′ – зображення S.
3. Відтак на перетині променя 2′ або його продовження з віссю O′O″ знаходимо положення одного і симетрично по інший бік – другого фокуса лінзи.
Отож, як видно з виконаної побудови, у випадку а) лінза є розсіювальною, а у випадку б) – збиральною.
2.3. Формули дзеркала і лінзи
Задача 2.16. Рефлектор прожектора являє собою вгнуте сферичне дзеркало з радіусом кривини R = 30 см. Визначити на якій відстані l від його фокуса на головній оптичній осі слід розмістити точкове джерело світла, аби одержати конічний пучок променів із точкою сходження на відстані L = 10 м від полюса.
Задача 2.17. Промені збіжного конічного пучка, що проходять крізь розсіювальну лінзу з фокусною відстанню F = 30 см, перетинаються на головній оптичній осі на відстані L = 60 см від лінзи. Визначити, на яку відстань l зміститься точка сходження променів, якщо лінзу прибрати.
Задача 2.18. Мураха повзе вздовж головної оптичної осі опуклого дзеркала із фокусною відстанню F зі швидкістю v = 5 мм/с. Побудувати зображення мурахи та визначити швидкість його руху u на момент знаходження мурахи на відстані d = 1,5F від дзеркала.
Задача 2.19. Малий предмет розглядають крізь лупу із фокусною відстанню F = 5 см так, що зображення утворюється на відстані найкращого зору L = 25 см. Визначити, на якій відстані d від предмета розташовано лупу, та яке збільшення \(\Gamma\) вона дає.
Задача 2.20. Визначити: а) при якій відстані d0 від предмета до лінзи з фокусною відстанню F відстань L між ним і його зображенням на екрані буде мінімальною та б) її величину L0.
Задача 2.21. Лінза дає чітке зображення джерела світла на екрані в двох положеннях на відстані l = 60 см одне від одного. Визначити фокусну відстань лінзи F, якщо відстань від неї до екрана L = 1 м.
Задача 2.22. Короткозора людина читає книжку, тримаючи її на відстані d = 16 см від очей, тоді як відстань найкращого зору складає d0 = 25 см. Визначити оптичну силу Dc окулярів, які їй потрібні для корекції зору.
Задача 2.23. На одній осі зі збиральною лінзою Л1 із заданою фокусною відстанню F1 встановлено розсіювальну лінзу Л2. Визначити її фокусну відстань F2, якщо система створює збільшене в \(\Gamma=2\) рази дійсне зображення предмета, котрий розміщено перед збиральною лінзою на відстані d1 = 3F1.
Задача 2.16
Рефлектор прожектора являє собою вгнуте сферичне дзеркало з радіусом кривини R = 30 см.
Визначити,
на якій відстані l від фокуса дзеркала на головній оптичній осі слід розмістити точкове джерело світла, аби одержати конічний пучок променів із точкою сходження на відстані L = 10 м від полюса.
|
Дано: R = 30 см = 0,3 м
L = 10 м
|
|
l - ?
|
Розв’язання
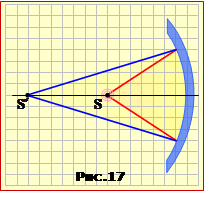 Положення джерела S і точки сходження S′ відбитого пучка схематично (без дотримання співвідношеь між відстанями) показані на рис. 17, з якого зрозуміло, що точка S′ є дійсним зображенням джерела S (див. п.1.3), котре є віддалене від полюса дзеркала на відстань f = L, а відстань d від самого джерела S до полюса перевищує фокусну відстань F на шукану величину l: d = F + l. Отже, згідно з формулою дзеркала (1.6),
Положення джерела S і точки сходження S′ відбитого пучка схематично (без дотримання співвідношеь між відстанями) показані на рис. 17, з якого зрозуміло, що точка S′ є дійсним зображенням джерела S (див. п.1.3), котре є віддалене від полюса дзеркала на відстань f = L, а відстань d від самого джерела S до полюса перевищує фокусну відстань F на шукану величину l: d = F + l. Отже, згідно з формулою дзеркала (1.6),
\(\frac{1}{F+l}+\frac{1}{L}=\frac{1}{F}\).
Звідси після елементарних викладок одержимо
\(l=\frac{F^{2}}{L-F}\),
і, відтак урахувавши формулу (1.5), дістанемо наступну точну відповідь:
\(l=\frac{R^{2}}{2(2L-R)}\).
Але, позаяк за умовою R << L, обчислення доцільно виконувати за наближеним виразом:
$f\approx \frac{{{R}^{2}}}{4L}$ = 4 мм
Отже, джерело має бути розташоване за полюсом на 4 мм далі від дзеркала, як це разом із побудовою зображення точки S′ показано на рис. 17-1.
Задача 2.17
Промені збіжного конічного пучка, що проходять крізь розсіювальну лінзу з фокусною відстанню F = 30 см, перетинаються на головній оптичній осі на відстані L = 60 см від лінзи.
Визначити,
на яку відстань l зміститься точка сходження променів, якщо лінзу прибрати.
|
Дано: F = 30 см
L = 60 см
|
|
l - ? |
Розв’язання
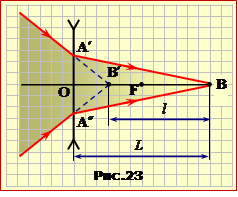
Збіжні промені, що падають на лінзу, йдуть від не точкового джерела. Тож може здатися, що формула лінзи (1.6) є недійсною через невизначеність відстані d. Але завдяки оборотності світлових променів задачу можна "обернути", розглядаючи точку точку сходження самих променів як джерело, а точку сходження продовжень – як його уявне зображення (рис. 23-1), та покласти у формулі (1.6) d = L і f = L – l. Тоді, врахувавши правило знаків, після елементарних перетворень отримаємо відповідь задачі:
|
|
\(\frac{1}{L}-\frac{1}{L-l}=-\frac{1}{F}\) \(\Rightarrow\) \(l=\frac{L^{2}}{L+F}=40\) см. |
(1) |
На завершення зауважимо, що, позаяк порядок доданків у рівнянні (1) не має значення, точку сходження продовжень променів можна формально трактувати як уявний "предмет", а точку сходження самих променів — як його дійсне зображення. Тоді у формулі лінзи –(L – l)= d′ і L = f′.
Задача 2.18
Мураха повзе вздовж головної оптичної осі опуклого дзеркала із фокусною відстанню F зі швидкістю v = 5 мм/с.
1) побудувати зображення мурахи та
2) визначити швидкість його руху u на момент знаходження мурахи на відстані d = 1,5F від дзеркала.
|
Дано: v = 5 мм/с
d = 1,5F
|
|
u - ?
|
Розв’язання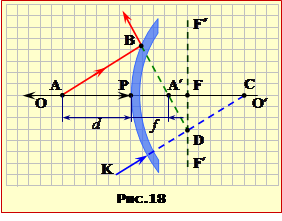
1. Зображення (рис. 18) будуємо в такій послідовності за рекомендаціями (п.1.4, рис. 2.15б):
1) показуємо положення фокальної площини F′F″, яка перетинає головну оптичну вісь ОО′ в точці F на середині радіуса кривини PС дзеркала (ф-ла (1.5));
2) проводимо допоміжний промінь KC у напрямі до центра кривини C дзеркала, і відмічаємо точку перетину D його продовження з фокальною площиною.
3) будуємо хід паралельного до KC допоміжного променя АВ, продовження якого після відбивання теж проходить через точку D;
4) другий необхідний для побудови зображення промінь AP напрямляємо вздовж головної оптичної осі ОО′, тож у точці P він відбивається в протилежному напрямі;
5) у точці перетину A′ продовжень BD і РC указаних ”робочих“ променів отримуємо уявне зображення точки A.
2. Для визначення швидкості зображення u спочатку за формулою (1.10) виразимо зв'язок між координатами (відстанями від дзеркала) f і d, врахувавши, що для опуклого дзеркала f < 0 і d < 0 :
|
$-\frac{1}{F}=\frac{1}{{{d}}}-\frac{1}{f}\quad \Rightarrow \quad f=\frac{Fd}{{{d}}+F}$. |
(1) |
З цього виразу видно, що величина f не є прямо пропорційна до d, отже, на відміну від мурахи, її зображення рухається нерівномірно. Через це шукана швидкість u визначається похідною по часу f′ величини f : u = f′ (див. [І], розділ І, п.1.1). Тож, із виразу (1) за правилом диференціювання частки, отримаємо:
| $u=F\frac{\left( {d}'\left( d+F \right)-d{{\left( d+F \right)}^{\prime }} \right)}{{{\left( d+F \right)}^{2}}}={{\left( \frac{F}{d+F} \right)}^{2}}{d}'$, |
(2) |
Відтак, урахувавши, щоде d′ = $v$ і d = 1,5F, дістанемо наступну відповідь:
|
$u=\frac{v}{{{2,5}^{2}}}=0,8$ мм/с |
(3) |
Отриманий результат показує, що опукле дзеркало дає зменшені не лише розміри зображення, а й швидкісь його руху.
Покажемо також, як можна розв'язати задачу без вищої математики.
Задля цього спочатку за допомогою виразу (1) запишемо наближений вираз шуканої швидкості u ≈ (Δf/Δt) при невеликому переміщенні мурахи відносно дзеркала з відстані d до d + $\Delta d$:
|
$u\approx \frac{F}{\Delta t}\left( \frac{d+v\Delta t}{d+v\Delta t+F}-\frac{d}{d+F} \right)$. |
Відтак, звівши вираз у дужках до спільного знаменника й узявши до уваги, що $\Delta d=v\Delta t$, після спрощень отримаємо
|
$u\approx \frac{{{F}^{2}}v}{\left( d+F \right)\left( d+v\Delta t+F \right)}$ |
|
Зрозуміло, що точність цього виразу при зменшенні проміжку часу, для якого його отрмано, зростатає. Тож у границі $\Delta t\to 0$ він дає точну відповідь, яка збігається з (3).
Малий предмет розглядають крізь лупу із фокусною відстанню F = 5 см так, що зображення утворюється на відстані найкращого зору L = 25 см.
Визначити,
на якій відстані d від предмета розташовано лупу, та яке збільшення \(\Gamma\) вона дає.
|
Дано: F = 5 см
L = 25 см
|
|
d, \(\Gamma\) - ?
|
Розв’язання
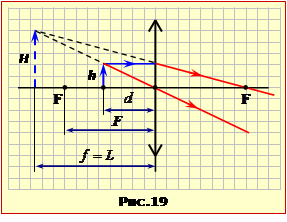
Лупа – то є збирвльна лінза, котра "озброює" око, тобто створює збільшене пряме (неперевернуте) зображення предмета, що розглядається. Таке зображення є уявним (див. п. 1. 3), тому лупа має бути розміщена біля ока на відстані від предмета d < F , аби відстань до зображення складала f = L, як показано на рис. 19. Тож, із формули лінзи (1.6) з урахуванням правила знаків (див. п. 1. 3) отримуємо:
|
\(\frac{1}{d}-\frac{1}{L}=\frac{1}{F}\) \(\Rightarrow\) \(d=\frac{LF}{L+F}\) $\approx $4,2 см. |
(1) |
Відповідно, для збільшення Γ= (L/d) виходить
\(\Gamma=\frac{L+F}{F}\) = 6
Задача 2.20
Визначити:
а) при якій відстані d0 від предмета до лінзи з фокусною відстанню F відстань L між ним і його зображенням на екрані буде мінімальною та
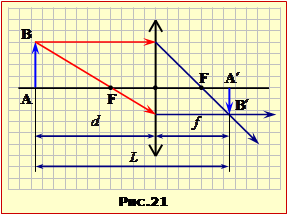 б) її величину L0.
б) її величину L0.
|
Дано: F
|
|
d0 - ?
L0 - ?
|
Розв’язання
Найперше зауважимо, що побачити на екрані можна тільки дійсне зображення. Отже, лінза є збиральною, а предмет розташовано за фокусом, як показано на рис. 21.
Аби знайти загальну відповідь, спочатку встановимо зв'язок між відстанями від предмета до лінзиі d та до зображення (екрана) L, виразивши у формулі лінзи (1.6) відстань f від лінзи до зображення, як
| f = L – d. |
|
Тоді
|
\(\frac{1}{d}+\frac{1}{L-d}=\frac{1}{F}\) \(\Rightarrow\) \(L=\frac{d^{2}}{d-F}\). |
(1) |
Подальший розв'язок можна провести в два способи, використавши:
1. Вищу математику;
2. Алгебру.
Спосіб 1
а) У точці мінімуму функція переходить від спаду до зростання, тому швидкість її зміни, що визначається похідною, дорівнює нулю. Отже, аби отримати відповіді, треба знайти похідну L′(d) функції (1) і прирівняти її до нуля. А саме.
Вираз (1) є часткою функцій φ1 = d2 і φ2 = (F – d). Тож за правилом диференціювання частки
${{\left( \frac{{{\varphi }_{1}}}{{{\varphi }_{2}}} \right)}^{\prime }}=\frac{{{\varphi }_{1}}^{\prime }{{\varphi }_{2}}-{{\varphi }_{1}}{{\varphi }_{2}}^{\prime }}{\varphi _{2}^{2}}$,
і, враховуючи, що ${{\varphi }_{1}}^{\prime }=2d$ i ${{\varphi }_{2}}^{\prime }=1$,
|
\(L^{\prime}=\frac{2d(d-F)-d^{2}}{(d-F)^{2}}=\frac{d(d-2F)}{(d-F)^{2}}\). |
|
Відтак, прирівнявши отриманий вираз до нуля при d = d0, знайдемо першу відповідь:
|
\(\frac{d_{0}( d_{0}-2F)}{( d_{0}-F)}=0\) \(\Rightarrow\) \(d_{0}=2F\). |
|
б) Другу відповідь (величину L0) знайдемо підстановкою \(d = d_{0}=2F\) у вираз (1):
\(L_{0}=\frac{4F^{2}}{2F-F}=4F\).
Принагідно зауважимо, що при отриманих відстанях L0 = 4F (1) і d0 = 2F також і відстань f = 2F. Отже, мінімальна відстань між предметом і його дійсним зображенням спостерігається при їхньому симетричному розташуванню на подвійній фокусній відстані від лінзи.
Спосіб 2
Перепишемо вираз (1) у вигляді квадратного рівняння
|
\(d^{2}-Ld+LF=0\), |
|
корені якого
|
\(d_{1,2}=\frac{L}{2}\left(1\pm\sqrt{1-\frac{4F}{L}}\right)\) |
(2) |
мають бути дійсними бо визначають положення дійсного зображення. Тому лише за умови
\(1-\frac{4F}{L}\ge{0}\) \(\Rightarrow\) \(L\ge{4F}\).
Отже, мінімальна можлива відстань між предметом та його зображенням на екрані (відповідь б)) складає
\(L_{0}=4F\)
і залежить тільки від фокусної відстані лінзи.
Підставивши це значення у вираз (2), дістанемо відповідь а):
\(d_{0}=\frac{L_{0}}{2}=2F\).
Задача 2.21
Лінза дає чітке зображення джерела світла на екрані в двох положеннях на відстані l = 60 см одне від одного.
Визначити
фокусну відстань лінзи F, якщо відстань від неї до екрана L = 1 м.
|
Дано: L = 1 м
l = 60 см
|
|
F - ?
|
Розв’язання
Одразу візьмемо до уваги, що на екрані може утворюватися тільки дійсне зображення, тож лінза є збиральною. 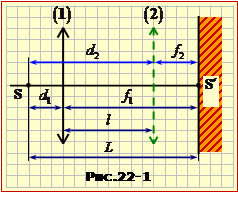
На рис. 22-1 схематично показані точка S, її зображення S′, відповідні положення лінзи та позначені всі потрібні відстані.
Для отримання відповіді простіше за все для кожного випадку записати з урахуванням знаків формулу лінзи (1.6) та відповідно до умови – співвідношеня між величинами, що входять до неї:
|
\(\frac{1}{d_{1}}+\frac{1}{f_{1}}=\frac{1}{F}\) |
(1) |
|
|
\(\frac{1}{d_{2}}+\frac{2}{f_{2}}=\frac{1}{F}\) |
(2) |
|
|
${{f}_{1}}+{{d}_{1}}=L$ |
(3) |
|
|
${{f}_{2}}+{{d}_{2}}=L$ |
(4) | |
|
${{d}_{2}}-{{d}_{1}}=l$ |
(5) |
В отриманій системі рівнянь кількість невідомих (d1, f1, d2, f2, F) збігається із кількістю рівнянь, отже вона є повною. Тож, розв'язавши її, можна серед інших отримати й шукану величину F. Але такий підхід вимагає громіздких викладок і є нераціональним. Натомість доцільно скористатись одним із застосованих у попередній задачі способів, а саме.
I спосіб. Завдяки оборотності світлових променів (п. 1.3), зробивши в рівнянні (5) заміну d2 = f1 , f2 = d1, отримаємо:
|
\(f_{1}-d_{1}=l\), |
(5′) |
і почленно додавши та віднявши рівняння (5′) та (3), дістанемо
\(d_{1}=\frac{L-l}{2}\), \(f_{1}=\frac{L+l}{2}\).
Відтак, підставивши ці вирази в рівняння (1), після нескладних викладок знайдемо відповідь:
\(\frac{2}{L-l}+\frac{2}{L+l}=\frac{1}{F}\) \(\Rightarrow\) \(F=\frac{L^{2}-l^{2}}{4l}=16\) см.
II спосіб. Скористаємось виразами d1 і d2 із задачі 2.19 (формула (6)):
\(d_{1}=\frac{L}{2}\left(1-\sqrt{1-\frac{4F}{L}}\right)\),
\(d_{2}=\frac{L}{2}\left(1+\sqrt{1-\frac{4F}{L}}\right)\).
В такому разі, згідно з співвідношенням (3)
\(l=L\sqrt{1-\frac{4F}{L}}\) \(\Rightarrow\) \(F=\frac{L^{2}-l^{2}}{4L}\) = 16 см.
Задача 2.22
Короткозора людина читає книжку, тримаючи її на відстані d = 16 см від ока, тоді як відстань найкращого зору складає d0 = 25 см.
Визначити
оптичну силу Dc окулярів, які їй потрібні для корекції зору.
|
Дано: d = 16 см
d0 = 25 см
|
|
Dc - ?
|
Розв’язання
Із фізичної точки зору око являє собою збиральну лінзу (кришталик), котра розташована на приблизно однаковій для всіх людей відстані від ″екрана″ (сітківки) такій, що чітке зображення на ній утворюється при відстані від кришталика до предмета d0 = 25 см, яка називається відстанню найкращого зору. Але в людей з дефектами зору ця відстань інша, й це створює великі незручності та перевтомлює око. Тож задля корекції зору поблизу ока розміщують окуляри – допоміжні лінзи, що разом з кришталиком утворюють систему з необхідною для нормального зору оптичною силою (оберненою фокусною відстанню (1.12)), котра дорівнює
|
|
D0 = D + Dc, |
де D і Dc – оптичні сили кришталика та коригуючих лінз (окулярів) нарізно.
Ясна річ, при читанні й з окулярами, і без них, чітке зображення утворюється на одній і тій самій відстані f від кришталика до сітківки ока. Отже, за формулою лінзи (1.6) маємо
|
|
$\frac{1}{{{d}_{0}}}+\frac{1}{f}=D+{{D}_{c}}$, |
|
$\frac{1}{d}+\frac{1}{f}=D$, |
звідки випливає така відповідь:
\(D_{c}=\frac{1}{d}-\frac{1}{d_{0}}=-2,25\) дптр.
Знак ″–″ означає, що для короткозорих людей окуляри виготовляються із розсіювальних лінз.
Задача 2.23
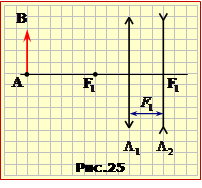 На одній осі зі збиральною лінзою Л1 із заданою фокусною відстанню F1 у фокальній площині встановлено розсіювальну лінзу Л2.
На одній осі зі збиральною лінзою Л1 із заданою фокусною відстанню F1 у фокальній площині встановлено розсіювальну лінзу Л2.
Визначити
її фокусну відстань F2, якщо система створює збільшене в \(\Gamma=2\) рази дійсне зображення предмета, котрий розміщено перед збиральною лінзою на відстані d1 = 3F1.
|
Дано: d1 = 3F1
\(\Gamma=2\)
|
|
F2 - ?
|
Розв’язання
На рис. 25 показано взаємне розташування предмета й лінз, а на на рис. 25-1 — хід променів і необхідні для розрахунку величини F2 відстані.
Ключовою при розрахунку оптичної системи є оборотність променів (див. п. 1.3), що дозволяє віртуальне зображення від одного елемента системи трактувати як зображуваний предмет для наступного. Тому в даній задачі дійсне зображення A2B2 можна розглядати як предмет, а стрілку A1B1 – як його уявне зображення в розсіювальній лінзі Л2. Тож величину F2 будемо шукати за формулою (1.10) із відповідним урахуваням правила знаків (п. 1.3):
|
$-\frac{1}{{{d}_{2}}}+\frac{1}{{{f}_{2}}}=-\frac{1}{{{F}_{2}}}$. |
(1) |
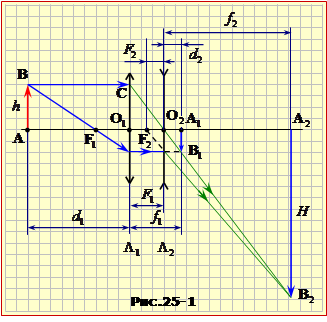
Потрібні для цього величини d2, f2 знайдемо, розглянувши хід променів, рис. 25-1. А саме, з подібності трикутників O2A2B2 і O2O1C випливає, що
$\frac{{{f}_{2}}}{{{F}_{1}}}=\frac{H}{h}\quad \Rightarrow \quad {{f}_{2}}=\Gamma {{F}_{1}}$.
А для визначення величини d2 спочатку за формулою (1.10) знайдемо значення f1, урахувавши, що d1 = 3F1:
|
|
\(\frac{1}{3F_{1}}+\frac{1}{f_{1}}=\frac{1}{F_{1}}\) \(\Rightarrow\) \(f_{1}=\frac{3}{2}F_{1}\). |
|
Отже, позаяк d2 = f1 – F1,
${{d}_{2}}=\frac{1}{2}{{F}_{1}}$.
Відтак підставимо цю величину та знайдене раніше значення ${{f}_{2}}=\Gamma {{F}_{1}}$ у вираз (1) й отримаємо наступну відповідь:
$-\frac{2}{{{F}_{1}}}+\frac{1}{\Gamma {{F}_{1}}}=-\frac{1}{{{F}_{2}}}\quad \Rightarrow \quad {{F}_{2}}=\frac{2}{3}{{F}_{1}}$
Розділ II. Хвильова оптика
|
Хвильова оптика досліджує явища суто хвильової природи, що виходять за рамки геометричної оптики. Тож у процесі роботи за потреби варто звертатися до теоретичного матеріалу з попередньої частини посібника (ч. [4] Коливання та хвилі). Далі подано: 2. Приклади розв’язування задач 3. Задачі для самостійної роботи
|
1. Теоретичні відомості
Із оптичних хвильових явищ у даному посібнику розглянуто наступні:
1.1. Інтерференція світла.
1.2. Дифракція світла.
Принагідно нагадаємо, що основними характеристиками (параметрами) хвиль є амплітуда, період (частота) і фаза (див. [4], розділ ІІІ).
1.1. Інтерференція світла.
|
Інтерференцією називається виникнення в просторі максимумів і мінімумів інтенсивності при накладанні когерентних, тобто, узгоджених за фазою хвиль. В ідеалі такими є неперервні монохроматичні хвилі ([4], розділ ІІІ, п. 1.1) однакової частоти. Але в дійсності світло випромінюється атомами речовини у вигляді окремих порцій-''цугів'' із довільними (за винятком лазерів) початковими фазами. Тому світлові хвилі від різних джерел не можуть бути когерентними й при накладанні не інтерферують. Проте, інтерференцію можна спостерігати, якщо світлову хвилю від одного джерела розділити на окремі, ясна річ, когерентні пучки й звести так, ніби вони приходять у точку спостереження від різних джерел.
Тож, за принципом суперпозиції результуюча напруженість у точці спостереження
або згорнуто
де ${{\varphi }_{0}}=\left( {{\varphi }_{2}}+{{\varphi }_{1}} \right)/2$ – початкова фаза результуючих коливань,
– їхня амплітуда, а
|
|
Відомо, що інтенсивність хвилі є прямо пропорційна квадратові амплітуди, тож за виразом (2.3) для результуючої інтенсивності маємо:
де I – інтенсивніссть, створювана одним джерелом. Отже, I0 ≠ 2I, в чому й полягає явище інтерференції. Iншими словами, інтерференція – то є таке накладання хвиль, при якому результуюча інтенсивність не дорівнює сумі інтенсивностей хвиль, які накладаються. При цьому, залежно від величини \(\delta\), в одих місцях виходить I0 > 2I, а в інших I0 < 2I. Слід одразу сказати, що це не порушує закон збереження енергії, як може здатися, – поява указаних зон означає не виникнення чи зникнення енергії, а лише її перерозподіл у просторі. В цьому легко переконатись, якщо визначати не величину I0 в точці, а середню інтенсивність <I0> в певному об'ємі. Тоді, зважаючи на малість (порядку 10–7 м) довжини хвилі й велику частоту (порядку 1014те, що середнє за період значення функції <cos2> = 1/2, з виразу (2.5) скрізь матимемо очікувану величину <I0> = 2I. |
2) Різниця ходу променів. Фаза кожної зі складових хвиль, яка визначає результуючу інтенсивність I0 у точці спостереження P (рис. 17.1 ), залежить від довжини хвилі λ та відстані l до джерела (див. ([4], ф-ла (3.5)), як
|
$\varphi =\frac{2\pi }{\lambda }l$. |
|
Відповідно, при поширенні світла у вакуумі (на практиці в повітрі) різниця фаз
|
\(\delta=\frac{2\pi}{\lambda}\Delta_{0}\), |
(2.6) |
де величина
|
${{\Delta }_{0}}={{l}_{2}}-{{l}_{1}}$ |
(2.6а) |
називається геометричною різницею ходу променів.
При поширенні обох променів в однорідному середовищі з показником заломлення n
|
$\delta =\frac{2\pi }{{{\lambda }_{0}}}\Delta $, |
(2.7) |
де величина
|
$\Delta$ = $n{{\Delta }_{0}}$ = $n\left( {{l}_{2}}-{{l}_{1}} \right)$ |
(2.7а) |
називаються оптичною різницею ходу променів. При поширенні променів у середовищах із різною оптичною густиною (показником заломлення) цей вираз набувє вигляду:
|
$\Delta ={{n}_{2}}{{l}_{2}}-{{n}_{1}}{{l}_{1}}$. |
(2.7б) |
Стосовно оптичної різниці ходу треба зробити наступне важливе зауваження. Одним із випадків утворення когерентних променів є часткове відбивання світла на межі поділу прозорих середовищ із різною оптичною густиною (показником заломлення), приміром, від поверхонь тонкої прозорої пластини в якомусь середовищі. При цьому, як свідчить теорія й практика, спостерігається ефект ''врати півхвилі'', а саме, стрибкова зміна на π фази відбитої від оптично більш густої речовини хвилі. В такому разі
|
$\Delta =\left( {{n}_{2}}{{l}_{2}}-{{n}_{1}}{{l}_{1}} \right)-\frac{\lambda }{2}$. |
(2.7в) |
|
3). Розподіл інтенсивностей. Якщо переміщуватись у зоні накладання когерентних світлових хвиль так, аби різниця фаз \(\delta\) монотонно змінювалася, то величина \(\cos^{2}(\delta/2)\) у формулі (2.4) буде періодично змінюватися від 1 до 0 і навпаки, через що величина I0 почергово набуватиме максимального й мінімального значення. Тож на поставленому впоперек до напрямку поширення світла ектрані спостерігатиметься інтерференційна карина – сукупність світлих і темних смуг, положення котрих задовольняє певні умови. А саме. Із виразу (2.5) випливає, що інтенсивність I0 у точці спостереження буде максимальною (4I), якщо різниця фаз складових хвиль дорівнює
і мінімумальною (0) при
Відповідно, з виразу (2.6a), випливють наступні зручні для розрахунків умови максимумів
і мінімумів інтерференції
Тобто,
Таким чином, визначення результату інтерференції зводиться до встановлення різниці ходу променів, які приходять у дану точку. На завершення необхідно зробити наступне важливе зауваження. Реальні джерела світла мають помітні розміри і, крім лазерів, не є строго монохроматичними. Тож справжні й уявні джерела, що створюються при поділі світлових пучків, не бувають сповна когерентними. Через це реально можна бачити тільки обмежену кількість інтерференційних смуг у невеликій області простору напроти джерел. |
4). Інтерференційні схеми. На практиці для поділу світлової хвилі на когерентні пучки й спостереження інтерференції використовують різні способи – ''інтерференційні схеми'', що ґрунтуються на відбиванні та заломленні світла. Як приклад можна навести інтерференцію при відбиванні світла від тонких прозорих пластин, зокрема добре відоме райдужне забарвлення бензинових плівок на поверхні води, або мильних бульбашок, видуванням яких полюбляють забавлятися діти. Детальніше деякі з інтерференційних схем розглянуто далі (п. 2.1).
1.2. Дифракція світла
|
Дифракцією називаються явища, що зумовлені здатністю хвиль огинати перешкоди й заходити в область їхньої геометричної тіні. Помітно вираженою дифракція є при проходженні світла крізь малий отвір або вузьку щілину чи дифракційну ґратку – сукупність щілин у непрозорому екрані, ширина котрих є сумірною з довжиною світлових хвиль: (10 ÷ 100)\(\lambda\). Аналіз дифракційних явищ ґрунтується на емпіричному принципі Гюйгенса-Френеля, згідно з яким
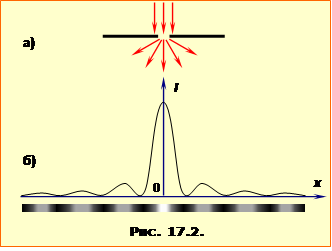
В усіх точках хвильової поверхні фаза хвилі однакова, тож вторинні хвилі є когерентні й інтерферують при накладанні. Тому при проходженні світла крізь малий отвір або вузьку щілину (рис.17.2а) на поставленому за нею екрані спостерігається не просто розмита світна пляма, а сукупність дифракційних максимумів і мінімумів (рис.17.2б) – світлих і темних кілець, чи смуг.
|
|
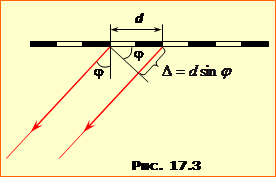
Дифракційні смуги від однієї щілини є слабкі. Але інтенсивність дифракційних максимумів різко збільшується у дифракційній гратці – впорядкованій сукупності великої кількості вуззьких щілин. Найпростіша дифракційна ґратка являє собою плоску прозору пластинку, на поверхні якої створено однакові вузькі прозорі смуги (щілини), розділені однаковими непрозорими проміжками (рис.17.3). Відстань d між сусідніми щілинами називається періодом ґратки і є одним з її основних параметрів. Разом із періодом використовують також "сталу дифракційної ґратки" n = d–1 (1/м) – кількість щілин на одиницю її довжини. Ще одним параметром ґратки є загальна кількість щілин N. Для дифракційних ґраток високого класу d ~ 1 мкм (10–6 м) і N ~ 105.
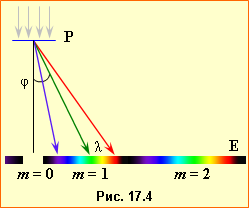
При опроміненні паралельними променями за ґраткою через дифракцію під будь-яким заданим кутом дифракції \(\varphi\) поширюється N когерентних світлових пучків, унаслідок інтерференції котрих на розташованому за ґраткою екрані створюється складна дифракційна картина, що являє собою сукупність головних максимумів інтенсивності, що розділені великою кількість слабких побічних максимумів (рис. 1), у яких зосереджена лише незначна енергія, що проходить крізь гратку Положення головних максимумів визначаться наступною дифракційною формулою:
де d – період ґратки, \(\varphi\) – кут дифракції, \(\lambda\) – довжина хвилі світла, яким опромінюється ґратка, m – ціле число, що називається порядком дифракційного спектра. Велика інтенсивність і умова головних максимумів (2.10) мають просте пояснення. З рис. 17.3 можна зрозуміти, що величина \(\Delta=d\sin\varphi \) – то є різниця ходу променів, які йдуть від сусідніх щілин. Отже, при виконанні умови (2.10) фази коливань електричного поля від усіх N щілин є кратні до \(2\pi\), тож результуюча амплітуда світлової хвилі дорівнює \(E=NE_{1}\), а інтенсивність
де N – загальна кількість щілин у ґратці й \(I_{1}\) – інтенсивність, яка створюється в точці відповідного головного максимума однією щілиною. |
Згідно з умовою (2.10), кожній довжині хвилі \(\lambda\) відповідає свій кут дифракції \(\varphi\), тож і положення головного максимума заданого порядку m. Тому, якщо на ґратку P з відомим періодом напрямити пучок білого світла, то на екрані E замість вузких білих смуг утворюються дифракційні спектри – широкі смуги, що забарвлені в усі кольори веселки (рис.17.4). Виняток становить лише центральний максимум (m = 0), для якого \(\sin\varphi=0\), й умова (2.10) виконується для всіх довжин хвилі.
|
Згідно з умовою (2.10), вимірявши кут дифракції \(\varphi\) (або координату відповідної точки на екрані), можна визначити довжину хвилі \(\lambda\) світла, що дає дифракційний максимум у даній точці: \(\lambda=\frac{d\sin\varphi}{m}\). Це зумовлює практичне застосування дифракційної ґратки в якості спектроаналізатора. А здатність розгортати світло в спектр зумовлює її використання для отримання пучків монохроматичного світла із заданою довжиною хвилі. |
2.1. Інтерференція світла
У наведених текстах по замовчуванню свтлові промені падають на поверхоню поділу середовищ по нормалі, а в інших випадках їхні напрями відраховуються від нормалі.
Задача 2.1. Світло з довжиною хвилі \(\lambda=620\) нм від одного джерела після проходження крізь дві паралельні щілини потрапляє на паралельний до них екран. Визначити ширину \(\Delta{x}\) інтерференційних смуг на екрані при відстанях: між щілинами d = 0,4 мм; між щілинами та екраном l = 0,5 м.
Задача 2.2. У схемі ″дзеркало Ллойда″ (рис. 3.11) монохроматичне світло від джерела S, частково прямо, а частково після відбивання від дзеркала Дз, потрапляє на екран Е й при малій відстані h створює на ньому інтерференційні смуги. Визначити довжину світлової хвилі λ, якщо при l = 1 м зміна величини h на Δh = 0,6 мм змінює відстань між смугами в η = 1,5 раза.
Задача 2.3. Скляний (n = 1,5) клин із кутом \(\varphi=2^{\prime}\) опромінюють світлом із довжиною хвилі \(\lambda=600\) нм. Визначити ширину x інтерференційних смуг, що утворюються у відбитих променях.
Задача 2.4. Дві складені квадратні прозорі пластини зі стороною a = 20 см, між якими з одного краю вміщено тонку дротину, опромінюють світлом з довжиною хвилі λ = 640 нм. Визначити, при якій найбільшій товщині дротини d інтерференційні смуги, що утворюються, буде можна бачити неозброєним оком із роздільною здатністю δ = 0,2 мм.
Задача 2.5. Прозору мильну плівку (n = 1,33) опромінюють білим світлом під кутом \(\alpha=30^{\circ}\). Визначити товщину d плівки, якщо червоне світло (\(\lambda_{1}=0,64\) мкм) від неї повністю відбивається, а фіолетове (\(\lambda_{2}=0,40\) мкм) не відбивається взагалі.
Задача 2.1.
Світло з довжиною хвилі \(\lambda=620\) нм від одного джерела після проходження крізь дві паралельні щілини потрапляє на паралельний до них екран.
Визначити
ширину \(\Delta{x}\) інтерференційних смуг на екрані при відстанях: між щілинами d = 0,4 мм; між щілинами та екраном l = 0,5 м.
|
Дано: \(\lambda=620\) нм = 6,2·10–7 м
d = 0,4 мм = 0,4·10–3 м
l = 0,5 м
|
|
\(\Delta{x}\) - ?
|
Розв’язання
На рис. 1 схематично показано ''джерела'' світла (отвори S1 і S2) і промені S1A та S2A, що потрапляють у якусь точку А на екрані.
Світлові хвилі, що проходять крізь отвори, є когерентні (див. п.1.1), тому внаслідок інтерференції на екрані виникають світлі й темні смуги, ширина яких (відстань \(\Delta{x}\) між сусідніми максимумами чи мінімумами), відповідно до умов (2.9), залежить від різниці ходу указаних променів
|
Δ = l2 – l1, |
(1) |
яку не важко визначити за допомогою рис. 1. Для цього, уведемо позначення AD = \({x}\) і запишемо:
$\left\{ \begin{align} & l_{2}^{2}={{l}^{2}}+{{\left( x+\frac{d}{2} \right)}^{2}} \\ & l_{1}^{2}={{l}^{2}}+{{\left( x-\frac{d}{2} \right)}^{2}} \\ \end{align} \right.\Rightarrow l_{2}^{2}-l_{1}^{2}={{\left( x+\frac{d}{2} \right)}^{2}}-{{\left( x-\frac{d}{2} \right)}^{2}}$
Далі, взявши до уваги співвідношення (1), за допомогою формули різниці квадратів після спрощень дістанемо:
| $\Delta \cdot \left( {{l}_{1}}+{{l}_{2}} \right)=2dx$ |
(2) |
За умовою $d\ll l$, отже, практично без утрати точності можна прийняти l1 = l2 = l і переписати вираз (2) як
$\Delta \cdot l=dx$.
Звідси, урахувавши, що за формулами (2.9) на ширині смуги (відстані між сусідніми мінімумами, чи максимумами) різниця ходу променів змінюється на одну довжину хвилі, отримаємо наступну відповідь задачі:
\(\Delta{x}\) = $\frac{l}{d}\lambda $ $\approx $ 0,8 мм.
Розглянутий спосіб спостереження інтерференції називається "схемою Юнга" по імені вченого, хто вперше його продемонстрував.
Задача 2.2.
У схемі ″дзеркало Ллойда″ (рис. 2) монохроматичне світло від джерела S, частково прямо, а частково після відбивання від дзеркала Дз, потрапляє на екран Е і при малій відстані h створює на ньому інтерференційні смуги.
Визначити
довжину світлової хвилі λ, якщо при l = 1 м зміна величини h не Δh = 0,6 мм змінює відстань між смугами в η = 1,5 раза.
|
Дано: l = 1 м Δh = 0,6 мм η = 1,5 |
|
λ – ? |
Розв’язування
Можна вважати, що, подібно до попередньої задачі, на екрані накладаються промені від двох когерентних джерел: реального S і розташованого на відстані d = 2h його зображення S′. Відміна полягає лише в тому, що через ″перекидання″ фази при відбиванні (″втрату півхвилі″, п. 1.1, 2)), світлі й темні смуги на екрані обмінюються місцями. Але це ніяк не впливає на ширину смуги (відстань між інтерференційними мінімумами чи максимумами), тож можна скористатися результатом попередньої задачі, а саме. Позаяк за умовою ширина смуги змінилася від Δx до (Δx/η), а відстань між джерелами – від 2h до 2(h + Δh), то, згідно з формулою (1) із задачі 2.1, можна скласти наступну систему рівнянь із якої знайти відповідь задачі:
|
|
|
|
Задача 2.3
Скляний (n = 1,5) клин із кутом \(\varphi=2^{\prime}\) опромінюють світлом із довжиною хвилі \(\lambda=600\) нм.
Визначити
ширину x інтерференційних смуг, що утворюються у відбитих променях.
|
Дано: n = 1,5
φ = 2′
λ = 600 нм
|
|
x - ? |
Розв’язання
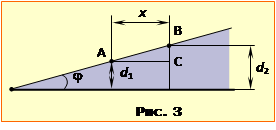
Через мализну кута клина можна вважати, що падаючі та відбиті промені в кожній точці поширюються вздовж одного напряму, як схематично показано на рис. 3. В такому разі ширина інтерференційних смуг $x$ задовольняє співвідношення
| ${{d}_{2}}-{{d}_{1}}=x\varphi $ $\Rightarrow $ $x=\frac{{{d}_{2}}-{{d}_{1}}}{\varphi }$, |
(1) |
де d1, d2 – товщини клина в точках утворення сусідніх інтерференційних мінімумів, або максимумів. При цьому величину ${{d}_{2}}-{{d}_{1}} $ легко знайти, позаяк вона визначає зміну оптичної різниці ходу $\Delta $ відбитих променів на відстані $x$. Справді, як неважко збагнути з рис. 3, величина $\Delta =2nd$, де $d$ − товщина клина в точці падіння світлового променя. Отже,
| ${{\Delta }_{2}}-{{\Delta }_{1}}=2n\left( {{d}_{2}}-{{d}_{1}} \right)$. |
|
А за умовами (2.9) зміна різниці ходу променів на ширині смуги
| ${{\Delta }_{2}}-{{\Delta }_{1}}=\lambda $, |
|
тож
| ${{d}_{2}}-{{d}_{1}}=\frac{\lambda }{2n}$. |
|
Відтак, підставивши цей результат у вираз (1), отримаємо загальну
|
$x=\frac{\lambda }{2n\varphi }$ |
(3) |
і, після обчислень (φ в рад!), кількісну відповідь:
|
$x$ = 0,34 мм. |
|
Задача 2.4
Дві складені квадратні прозорі пластини зі стороною a = 20 см, між якими з одного краю вміщено тонку дротину, опромінюють світлом з довжиною хвилі λ = 640 нм.
Визначити,
при якій найбільшій товщині дротини d інтерференційні смуги, що утворюються, буде можна бачити неозброєним оком із роздільною здатністю δ = 0,2 мм.
|
Дано: a=20см λ=640нм δ=0,2мм |
|
d – ? |
Розв’язання
Роздільна здатність ока – то є найменша відстань між об'єктами, котрі при розгляданні неозброєним оком ще сприймаються відокремлено. У даній задачі – це темні й світлі смуги, що виникають через інтерференцію відбитих від суміжних поверхонь пластин променів. Формально їх можна вважати такими, що відбиваються від повітряного (n = 1) клина, тож дана задача по суті відрізняється від попередньої лише постановкою: задано не кут клина, а найменшу допустиму ширину інтерференційних смуг, що утворюються. Тому, зробивши у виразі (3) із задачі 2.3 заміну
x = δ,
одразу отримуємо максимальний допустимий кут φmax між пластинами
${{\varphi }_{\max }}=\frac{\lambda }{2\delta }$
і максимальну відстань dmax між їхніми краями:
${{d}_{\max }}=\frac{a\lambda }{2\delta }$.
Обчислення дають
${{d}_{\max }}$ = 0,32 мм.
Отже, узявши до уваги існуючі номінали, отримуємо наступний максимальний можливий діаметр дроту:
d = о,3 мм.
Задача 2.5
Прозору мильну плівку (n = 1,33) опромінюють білим світлом під кутом \(\alpha=30^{\circ}\).
Визначити
товщину d плівки, якщо червоне світло (\(\lambda_{1}=0,64\) мкм) від неї повністю відбивається, а фіолетове (\(\lambda_{2}=0,40\) мкм) не відбивається взагалі.
|
Дано: n = 1,33
\(\alpha=30^{\circ}\)
\(\lambda_{1}=0,64\) мкм
\(\lambda_{2}=0,40\) мкм
|
|
d - ?
|
Розв’язання
При опроміненні плівки під заданим кутом \(\alpha\) утворюється сукупність відбитих когерентних (див. п. 1.1) променів, два з яких показано на рис. 5. Ці промені при проходженні крізь лінзу (або кришталик ока) накладаються й, залежно від довжини хвилі, підсилюються, або послаблюються через інтерференцію. Тому безколірна плівка при опроміненні білим світлом набуває забарвлення, що визначається довжиною хвилі підсилених ($\lambda_{1}$) та послаблених ($\lambda_{2}$) променів. При цьому величини ($\lambda_{1}$) і ($\lambda_{2}$) за формулами (2.9) залежать від різниці ходу $\Delta$ (2.7б) променів 2 і 1, яка визначається шуканою товщиною плівки $d$ та заданими показником заломлення $n$ і кутом падіння \(\alpha\).
| $\Delta =\frac{2d}{\cos \beta }-2d\operatorname{tg}\beta \cdot \sin \alpha -\frac{\lambda }{2}$ |
|
$\Delta =2d\sqrt{{{n}^{2}}-{{\sin }^{2}}\alpha }-\frac{\lambda }{2}$. |
(1) |
Тож за умовою максимумів (2.9а), для червоного світла (\(\lambda_{1}\))
| $2d\sqrt{{{n}^{2}}-{{\sin }^{2}}\alpha }-\frac{{{\lambda }_{1}}}{2}={{m}_{1}}{{\lambda}_{1}}$ $\Rightarrow $ $2d\sqrt{{{n}^{2}}-{{\sin }^{2}}\alpha }=\frac{2{{m}_{1}}+1}{2}{{\lambda }_{1}}$. |
(2) |
Аналогічно для фіолетового світла (\(\lambda_{2}\)) за умовою мінімумів (2.9б)
|
\(2d\sqrt{{{n}^{2}}-{{\sin }^{2}}\alpha }=\frac{2{{m}_{2}}+1}{2}{{\lambda }_{2}}\) $\Rightarrow$ $2d\sqrt{{{n}^{2}}-{{\sin }^{2}}\alpha }=\left({{m}_{2}}+1 \right){{\lambda }_{2}}$ |
(3) |
|
$\frac{2{{m}_{1}}+1}{2\left( {{m}_{2}}+1 \right)}=\frac{{{\lambda }_{2}}}{{{\lambda }_{1}}}=\frac{5}{8}$, |
|
і, позаяк у лівій частині цієї пропорції можуть фігурувати тільки цілі числа, доходимо висновку, що
m1 = 2 Можна вважатиі m2 = 3.
Відтак за будь-якою з формул (2) чи (3) після обчислень отримаємо наступну відповідь:
d = 0,65 мкм.
2.2. Дифракція світла
Задача 2.6. Видиме світло, що містить усі кольори від фіолетового (λ1 = 390 нм) до червоного (λ2 = 750 нм), після проходження крізь дифракційну ґратку потрапляє на екран. Визначити кількість дифракційних спектрів N, яку буде видно по один бік екрана.
Задача 2.7. Дифракційну ґратку, що містить n = 45 штрихів на 1 мм, опромінюють монохроматичним світлом. Визначити його довжину хвилі \(\lambda\), якщо кут між напрямами на головні дифракційні максимуми порядків m1 = 1 та m2 = 2 складає \(\Theta=1,6^{\circ}\).
Видиме світло, що містить усі кольори від фіолетового (λ1 = 390 нм) до червоного (λ2 = 750 нм), після проходження крізь дифракційну ґратку потрапляє на екран.
Визначити,
кількість дифракційних спектрів N, яку буде видно по один бік екрана.
|
Дано: λ1 = 390 нм λ2 = 750 нм |
|
N – ? |
Розв'язання
В умові не вказано відстань $h$ від ґратки до екрана та його ширину, тож може здатися, що задача є некоректна. Проте це не так, як показує аналіз залежносі від довжини хвилі $\lambda $ положення на екрані $Е$ (рис. 2.6)
$x=h\operatorname{tg}\varphi $
дифрагованих променів з різною довжиною хвилі, а саме. Зважаючи на специфіку функції $\operatorname{tg}\varphi $, при зміні кута дифракції і довжини хвилі в області великих значень зміна величини $x$ різко пришвидшується, так що довгохвильова зона дифракційнго спектра на екрані виявляється сильно розтягненою порівняно з корткохвильовою. Через це червона межа ((${{\lambda }_{2}}$)) одного спектра може опинитися від центра екрана далі, ніж фіолетова (${{\lambda }_{1}}$) наступного. В такому разі, через накладання променів з різною довжиною хвилі, в зоні перекриття впорядкованого розташування кольорів на екрані, тобто дифракційного спектра, не буде.
Отже, всупереч висловленим напочатку сумнівам, кількість спектрів, які можна побачити на екрані, залежить не від його розмірів і відстані до ґратки, а від межових кутів спектрів, які визначаються формулою (2.10). Зокрема, для сусідніх спектрів
$d\sin {{\varphi }_{2}}=m{{\lambda }_{2}}$
і
$d\sin {{\varphi }_{1}}=(m+1){{\lambda }_{1}}$,
де ${{\varphi }_{2}}$ і ${{\varphi }_{1}}$ – кути дифракції для червоних (${{\lambda }_{2}}$) променів у спектрі порядку $m$ та фіолетових (${{\lambda }_{1}}$) у наступному. При цьому умовою перекривання спектрів є
${{\varphi }_{2}}$ > ${{\varphi }_{1}}$,
отже,
m${{\lambda }_{2}}$ > (m+1)${{\lambda }_{1}}$.
Відтак, розв’язавши цю нерівність, отримаємо
$m$ > $\frac{{{\lambda }_{1}}}{{{\lambda }_{2}}-{{\lambda }_{1}}}$ $\Rightarrow $ $m$ > 1,1.
Позаяк за змістом число $m$ є ціле, отриманий розв'язок означає, що перекривання спектрів починається з другого порядку. Таким чином, на екрані буде видно весь спектр першого порядку й частину другого від початку до довжини хвилі ${{\lambda }}$, для якої кут дифракції ${{\varphi }}$ збігається з кутом дифракції ${{\varphi }_{1}}$ фіолетових променів (${{\lambda }_{1}}$) у спектрі третього порядку. Отже,
$\left\{ \begin{array}{*{35}{l}} {} & d\sin {{\varphi }_{1}}=2\lambda \\ {} & d\sin {{\varphi }_{1}}=3{{\lambda }_{1}} \\\end{array} \right.\quad \Rightarrow \quad \lambda =\frac{3}{2}{{\lambda }_{1}}=585$ нм,
що відповідає жовтому кольору.
Задача 2.7
Дифракційну ґратку, що містить n = 45 штрихів на 1 мм довжини, по нормалі опромінюють монохроматичним світлом.
Визначити
його довжину хвилі \(\lambda\), якщо кут між напрямами на головні дифракційні максимуми порядків m1 = 1 та m2 = 2 складає \(\Theta=1,6^{\circ}\).
|
Дано: n = 45 1/мм
m1 = 1
m2 = 2
Θ = 1,6°
|
|
λ - ?
|
Розв’язання
Відповідно до дифракційної формули (2.10),
| $d\sin \varphi ={{m}_{1}}\lambda $, |
(1) |
|
|
\(\d\sin(\varphi+\Theta)=m_{2}\lambda\), |
(2) |
де \(\varphi\) – кут дифракції для першого і \(\(\varphi+\Theta)\) для другого головного максимума (рис.1), і d – період гратки, що визначається кількістю штрихів на одиницю довжини ґратки як
\(d=\frac{1}{n}\).
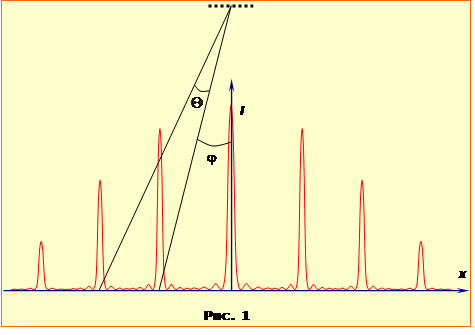
Далі подамо вираз (2) у вигляді
|
|
\(\frac{m_{2}\lambda}{d}=\sin\varphi\cos\Theta+\sin\Theta\cos\varphi\) |
|
і, зробивши заміну
\(\cos\varphi=\sqrt{1-\sin^{2}\varphi}\)
і, взявши до уваги, що 1,6° = 0,028 рад << 1, отже, \(\cos\Theta=1\) і \(\sin\Theta=\Theta\) (рад), отримаємо:
\(\frac{m_{2}\lambda}{d}=\sin\varphi+\Theta\sqrt{1-\sin^{2}\varphi}\).
Звідси, врахувавши, що за формулою (1)
\(\sin\varphi=m_{1}\lambda/d\),
після перетворень і обчислень дістанемо наступну загальну відповіль:
\(\lambda=\frac{\Theta}{N\sqrt{(m_{2}-m_{1})^{2}+m_{1}^{2}\Theta}}=\frac{\Theta}{N\sqrt{1+\Theta^{2}}}\approx\frac{\Theta}{N}\)
та числове значення шуканої довжини хвилі:
\(\lambda\approx{620}\) нм.
Інтерференція світла
У наведених текстах під кутами зору маються на увзі кути падіння, чи заломлення променів, які по тому потрапляють в око.
|
2.8. |
Чи змінюється при інтерференції інтенсивність кожної з хвиль, які накладаються? [Ні] |
|
2.9. |
Яку частку від ширини інтерференційної смуги на екрані складає відстань між точками з максимальною та половинною яскравістю при двопроменевій ітерференції? [Чверть] |
|
2.10. |
Визначити довжини світлових хвиль, які будуть: а) максимально підсилені та б) максимально послаблені при накладанні когерентних променів білого (λ = 400 ÷ 760 нм) світла, якщо іхня різниця ходу складає 2 мкм. [а) 400 нм, 500 нм, 668 нм; б) 444 нм, 571 нм] |
|
2.11. |
На рис. 17.6 показано ”інтерференційну схему Ллойда“, що складається з горизонтального лінійного монохроматичного джерело світла S, паралельного до нього дзеркала AB і вертикального екрана Е, на якому при малій відстані h можна бачити сукупність світлих і темних інтерференційних смуг. Пояснити: 1) як вони виникають й побудовою визначити область інтерференції на екрані; 2) чому величина h має бути малою? |
|
2.12. |
При опроміненні плоскоопуклої лінзи, опуклим боком покладену на плоску скляну пластину, в околі точки дотику виникають концентричні світлі й темні кільцеві смуги, так звані ”кільця Ньютона“. Поясніть, як вони утворюються й чим відрізняються при спогляданні у відбитих променях і на просвіт. |
|
2.13. |
При вийманні з мильного розчину вертикальної дротяної рамки утворюється тонка прозора плівка, котра при спогляданні у відбитих сонячних променях має райдужне забарвлення. Чому та в який бік змінюються його кольори від верхнього до нижнього краю рамки? [Через дію сили тяжіння; в бік червоного] |
|
2.14. |
Паралельні світлові промені від одного джерела пропускають уздовж двох однакових прозорих циліндрів, один з яких відкачано, а інший заповнено вуглекислим газом (показник заломлення \(n=1,001\)). Знайти різницю ходу цих променів при довжині циліндрів 10 см. [\(0,1\) мм] |
|
2.15. |
Два точкові когерентні джерела світла розташовано на відстані \(0,5\) м від екрана. Чому дорівнює відстань між інтерференційними максимумами, що утворюються на екрані при відстані між джерелами \(0,4\) мм і довжині світлової хвилі \(620\) нм)? [\(0,8\) мм] |
|
2.16. |
Для святого Миколая, котрий заглядає в кімнату крізь заледенілу шибку площею \(1\) м2, сріблясті кульки на різдвяній ялинці мають зеленкувате забарвлення, котре відповідає довжині хвилі \(550\) нм. Оцінити додаткову силу тиску на віконну раму, що створюється льодом, якщо його густина дорівнює \(900\) кг/м3, а показник заломлення \(1,3\). [\(\approx{1}\) мН] |
|
2.17. |
Чому дорівнює довжина хвилі світла, яким опромінюють тонкий скляний (n = 1,55) клин із кутом \(2^{\prime}\), якщо відстань між сусідніми інтерференційними смугами, що утворюються, складає 0,3 мм? [541 нм] |
|
2.18. |
Світло від точкового джерела з довжиною хвилі \(580\) нм, відбивається від водяної (показник заломлення \(1,33\)) плівки завтовшки \(0,4\) мкм. Під яким кутом треба дивитися на плівку, аби вона виблискувала найсильніше? $\left[ {{50}^{{}^\circ }} \right]$ |
|
2.19. |
Визначити масу крапельки гасу (густина 0,8 г/см3), котра на поверхні води розтеклася в плівку площею\(S=0,5\) м2, якщо для людини при спостереженні під кутом \(60^{\circ}\) вона має жовтий колір, який відповідає довжині хвилі \(580\) нм. [52 мг] |
Дифракція світла
У пропонованих вправах по замовчуванню прийнято, що світло падає на дифракційну ґратку по нормалі, і кількість спектрів відраховується по один бік від її ґратки.
|
2.20. |
Під якими кутами спостерігаються перші три дифракційні максимуми в ґратці при опромінюванні світлом із довжиною хвилі, що складає 20% від її періоду? [11,5°; 23,5°; 36,8°] |
|
2.21. |
Скільки штрихів на один міліметр має дифракційна ґратка, якщо при її опроміненні світлом із довжиною хвилі \(0,6\) мкм кут дифракції для максимуму п'ятого порядку дорівнює \(17,5^{\circ}\) ? [\(10^2\)] |
|
2.22. |
При якому найменшому періоді дифракційної ґратки можна спостерігати спектр, який включає весь видимий діапазон світлових хвиль (400 ÷ 750) нм? [0,75 мкм] |
|
2.23. |
Ґратку, що містить \(500\) штрихів на 1 см, опромінюють жовтим світлом із довжиною хвилі \(590\) нм. На скільки відрізняються кути дифракції для максимумів першого і другого порядку? [1,4°] |
|
2.24. |
Дифракційна ґратка опромінюється світлом з довжиною хвилі \(620\) нм. Чому дорівнює її період, якщо на віддаленому на \(60\) см екрані відстань між максимумами першого порядку дорівнює \(14,8\) мм? [0,о5 мм] |
|
2.25 |
Дифракційну ґратку, котра має \(2000\) штрихів на сантиметр, опромінюють |
|
2.26 |
Визначити період дифракційної ґратки, при опроміненні котрої білим світлом промені з довжиною хвилі \(656\) нм і \(410\) нм після ґратки поширюються під однаковим кутом\(41^{\circ}\). [5 м] |