physics.zfftt.kpi.ua

Два точкові когерентні джерела світла розташовані на відстані l = 0,5 м від екрана. Довжина хвилі світла \(\lambda=620\) нм. Відстань між джерелами d = 0,4 мм.

Визначити

відстань \(\Delta{x}\) між інтерференційними максимумами на екрані.

Розв’язання

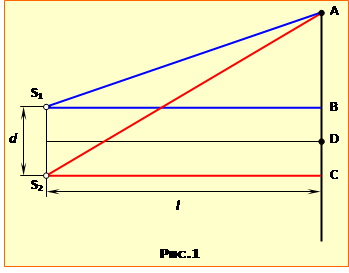
Припустимо, що в точці А на екрані (рис.1) спостерігається максимум інтерференції. Це можливо, якщо різниця ходу \(\Delta\) двох променів S₁A та S₂A задовольняє умові (17.8a):

де m – цілі числа. Знайдемо різницю ходу, скориставшись геометричною побудовою на рис.1. З трикутників S₁AB та S₂AC за теоремою Піфагора маємо:

S₁A² = S₁B² + AB²;     S₂A² = S₂C² + AC².

Відрізки AB та AC відповідно дорівнюють

AB = AD - \(\frac{1}{2}\)BC;    AC = AD + \(\frac{1}{2}\)BC.

Позначимо AD = x. Оскільки S₁B = S₂C = l, BC = d, маємо:

 Різницю квадратів (S₂A² – S₁A²) запишемо у вигляді:

S₂A² – S₁A² = (S₂A – S₁A)(S₂A + S₁A).

Інтерференційна картина в таких випадках завжди спостерігається поблизу центра екрана (точка D на рис.1), тобто \(x\ll{l}\). За цих умов S₂A + S₁A \(\approx\) 2l, S₂A – S₁A = \(\Delta\)отже

S₂A² – S₁A² = \(\Delta\cdot{2l}\).

Підставимо сюди вирази (2) і дістанемо:

\(l^{2}+(x+d/2)^{2}-l^{2}-(x-d/2)^{2}=\Delta{2l}\)    \(\Rightarrow\)    \(x=\frac{\Delta\cdot{l}}{d}\).

Врахувавши умову (1), знаходимо, що точка A, в якій спостерігається максимум інтерференції з номером m, віддалена від точки D на відстань

\(x_{m}=\frac{m\lambda{l}}{d}\).

Точка А₁, в якій спостерігається максимум з номером (m + 1), віддалена від точки О на відстань

\(x_{m+1}=\frac{(m+1)\lambda{l}}{d}\),

отже відстань між максимумами

\(\Delta{x}=x_{m+1}-x_{m}=\frac{\lambda{l}}{d}\).

З останнього виразу зрозуміло, що для покращення умов спостереження інтерференції необхідно збільшувати відстань від джерел до екрана l і зменшувати відстань між джерелами d.

Виконаємо обчислення:

\(\Delta{x}=\frac{6,2\cdot{10^{-7}}\cdot{0,5}}{0,4\cdot{10^{-3}}}=7,75\cdot{10}^{-4}\) м \(\approx{0,8}\) мм.