ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
2. Приклади розв'язування задач
2.1. Інтерференція світла
У наведених текстах по замовчуванню свтлові промені падають на поверхоню поділу середовищ по нормалі, а в інших випадках їхні напрями відраховуються від нормалі.
Задача 2.1. Світло з довжиною хвилі \(\lambda=620\) нм від одного джерела після проходження крізь дві паралельні щілини потрапляє на паралельний до них екран. Визначити ширину \(\Delta{x}\) інтерференційних смуг на екрані при відстанях: між щілинами d = 0,4 мм; між щілинами та екраном l = 0,5 м.
Задача 2.2. У схемі ″дзеркало Ллойда″ (рис. 3.11) монохроматичне світло від джерела S, частково прямо, а частково після відбивання від дзеркала Дз, потрапляє на екран Е й при малій відстані h створює на ньому інтерференційні смуги. Визначити довжину світлової хвилі λ, якщо при l = 1 м зміна величини h на Δh = 0,6 мм змінює відстань між смугами в η = 1,5 раза.
Задача 2.3. Скляний (n = 1,5) клин із кутом \(\varphi=2^{\prime}\) опромінюють світлом із довжиною хвилі \(\lambda=600\) нм. Визначити ширину x інтерференційних смуг, що утворюються у відбитих променях.
Задача 2.4. Дві складені квадратні прозорі пластини зі стороною a = 20 см, між якими з одного краю вміщено тонку дротину, опромінюють світлом з довжиною хвилі λ = 640 нм. Визначити, при якій найбільшій товщині дротини d інтерференційні смуги, що утворюються, буде можна бачити неозброєним оком із роздільною здатністю δ = 0,2 мм.
Задача 2.5. Прозору мильну плівку (n = 1,33) опромінюють білим світлом під кутом \(\alpha=30^{\circ}\). Визначити товщину d плівки, якщо червоне світло (\(\lambda_{1}=0,64\) мкм) від неї повністю відбивається, а фіолетове (\(\lambda_{2}=0,40\) мкм) не відбивається взагалі.
Задача 2.1.
Світло з довжиною хвилі \(\lambda=620\) нм від одного джерела після проходження крізь дві паралельні щілини потрапляє на паралельний до них екран.
Визначити
ширину \(\Delta{x}\) інтерференційних смуг на екрані при відстанях: між щілинами d = 0,4 мм; між щілинами та екраном l = 0,5 м.
|
Дано: \(\lambda=620\) нм = 6,2·10–7 м
d = 0,4 мм = 0,4·10–3 м
l = 0,5 м
|
|
\(\Delta{x}\) - ?
|
Розв’язання
На рис. 1 схематично показано ''джерела'' світла (отвори S1 і S2) і промені S1A та S2A, що потрапляють у якусь точку А на екрані.
Світлові хвилі, що проходять крізь отвори, є когерентні (див. п.1.1), тому внаслідок інтерференції на екрані виникають світлі й темні смуги, ширина яких (відстань \(\Delta{x}\) між сусідніми максимумами чи мінімумами), відповідно до умов (2.9), залежить від різниці ходу указаних променів
|
Δ = l2 – l1, |
(1) |
яку не важко визначити за допомогою рис. 1. Для цього, уведемо позначення AD = \({x}\) і запишемо:
$\left\{ \begin{align} & l_{2}^{2}={{l}^{2}}+{{\left( x+\frac{d}{2} \right)}^{2}} \\ & l_{1}^{2}={{l}^{2}}+{{\left( x-\frac{d}{2} \right)}^{2}} \\ \end{align} \right.\Rightarrow l_{2}^{2}-l_{1}^{2}={{\left( x+\frac{d}{2} \right)}^{2}}-{{\left( x-\frac{d}{2} \right)}^{2}}$
Далі, взявши до уваги співвідношення (1), за допомогою формули різниці квадратів після спрощень дістанемо:
| $\Delta \cdot \left( {{l}_{1}}+{{l}_{2}} \right)=2dx$ |
(2) |
За умовою $d\ll l$, отже, практично без утрати точності можна прийняти l1 = l2 = l і переписати вираз (2) як
$\Delta \cdot l=dx$.
Звідси, урахувавши, що за формулами (2.9) на ширині смуги (відстані між сусідніми мінімумами, чи максимумами) різниця ходу променів змінюється на одну довжину хвилі, отримаємо наступну відповідь задачі:
\(\Delta{x}\) = $\frac{l}{d}\lambda $ $\approx $ 0,8 мм.
Розглянутий спосіб спостереження інтерференції називається "схемою Юнга" по імені вченого, хто вперше його продемонстрував.
Задача 2.2.
У схемі ″дзеркало Ллойда″ (рис. 2) монохроматичне світло від джерела S, частково прямо, а частково після відбивання від дзеркала Дз, потрапляє на екран Е і при малій відстані h створює на ньому інтерференційні смуги.
Визначити
довжину світлової хвилі λ, якщо при l = 1 м зміна величини h не Δh = 0,6 мм змінює відстань між смугами в η = 1,5 раза.
|
Дано: l = 1 м Δh = 0,6 мм η = 1,5 |
|
λ – ? |
Розв’язування
Можна вважати, що, подібно до попередньої задачі, на екрані накладаються промені від двох когерентних джерел: реального S і розташованого на відстані d = 2h його зображення S′. Відміна полягає лише в тому, що через ″перекидання″ фази при відбиванні (″втрату півхвилі″, п. 1.1, 2)), світлі й темні смуги на екрані обмінюються місцями. Але це ніяк не впливає на ширину смуги (відстань між інтерференційними мінімумами чи максимумами), тож можна скористатися результатом попередньої задачі, а саме. Позаяк за умовою ширина смуги змінилася від Δx до (Δx/η), а відстань між джерелами – від 2h до 2(h + Δh), то, згідно з формулою (1) із задачі 2.1, можна скласти наступну систему рівнянь із якої знайти відповідь задачі:
|
|
|
|
Задача 2.3
Скляний (n = 1,5) клин із кутом \(\varphi=2^{\prime}\) опромінюють світлом із довжиною хвилі \(\lambda=600\) нм.
Визначити
ширину x інтерференційних смуг, що утворюються у відбитих променях.
|
Дано: n = 1,5
φ = 2′
λ = 600 нм
|
|
x - ? |
Розв’язання
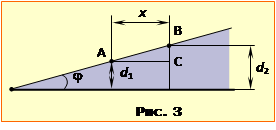
Через мализну кута клина можна вважати, що падаючі та відбиті промені в кожній точці поширюються вздовж одного напряму, як схематично показано на рис. 3. В такому разі ширина інтерференційних смуг $x$ задовольняє співвідношення
| ${{d}_{2}}-{{d}_{1}}=x\varphi $ $\Rightarrow $ $x=\frac{{{d}_{2}}-{{d}_{1}}}{\varphi }$, |
(1) |
де d1, d2 – товщини клина в точках утворення сусідніх інтерференційних мінімумів, або максимумів. При цьому величину ${{d}_{2}}-{{d}_{1}} $ легко знайти, позаяк вона визначає зміну оптичної різниці ходу $\Delta $ відбитих променів на відстані $x$. Справді, як неважко збагнути з рис. 3, величина $\Delta =2nd$, де $d$ − товщина клина в точці падіння світлового променя. Отже,
| ${{\Delta }_{2}}-{{\Delta }_{1}}=2n\left( {{d}_{2}}-{{d}_{1}} \right)$. |
|
А за умовами (2.9) зміна різниці ходу променів на ширині смуги
| ${{\Delta }_{2}}-{{\Delta }_{1}}=\lambda $, |
|
тож
| ${{d}_{2}}-{{d}_{1}}=\frac{\lambda }{2n}$. |
|
Відтак, підставивши цей результат у вираз (1), отримаємо загальну
|
$x=\frac{\lambda }{2n\varphi }$ |
(3) |
і, після обчислень (φ в рад!), кількісну відповідь:
|
$x$ = 0,34 мм. |
|
Задача 2.4
Дві складені квадратні прозорі пластини зі стороною a = 20 см, між якими з одного краю вміщено тонку дротину, опромінюють світлом з довжиною хвилі λ = 640 нм.
Визначити,
при якій найбільшій товщині дротини d інтерференційні смуги, що утворюються, буде можна бачити неозброєним оком із роздільною здатністю δ = 0,2 мм.
|
Дано: a=20см λ=640нм δ=0,2мм |
|
d – ? |
Розв’язання
Роздільна здатність ока – то є найменша відстань між об'єктами, котрі при розгляданні неозброєним оком ще сприймаються відокремлено. У даній задачі – це темні й світлі смуги, що виникають через інтерференцію відбитих від суміжних поверхонь пластин променів. Формально їх можна вважати такими, що відбиваються від повітряного (n = 1) клина, тож дана задача по суті відрізняється від попередньої лише постановкою: задано не кут клина, а найменшу допустиму ширину інтерференційних смуг, що утворюються. Тому, зробивши у виразі (3) із задачі 2.3 заміну
x = δ,
одразу отримуємо максимальний допустимий кут φmax між пластинами
${{\varphi }_{\max }}=\frac{\lambda }{2\delta }$
і максимальну відстань dmax між їхніми краями:
${{d}_{\max }}=\frac{a\lambda }{2\delta }$.
Обчислення дають
${{d}_{\max }}$ = 0,32 мм.
Отже, узявши до уваги існуючі номінали, отримуємо наступний максимальний можливий діаметр дроту:
d = о,3 мм.
Задача 2.5
Прозору мильну плівку (n = 1,33) опромінюють білим світлом під кутом \(\alpha=30^{\circ}\).
Визначити
товщину d плівки, якщо червоне світло (\(\lambda_{1}=0,64\) мкм) від неї повністю відбивається, а фіолетове (\(\lambda_{2}=0,40\) мкм) не відбивається взагалі.
|
Дано: n = 1,33
\(\alpha=30^{\circ}\)
\(\lambda_{1}=0,64\) мкм
\(\lambda_{2}=0,40\) мкм
|
|
d - ?
|
Розв’язання
При опроміненні плівки під заданим кутом \(\alpha\) утворюється сукупність відбитих когерентних (див. п. 1.1) променів, два з яких показано на рис. 5. Ці промені при проходженні крізь лінзу (або кришталик ока) накладаються й, залежно від довжини хвилі, підсилюються, або послаблюються через інтерференцію. Тому безколірна плівка при опроміненні білим світлом набуває забарвлення, що визначається довжиною хвилі підсилених ($\lambda_{1}$) та послаблених ($\lambda_{2}$) променів. При цьому величини ($\lambda_{1}$) і ($\lambda_{2}$) за формулами (2.9) залежать від різниці ходу $\Delta$ (2.7б) променів 2 і 1, яка визначається шуканою товщиною плівки $d$ та заданими показником заломлення $n$ і кутом падіння \(\alpha\).
| $\Delta =\frac{2d}{\cos \beta }-2d\operatorname{tg}\beta \cdot \sin \alpha -\frac{\lambda }{2}$ |
|
$\Delta =2d\sqrt{{{n}^{2}}-{{\sin }^{2}}\alpha }-\frac{\lambda }{2}$. |
(1) |
Тож за умовою максимумів (2.9а), для червоного світла (\(\lambda_{1}\))
| $2d\sqrt{{{n}^{2}}-{{\sin }^{2}}\alpha }-\frac{{{\lambda }_{1}}}{2}={{m}_{1}}{{\lambda}_{1}}$ $\Rightarrow $ $2d\sqrt{{{n}^{2}}-{{\sin }^{2}}\alpha }=\frac{2{{m}_{1}}+1}{2}{{\lambda }_{1}}$. |
(2) |
Аналогічно для фіолетового світла (\(\lambda_{2}\)) за умовою мінімумів (2.9б)
|
\(2d\sqrt{{{n}^{2}}-{{\sin }^{2}}\alpha }=\frac{2{{m}_{2}}+1}{2}{{\lambda }_{2}}\) $\Rightarrow$ $2d\sqrt{{{n}^{2}}-{{\sin }^{2}}\alpha }=\left({{m}_{2}}+1 \right){{\lambda }_{2}}$ |
(3) |
|
$\frac{2{{m}_{1}}+1}{2\left( {{m}_{2}}+1 \right)}=\frac{{{\lambda }_{2}}}{{{\lambda }_{1}}}=\frac{5}{8}$, |
|
і, позаяк у лівій частині цієї пропорції можуть фігурувати тільки цілі числа, доходимо висновку, що
m1 = 2 Можна вважатиі m2 = 3.
Відтак за будь-якою з формул (2) чи (3) після обчислень отримаємо наступну відповідь:
d = 0,65 мкм.