ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
1. Теоретичні відомості
1.2. Дифракція світла
|
Дифракцією називаються явища, що зумовлені здатністю хвиль огинати перешкоди й заходити в область їхньої геометричної тіні. Помітно вираженою дифракція є при проходженні світла крізь малий отвір або вузьку щілину чи дифракційну ґратку – сукупність щілин у непрозорому екрані, ширина котрих є сумірною з довжиною світлових хвиль: (10 ÷ 100)\(\lambda\). Аналіз дифракційних явищ ґрунтується на емпіричному принципі Гюйгенса-Френеля, згідно з яким
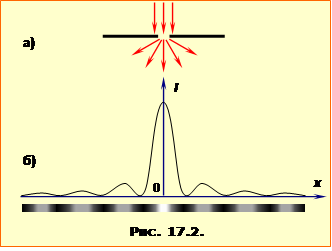
В усіх точках хвильової поверхні фаза хвилі однакова, тож вторинні хвилі є когерентні й інтерферують при накладанні. Тому при проходженні світла крізь малий отвір або вузьку щілину (рис.17.2а) на поставленому за нею екрані спостерігається не просто розмита світна пляма, а сукупність дифракційних максимумів і мінімумів (рис.17.2б) – світлих і темних кілець, чи смуг.
|
|
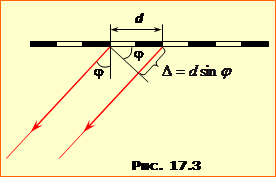
Дифракційні смуги від однієї щілини є слабкі. Але інтенсивність дифракційних максимумів різко збільшується у дифракційній гратці – впорядкованій сукупності великої кількості вуззьких щілин. Найпростіша дифракційна ґратка являє собою плоску прозору пластинку, на поверхні якої створено однакові вузькі прозорі смуги (щілини), розділені однаковими непрозорими проміжками (рис.17.3). Відстань d між сусідніми щілинами називається періодом ґратки і є одним з її основних параметрів. Разом із періодом використовують також "сталу дифракційної ґратки" n = d–1 (1/м) – кількість щілин на одиницю її довжини. Ще одним параметром ґратки є загальна кількість щілин N. Для дифракційних ґраток високого класу d ~ 1 мкм (10–6 м) і N ~ 105.
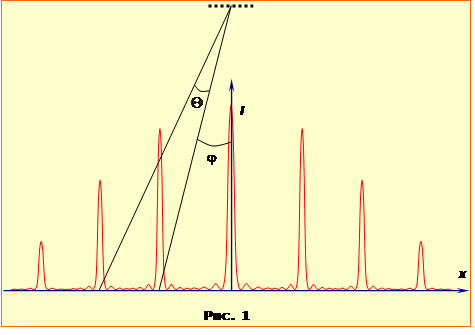
При опроміненні паралельними променями за ґраткою через дифракцію під будь-яким заданим кутом дифракції \(\varphi\) поширюється N когерентних світлових пучків, унаслідок інтерференції котрих на розташованому за ґраткою екрані створюється складна дифракційна картина, що являє собою сукупність головних максимумів інтенсивності, що розділені великою кількість слабких побічних максимумів (рис. 1), у яких зосереджена лише незначна енергія, що проходить крізь гратку Положення головних максимумів визначаться наступною дифракційною формулою:
де d – період ґратки, \(\varphi\) – кут дифракції, \(\lambda\) – довжина хвилі світла, яким опромінюється ґратка, m – ціле число, що називається порядком дифракційного спектра. Велика інтенсивність і умова головних максимумів (2.10) мають просте пояснення. З рис. 17.3 можна зрозуміти, що величина \(\Delta=d\sin\varphi \) – то є різниця ходу променів, які йдуть від сусідніх щілин. Отже, при виконанні умови (2.10) фази коливань електричного поля від усіх N щілин є кратні до \(2\pi\), тож результуюча амплітуда світлової хвилі дорівнює \(E=NE_{1}\), а інтенсивність
де N – загальна кількість щілин у ґратці й \(I_{1}\) – інтенсивність, яка створюється в точці відповідного головного максимума однією щілиною. |
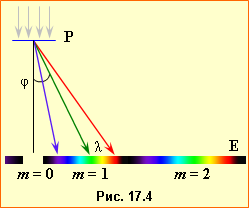
Згідно з умовою (2.10), кожній довжині хвилі \(\lambda\) відповідає свій кут дифракції \(\varphi\), тож і положення головного максимума заданого порядку m. Тому, якщо на ґратку P з відомим періодом напрямити пучок білого світла, то на екрані E замість вузких білих смуг утворюються дифракційні спектри – широкі смуги, що забарвлені в усі кольори веселки (рис.17.4). Виняток становить лише центральний максимум (m = 0), для якого \(\sin\varphi=0\), й умова (2.10) виконується для всіх довжин хвилі.
|
Згідно з умовою (2.10), вимірявши кут дифракції \(\varphi\) (або координату відповідної точки на екрані), можна визначити довжину хвилі \(\lambda\) світла, що дає дифракційний максимум у даній точці: \(\lambda=\frac{d\sin\varphi}{m}\). Це зумовлює практичне застосування дифракційної ґратки в якості спектроаналізатора. А здатність розгортати світло в спектр зумовлює її використання для отримання пучків монохроматичного світла із заданою довжиною хвилі. |