physics.zfftt.kpi.ua

 

 

Задача 16.1. Визначити кут \(\vartheta\) відхилення променя світла, відбитого від двох плоских дзеркал, що утворять двогранний кут \(\varphi\). Площина, у якій лежить падаючий промінь, перпендикулярна ребру двогранного кута.

Задача 16.2. При падінні променя світла на межу поділу двох середовищ відбитий та заломлений промені виявились взаємно перпендикулярними. Визначити кут падіння, якщо відношення показників заломлення середовищ k = 1,5.

Задача 16.3. У точці K на дні непрозорої кубічної посудини лежить маленька важка кулька. Око спостерігача розташоване так, що дно невидиме. У посудину починають наливати воду (n = 1,33). Визначити висоту рівня води h, при якій спостерігач зможе побачити кульку, не змінюючи положення ока, якщо відстань між точками K і N  S = 10 см (див. рис.3).

Задача 16.4. Дві пластини товщиною по h = 2 см кожна з показниками заломлення n₁ = 1,35 i n₂ = 1,95 складені впритул. На поверхні дотику на одній з пластин зафарбовано диск радіусом r = h. На зовнішній поверхні однієї з пластин прямо над центром диска O розміщене точкове джерело світла S (рис.4). Визначити радіус тіні R від диска на зовнішній поверхні іншої пластини у випадку, коли джерело знаходиться на поверхні: А) першої пластини; В) другої пластини.

Задача 16.5. Промінь світла падає під кутом \(\alpha=60^{\circ}\) на скляну (n = 1,5) плоскопаралельну пластину товщиною d = 3 см, що знаходиться в повітрі. Визначити зміщення x променя відносно його початкового напрямку після проходження крізь пластину.

Задача 16.6. Вузький паралельний пучок променів падає на аркуш паперу під кутом \(\alpha=60^{\circ}\) і створює світлову пляму (рис.6). Визначити відстань  S на яку зміститься цятка, якщо на папір покласти скляну (n = 1,5) пластину товщиною d = 5 см.

Задача 16.7. Рибалка, що сидить у човні, розглядає камінчик на дні озера безпосередньо під човном. Рибалці здається, що камінчик знаходиться на глибині h = 3 м. Визначити істину глибину озера H. Показник заломлення води n = 1,33.

Задача 16.8. Хід променя крізь скляну трикутну призму показаний на рис., на якому \(\alpha_{1}=30^{\circ}\), \(\alpha_{2}=60^{\circ}\), \(\delta=45^{\circ}\). Визначити заломний кут призми \(\varphi\).

Задача 16.9. На бічну грань скляної (n = 1,5) призми, що має заломний кут \(\varphi=0,1\) рад, під малим кутом падає промінь світла. Визначити кут відхилення \(\delta\) променя призмою.

Задача 16.10. Промінь світла падає на бічну грань тригранної скляної (n = 1,5) призми з кутом заломлення \(\varphi=60^{\circ}\). Визначити мінімальне значення кута падіння \(\alpha_{m}\), при якому світло буде проходити крізь призму.

 

Задача 16.1

Визначити кут \(\vartheta\) відхилення променя світла, відбитого від двох плоских дзеркал, що утворять двогранний кут \(\varphi\). Площина, у якій лежить падаючий промінь, перпендикулярна ребру двогранного кута.

Дано: \(\varphi\)

\(\vartheta\) - ?

Розв’язання

На рис.1 ребро двогранного кута є перпендикулярним площині рисунка і проходить через точку O. Промінь світла, що падає на одне з дзеркал під кутом \(\alpha_{1}\) (у точці o₁), після відбивання падає на друге дзеркало під кутом \(\alpha_{2}\) (у точці O₂).

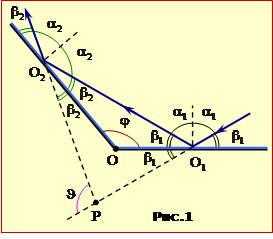
На рис.1 також показані всі кути, необхідні для подальшого розв’язування. Рівність відповідних кутів випливає із закону відбивання (16.5) і очевидних геометричних співвідношень. Кут відхилення \(\vartheta\) – це кут між напрямками променя, відбитого від другого дзеркала в точці O₂ і променя, який падає на перше дзеркало в точку O₁ (див. рис.1). Цей кут є зовнішнім кутом трикутника PO₁O₂, тому

\(\vartheta=2\beta_{1}+2\beta_{2}=2(\beta_{1}+\beta_{2})\).

З трикутника O₁OO₂ маємо

\(\beta_{1}+\beta_{2}=180^{\circ}-\varphi\),

Отже шуканий кут відхилення

\(\vartheta=360^{\circ}-2\varphi\).

Зверніть увагу на те, що цей кут визначається тільки двогранним кутом \(varphi\) і не залежить від напрямку падаючого променя. Зокрема, при \(\varphi=90^{\circ}\) \(\vartheta=180^{\circ}\). Це означає, що будь-який промінь відбивається у зворотному напрямку. Таку ж властивість має і тригранне прямокутне дзеркало. Воно використовується у так званих кутових відбивачах, якими, зокрема, є катофоти автомобілів і велосипедів, а також рефлектори на ранцях школярів.

Задача 16.2

При падінні променя світла на межу поділу двох середовищ відбитий та заломлений промені виявились взаємно перпендикулярними.

Визначити

кут падіння, якщо відношення показників заломлення середовищ k = 1,5.

Дано: k = 1,5 \(\varphi=90^{\circ}\)

\(\alpha\) - ?

Розв’язання

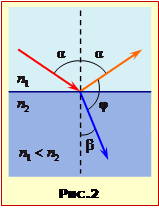На рис.2 показано хід променів для випадку n₁ < n₂. З рисунка видно, що \(\alpha+\varphi+\beta=17=80^{\circ}\) отже при \(\varphi=90^{\circ}\), \(\beta=90^{\circ}-\alpha\), і згідно із законом заломлення (16.6)

\(\frac{\sin\alpha}{\sin(90^{\circ}-\alpha)}\) \(\Rightarrow\) \(\mathrm{tg}\alpha=\frac{n_{2}}{n_{1}}\).

Таким чином шуканий кут падіння

\(\alpha=\mathrm{arctg}\left(\frac{n_{2}}{n_{1}}\right)\).

Числове значення \(\alpha\) залежить від того, яке з середовищ більш оптично густе. Є дві можливості:

1) \(\frac{n_{2}}{n_{1}}=k\)

і

2) \(\frac{n_{2}}{n_{1}}=\frac{1}{k}\).

Відповідно задача має дві числові відповіді:

\(\alpha_{1}=\mathrm{arctg}_{2}{1,5}=56,3^{\circ}\);

\(\alpha_{1}=\mathrm{arctg}_{2}\frac{1}{1,5}=33,7^{\circ}\)

Корисно звернути увагу на те, що за умов задачі незалежно від послідовності розміщення середовищ одне з отриманих значень є кутом падіння, а інше - кутом заломлення.

 

Задача 16.3

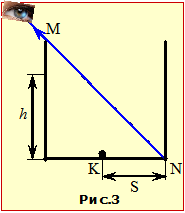У точці K на дні непрозорої кубічної посудини лежить маленька важка кулька. Око спостерігача розташоване так, що дно невидиме (рис.3). У посудину починають наливати воду (n = 1,33).

Визначити

висоту рівня води h, при якій спостерігач зможе побачити кульку, не змінюючи положення ока, якщо відстань між точками K і N S = 10 см (див. рис.3).

Дано: n = 1,33 S = 10 см

h - ?

Розв’язання

Аби спостерігач зміг бачити кульку, частина відбитих нею променів повинна потрапляти в око, як показано на рис.3-1.

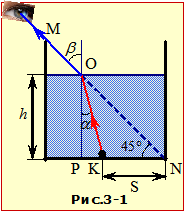Це можливо лише при такій висоті рівня води h, при якій промені KO та OM задовольняють закону заломлення світла (16.6)

\(\frac{\sin\alpha}{\sin\beta}=\frac{1}{n}\).

(1)

(Тут враховано, що показник заломлення повітря практично дорівнює одиниці).

За умовою \(\beta=45^{\circ}\) (посудина - куб), отже

\(\sin\alpha=\frac{1}{2\sqrt{2}}\).

(2)

З рис.3-1 видно, що висота рівня води

\(h=\frac{\mathrm{PK}}{\mathrm{tg}\alpha}\),

(3)

а PK = htg\(\alpha\), PN = htg\(\beta\), S = KN = PN - PK. Отже

\(S=h(\mathrm{tg}\alpha-\mathrm{tg}\beta)\) \(\Rightarrow\) \(h=\frac{S}{\mathrm{tg}\alpha-\mathrm{tg}\beta}\).

Враховуючи співвідношення

\(\mathrm{tg}\alpha=\frac{\sin\alpha}{\sqrt{1-\sin^{2}\alpha}}=\frac{1}{\sqrt{1/\sin^{2}\alpha-1}}\)

та формулу (1), маємо

\(\mathrm{tg}\alpha=\frac{1}{\sqrt{n^{2}/\sin^{2}\beta-1}}\).

Отже

\(h=\frac{S}{\mathrm{tg}\beta-\sqrt{n^{2}/\sin^{2}\beta-1}}\).

Оскільки посудина куб, то \(\beta=45^{\circ}\) і

\(h=\frac{S}{1-1/\sqrt{2n^{2}-1}}=\frac{10}{1-1/\sqrt{2\cdot{1,33}^{2}-1}}=26,9\) см.

 

Задача 16.4

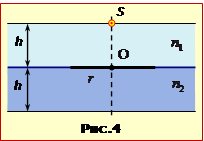Дві пластини товщиною по h = 2 см кожна з показниками заломлення n₁ = 1,35 i n₂ = 1,95 складені впритул. На поверхні дотику на одній з пластин зафарбовано диск радіусом r = h. На зовнішній поверхні однієї з пластин прямо над центром диска O розміщене точкове джерело світла S (рис.4).

Визначити

радіус тіні R від диска на зовнішній поверхні іншої пластини у випадку, коли джерело знаходиться на поверхні:

А) першої пластини;

В) другої пластини.

Дано: h = 2 см \(n_{1}\) = 1,35 \(n_{2}\) = 1,95

R - ?

Розв’язання

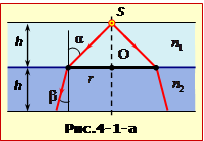А) У цьому випадку світло переходить з оптично менш густого середовища n₁ в більш густе n₂. За законом заломлення (16.6) маємо:

\(R=r+h\mathrm{tg}\beta\).

За умовою r  = h, отже

\(R= h(1+\mathrm{tg}\beta)=h\left(1+\frac{1}{\sqrt{1/\sin^{2}\beta-1}}\right)\).

Величину \(1/\sin^{2}\beta\) знайдемо через співвідношення (16.7), врахувавши, що за умовою задачі (r = h) \(\alpha=45^{\circ}\), отже \(\sin\alpha=1/\sqrt{2}\):

\(\frac{1}{\sin^{2}\beta}=\frac{2n_{2}^{2}}{n_{1}^{2}}\).

Тепер

\(R=h\left(1+\frac{1}{\sqrt{2(n_{2}/n_{1})^{2}-1}}\right)\approx3,1\) см.

 

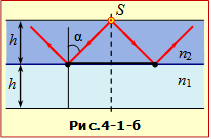Б) В цьому випадку світло падає на межу поділу з більш густого середовища, тому, перш ніж виконувати обчислення, слід з'ясувати, чи зможе світло взагалі пройти через межу поділу. Для цього визначимо граничний кут, для межі заданих речовин (формула (16.7)):

\(\alpha_{0}=\mathrm{arcsin}\left(\frac{n_{1}}{n_{2}}\right)=43,8^{\circ}\).

Згідно з умовою r = h кут падіння \(\alpha=45^{\circ}\), тобто \(\alpha\gt\alpha_{0}\). Отже на межі пластин здійснюється повне відбивання і жоден падаючий на поверхню дотику промінь не пройде в іншу пластину. Тому формальна відповідь

\(R\to\infty\).

 

Задача 16.5

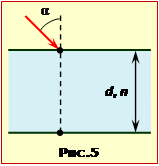Промінь світла падає під кутом \(\alpha=60^{\circ}\) на скляну (n = 1,5) плоскопаралельну пластину товщиною d = 3 см, що знаходиться в повітрі.

Визначити

зміщення x променя відносно його початкового напрямку після проходження крізь пластину.

Дано: \(\alpha\) = \(60^{\circ}\) n = 1,5 d = 3 см

x - ?

Розв’язання

Розглянемо хід променя крізь плоскопаралельну пластинку (рис.5-1) для цього запишемо закон заломлення світла (формула (16.6)), на верхній і на нижній гранях:

\(\frac{\sin\alpha}{\sin\beta}=n\),    \(\frac{\sin\beta}{\sin\alpha^{\prime}}=\frac{1}{n}\).

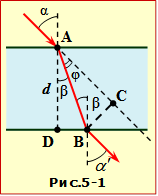
З цих виразів випливає, що \(\alpha^{\prime}=\alpha\). Це значить, що після проходження промінь не змінює напрямку, а тільки зміщується відносно падаючого на відстань x рівну довжині спільного перпендикуляра до цих променів: x = BC.

З прямокутного трикутника ABC:

\(x=\mathrm{AB}\cdot\sin\varphi=\mathrm{AB}\cdot\sin(\alpha-\beta)=\) \(=\mathrm{AB}(\sin\alpha\cos\beta-\sin\beta\cos\alpha)=\) \(=\mathrm{AB}\sin\alpha\cos\beta\left(1-\frac{\sin\beta}{\sin\alpha}\cdot\frac{\cos\alpha}{\cos\beta}\right)\),

(1)

де \(\beta\) – кут заломлення. За законом заломлення

\(\frac{\sin\alpha}{\sin\beta}=n\)    \(\Rightarrow\)     \(\sin\beta=\frac{\sin\alpha}{n}\),     \(\cos\beta=\sqrt{1-\sin^{2}\beta}=\sqrt{1-(\sin\alpha/n)^{2}}\).

(2)

З прямокутного трикутника AB:

\(\mathrm{AB}=\frac{\mathrm{AD}}{\cos\alpha}=\frac{d}{\cos\alpha }\).

(3)

Підставивши вирази (2) і (3) у формулу (1), після нескладних перетворень одержимо:

\(x=d\sin\alpha\left(1-\frac{\cos\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)\).

(4)

Виконаємо обчислення:

\(x=3\cdot\frac{\sqrt{3}}{2}\cdot\left(1-\frac{1/2}{\sqrt{1,5^{2}-3/4}}\right)=1,53\) см.

 

Задача 16.6

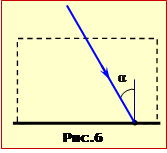Вузький паралельний пучок променів падає на аркуш паперу під кутом \(\alpha=60^{\circ}\) і створює світлову пляму (рис.6).

Визначити

відстань  S на яку зміститься цятка, якщо на папір покласти скляну (n = 1,5) пластину товщиною d = 5 см.

Дано: α = 60° n = 1,5 d = 5 см

S - ?

Розв’язання

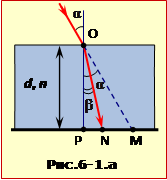Нехай спочатку світна цятка розміщена в точці M (рис.6-1.а). Після того як на папір поклали пластину, цятка внаслідок заломлення переміститься в точку N.

Шукана відстань S = MN. З рисунка видно, що

S = PM – PN = \(d(\mathrm{tg}\alpha-\mathrm{tg}\beta)\).

(1)

Величину \(\mathrm{tg}\beta\) легко визначити через відомі тригонометричні співвідношення та закон заломлення (16.6), згідно з яким \(\sin\beta=\sin\alpha/n\)

\(d(\mathrm{tg}\beta=\frac{\sin\beta}{\cos\beta}=\frac{\sin\beta}{\sqrt{1-\sin^{2}\beta}}=\frac{\sin\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\).

Підставивши цей вираз у формулу (1), дістанемо відповідь:

\(S=d\left(\mathrm{tg}\alpha-\frac{\sin\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)\).

Обчислення дають:

\(S=5\cdot\left(\sqrt{3}-\frac{\sqrt{3}}{2\cdot\sqrt{1,5^{2}-3/4}}\right)\approx\) 5,1 см.

Одержати відповідь у цій задачі також можна інакше.

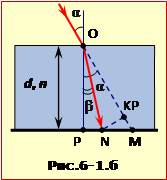Дійсно, якщо з точки N опустити перпендикуляр на лінію OM (рис. 16-1.б), то з трикутника NKM: NM = NK/\(\cos\alpha\). Відрізок NK = x був визначений у задачі 16.5 формула (4).

Отже маємо:

\(S=d\mathrm{tg}\alpha\left(1-\frac{\cos\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)=d\left(\mathrm{tg}\alpha-\frac{\sin\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)\).

 

Задача 16.7

Рибалка, що сидить у човні, розглядає камінчик на дні озера безпосередньо під човном. Рибалці здається, що камінчик знаходиться на глибині h = 3 м.

Визначити

істину глибину озера H. Показник заломлення води n = 1,33.

Дано: h = 3 м n = 1,33

H - ?

Розв’язання

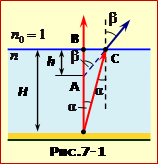Рибалка бачить камінчик завдяки тим відбитим від нього променям світла, що попадають в око. На рис.7-1 показані два таких промені, що виходять з точки розташування камінчика на дні A. Ці промені розходяться, тому рибалці буде здаватися, що вони виходять з точки A, розташованої на глибині h. Так виникає оптичний обман: удавана глибина водойми h виявляється меншою, ніж істинна глибина H.

Для розрахунків позначимо \(\alpha\) кут падіння променя на межу вода-повітря і \(\beta\) кут заломлення (рис.7-1). За законом заломлення (16.6)

де враховано, що показник заломлення повітря n₀ = 1. Трикутники ABC і A¢BC мають спільний катет BC, тому

Розв’язавши сумісно рівняння (1) і (2), одержимо:

З цього результату може здатися, що глибина озера H залежить від кута \)\alpha\). Звичайно це не так. Від кута \(\alpha\) залежить не H, а h, тобто положення точки A¢. Це означає, що продовження заломлених променів, що виходять з точки A під різними кутами, перетинаються в різних точках, і, отже, не створюють її зображення. Чому ж тоді ми чітко бачимо предмети на дні (звичайно, якщо вода прозора)? Відповідь така: тому що розміри зіниці дуже малі, в око попадають тільки промені, що виходять з води під дуже малими кутами (\(\alpha\ll{1}\)). У такому випадку величини \(\sin\alpha\) і \(n\sin\alpha\) у формулі (3) нехтовно малі і відповідь задачі фактично має вигляд:

\(H=nh=1,33\cdot{3}=4\) м.

Зверніть увагу на наступне. Подібна ситуація зустрічається в усіх задачах, зв'язаних з візуальними спостереженнями. Тому малість кутів необхідно враховувати із самого початку. Наприклад, у даній задачі необхідно було б одразу врахувати, що для малих кутів \(\sin\alpha=\mathrm{tg}\alpha=\alpha\) і записати закон заломлення у вигляді.

\(\frac{\alpha}{\beta}=\frac{1}{n}\).

Тоді відразу і набагато простіше була б отримана правильна відповідь:

\(\frac{H}{h}=n\)      \(\Rightarrow\)      \(H=nh\).

 

Задача 16.8

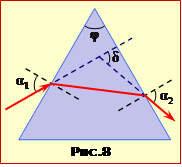Хід променя крізь скляну трикутну призму показаний на рис.8, на якому \(\alpha_{1}=30^{\circ}\), \(\alpha_{2}=60^{\circ}\), \(\delta=45^{\circ}\).

Визначити заломний кут призми \(\varphi\).

Дано: α1 = 30° α2 = 60° δ = 45°

φ - ?

Розв’язання

Позначимо кут заломлення на першій грані \(\beta_{1}\), а кут падіння на другу грань \(\beta_{2}\) (рис.8-1).

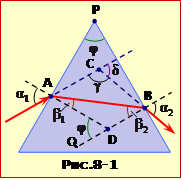Кут відхилення променя \(\delta\) – то є кут між напрямками променя, що вийшов з призми та променя, що падає на призму. Він є зовнішнім кутом трикутника ABC, отже

В цьому трикутнику \(\angle\)BAC = \(\alpha_{1}-\beta_{1}\) і \(\angle\)ABC = \(\alpha_{2}-\beta_{2}\). Тому

Прирівнюючи праві частини виразів (1) і (2), отримаємо:

Зовнішній кут \(\angle\)ADQ трикутника ABD дорівнює заломному кутові призми \(\varphi\), оскільки він утворений перпендикулярами до бічних граней призми. Отже

Підставивши цей вираз у формулу (3), дістанемо відповідь:

\(\delta=\alpha_{1}+\alpha_{2}-\varphi\)     \(\Rightarrow\)     \(\varphi=\alpha_{1}+\alpha_{2}-\delta=30^{\circ}+60^{\circ}-45^{\circ}\)

 

Задача 16.9

На бічну грань скляної (n = 1,5) призми, що має заломний кут \(\varphi=0,1\) рад, під малим кутом падає промінь світла.

Визначити кут відхилення \(\delta\) променя призмою.

Дано: φ = 0,1 рад n = 1,5

δ - ?

Розв’язання

Скористаємося результатами задачі 16.8 (формули (3) і (4)):

Відтак залишається визначити суму кутів \(\alpha_{1}\) та \(\alpha_{2}\). При малих кутах \(\sin\alpha\approx\alpha\), отже, за законом заломлення (16.6) можна наближено записати

де n – показник заломлення призми. Підставивши вирази (3) у формулу (1) і врахувавши співвідношення (2), отримаємо:

\(\delta=n(\beta_{1}+\beta_{2})-(\beta_{1}+\beta_{2})=(n-1)\varphi\).

Таким чином, при малих кутах падіння кут відхилення променя в призмі з малим заломним кутом залежить тільки від показника заломлення та заломного кута.

Виконаємо обчислення:

\(\delta=(1,5-1)\cdot{0,1}=0,05\) рад = \(2,86^{\circ}\).

 

Задача 16.10

Промінь світла падає на бічну грань тригранної скляної (n = 1,5) призми з кутом заломлення \(\varphi=60^{\circ}\).

Визначити

мінімальне значення кута падіння \(\alpha_{m}\), при якому світло буде проходити крізь призму.

Дано: n = 1,5 φ = 60°

αm - ?

Розв’язання

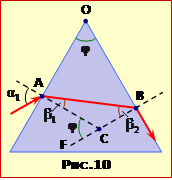На рис.10 показаний хід граничного променя крізь призму і відповідні кути.

Світло буде проходити крізь призму за умови

\(\beta_{2}\le\beta_{г}\),

(1)

де \(\beta_{г}\) – граничний кут, для якого відповідно до формули (16.7), умову (1) можна записати, як

\(\sin\beta_{2}\le\frac{1}{n}\).

З іншого боку (див. задачу 16.8, формула (4))

відповідно до цього світло проходить крізь призму за умови

\(\sin(\varphi-\beta_{1})\le\frac{1}{n}\).

З виразів (1) і (2) слідує, що найбільшій величині \(\beta_{1}=\beta_{г}\) відповідає таке значення \(\beta_{1}=\beta_{m}\), при якому

За законом заломлення (16.6) найменшому значенню \(\beta_{1}=\beta_{m}\) відповідає шуканий найменший кут падіння \(\alpha_{1}=\alpha_{m}\), причому

\(\sin\beta_{m}=\frac{\sin\alpha_{m}}{n}\).

Підставляючи цей вираз в рівність (3) і використовуючи відому тригонометричну формулу, одержимо

\(\frac{1}{n}=\sin\varphi\cdot\frac{1}{n}\sqrt{n^{2}-\sin^{2}\alpha_{m}}-\frac{1}{n}\sin\alpha_{m}\cos\varphi\)     \(\Rightarrow\)

\(\Rightarrow\)     \(1+\sin\alpha_{m}\cos\varphi=\sin\varphi\sqrt{n^{2}-\sin^{2}\alpha_{m}}\).

Зведемо останній вираз в квадрат і виконаємо перетворення:

\(\sin^{2}\alpha_{m}+2\sin\alpha_{m}\cos\varphi+1-n^{2}\sin^{2}\varphi=0\).

Рішення цього квадратного рівняння відносно \(\sin\alpha_{m}\)  дає

\(\sin\alpha_{m}=-\cos\varphi+\sqrt{\cos^{2}\varphi-1+n^{2}\sin\varphi}=-\cos\varphi+\sin\varphi\sqrt{n^{2}-1}\).

(Другий корінь не має фізичного змісту).

Виконаємо обчислення:

\(\sin\alpha{m}=-\cos{60^{\circ}}+\sin{60^{\circ}}\sqrt{1,5^{2}-1}\)     \(\Rightarrow\)      \(\alpha_{m}=27,9^{\circ}\).