ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
Розділ I. Геометрична оптика
1.3. Дзеркала і лінзи
|
На законах геометричної оптики ґрунтується дія різних оптичних приладів, які ”озброюють“ око. Їхніми основними функціональними елементами є дзеркала та лінзи, котрі створюють зображення на екрані, чи безпосередньо на сітківці ока. Строга теорія зображень є складною. Тому в елементарній оптиці світлові промені, що потрапляють на дзеркало чи лінзу, по замовчуванню вважаються параксіальними (такими, що падають в околі центра і під малим кутом). |
Дія оптичних пристроїв (ОП) ґрунтується на тому, що промені, котрі виходять з однієї точки S (рис. 16.4), після проходження крізь пристрій самі (рис. 16.4а), або їхні продовження (рис. 16.4б), збираються теж в одній точці S′, яка є зображенням точки S.
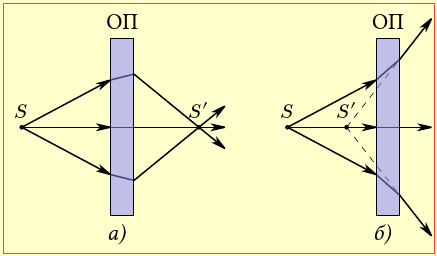
В першому випадку на поставленому в точці S′ екрані відбувається концентрація світлової енергії й утворюється дійсне зображення точки S. А в другому сходяться не самі промені, а їхні продовження, тож точка S′ є уявним зображенням точки S. Таке зображення можна побачити, пропустивши розбіжні промені, що пройшли, через додаткову збиральну лінзу, або, розглядаючи їх безпосередньо оком, кришталик якого править за додаткову лінзу, а сітківка – за екран.
Нагадаємо також, що створювані зображення, на загал, класифікують за такими ознаками:
- тип (дійсне чи уявне);
- розмір (збільшене або зменшене);
- орієнтація (пряме або перевернуте).
Далі розглядається утворення та характеристики зображень у найпростіших оптичних приладах, якими є плоскі та сферичні дзеркала й тонкі лінзи.
Плоске дзеркало. Це найпростіший оптичний прилад, що являє собою гладку плоску поверхню, котра повністю відбиває падаючі промені.
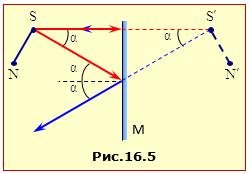
Рис. 16.5 ілюструє утворення зображення точки S і ”предмета“ SN у плоскому дзеркалі M. Ураховуючи закон відбивання (1.2) легко збагнути, що продовження відбитих дзеркалом променів, які вийшли з точки S, перетинаються в симетричній до неї точці \(S^{\prime}\). Те саме стосується й будь-якої іншої точки. Отже,
плоске дзеркало дає уявне пряме зображення предмета в натуральну величину,
котре відносно дзеркала є розташоване симетрично до самого предмета .
Сферичні дзеркала мають робочу поверхню у формі вгнутого, або опуклого сферичного сегмента (рис. 16.6) і характеризуються наступними геометричними параметрами:

- оптичний центр С – центр кривини робочої поверхні дзеркала;
- полюс O – вершина сферичного сегмента, що утворює дзеркало;
- головна оптична вісь CO – пряма, що проходить через центр і полюс дзеркала;
- побічна оптична вісь – будь-яка пряма, що проходить через оптичний центр дзеркала;
- фокус F – точка, в якій перетинаються відбиті промені у вгнутому та їхні продовження в опуклому дзеркалі при падінні паралельно до головної оптичній осі. Фокус знаходиться на головній оптичній осі й у вгнутому дзеркала є дійсний, а в опуклому – уявний.
- головна фокусна відстань F – відстань OF між полюсом і фокусом дзеркала – дорівнює половині радіуса кривини його поверхні:
|
|
\(F=\frac{R}{2}\) |
(1.5) |
- фокальна площина – площина, що проходить через фокус перпендикулярно до головної оптичної осі. Фокальна площина вгнутого дзеркала є дійсна, а опуклого – уявна.
Сферичне дзеркало є здатним до формування зображень, дякуючи наступній фокусувальній властивості:
|
будь-які паралельні між собою промені після відбивання від дзеркала самі, або їхні продовження перетинаються в одній точці фокальної площини. |
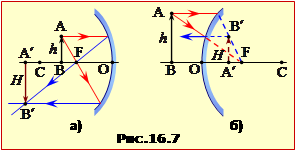
На рис. 16.7, відповідно до сказаного, наведено побудову зображення (стрілка A′B′) предмета (стрілка АВ) у вгнутому а) та опуклому б) дзеркалі, з якої можна встановити наступну формулу сферичного дзеркала:
|
|
\(\frac{1}{d}+\frac{1}{f}=\frac{1}{F}\), |
(1.6) |
де d = OA – відстань від предмета до дзеркала; f = OA′ – відстань від дзеркала до зображення; F = OF – головна фокусна відстань дзеркала. Ця формула охоплює всі можливі ситуації, якщо величини d, f, F розглядати як алгебраїчні у відповідності з наступним правилом знаків:
|
відстань між полюсом дзеркала і дійсною точкою береться зі знаком "+", а між полюсом і уявною точкою – зі знаком "–". |
(Нагадаємо, що в дійсних точках сходяться самі промені, а в уявних – їхні продовження).
Висота зображення H = A′B′ при заданій висоті предмета h = AB визначається поперечним збільшенням Г = (H/h), котре, як видно з рис. 16.7, складає
|
$\Gamma =\frac{f}{d}$. |
(1.7) |
Величина f задовольняє формулу (1.6), тож після елементарних перетворень отримаємо вираз
|
|
\(\Gamma=\frac{F}{d-F}\), |
(1.7а) |
в якому знак Г визначає тип зображення – при Г > 0 воно є дійсне, а при Г < 0 – уявне.
У вгнутому дзеркалі (F > 0) можливі різні випадки, а саме.
1. d > 2F : 0 < Г < 1 — зображення дійсне зменшене;
2. d = 2F : Г = 1 — зображення дійсне в натуральну величину;
3. F < d < 2F: Г > 1 — зображення дійсне збільшене;
4. d < F : Г < 1, — зображення уявне зменшене;
5. d = F: \(\Gamma\to\infty\) і, відповідно до формули (1.7), \(f\to\infty\). Це означає, що відбиті промені ніде не перетинаються, й зображення не існує.
Сферичні лінзи являють собою прозорі тіла з двома сферичними поверхнями. (Одна з поверхонь може бути й плоскою). На рис.16.8 показано в розрізі різні типи лінз: двоопукла (а), плоско-опукла (б), двовгнута (в), плоско-вгнута (г), опукло-вгнута, інакше меніск (д, е).
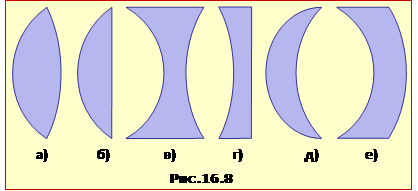
За дією на світлові пучки лінзи є подібні до дзеркал із тією відміною, що формують пучки не відбитих променів, а тих, що проходять крізь лінзу. Зокрема, лінзи теж поділяються на збиральні та розсіювальні. Перші перетворюють паралельний пучок променів на збіжний, а другі – на розбіжний. При цьому дія лінзи на хід променів визначається кривиною поверхонь і співвідношенням показників заломлення речовини лінзи та навколишнього середовища. До прикладу, у повітрі лінзи з профілем а), б), є збиральними, а типів в), г), – розсіювальними. Що до менісків, то їхня фокусувальна дія залежить від співвідношення кривин поверхонь, так на рис. 16.8 меніск д) є збиральним, а е) — розсіювальним.
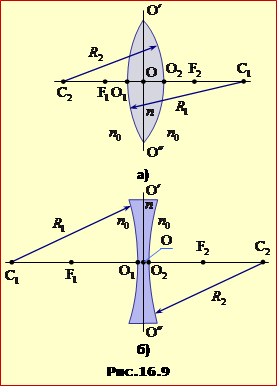 Для ілюстрації та кількісної характеристики впливу лінзи на світлові промені використовують наступні геометричні параметри (рис.16.9):
Для ілюстрації та кількісної характеристики впливу лінзи на світлові промені використовують наступні геометричні параметри (рис.16.9):
- радіуси кривини R1, R2 поверхонь;
- головна оптична вісь C1C2 – пряма, що проходить через центри кривини поверхонь;
- у тонкій лінзі можна вважати, що полюси O1 і O2 сферичних сегментів розташовані практично в одній точці O, що називається оптичним центром лінзи;
- побічна вісь – будь-яка пряма, що проходить через оптичний центр лінзи;
- площина лінзи O′O″ – площина, що проходить через оптичний центр лінзи перпендикулярно до головної оптичній осі;
- фокуси F1, F2 – точки на головній оптичній осі, у яких перетинаються заломлені промені (збиральна) або їхні продовження (розсіювальна лінза), котрі падають на лінзу паралельно до головної оптичної осі. У збиральній лінзі фокуси є дійсні, а в розсіювальній – уявні. Крім того можна вважати, що в тонкій лінзі фокуси розташовані на однаковій відстані від оптичного центра;
- фокусна відстань F = OF1 = OF2 – відстань між фокусом і оптичним центром лінзи;
- оптична сила лінзи D – величина, обернена до фокусній відстані:
|
|
\(D=\frac{1}{ F}\). |
(1.8) |
Оптична сила вимірюється в діоптріях (дптр): 1 дптр = 1 м–1 – це оптична сила лінзи з фокусною відстанню 1 м. Для збиральної лінзи оптична сила D > 0, для рзсювальної D < 0 і визначається формулою:.
|
|
\(D=\left(\frac{n}{n_{0}}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\). |
(1.9) |
де n, n0 – показники заломлення речовини лінзи та навколишнього середовища; R1, R2, – відповідно, радіуси кривини передньої та задньої відносно падаючого променя поверхні лінзи. При цьому величини R1, R2 розглядаються як алгебраїчні: радіус опуклої поверхні береться зі знаком "+", а вгнутої – зі знаком "–".
Зазвичай середовищем є повітря. В такому разі
|
\(D=\left({n}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\). |
(1.9а) |
- фокальна площина – площина, що проходить через фокус перпендикулярно до головної оптичної осі. Фокальна площина збиральної лінзи є дійсною, а розсіювальної – уявною й має наступну збиральну властивість:
|
будь–які паралельні між собою промені після проходження крізь лінзу перетинаються (самі або їхні продовження) в одній точці фокальної площини. |
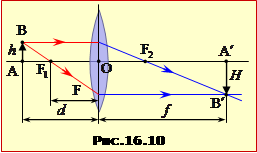
Розташування предмета AB та його зображення A′B′ у лінзі (рис. 16.10) є пов'язані формулою тонкої лінзи:
|
|
\(\frac{1}{d}+\frac{1}{f}=\frac{1}{F}\), |
(1.10) |
що по формі й суті збігається з формулою сферичного дзеркала (1.6) із таким самим правилом знаків.
Те саме стосується й формул поперечного збільшення:
|
|
\(\Gamma=\frac{f}{d}\), |
(1.11) |
|
|
\(\Gamma=\frac{F}{d-F}\). |
(1.11а) |
Формули (1.10), (1.11), (1.11а) та (1.6), (1.7) і (1.7a) є ідентичні. Це означає, що проведений для дзеркал аналіз зображень і встановлені співвідношення є чинними й для тонких лінз.
На завершення зауважимо, що на практиці в різних оптичних приладах часто використовують не поодинокі лінзи, а системи, з яких найпростішою є дві тонкі лінзи із спільною головною оптичною віссю. Зокрема, такою є око людини, "озброєне" окулярами.
Оптична сила системи лінз, розташованих впритул одна до одної, дорівнює алгебраїчній сумі оптичних сил з'єднаних лінз. Для двох лінз
|
|
D = D1 + D2. |
(1.12) |