ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
Розділ I. Геометрична оптика
1.2. Закони відбивання і заломлення
|
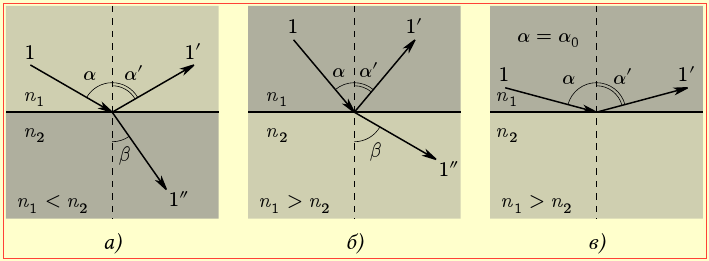
В однорідних ізотропних середовищах напрямки падаючого (1), відбитого (1′) і заломленого (1″) променів (рис. 16.2) пов'язані наступними законами. |
|
$\frac{\sin \alpha }{\sin \beta }=\frac{{{n}_{2}}}{{{n}_{1}}}$ або \(n_{1}\sin\alpha=n_{2}\sin\beta\) |
(1.3) |
Зауваження. В багатьох задачах на заломлення світла йдеться про візуальні спостереження. В такому разі, через малі розміри зіниці ока, слід використовувати наближення $\sin \alpha =\operatorname{tg}\alpha =\alpha $ і записувати закон заломлення у вигляді:
| \(\frac{\alpha}{\beta}=\frac{n_{2}} {n_{1}}\) або \(n_{1}\alpha=n_{2}\beta\). |
(1.3а) |
Із співвідношення (1.3) випливає, що при переході світла із оптично менш густого (n1 < n2) середовища в більш густе (рис.16.2а) заломлений промінь відхиляється в напрямку нормалі до межі поділу середовищ, а у випадку n1 > n2 (рис.16.2б) — від неї. В останньому випадку поступовому збільшенні кута падіння до деякій величині \(\alpha_{0}\) кут заломлення набуває максимально можливого значення \(90^{\circ}\) (рис.16.3). Відповідно, величина \(\alpha_{0}\) називається граничним кутом для даних двох середовищ і за законом (1.3), визначається співвідношенням
|
|
\(\sin\alpha_{0}=\frac{n_{2}}{n_{1}}\), \(n_{1}\gt{n}_{2}\). |
(1.4) |
Теорія й практика свідчать, що за вказаних умов при поступовому збільшенні кута падіння до величини \(\alpha_{0}\) інтенсивність заломленого променя зменшується до нуля, а відбитого променя збільшується від нуля до інтенсивності падаючого. Це означає, що при падінні з оптично більш густого середовища на межу з менш густи під кутом \(\alpha\ge\alpha_{0}\) світло далі не проходить, тобто відбувається повне внутрішнє відбивання. Прикладом цього, зокрема, є всім знайоме сліпуче виблискування на сонці дощових крапель на траві.