ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
1. Теоретичні відомості.
1.1. Рівняння і параметри монохроматичної хвилі
|
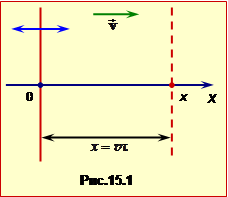
Аби з’ясувати, як і від чого залежать властивості монохроматичної хвилі, уявімо нескінченну площину-мембрану, що починає здіснювати гармонічні коливання в однорідному пружному середовищі вздовж осі ОХ, як показано на схематичному рис. 15.1. Залежність $\text{ }\!\!\xi\!\!\text{ }\left( x,t \right)$ легко встановити. Справді, нехай коливання мембрани та прилеглих (x = 0) шарів середовища відбуваються з амплітудою А і періодом за законом |
|
|
|
$\text{ }\!\!\xi\!\!\text{ }\left( 0,t \right)=A\cos \frac{2\text{ }\!\!\pi\!\!\text{ }}{T}t.$ |
|
|
(Примітка. З таким самим успіхом можна використати й функцю sin)
Тоді, врахувавши, що при швидкості поширення хвилі v коливання на відстані x від мембрани почнуться пізнше на час $\tau =(x/v)$, отримаємо наступне рівняння плоскої монохроматичної хвилі:
|
$\text{ }\!\!\xi\!\!\text{ }\left( x,t \right)=A\cos \frac{2\text{ }\!\!\pi\!\!\text{ }}{T}\left( t-\frac{x}{v} \right),$ |
(3.1) |
або через частоти:
|
$\text{ }\!\!\xi\!\!\text{ }\left( x,t \right)=A\cos 2\pi \nu \left( t-\frac{x}{v} \right),$ |
(3.1а) |
|
$\text{ }\!\!\xi\!\!\text{ }\left( x,t \right)=A\cos \omega \left( t-\frac{x}{v} \right).$ |
(3.1б) |
Одразу слід зауважити, що коливаня в хвилі є вимушеними, тож їхнї параметри задаються джерелом. Отже,
|
амплітуда і період, (або циклічна чи лінійна частоти) хвилі не залежать від властивостей середовища. |
Натомість
|
швидкість поширення хвилі визначається тільки її фізичною природою та властивостями середовища |
Як видно з рівнянь (3.1), на заданій відстані від джерела x = x0 шар молекул здійснює коливання за законом
|
$\text{ }\!\!\xi\!\!\text{ }\left( t \right)=A\cos \left( \frac{2\text{ }\!\!\pi\!\!\text{ }}{T}t-{{\text{ }\!\!\varphi\!\!\text{ }}_{0}} \right),$ |
(3.2) |
з періодом T, амплітудою A (рис.15.2а відмітити А) і початковою фазою
|
${{\text{ }\!\!\varphi\!\!\text{ }}_{0}}=\frac{2\text{ }\!\!\pi\!\!\text{ }{{x}_{0}}}{vT}\text{.}$ |
(3.2а). |
Аналогічно розподіляються в просторі й відхилення $\text{ }\!\!\xi\!\!\text{ }$(x) шару молекул від положення рівноваги (рис.15.2б) в будь-який заданий момент часу $t={{t}_{0}}$:
| \(\xi(x)=A\cos\left(\frac{2\pi}{Tv}x-\varphi_{0}^{\prime}\right)\), | (3.3) |
де
|
\(\varphi_{0}^{\prime}=\frac{2\pi{t}_{0}}{T}\). |
(3.3а) |
При цьому значення $\text{ }\!\!\xi\!\!\text{ }$ періодично повторюються в напрямку поширення хвилі на відстані, яка називається довжиною хвилі $\lambda $. Тож, відповідно до рівняння (3.3),
|
$\frac{2\pi }{vT}\left( x+\lambda \right)-\frac{2\pi }{vT}x=2\pi \quad \Rightarrow \quad \lambda =vT$, |
(3.4) |
тобто,
довжина хвилі – це відстань, на яку хвиля поширюється за один період коливань.
При цьому
|
довжина хвилі залежить і від джерела, що задає період коливань, і від середовища, котре визначає швидкість їхнього поширення. |
Довжину хвилі можна виразити також через частоту:
|
$\lambda =\frac{v}{\nu },$ або $\lambda =\frac{2\text{ }\!\!\pi\!\!\text{ }v}{\omega }.$ |
(3.4а) |
Використання параметра λ надає рівнянню (3.1) вигляду:
|
$\text{ }\!\!\xi\!\!\text{ }\left( x,t \right)=A\cos \left( \frac{2\text{ }\!\!\pi\!\!\text{ }}{T}t-\frac{2\text{ }\!\!\pi\!\!\text{ }}{\lambda }x \right)$, |
(3.5) |
який ’’симетрично’’ відображує періодичність хвильового процесу і в часі, і в просторі і є одним із головних параметрів хвилі. Але в теорії замість довжини хвилі зазвичай використовують хвильове число
|
$k=\frac{2\text{ }\!\!\pi\!\!\text{ }}{\lambda }$, |
(3.6) |
що, з урахуванням співвідношення T = (2π/ω), дозволяє найбільш компактно й зручно для викладок записати рівняння (3.5), як
|
$\text{ }\!\!\xi\!\!\text{ }\left( x,t \right)=A\cos \left( \omega t-kx \right).$ |
(3.7) |
Загальні результати, котрі отримано тут для плоскої хвилі, зберігають чинність і для інших типів хвиль, зокрема, сферичних хвиль, які збуджуються точковим джерелом (маленькою вібруючою кулькою) в однорідному ізотропному середовищі. Але, на відміну від плоскої, у сферичній хвилі енергія переноситься не в один бік, а радіально по всіх напрямах від місця розташування джерела. Через це кожна випромінена порція енергії поступово розподіляється по все більшій поверхні, через що амплітуда хвилі в напрямку поширення зменшується пропорційно відстані r до джерела. Отож, рівняння сферичної хвилі має вигляд:
|
$\text{ }\!\!\xi\!\!\text{ }\left( r,t \right)=\frac{A}{r}\cos \left( \omega t-kr \right)$, А = const. |
(3.7а) |
Поширення коливань зумовлює перенесення хвилею енергії, тож і її дію на об'єкти, що перебувають у хвильовому полі. Кількісною мірою перенесення енергії є
інтенсивність хвилі – енергія, що переноситься за одиницю часу через одиницю площі хвильової поверхні, що проходить через дану точку:
|
$I=\frac{\Delta W}{\Delta t\Delta S}$ (Вт/м2) |
(3.8) |