ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
| Site: | physics.zfftt.kpi.ua |
| Course: | physics.zfftt.kpi.ua |
| Book: | ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс |
| Printed by: | |
| Date: | Saturday, 28 February 2026, 9:16 AM |
Table of contents
- КОЛИВАННЯ І ХВИЛІ. ВСТУП
- Розділ І. Механічні коливання
- 1.Теоретичні відомості.
- 2. Приклади розв’язування задач
- 3. Задачі для самостійної роботи
- Розділ ІІ. Електромагнітні коливання. Змінний струм
- 1. Теоретичні відомості
- 2. Приклади розв'язування задач
- 3. Задачі для самостійної роботи
- Розділ ІІІ. Хвилі
- 1. Теоретичні відомості.
- 2. Приклади розв'язування задач
- 3. Задачі для самостійної роботи
КОЛИВАННЯ І ХВИЛІ. ВСТУП
Коливаннями називають фізичні процеси, що в тій або іншій мірі регулярно повторюються з часом. Наочним прикладом можуть слугувати механічні коливання – такі рухи тіла, при яких напрям, швидкість та інші характеристики руху багаторазово змінюються на протилежні. У речовині частинки пов'язані між собою. Тому будь-яке збурення[1], створене в одному місці, передається до сусідніх частинок, від них – до їхніх "сусідів" і т.д. У результаті виникає хвиля – поширення збурень у просторі з плином часу. Примітка. Збуреннями називають різкі відхилення характеристик середовища від їхніх рівноважних значень. Коливання і хвилі можуть мати як механічну, так і електромагнітну природу. Але ті й інші мають однакові загальні властивості й описуються математично ідентичними загальними рівняннями і формулами. Тому фізика коливань і хвиль утворює окремий розділ фізичної науки. Далі розглянуто: |
Розділ І. Механічні коливання
Найзручнішими для вивчення є
|
гармонічні коливання – процеси, що визначаються гармонічними функціями синус, або косинус. Гармонічні коливання мають широке практичне застосування, а в теорії складають базу для вивчення більш складних коливальних процесів. Даний розділ присвячено механічним гармонічним коливанням, при яких гармонічними функціями визначаються параметри руху тіла. Далі розглянуто: 1. Теоретичні відомості 2. Приклади розв’язування задач 3. Задачі для самостійної роботи |
1.Теоретичні відомості.
Основні властивості механічних гармонічних коливань розглянуто в наступнх питаннях:
1.1. Рівняння координати та параметри гармонічних коливань
Визначальною рисою механічних гармонічних коливань є те, що вони відбуваються в обмеженій області простору й характеризуються строгою повторюваністю. Це відображує наступне рівняння координати при гармонічних коливаннях точки:
|
|
\(x={{x}_{m}}\cos \left( \frac{2\pi }{T}t+{{\varphi }_{0}} \right)\), |
(1.1) |
або
|
|
$x={{x}_{m}}\sin \left( \frac{2\pi }{T}t+{{\varphi }_{0}}^{\prime } \right)$, |
(1.1а) |
де \(\varphi_{0}^{\prime}=\varphi_{0}+\pi/2\).
Постійні величини xm, T, \(\varphi_{0}\) є параметрами – кількісними характеристиками – коливань і називаються, відповідно, амплітудою, періодом і фазою. Їхній зміст наочно ілюструє рис. 1.1
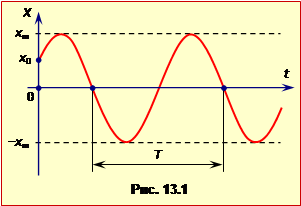
Амплітуда xm (її також часто позначають як А) – то є максимальне зміщення точки з положення рівноваги. Вона визначає "розмах" коливань: усі можливі значення координати коливної точки лежать в інтервалі \(\left[-x_{m},\ x_{m}\right]\).
Період T – це проміжок часу, протягом якого відбувається одне повне коливання, тобто час, через який рух точки в точності повторюється.
Періодичність руху при коливаннях характеризують також лінійною ν та циклічною (коловою) ω частотою.
Линійна частота дорівнює кількості коливань, що відбуваються за 1 с:
|
|
\(\nu=\frac{1}{T}\), |
(1.2) |
і вимірюється у герцах (Гц). 1 Гц = 1 с−1 – частота, при якій за 1 с відбувається одне коливання. При високих частотах використовують кілогерци (1 кГц = 103 Гц) і мегагерци (1 МГц = 106 Гц).
Циклічна (колова) частота є пов'язана з періодом і лінійною співвідношеннями:
|
|
\(\omega=\frac{2\pi}{T}=2\pi\nu\). |
(1.3) |
Циклічна частота вимірюється у радіанах за секунду (рад/с, або 1/с).
Використовуючи співвідношення (1.3), рівняння гармонічних коливань (1.1) можна записати через частоту:
|
|
\(x=x_{m}\cos(\omega{t}+\varphi_{0})\), |
(1.4) |
або
|
|
\(x=x_{m}\cos(2\pi\nu{t}+\varphi_{0})\) |
(1.4а) |
Фазою \(\varphi\) називається значення аргументу тригонометричної функції в наведених рівняннях:
\(\varphi=\frac{2\pi}{T}t+\varphi_{0}=\omega{t}+\varphi_{0}=2\pi\nu{t}+\varphi_{0}\).
Відповідно, величина ${{\varphi }_{0}}=\varphi \left( 0 \right)$ є початковою фазою коливань. Вона залежить від вибору моменту початку відліку часу й може мати будь-яке значення в інтервалі від 0 до \(2\pi\) рад.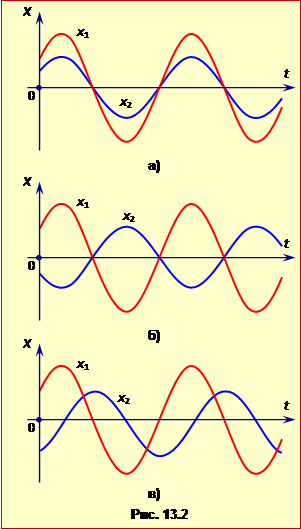
Фаза визначає поточний стан коливного тіла. Відповідно, різниця фаз \(\delta=\varphi_{01}-\varphi_{02}\) визначає узгодженість у часі коливань із однаковою частотою. Якщо різниця фаз \(\delta=0\) (рис.1.2а), то говорять, що коливання відбуваються "у фазі" або ''синфазно'', а при \(\delta=\pi\) (рис.1.2б) – "у протилежних фазах" або "в протифазі". В інших випадках говорять, що коливання відбуваються із "зсувом фаз" \(\delta\) (до прикладу, на рис.1.2б зсув фаз складає \(\pi\), а на рис.1.2в \(\delta=\frac{\pi}{2}\)).
1.2. Швидкість, прискорення і сила при гармонічних коливаннях
Рівняння швидкості точки при гармонічних коливаннях одержимо, взявши першу похідну по часу від координати (рівняння (1.4)):
|
|
\(v_{x}=x^{\prime}(t)=-\omega{x}_{m}\sin(\omega{t}+\varphi_{0})\), |
(1.5) |
або
|
|
\(v_{x}=v_{m}\cos\left(\omega{t}+\varphi_{0}+\frac{\pi}{2}\right)\), |
(1.5a) |
де vm – амплітуда швидкості, що пов'язана з амплітудою зміщення xm співвідношенням
|
|
\(v_{m}=\omega{x}_{m}\). |
(1.6) |
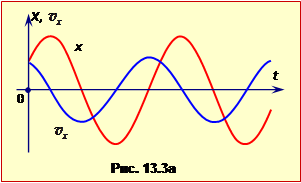
Порівнюючи рівняння (1.4) і (1.5), бачимо, що коливання швидкості за фазою випереджають коливання координати точки на \(\pi/2\) або на чверть періоду (рис.1.3а).
Рівняння прискорення одержимо, визначивши похідну швидкості з рівняння (1.5):
|
|
\(a_{x}=v_{x}^{\prime}=-\omega^{2}x_{m}\cos(\omega{t}+\varphi_{0})\) |
|
або
|
|
\(a_{x}=a_{m}\cos(\omega{t}+\varphi_{0}+\pi)\), |
(1.7) |
де величина
|
\(a_{m}=\omega^{2}x_{m}\), |
(1.8) |
|||
є амплітудою прискорення, котру, згідно з виразом (1.6), можна подати й так:
|
\(a_{m}=\omega{v}_{m}\). |
(1.8а) |
|||
З рівняння (1.7) видно, що коливання прискорення відбуваються з різницею фаз \(\pi\), тобто в протифазі до коливань координати (рис.1.3б).
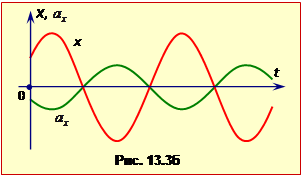
Слід зауважити, що тригонометрична функція в рівняннях швидкості й прискорення є визначена неоднозначно і залежить від вигляду цієї функції в рівнянні зміщення. До прикладу, при використанні рівняння (1.1a) у рівнянні (1.5) буде фігурувати функція \(\cos\), а в рівнянні (1.6) – функція \(\sin\). Але будь-що,
|
|
\(a_{x}=-\omega^{2}{x}\), |
(1.9) |
тобто,
|
при гармонічних коливаннях прискорення точки в будь-який момент є прямо пропорційне до її зміщення з положення рівноваги й напрямлене до нього. |
Відповідно до другого закону Ньютона та рівняння (1.9), прикладена до коливної точки рівнодійна сила у будь-який момент часу визначається, як
|
|
\(F_{x}=-kx\), |
(1.10) |
де
|
|
\(k=m\omega^{2}\). |
(1.11) |
Формула виражає критерій гармонічності механічних коливань:
|
якщо рівнодійна сил, які діють на матеріальну точку, є прямо пропорційною до зміщення з положення рівноваги й і спрямована до нього, то точка здійснює гармонічні коливання. |
При цьому частота і період гармонічних коливань визначаються наступними загальними формулами:
|
|
\(\omega=\sqrt{\frac{k}{m}}\). |
(1.12) |
||
|
|
\(\nu=\frac{1}{2\pi}\sqrt{\frac{k}{m}}\). |
(1.12а) |
||
|
|
\(T=2\pi\sqrt{\frac{m}{k}}\), |
(1.13) |
||
де m – маса матеріальної точки, що коливається, k – коефіцієнт пропорційності між рівнодійною силою і відхиленням точки від положення рівноваги.
1.3. Маятники.
Маятниками називають тіла, здатні здійснювати вільні коливання навколо фіксованого положення рівноваги. Найпростішими серед них є пружинний та математичний маятники.
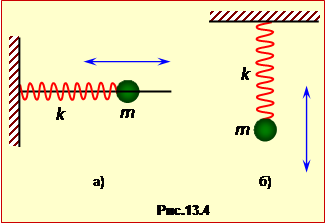
Пружинний маятник являє собою тіло маси m, з'єднане з невагомою пружиною жорсткістю k із закріпленим іншим кінцем (рис.1.4).
За відсутності сил тертя та опору повітря (на практиці – коли ними можна нехтувати), рух маятника визначається тільки силою пружності ([І], розділ V) у деформованій пружині, котра задовольняє умову (1.10)
\(F=-kx\),
де x – величина деформації.
Отже,
пружинний маятник здійснює гармонічні коливання з циклічною частотою
|
|
\(\omega=\sqrt{\frac{k}{m}}\) |
(1.14) |
і періодом
|
|
\(T=2\pi\sqrt{\frac{m}{k}}\), |
(1.15) |
де m – маса маятника, k – жорсткість пружини.
Все сказане стосується як горизонтальних (рис.1.4а), так і вертикальних (рис.1.4б) коливань, але в останньому випадку величина x не включає статичну деформацюю пружини маятника під дією сили тяжіння.
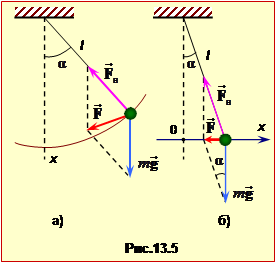 Математичний маятник являє собою тіло маси m на невагомому нерозтяжному підвісі довжиною l із закріпленим кінцем (рис. 1.5).
Математичний маятник являє собою тіло маси m на невагомому нерозтяжному підвісі довжиною l із закріпленим кінцем (рис. 1.5).
За відсутності сил тертя в підвісі та опору середовища рух маятника відбувається під дією сил тяжіння \(m\vec{g}\) і натягу підвісу \(\vec{F}_{н}\), рівнодійна яких
\(\vec{F}=m\vec{g}+\vec{F}_{н}\)
при значних відхиленнях маятника (рис.1.5а) складно залежить від кута \(\alpha\). Тому довільні коливання математичного маятника не є гармонічними. Одначе при малих амплітудах ситуація спрощується, бо при \(\alpha\ll{1}\) \(\mathrm{tg}\alpha=\sin\alpha=\alpha\). Отже, можна вважати, що малі коливання математичного маятника відбуваються вздовж горизонтальної осі ОХ (рис.1.5б) під дією повертаючої сили
\(F_{x}=-mg\cdot\mathrm{tg}\alpha=-mg\alpha\).
З тієї ж причини можна прийняти, що в будь-який момент часу кут відхилення маятника від положення рівноваги α = (x/l). У такому разі
\(F_{x}=-kx\),
де x – зміщення маятника з положення рівноваги і
|
|
\(k=\frac{mg}{l}\), |
(1.16) |
Отже, згідно з критерієм (1.10),
|
малі вільні коливання математичного маятника є гармонічними. |
Зіставивши вираз (1.16) з формулами (1.12) та (1.13), дісттанемо наступні формули для циклічної частоти \(\omega\) та періоду T коливань математичного маятника:
|
|
\(\omega=\sqrt{\frac{g}{l}}\); |
(1.17) |
|
|
\(T=2\pi\sqrt{\frac{l}{g}}\). |
(1.18) |
1.4. Енергія гармонічних коливань
|
|
\(W_{п}=\frac{kx^{2}}{2}\). |
(1.19) |
Отже згідно з рівнянням (1.1), в будь-який момент часу вона дорвнює
|
|
\(W_{п}=\frac{kx_{m}^{2}}{2}\cos^{2}(\omega{t}+\varphi_{0})\), |
(1.19a) |
де k – жорсткість пружини, xm – амплітуда коливань.
Формула (1.19) зберігає чинність і для математичного маятника, де потенціальна енергія коливань визначається роботою проти рівнодійної сил тяжіння та натягу підвісу при відхиленні маятника від положення рівноваги. При цьому величина k визначається виразом (1.16):
\(k=\frac{mg}{l}\).
Кінетична енергія гармонічних коливань
|
|
\(W_{к}=\frac{mv^{2}}{2}\) |
|
у відповідності до рівняння (1.5) виражається як
|
|
\(W_{к}=\frac{mv_{m}^{2}}{2}\sin^{2}(\omega{t}+\varphi_{0})\), |
(1.20) |
де m – маса, vm – амплітуда швидкості тіла.
Якщо за допомогою співвідношень (1.5б) і (1.11) максимальну потенціальну енергію у рівнянні (1.19а) і максимальну кінетичну енергію у рівнянні (1.20) виразити через масу тіла m та частоту \(\omega\) й амплітуду коливань xm, то вийде:
|
|
\(\frac{mv_{m}^{2}}{2}=\frac{kx_{m}^{2}}{2}=\frac{m\omega^{2}x_{m}^{2}}{2}=W_{0}\). |
|
З урахуванням цього повна енергія гармонічних коливань у будь-який момент часу
\(W=W_{к}+W_{п}=W_{0}\left(\cos^{2}(\omega{t}+\varphi_{0})+\sin^{2}(\omega{t}+\varphi_{0})\right)=W_{0}\).
Отже, як і говорилося напочатку,
|
повна енергія гармонічних коливань зберігається: |
|||
|
|
\(W_{п}+W_{к}=\) const. |
|
|
Цей результат має просте пояснення: гармонічні коливання можливі тільки тоді, коли відсутні сили тертя й опору, тобто не відбувається перетворення механічної енергії на інші види.
1.5. Диференціальне рівняння вільних гармонічних коливань
Якщо у рівнянні (1.7) величину ax представити у вигляді другої похідної координати по часу (див. [І], ф-ли (1.8)), то одержимо диференціальне рівняння гармонічних коливань:
|
|
\(x^{\prime\prime}=-\omega^{2}x\). |
(1.21) |
(Примітка. Диференціальним називається рівняння, до якого, крім шуканої функції, входять її похідні).
У математиці доводиться, що єдиними можливими розв'яками рівняння (1.21) є функції sin або cos. При цьому фізична природа величини x не має значення. До прикладу, для математичного маятника роль x відіграє кут відхилення нитки від вертикалі, а при розгляді електромагнітних коливань у коливальному контурі – заряд конденсатора, або сила струму в котушці, тощо.
Рівняння (1.21) виражає загальну ознаку гармонічних коливань:
|
якщо друга похідна по часу деякої фізичної величини є прямо пропорційна до самої величини й має протилежний знак, то ця величина здійснює гармонічні коливання, частота яких визначається коефіцієнтом пропорційності між нею та її другою похідною. |
2. Приклади розв’язування задач
При розгляді задач на коливання, як і в теорії, не враховуються сили тертя та опору повітря.
Далі наведено приклади розв'язування задач із наступних тем:
2.1. Рівняння і характеристики гармонічних коливань
У задачах, де потрібно складати рівняння гармонічних коливань за заданими характеристиками і початковими умовами, іноді виникають проблеми з визначенням початкової фази. Тож необхідно пам'ятати, що для її визначення треба використовувати обидві початкові умови (x(0), v(0)), бо тільки однією початкова фаза визначається неоднозначно.
Для визначення характеристик гармонічних коливань за заданим рівнянням слід записати його числовому вигляді й, порвнюючи з відповідним рівнянням із теорії, встановити значення шукаих величин. При цьому слід пам'ятати, що коли в умові не вказано одиниці вимірювання, то значення величин по замовчуванню подано в основних одиницях СІ.
Задача 1.1. Точка здійснює гармонічні коливання з періодом T = 1,57 c і амплітудою A = 12 см. Записати рівняння руху точки x(t), якщо в початковий момент часу вона має координату x0 = 6 см і віддаляється від положення рівноваги.
Задача 1.2. Точка здійснює гармонічні коливання так, що на відстанях x1 = 3 см і x2 = 5 см від положення рівноваги її швидкість становить v1 = 10 см/с і v2 = 6 см/с, відповідно. Визначити циклічну частоту \(\omega\) й амплітуду A коливань точки.
Задача 1.3. Визначити середню шляхову швидкість \(\langle{v}\rangle\) тіла, що здійснює гармонічні коливання, якщо його максимальна швидкість складає \(v_{m}\) = 10 м/с.
Задача 1.1
Точка здійснює гармонічні коливання з періодом T = 1,57 c і амплітудою A = 12 см.
Записати
рівняння руху точки x(t), якщо в початковий момент часу вона має координату x0 = 6 см і віддаляється від положення рівноваги.
|
Дано: T = 1,57 c
A = 12 см
\(x_{0}\) = 6 см
|
|
x(t) - ?
|
Розв’язання
Оскільки в початковий момент часу ні координата, ні швидкість точки не дорівнюють нулю, то немає значення, яку функцію вибрати для опису коливань. Отож будемо шукати рівняння x(t) у вигляді
|
|
\(x(t)=A\cos\left(\frac{2\pi}{T}t+\varphi_{0}\right)\). |
(1) |
Значення A і T задані, отже, задача зводиться до визначення початкової фази \(\varphi_{0}\). Підставивши в рівняння (1) значення t = 0, x0 і A, одержимо
\(6=12\cos\varphi_{0}\) \(\Rightarrow\) \(\cos\varphi_{0}=\frac{1}{2}\) \(\Rightarrow\) \(\varphi_{0}=\pm\frac{\pi}{3}\).
Для вибору знаку \(\varphi_{0}\) врахуємо, що за умовою у початковий момент напрям швидкості точки збігається з напрямом осі OX, тобто \(v_{0x}>0\). Проекція швидкості \(v_{0x}=x^{\prime}(t)\), тому відповідно до рівняння (1) отримаємо
\(v_{x}=x^{\prime}(t)=-A\frac{2\pi}{T}\cos\left(\frac{2\pi}{T}\cdot{t}+\varphi_{0}\right)\).
При t = 0
\(v_{0x}=-A\frac{2\pi}{T}\sin\varphi_{0}\).
Оскільки \(v_{0x}>0\), то
\(\sin\varphi_{0}<0\) \(\Rightarrow\) \(\varphi_{0}<0\).
Отже, початкова фаза \(\varphi_{0}=-\pi/3\).
Підставивши в рівняння (1) всі числові значення, отримаємо відповідь:
\(x(t)=12\cos\left(4t-\pi/3\right)\), см.
Зауваження. Зверніть увагу на те, що при складанні рівняння коливань у відповіді всі величини, окрім часу, повинні бути представлені в числовому вигляді.
Задача 1.2
Точка здійснює гармонічні коливання так, що на відстанях x1 = 3 см і x2 = 5 см від положення рівноваги її швидкість становить v1 = 10 см/с і v2 = 6 см/с, відповідно.
Визначити
циклічну частоту \(\omega\) й амплітуду A коливань точки.
|
Дано: \(x_{1}\) = 3 см
\(v_{1}\) = 10 см/с
\(x_{2}\) = 5 см
\(v_{2}\) = 6 см/с
|
|
A - ?
\(\omega\) - ?
|
Розв’язання
Припустимо, що рівняння руху точки має вигляд
|
|
\(x=A\sin(\omega{t}+\varphi_{0})\), |
(1) |
де \(\varphi_{0}\) – початкова фаза, t – час. Тоді її швидкість
|
|
\(v_{x}=x^{\prime}(t)=A\omega\cos(\omega{t}+\varphi_{0})\). |
(2) |
Виключимо з рівнянь (1) і (2) час t, скориставшись основною тригонометричною тотожністю \(\sin^{2}\alpha+\cos^{2}\alpha=1\):
|
|
\(\left. \begin{align} \sin(\omega{t}+\varphi_{0})=\frac{x}{A} \\ \cos(\omega{t}+\varphi_{0})=\frac{x}{A\omega} \\ \end{align} \right\} \) \(\Rightarrow\) \(\frac{x^{2}}{A^{2}}+\frac{v^{2}}{A^{2}\omega^{2}}=1\). |
(3) |
(Такий прийом дуже часто є продуктивним у задачах на гармонічні коливання, коли немає необхідності у визначенні моменту часу, або він не заданий в умові задачі).
Далі, записавши вирази (3) для обох пар заданих величин ((x1, v1); (x2, v2)) і прирівнявши їхні ліві частини, отримаємо шукану частоту:
$x_{1}^{2}+\frac{v_{1}^{2}}{{{\omega }^{2}}}=x_{2}^{2}+\frac{v_{2}^{2}}{{{\omega }^{2}}}\quad \Rightarrow \quad $\(\omega=\sqrt{\frac{v_{1}^{2}-v_{2}^{2}}{x_{2}^{2}-x_{1}^{2}}}\) = 2 c-1.
Відтак, підставивши це значення в який-небудь вираз (3), знайдемо амплітуду:
А =5,83 см.
Задача 1.3
Визначити
середню шляхову швидкість \(\langle{v}\rangle\) тіла, що здійснює гармонічні коливання, якщо його максимальна швидкість складає \(v_{m}\) = 10 м/с.
|
Дано: \(v_{m}\) = 10 м/с
|
|
\(\langle{v}\rangle\) - ?
|
Розв’язання
Середня шляхова швидкість – це відношення пройденого шляху до часу (див. [І], ф-ла (1.4)):
\(\langle{v}\rangle=\frac{S}{t}\).
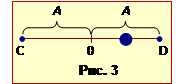
Шлях між крайнми положеннями C і D, рівний подвоєній амплітуді S = 2A коливне тіло проходить за час t = T/2 у пів періоду коливань. Отже, середня шляхова швидкість тіла дорівнює
|
|
\(\langle{v}\rangle=\frac{4A}{T}\). |
(1) |
У той же час максимальна швидкість тіла при гармонічних коливаннях за формулою (1.5б) складає:
\(v_{m}=A\omega=A\frac{2\pi}{T}\).
Тож
\(T=\frac{2\pi{A}}{v_{m}}\),
де \(\omega\) – колова (циклічна) частота.
Підставивши цей вираз у формулу (1), знайдемо відповідь:
\(\langle{v}\rangle=\frac{4Av_{m}}{2\pi{A}}=\frac{2v_{m}}{\pi}\) ≈ 6,4 м/с.
2.2. Динаміка та енергія гармонічних коливань
У розглянутих далі задачах по замовчуванню вважається, що сили тертя та опору відсутні і g = 10 м/с2.
Задача 1.4. Визначити період T малих коливань кульки масою m = 40 г із зарядом $\left| q \right|$ = 8 мкКл, яку підвішено на тонкій шовковій нитці довжиною l = 1 м у напрямленому вертикально вгору електричному полі з напруженістю E = 300 В/см.
Задача 1.5. Пружну кульку на нитці довжиною l = 0,5 м прикріплено до пружної стінки, що нахилена під малим кутом \(\alpha\) до вертикалі, (див. розв'язок, рис. 4). Визначити, з яким інтервалом часу T кулька вдарятиме в стінку, якщо нитку відвести на кут θ0 = 2\(\alpha\) й відпустити.
Задача 1.6. Відкачаний до тиску P = 5 кПа горизонтальний циліндр поперечим перерізом S = 50 см2 поділено рухомим поршнем масою m = 2 кг на дві однакові частини довжиною l = 1 м кожна. Нехтуючи товщиною поршня, визначити період T коливань поршня внаслідок незначного поштовху.
Задача 1.7. Визначити період T та амплітуду A коливань пластини масою M = 1,5 кг на вертикальній пружині жорсткістю k = 250 Н/м після падіння на неї шматка пластиліну масою m = 0,5 кг з висоти h = 20 см.
Задача 1.8. Показати, що потенціальна енергія малих коливань математичного маятника масою m і довжиною l визначається формулою \(W_{п}=\frac{kx^{2}}{2}\), де \(k=\frac{mg}{l}\).
Задача 1.9. Визначити період T гармонічних коливань маятника на момент, коли потенціальна енергія коливань складає n = 80 % від повної, а зміщення з положення рівноваги та швидкість мають значення x = 2 см і v = 3,1 см/с.
Задача 1.4
Визначити
період T малих коливань кульки масою m = 40 г із зарядом $\left| q \right|$ = 8 мкКл, яку підвішено на тонкій шовковій нитці довжиною l = 1 м у напрямленому вертикально вгору електричному полі з напруженістю E = 300 В/см.
|
Дано:
m = 40 г = 0,04 кг
q = 8 мкКл = 8·10–6 Кл l = 1 м E = 300 В/cм = 3·104 В/м
|
| T-? |
Розв'язання
Кулька на нитці являє собою математичний маятник (п. 1.3), тож період її коливань задається загальним виразом (1.13) і формулою (1.18). Але за умовою на кульку, крім сили тяжіння $m\vec{g}$, діє ще й вертикальна електрична сила $q\vec{E}$, як показано на рис. 1.4 для випадку q > 0. Тому у виразі (1.16) замість mg має стояти \(\left| mg\mp \left| q \right|E \right|\). Тож
$k=\frac{\left| mg\mp \left| q \right|E \right|}{l}$,
де знак ''–'' відповідає випадку q > 0 і навпаки.
В такому разі період коливань кульки визначається виразом
|
$T=2\pi \sqrt{\frac{ml}{\left| mg\mp \left| q \right|E \right|}}$ |
Обчислення дають наступні значення:
q > 0 : T = 3,14 с; q < 0 : T = 1,57 с.
Задача 1.5.
Пружну кульку на нитці довжиною l = 0,5 м прикріплено до пружної стінки, що нахилена під малим кутом \(\alpha\) до вертикалі, рис 4.
Визначити,
з яким інтервалом часу T кулька вдарятиме в стінку, якщо нитку відвести на кут θ0 = 2\(\alpha\) й відпустити.
|
Дано: l = 0,5 м
|
|
T - ?
|
Розв’язання
Відповідно до умови кулька стикається зі стінкою пружньо, тобто без утрати енергії, й 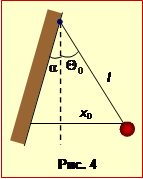 через рівні проміжки часу T, а в проміжках рухається, як математичний маятник за загальним рівнянням (1.4). Отже, якщо початкову координату кульки (відхилення від вертикалі) позначити як x0, то далі вона змінюється за законом
через рівні проміжки часу T, а в проміжках рухається, як математичний маятник за загальним рівнянням (1.4). Отже, якщо початкову координату кульки (відхилення від вертикалі) позначити як x0, то далі вона змінюється за законом
|
$x\left(t\right)={{x}_{0}}\cos {{\omega }}t$. |
(1) |
З урахуванням співвідношення між кутами \(\alpha\) і \(\Theta_{0}\), координата кульки на момент зіткнення зі стінкою t1 дорівнює x1 = –0,5x0, тож із рівняння (1) маємо:
$\cos \omega {{t}_{1}}=-0,5\quad \Rightarrow \quad \omega {{t}_{1}}=\frac{2\pi }{3}$
Відтак, узявши до уваги формулу (1.17) і те, що інтервал часу між послідовними зіткненнями кульки зі стінкою T = 2t1, отримаємо наступну відповідь задачі:
$T=\frac{4\pi }{3}\sqrt{\frac{l}{g}}$ = 0,95 с
Задача 1.6
Відкачаний до тиску P = 5 кПа горизонтальний циліндр перерізом S = 50 см2 поділено рухомим поршнем масою m = 1 кг на дві частини довжиною l = 1 м кожна. Нехтуючи товщиною поршня,
визначити
період T коливань поршня внаслідок незначного поштовху.
Дано:
|
l = 1 м
m = 2 кг
S = 50 см2 = 5·10–3 м2
P = 5 кПа = 5·103 Па
|
|
T - ? |
Розв’язання
При відведенні поршня з рівноважного положення в будь-який бік компенсація сил тиску повітря ${{\vec{F}}_{1}}$, ${{\vec{F}}_{2}}$ (рис. 6 ) порушується так, що їхня рівнодійна $\vec{F}$ є спрямована протилежно й має проєкцію на вісь ОХ
|
Fx = (Р1 – Р2)S. |
(1) |
Тому після вивільнення поршень починає коливатися з періодом, який визначається залежністю Fx(х) повертаючої сили від зміщення x поршня з положення рівноваги. Ця залежнічсть на загал може бути складною, але в даній задачі ситуація спрощується тим, що при малих коливаннях поршня температура повітря в циліндрі лишається сталою. Тож зміна його тиску та об'єму відбувається ізотермічно і є підпорядкована закону Бойля-Маріотта ([ІІІ], п. 1.3) Отже, P1V1 = P2, V2 = PV і, врахувавши, що V1 = (l + x)S, V2 = (l – x)S і V = l S, маємо:
\(Pl=P_{1}(l-x)\) \(\Rightarrow\) \(P_{1}=\frac{Pl}{l-x}\);
\(Pl=P_{2}(l+x)\) \(\Rightarrow\) \(P_{2}=\frac{Pl}{l+x}\).
У такому разі
\(F_{x}=PlS\left(\frac{1}{l+x}-\frac{1}{l-x}\right)=-PlS\frac{2x}{l^{2}-x^{2}}\).
За умовою \(x\ll{l}\), тож величиною \(x^{2}\) у цьому виразі можна знехтувати, тож
|
|
\(F_{x}=-kx\), |
|
де
|
|
\(k=\frac{2PS}{l}\). |
|
Отриманий вираз \(F_{x}\) збігається з формулою (1.10). Отже, малі, коливання поршня є гармонічними, тож шуканий період T, згідно із загальною формулою (1.13), дорівнює
$T=2\pi \sqrt{\frac{ml}{2PS}}$ ≈ 1,3 c.
Задача 1.7
Визначити
період T та амплітуду A коливань пластини масою M = 1,5 кг на вертикальній пружині жорсткістю k = 250 Н/м після падіння на неї шматка пластиліну масою m = 0,5 кг з висоти h = 20 см (рис. 7).
|
Дано: k = 250 Н/м
M = 1,5 кг
h = 20 см = 0,2 м
m = 0,5 кг
|
|
T - ? A - ?
|
Розв’язання
Після падіння пластиліну на пластину створюється пружинний маятник (п. 1.3) масою (M + m) і жорсткістю k. Отже, шуканий період коливань T за формулою (1.15) дорівнює
| \(T=2\pi\sqrt{\frac{m+M}{k}}=\) 0,57 c. | (1) |
Спосіб 1. При зіткненні в точці О з координатою x = 0 пластилін пердає пластині деякий імпульс, через що її наступні коливання відбуваються з відповідною швидкістю v0 й
Коливання пластини з пластиліном відбуваються навколо точки O1, на відстані х0 від початкового положення, що визначається умовою компенсації сумарної ваги тіл і сили, з якою на них діє пружина:
| $ \left( M+m \right)g=k{{x}_{0}} $ $\Rightarrow $ ${{x}_{0}}=\frac{\left( M+m \right)g}{k}$ |
(2) |
При цьому коливання відбуваються не зі стану спокою, як зазвичай, а з певною початковою швидкістю v0, що визначається законом збереження імпульсу. Тож, зважаючи на непружний характер зіткнення
$mv=\left( M+m \right){{v}_{0}}$,
де v – швидкість пластиліну на момент падіння на пластину, котра складає (див. [І], ф-ла (1.19а)), $v=\sqrt{2gh}$ . Отже, початкова швидкість коливань пластини з пластиліном
| ${{v}_{0}}=\frac{m}{M+m}\sqrt{2gh}$. | (3) |
Рис. 7
Відтак при знайдених початкових умовах (x0, v0), із загальних рівняннь гармонічних коливань (1.4) і (1.5) виходить:
| $x=A\sin \left( \omega t+{{\varphi }_{0}} \right)$ $\Rightarrow $ $\frac{x}{A}=\sin \left( \omega t+{{\varphi }_{0}} \right)$ |
| ${{v}_{x}}=A\omega \cos \left( \omega t+{{\varphi }_{0}} \right)$ $\Rightarrow $ $\frac{{{v}_{x}}}{A\omega }=\cos \left( \omega t+{{\varphi }_{0}} \right)$, |
звідки, враховуючи відому тригонометричну тотожність, отримуємо:
\(\frac{x^{2}}{A^{2}}+\frac{v^{2}}{A^{2}\omega^{2}}=1\) \(\Rightarrow\) \(A=\sqrt{x^{2}+\frac{v^{2}}{\omega^{2}}}\).
Ця рівність виконцється при будь-якому положенні коливного тіла, тож поклавши x = x0, отримаємо :
$A=\sqrt{x_{0}^{2}+\frac{v_{0}^{2}}{{{\omega }^{2}}}}$ = $\sqrt{x_{0}^{2}+\frac{{{\left( {{v}_{0}}T \right)}^{2}}}{4{{\pi }^{2}}}}$
Відтак, узявши отримане напочатку (вираз (1)) значення T та обрахувавши за виразами (2) і (3) значення x0 і v0 , дістанемо:
А = 9,2 см.
Спосіб 2. Амплітуду коливань можна знайти, й спираючися не на співвідношеня механіки коливань. А саме.
Стискання пружини відбувається за рахунок енергії пластини з пластиліном . Тому, якщо прийняти потенціальну енрегію тіл у найнижчій точці за 0, то на момент зупинки вся їхня енергія перейде в енергію деформації пружини на величину відстані x від початкового до крайнього положення пластини. Отже,
$\frac{k{{x}^{2}}}{2}$ = $\frac{\left( M+m \right)v_{0}^{2}}{2}+\left( M+m \right)gx$ \(\Rightarrow\) $k{{x}^{2}}-2\left( M+m \right)gx-\left( M+m \right)v_{0}^{2}=0$
Корені цього рівняння складають:
${{x}_{1,2}}=\frac{\left( M+m \right)g}{k}\pm \sqrt{{{\left( \frac{\left( M+m \right)g}{k} \right)}^{2}}+\frac{\left( M+m \right)v_{0}^{2}}{k}}$
або, враховуючи вирази (2) і (3),
${{x}_{1,2}}={{x}_{0}}\pm \sqrt{{{\left( \frac{\left( M+m \right)g}{k} \right)}^{2}}+\frac{\left( M+m \right)2gh}{k}}$.
Зрозуміло, що другі доданки в цьому виразі визначають макимальне відхилення пластини з пластиліном від точки рівноваги сил, тобто шукану амплітуду коливань. Отже,
${A}=\sqrt{{{\left( \frac{\left( M+m \right)g}{k} \right)}^{2}}+\frac{\left( M+m \right)2gh}{k}}$.
Обчислення дають
A = 9,2 см,
що, природньо, збігається із отриманим раніше значенням. Варто також відмітити, що перший доданок під радикалом дорівнює $x_{0}^{2}$. Отже, пластина з пластиліном, незалежно від їхньої маси та жорсткості пружини, повертаючись із найнижчої точки, підніметься вище початкового положення. Це пояснюється тим, що коливання почалися не зі стану спокою, як зазвичай, і з певною початковою кінетичною енергією.
Задача 1.8
Показати,
що потенціальна енергія малих коливань математичного маятника масою m і довжиною l визначається формулою \(W_{п}=\frac{kx^{2}}{2}\), де \(k=\frac{mg}{l}\).
Розв’язання
Потенціальна енергія маятника обумовлена дією на нього сили тяжіння і виражається формулою
|
|
\(W_{п}=mgh\), |
(1) |
де m – маса маятника, h – висота підйому над положенням рівноваги (див. рис.8). З рис.8 видно, що
|
|
\(h=AO-AB=l-l\cos\alpha\) \(\Rightarrow\) \(h=l(1-\cos\alpha)=2l\sin^{2}\frac{\alpha}{2}\). |
(2) |
Оскільки маятник здійснює малі коливання (\(x\ll{l}\)), то \(\alpha\ll{1}\) рад. Тому \(\sin\frac{\alpha}{2}=\frac{\alpha}{2}\), і вираз (2) набуває вигляду:
\(h=2l\left(\frac{\alpha}{2}\right)^{2}=\frac{l\alpha^{2}}{2}\).
Підставивши його у формулу (1) і зробивши заміну \(\alpha=x/l\), отримаємо
\(W_{п}=\frac{mgx^{2}}{2l}=\frac{kx^{2}}{2}\),
де \(k=\frac{mg}{l}\), що і треба було довести.
Ця задача ілюструє універсальність формули (13.19): вона може бути застосовна до будь-яких гармонічних коливань, а не тільки до коливань під дією сили пружності.
Задача 1.9
Визначити
період T гармонічних коливань маятника на момент, коли потенціальна енергія коливань складає n = 80 % від повної, а зміщення з положення рівноваги та швидкість мають значення x = 2 см і v = 3,1 см/с.
|
Дано: n = 80 %
x = 2 см
v = 3,1 см/с
|
|
T - ? |
Розв’язання
Період коливань тіла на пружині визначається формулою:
|
|
\(T=2\pi\sqrt{\frac{m}{k}}\). |
(1) |
Відношення (m/k) знайдемо через повну енергію коливань:
|
|
\(W=\frac{mv^{2}}{2}+\frac{kx^{2}}{2}=W_{п}\left(\frac{mv^{2}}{kx^{2}}+1\right)\), |
(2) |
де (\(mv^{2}/2\)) – кінетична і (\(kx^{2}/2\)) – потенціальна енергія. Відтак із виразу (2) одержимо
\(\frac{m}{k}=\frac{x^{2}}{v^{2}}\left(\frac{W}{W_{п}}-1\right)\).
і після підстановку у формулу (1) дістанемо відповідь:
\(T=2\pi\frac{x}{v}\sqrt{\frac{W}{W_{п}}-1}=2\pi\cdot\frac{2}{3,1}\sqrt{\frac{1}{0,8}-1}\approx\) 2 c.
3. Задачі для самостійної роботи
|
1.10. |
Точка рухається за рівнянням x=5sin( 2πt + π/3 ) см. Визначити її максимальну швидкість і прискорення. [31,4 см/с; 1,97 м/с2] |
|
1.11. |
Точка здійснює коливання з періодом 24 с і нульовою початковою фазою. За який час вона проходить шлях у пів амплітуди? [2 с; 4 с] |
|
1.12. |
Тіло на невагомій струні здійснює коливатися з періодом 3 с, амплітудою 1 м і початковою фазою 60o. Визначити, який шлях воно проходить за 7 с . [17 м] |
|
1.13. |
Визначити шлях, пройдений за 1 с, і модуль вектора середньої швидкості точки, що здійснює гармонічні коливання з амплітудою 2,5 мм і частотою 1 кГц. [10 м; 0]. |
|
1.14. |
Точка здійснює гармонічні коливання з нульовою початковою фазою. Через яку частину періоду її швидкість дорівнюватиме половині максимальної? [1/6] |
|
1.15. |
Визначити рівняння руху x(t) точки, котра з початкового положення x(0) = 25 мм здійснює гармонічні коливання з періодом 2 с, якщо її максимальне прискорення складає 49,3 см/с2. [x = 5sin( πt + π/6)] |
|
1.16. |
Точка здійснює коливання за рівнянням x = Acos(ωt-π/4). Визначити залежність від координати x її швидкості vx та прискорення ах. [${{v}_{x}}=\pm A\omega \sqrt{1-{{\left( x/A \right)}^{2}}}$; ${{a}_{x}}=-{{\omega }^{2}}x$] |
|
1.17. |
Точка здійснює гармонічні коливання, що відбуваються за законом синуса. Визначити амплітуду коливань, якщо в деякий момент часу координата точки складала x1= 5 см, а на момент, коли фаза подвоїлася, стала рівною x2= 8 см.[8,33 см] |
|
1.18. |
Точка здійснює гармонічні коливання з періодом 0,6 c і амплітудою 10 см. Визначити середню швидкість точки за час, протягом якого вона проходить шлях у пів амплітуди 1) з положення рівноваги і 2) з крайнього положення. [1) 1 м/с; 2) 0,5 м/с] |
|
1.19. |
Координата x та швидкість vx точки, що здійснює гармонічні коливання вздовж осі OX з коловою частотою 4 с-1, на деякий момент складають 25 см і 1 м/с. Знайти їхні значення через 2,4 с по тому. [–29 см; –81 см/с ] |
|
1.20. |
Горизонтальний пружинний маятник (див. п.1.3) здійснює гармонічні коливання з амплітудою А і періодом Т0. Визначити, на якій відстані L від його рівноважного положення слід поставити вертикальну пружну стінку, аби період повторення зіткнень із нею маятника складав Т? [L = Acos(π(1 – (T/T0)))] |
|
1.21. |
Підвішений до пружини тягар розтягає її на 10 см. Визначити період його вертикальних коливань вантажу на цій пружині. [0,63 с] |
| 1.22. |
Визначити прискорення вільного падіння за даними досліду, в якому математичний маятник з довжиною нитки 75 см за 20 с зробив 34 повних коливань. [10,2 м/с2] |
| 1.23. |
Яку довжину має мати математичний маятник, аби період його коливань дорівнював 1 с ? Який період коливань має маятник довжиною 1 м ? [25 см; 2 с] |
|
1.24. |
За однаковий час один маятник здійснює 50 коливань, а інший – 40. Визначити довжини маятників, якщо відрізняються на 45 см. [80 см; 1,25 м] |
|
1.25. |
Мідна кулька на пружині коливається з періодом 1 с . Визначити період коливань алюмінієвої кульки такого ж радіусу на тій самій пружині. Густина міді 8,9 г/см3 ; алюмінію 2,7 г/см3. [0,55 с] |
|
1.26. |
До пружини по черзі підвішують два вантажі. Перший з них розтягує пружину на 1 см. На скільки розтягує пружину другий вантаж, якщо періоди його коливань на пружині у рази більший ніж першого? [4 см] |
|
1.27. |
Якщо до підвішеного на пружині тіла маси 3 кг додати тягарець масою 100 г, то пружина додатково розтягнеться на 3 см. Визначити період вертикальних коливань тіла за відсутності тягарця. [1,9 с] |
|
1.28. |
Два тягарці висять на нитках однакової довжини. Перший підіймають до точки кріплення нитки, а другий відхилюють на малий кут від положення рівноваги й одночасно відпускають. Який з тягарців швидше дійде до положення рівноваги? Визначити відношення відповідних проміжків часу (t1/t2). [перший; 0,9] |
|
1.29. |
Пружну кульку підвісили до стелі неподалік стіни на нитці довжиню 1 м. Визначити період малих коливань кульки, якщо на половині довжини нитки в стіну вбито штифт. [1 с] |
|
1.30. |
Яким має бути прискорення ліфта напочатку руху, аби в ньому період малих коливань математичного маятника змінювався не більше ніж ні 10%? [2 м/с2] |
|
1.31. |
Математичний маятник довжиною 1,2 м підвішено у вагоні, що рухається горизонтально по прямій з прискоренням 2,2 м/с2. Визначити рівноважне положення нитки і період коливань маятника. [12,6° до вертикалі; 2 с ] |
|
1.32. |
Пробірка з тягарцем на дні діаметром 6,5 мм і загальною масою 50 г, що занурена в рідину, здійснює вертикальні коливання з періодом 2,5 с. Визначити густину рідини. [1 г/см3] |
|
1.33. |
Визначити глибину уявної шахти на Землі, на дні котрої період коливань математичного маятника був би таким самим, як на поверхні Місяця, враховуючи, що відношення радіусів і середніх густин речовини планет складає 3,7 і 1,67, відповідно. Радіус Землі прийняти 6400 км [5360 км] |
|
1.34. |
На два роли із відстанню між осями 3,2 м, |
|
1.35. |
За який час маленький кубик зісковзне з ребра (т. А) на дно (т. В) сферичної лунки |
| 1.36. |
Вантаж, підвішений на пружині жорсткістю 4 Н/м, здійснює коливання з амплітудою 5 см. Визначити максимальну кінетичну енергію вантажу. [5 мДж] |
| 1.37. |
Зміщення з положення рівноваги точки, що здійснює гармонічні коливання, дорівнює половині амплітуди. Який відсоток повної енергії коливань на цей момент складає потенціальна енергія? [25%] |
| 1.38. | Тіло маси рухається вздовж осі OX згідно із законом $x=0,2\sin (10\pi +(\pi /2))$. За який час кінетична енергія тіла зменшиться від 1,5 Дж до 1,0 Дж? [8,5 мс] |
|
1.39. |
Пружину з підвішеною до неї кулькою маси 80 г розтягають на 5 см і відпускють. Визначити потенціальну енергію пружини через пів періоду коливань, які відтак почалися, що в стані рівноваги кульки видовження пружини складало 3 см. [32,7 мДж] |
|
1.40. |
Куля на пружмні здійснює горизонтальні коливання. Визначити відношення кінетичної енергії кулі до потенціальної енергії пружини на момент, коли ідхилення кулі від рівноважного положення складає пів амплітуди коливань. [3] |
|
1.41. |
Горизонтальний пружинний маятник масою М здійснює коливання з періодом T і амплітудою А. Якими стануть ці характеристики після того, як на маятник у момент проходження положення рівноваги зверху впаде й прилипне шматок пластиліну маси m. \(\left[ {{T}_{1}}=T\sqrt{\frac{M+m}{M}};\ {{A}_{1}}=A\sqrt{\frac{M}{M+m}} \right]\)\ |
|
1.42. |
Знайти, в яких межах змінюється сила натягу нитки математичного маятника масою m і довжиною нитки l при гармонічних коливаннях з амплітудою A. \(\left( 1-{{\left( A/l \right)}^{2}} \right)\le F\le \left( 1+{{\left( A/l \right)}^{2}} \right)\) |
|
1.43. |
Повна енергія коливань кульки масою 40 г на нитці довжиною 1 м дорівнює 50 мДж. Визначити їхню амплітуду [ 48 см] |
|
1.44. |
Як зміниться максимальний кут відхилення математичного маятника, якщо нитку укоротити від 1 м до 80 см і надати йому попередньої максимальної швидкості? [зросте в ≈ 1,1 раза] |
|
1.45. |
Через яку частину періоду після початку коливань математичного маятника його потенціальна енергія зрівняється з кінетичною? [T / 8] |
|
1.46. |
На горизонтальній дошці, що здійснює поздовжні гармонічні коливання, знаходиться брусок. Чому дорівнює коефіцієнт тертя між бруском і дошкою, якщо при періоді її коливань T < 1 с брусок починає ковзати. [0,4] |
|
1.47. |
Прикріплену до пружини жорсткістю 50 Н/м кульку маси 50 г піднімають до положення нерозтягненої пружини й відпускають. Визначити період, амплітуду та максимальну швидкість коливань кульки. [0,2 с; 1 см; 0,3 м/с] |
Розділ ІІ. Електромагнітні коливання. Змінний струм
|
Електромагнітними коливаннями називають процеси в електричних колах, які супроводжуються багаторазовою змінюється сила й напрям струму та величина й полярність напруги на ділянках кола. Існують і знаходять практичне застосування різні типи Електричні коливання можуть мати різний вигляд, але всі вони поділяються на вільні та вимушені. Вільні коливання спостерігаються в коливальних контурах – колах, які містять конденсатори і котушки індуктивності. Вимушені електричні коливання можуть існувати в будь-якому колі й називаються змінним струмом. Вони створюються в будь-якому замкненому колі, що містить джерело змінної ЕРС (генератор). Розділ включає: |
1. Теоретичні відомості
У наступних коротких теоретичних відомостях розглянуто теми:
1.1. Вільні коливання у контурі
|
Вільні електричні коливання спостерігаються у коливальному контурі, причому в ідеальному контурі вони є гармонічними. Повну інформацію про коливання містить диференціальне рівняння коливального контуру. Зокрема, з нього можна визначити частоту і період вільних коливань, одержати рівняння коливань заряду, напруги і сили струму в контурі. У коливальному контурі відбуваються перетворення електричної і магнітної енергії коливань. |
В електричному колі, що складається з конденсатора, котушки індуктивності та резистора, за який зазвчай правлять з'єднувальні провідники, за певних співвідношень між параметрами можуть виникати вільні електричні коливання. Тому таке коло називається коливальним контуром.
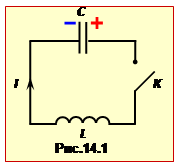 У теорії електичних коливань базовою моделлю є ідеальний коливальний контур, який складається з ідеального конденсатора та ідеальної котушки індуктивності, котрі з'єднані провідниками, що не мають електричного опору (рис.14.1). Отже, в ідеальному контурі при протіканні струму немає втрат енергії, а електричне й магнітне поля повністю зосереджені всередині конденсатора та котушки, відповідно.
У теорії електичних коливань базовою моделлю є ідеальний коливальний контур, який складається з ідеального конденсатора та ідеальної котушки індуктивності, котрі з'єднані провідниками, що не мають електричного опору (рис.14.1). Отже, в ідеальному контурі при протіканні струму немає втрат енергії, а електричне й магнітне поля повністю зосереджені всередині конденсатора та котушки, відповідно.
Електричні коливання в контурі виникають наступним чином. При замиканні ключа K конденсатор починає розряджатися, створюючи в котушці струм та зустрічну ЕРС самоіндукції ([ІІІ], ф-ла (3.15)). Тому струм встановлюється не одразу, а поступово і, досягнувши певної величини, так само поступово спадає. При цьому, через ЕРС самоіндукції, на момент розрядки конденсатора (q = 0, U = 0) струм у контурі не припиняється, тож конденсатор не розряджається, а перезаряджається до вихідної напруги. А далі все повторюється знову й знову, тож у контурі виникають незагасаючі вільні електричні коливання.
Описані процеси математично виражаються диференціальним рівнянням ідеального контуру, котре ґрунтується на тому, що в будь-який момент напруга на конденсаторі u збігається з ЕРС самоіндукції \({{\E}_{c}}\) в котушці:
|
\(u={{\E}_{c}}\). |
Величини u і \({{\E}_{c}}\) визначаються формулами ([ІІІ], (2.23) і (3.14)), отже
|
|
\(\frac{q}{C}=-Li^{\prime}\), |
(2.1) |
де q – заряд конденсатора, \(i^{\prime}\) – похідна сили струму по часу.
Струм у контурі створюється перенесенням заряду з однієї обкладки конденсатора на іншу, тому миттєва сила струму i в контурі дорівнює швидкості зміни заряду конденсатора, котра визначається похідною заряду по часу:
|
|
\(i=q^{\prime}\). |
(2.2) |
Відповідно,
|
|
\(i^{\prime}=q^{\prime\prime}(t)\). |
(2.3) |
і, зробивши таку заміну у виразі (2.1), дістанемо диференціальне рівняння ідеального контуру:
|
|
\(q^{\prime\prime}=-\frac{1}{LC}q\), |
(2.4) |
котре за формою і загальним змістом є ідентичним із рівнянням (1.21). А це означає, що
|
вільні електричні коливання в ідеальному контурі є гармонічними |
і відбуваються з циклічною частотою
|
|
\(\omega=\frac{1}{\sqrt{LC}}\). |
(2.5) |
Відповідно, їхній період визначається формулою Томсона:
|
|
\(T=2\pi\sqrt{LC}\), |
(2.6) |
а лінійна частота
|
|
\(\nu=\frac{1}{2\pi\sqrt{LC}}\). |
(2.7) |
Рівняння коливань заряду конденсатора в ідеальному контурі можна одержати з рівнянь механічних коливань заміною x → q. Зокрема, з рівняння (1.4) дістаємо:
|
|
\(q=q_{m}\cos(\omega{t}+\varphi_{0})\), |
(2.8) |
Напруга на конденсаторі \(u=q/C\) (розділ ІІ, (1.23)), тож рівняння коливань напруги на конденсаторі ідеального контуру має вигляд:
|
|
\(u=U_{m}\cos(\omega{t}+\varphi_{0})\), |
(2.9) |
де Um – амплітуда напруги, що визначається як
|
|
\(U_{m}=\frac{q_{m}}{C}\). |
(2.10) |
Оскільки сила струму в контурі \(i=q^{\prime}(t)\), то сила струму в ідеальному контурі:
|
|
\(i=-\omega{q}_{m}\sin(\omega{t}+\varphi_{0})\) |
(2.11) |
|
|
\(i=I_{m}\cos\left(\omega{t}+\varphi_{0}+\frac{\pi}{2}\right)\), |
(2.11a) |
де амплітуда сили струму
|
|
\(I_{m}=\omega{q}_{m}\). |
(2.12) |
З рівнянь (2.9) і (2.11а) видно, що в ідеальному контурі коливання сили струму випереджають по фазі коливання напруги на конденсаторі на \(\pi/2\) або на чверть періоду (рис.14.2).
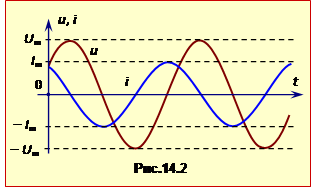
(Коливання заряду на конденсаторі завжди мають таку саму фазу, що й коливання напруги (див. рівняння (2.8) та (2.9)). Тому графік q(t) на рис.14.2 не показан0).
Енергія коливань в ідеальному контурі складається з енергії електричного поля конденсатора WE та енергії магнітного поля котушки індуктивності WB:
|
|
W = WE + WB. |
(2.13) |
Відповідно до формул ([III] (2.32а), (3.16)) і рівнянь (2.9), (2.11а)
|
|
\(W_{Е}=\frac{q_{m}^{2}}{2C}\cos^{2}(\omega{t}+\varphi_{0})\) =\(\frac{q_{m}^{2}}{4C}\left(1+cos(2\omega{t}+2\varphi_{0})\right)\), |
(2.14) |
|
|
\(W_{В}=\frac{LI_{m}^{2}}{2}\sin^{2}(\omega{t}+\varphi_{0})=\frac{LI_{m}^{2}}{2}\left(1-\cos(2\omega{t}+2\varphi_{0})\right)\). |
(2.15) |
З виразів (2.12) та (2.5) виходить:
\(LI_{m}^{2}=L\omega^{2}q_{m}^{2}\) \(\Rightarrow\) \(LI_{m}^{2}=\frac{q_{m}^{2}}{C}\).
Тому з виразів (2.13), (2.14) і (2.15) очевидно, що
|
|
\(W=\frac{q_{m}^{2}}{2C}=\frac{LI_{m}^{2}}{2}\) = const. |
(2.16) |
Таким чином,
|
повна енергія вільних коливань в ідеальному контурі зберігається, тобто не залежить від часу. |
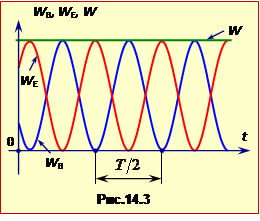 На рис.14.3 показано графіки залежності від часу електричної WE, магнітної WB і повної енергії коливань W в ідеальному контурі.
На рис.14.3 показано графіки залежності від часу електричної WE, магнітної WB і повної енергії коливань W в ідеальному контурі.
Ці графіки наочно показують, що при вільних коливаннях в ідеальному контурі відбуваються неперервні взаємні перетворення електричного та магнітного полів без втрати енергії. Крім того, з рівнянь (2.14) і (2.15) випливає, що коливання енергії кожного з полів відбуваються з подвоєною частотою \(\omega^{\prime}\) відносно коливань напруги і струму:
|
\(\omega^{\prime}=2\omega\) |
або |
\(T^{\prime}=\frac{T}{2}\). |
Порівняння формул (2.16) і (13.21) показує їх математичну ідентичність. При цьому для контуру величини (1/C) і L виконують ту ж саму роль, що й жорсткість пружини k та маса вантажу m у випадку пружинного маятника.
1.2. Змінний струм
|
Змінним струмом називаються вимушені коливання в електричному колі, підключеному до джерела ЕРС якого періодично змінюється з часом. В елементарній фізиці розглядаються тільки синусоїдальні змінні струми. Такі струми повсюдно використовуються в електротехніці та побуті. Але в електроніці широко застосовують й інші змінні струми. У загальному випадку коло змінного струму, крім джерела (генератора) та резисторів, містить конденсатори і котушки індуктивності, котрі теж мають свій опір. Тому в колах змінного струму вирізняють активний і реактивні ємнісний та індуктивний опори. Тож зв'язок між струмом і напругою (ЕРС) генератора визначається повним опором кола і описується законом Ома для змінного струму. За певних умов у колах змінного струму спостерігається резонанс – явище, котре має важливі практичні застосування. Потужність змінного струму залежить не тільки від напруги і сили струму, але й від різниці фаз коливань цих величин. Специфічним для кіл змінного струму є також використання трансформаторів – пристроїв для перетворення напруги та сили струму. |
Серед різноманітних змінних струмів найпростішим є синусоїдальний струм, який створюється генератором із напругою (ЕРС)
|
|
\(u=U_{m}\sin\omega{t}\), |
(2.17) |
або
|
$u={{U}_{m}}\cos \left( \omega t-\frac{\pi }{2} \right)$, |
(2.17а) |
де Um – амплітуда, \(\omega\) – циклічна частота (рад/с).
У техніці змінний струм характеризують лінійною частотою
$\nu =\frac{\omega }{2\pi }$ (Гц)
![]()
Генератор змінного струму на електричних схемах зображують так:
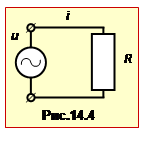 Активним опором R (рис.14.4) називають опір резистора в колі змінного струму. Він, як і при постійному струмі, є зумовлений гальмуванням упорядкованого руху носіїв струму іншими частинками провідника. Тож для змінного струму в резисторах є дійсними всі закони постійного струму, зокрема закон Ома:
Активним опором R (рис.14.4) називають опір резистора в колі змінного струму. Він, як і при постійному струмі, є зумовлений гальмуванням упорядкованого руху носіїв струму іншими частинками провідника. Тож для змінного струму в резисторах є дійсними всі закони постійного струму, зокрема закон Ома:
|
\(i=\frac{u}{R}\), |
(2.18) |
де i та u – миттєві значення сили струму і напруги на резисторі, R – його опір. Отож, якщо на резистор подати напругу, що змінюється за законом (2.17), струм у ньому буде змінюватися так само:
|
|
\(i=I_{m}\sin\omega{t}\), |
(2.19) |
де амплітуда
|
|
\(I_{m}=\frac{U_{m}}{R}\). |
(2.20) |
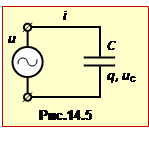 Ємнісним опором називається опір, що створюється в колі змінного струму ідеальним конденсатором.
Ємнісним опором називається опір, що створюється в колі змінного струму ідеальним конденсатором.
Напруга на конденсаторі кожної миті дорівнює напрузі генератора (формула (2.17)), до якого він підключений (рис.14.5). Отже, заряд конденсатора q = Cu змінюється з часом за законом
|
\(q=CU_{m}\sin\omega{t}\). |
(2.21) |
При цьому через з'єднувальні провідники і генератор протікає струм, який називається струмом конденсатора і, позаяк за означенням і = q′ ([ІІІ], ф-ла (2.2)), складає:
|
|
\(i=\omega{C}U_{m}\cos\omega{t}\), |
(2.22) |
або
|
|
\(i=I_{m}\sin\left(\omega{t}+\frac{\pi}{2}\right)\), |
(2.22a) |
де ${{I}_{m}}=\omega C{{U}_{m}}$ – амплітуда струму.
(Зауважимо, що струм конденсатора – абстрактне поняття, адже він зумовлюється не рухом зарядів між обкладками конденсатора, а зміною напруги на ньому.)
По аналогії з виразом (2.20) амплітуду струму конденсатора можна записати, як
|
\(I_{m}=\frac{U_{m}}{(1/\omega{C})}\). |
(2.23) |
Отже, струм конденсатора при заданій напрузі обмежується величиною
|
|
\(X_{C}=\frac{1}{\omega{C}}=\frac{1}{2\pi\nu{C}}\), |
(2.24) |
яка називається ємнісним опором.
Таким чином, для змінного струму в конденсаторі зв'язок між амплітудами струму Im і напруги Um є аналогічний такому для постійного струму:
|
|
${{I}_{m}}=\frac{{{U}_{m}}}{{{X}_{c}}}$, |
(2.24) |
Але, як видно з рівнянь (2.22) і (2.17), для миттєвих значень
$i\ne \frac{u}{{{X}_{c}}}$,
тобто,
| для миттєвих значень струму і напруги на конденсаторі закон Ома не виконується. |
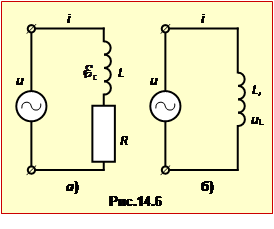 У колі змінного струму котушка теж створює специфічний індутривний опір, за який є відповідальним явище самоіндукції ([ІІІ], п. 1.4) Якщо котушку з індуктивністю L і активним опором R підключити до генератора змінної напруги (рис.14.6а), то струм i в ній буде визначатися не тільки напругою генератора \(u=U_{m}\sin\omega{t}\), а й ЕРС самоіндукції ${{\E}_{c}}=-L{i}'$, так що
У колі змінного струму котушка теж створює специфічний індутривний опір, за який є відповідальним явище самоіндукції ([ІІІ], п. 1.4) Якщо котушку з індуктивністю L і активним опором R підключити до генератора змінної напруги (рис.14.6а), то струм i в ній буде визначатися не тільки напругою генератора \(u=U_{m}\sin\omega{t}\), а й ЕРС самоіндукції ${{\E}_{c}}=-L{i}'$, так що
$iR={{U}_{m}}\sin \omega t-L{i}'$
Звідси для струму в ідеальній (R = 0) котушці (рис.14.6б) отримуємо наступне диференціальне рівняння
|
${i}'=\frac{{{U}_{m}}}{R}\sin \omega t$, |
(2.25) |
з якого випливає, що струм змінюється за законом
|
|
\(i=I_{m}\sin\left(\omega{t}-\frac{\pi}{2}\right)\), |
(2.26) |
де величина
|
\(I_{m}=\frac{U_{m}}{X_{L}}\) |
(2.27) |
є його амплітудою, а
|
|
\(X_{L}=\omega{L}=2\pi\nu{L}\) |
(2.28) |
— індуктивним опором котушки.
Отже, для котушки індуктивності зв'язок між амплітуди струму Im і напруги Um в котушці індуктивності є пов'язані між собою так, як і резисторі та конденсаторі. Але для миттєвих значень такого зв'язку немає:
\(i\ne{u}/X_{L}\).
Отже, як і в конденсаторі,
|
миттєві значення сили змінного струму і напруги в котушці індуктивності закон Ома не задовольняють. |
Зрозуміло, що розглянутий зв'язок між амплітудами є чинним і в нерозгалуженому (послідовному) колі, що містить всі три види опордв. Це відображає закон Ома для змінного струму:
|
амплітуда сили змінного струму в колі є прямо пропорційна амплітуді напруги (ЕРС) генератора і обернено пропорційна повному опору кола: |
|
|
\(I_{m}=\frac{U_{m}}{Z}\). |
(2.29) |
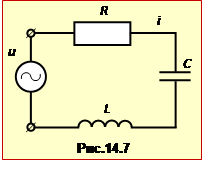 При цьому повний опір Z, інакше — "імпеданс", визначається параметрами елементів кола (R, L, C) і способом їхнього з'єднання. Для найпростішого послідовного кола (рис.14.7)
При цьому повний опір Z, інакше — "імпеданс", визначається параметрами елементів кола (R, L, C) і способом їхнього з'єднання. Для найпростішого послідовного кола (рис.14.7)
|
\(Z=\sqrt{R^{2}+(X_{L}-X_{C})^{2}}\), |
(2.30) |
або
|
\(Z=\sqrt{R^{2}+\left(\omega{L}-\frac{1}{\omega{C}}\right)^{2}}\). |
(2.31) |
Закон Ома для змінного струму стосується тільки амплітуд. Для миттєвих значень сили струму він не виконується, тобто сила струму в даний момент часу не дорівнює відношенню напруги в цей момент до повного опору. Але це не суперечить співвідношенню (2.29), тому що сила струму і напруга здійснюють коливання зі зсувом фаз і досягають своїх максимальних значень Im і Um не одночасно.
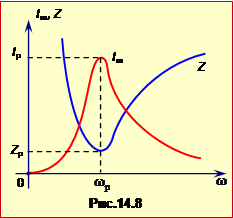 Згідно з виразом (2.31), Повний опір Z , тож і амплітуда сили струму, залежать від частоти, як показує рис.14.8. Він, зокрема, відображує явище резонансу в колі змунного струму, що полягає у різкому збільшенні амплітуди при наближенні коливань струму до резонансної частоти \(\omega_{р}\), яка відповідає мінімуму повного опору кола й знаходиться з умови
Згідно з виразом (2.31), Повний опір Z , тож і амплітуда сили струму, залежать від частоти, як показує рис.14.8. Він, зокрема, відображує явище резонансу в колі змунного струму, що полягає у різкому збільшенні амплітуди при наближенні коливань струму до резонансної частоти \(\omega_{р}\), яка відповідає мінімуму повного опору кола й знаходиться з умови
|
\(\omega_{р}L-\frac{1}{\omega_{р}C}\) = 0 \(\Rightarrow\) \(\omega_{р}=\frac{1}{\sqrt{LC}}\), |
(2.32) |
що збігається із власною частотою ідеального контутру з такими самою ємністю та індуктивністю (фомула 2.16).
При резонансі повний опір Zр і резонансна амплітуда струму Iр відповідно до формул (2.31) та (2.29), дорівнюють
\(Z_{0}=R\),
\(I_{р}=\frac{U_{m}}{R}\).
Видно, що при резонансі відбувається компенсація ємнісного й індуктивного опорів. Це пояснюється тим, що напруга на конденсаторі й котушці змінюються в протифазі, тож віднімаються.
Потужність змінного струму, що виділяється в колі у кожний момент часу, дорівнює добутку миттєвих значень сили струму і напруги. Ця миттєва потужність змінюється з великою частотою і її достатньо складно безпосередньо виміряти. Тому на практиці потужністю змінного струму називають середнє значення добутку сили струму й напруги.
Повна потужність у колі змінного струму виражається формулою
|
|
\(P=\frac{1}{2}I_{m}U_{m}\cos\varphi\), |
(2.33) |
де Im, Um – амплітуди сили струму і напруги генератора, \(\varphi\) – різниця фаз між коливаннями струму і напруги генератора.
Величина \(\cos\varphi\) називається коефіцієнтом потужності і виражається через активний і повний опір кола формулою
|
|
\(\cos\varphi=\frac{R}{Z}\). |
(2.34) |
Якщо підставити цей вираз у формулу (2.33) і врахувати закон Ома (формула (2.29), то виходить
|
|
\(P=\frac{I_{m}^{2}}{2}R=\frac{U_{Rm}^{2}}{2R}\), |
(2.35) |
де U = ImR – напруги на активному опорі кола.
Така ж потужність виділялася б у колі постійного струму з опором R при силі струму і напрузі
|
|
\(I=\frac{I_{m}}{\sqrt{2}}\), \(U=\frac{U_{m}}{\sqrt{2}}\). |
(2.36) |
Величини I та U, що визначаються формулами (2.36), називаються діючими, або ж ефективними значеннями сили струму і напруги.
Діючі значення є загальноприйнятими практичними характеристиками змінного струму. Зокрема, електровимірювальні прилади показують діючі значення, тож номінальні величини струмів і напруг на побутових приладах теж вказують у діючих значеннях.
Зважаючи на зв'язок між діючими значеннями та амплітудами, для діючих значень теж виконується закон Ома:
|
\(I=\frac{U}{Z}\). |
(2.37) |
застосуванням діючих значень струму й напруги формули потужності (2.33) і (2.35) записуються у вигляді
|
|
\(P=IU\cos\varphi\), |
(2.38) |
та
|
|
\(P=I^{2}R=\frac{U^{2}}{R}\). |
(2.39) |
Остання формула показує, що споживана від генератора потужність змінного струму, виділяється тільки на активному опорі, а реактивні елементи – конденсатор і котушка індуктивності – енергії не споживають. Це пов'язано з тим, що при зарядці конденсатор поглинає відповідну енергію, а при розрядці – повністю повертає її в коло. Те ж саме відбувається і у котушці індуктивності при збільшенні і зменшенні сили струму.
Одним із специфічних елементів кола змінного струму є трансформатор – пристрій для зміни ("трансформації") напруги від її значення на вході до потрібної величини на виході.
Найпростіший трансформатор складається з двох обмоток (намотаних ізольованим дротом котушок), які надіто на замкнене залізне осердя (рис. 14.9 ). Обмотка, на котру подається вхідна напруга, называється первинною, а інша – вторинною. Якщо напруга на вторинній обмотці ${{U}_{2}}$ більша, ніж на первинній ${{U}_{1}}$, трансформатор називають підвищувальним, інакше (при ${{U}_{2}}<{{U}_{1}}$) – знижувальним.
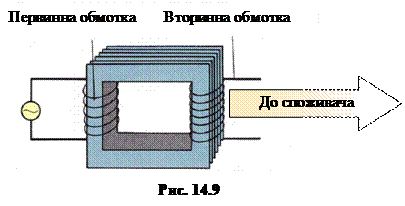
Роботу транcформатора, котра ґрунтується на явищі електромагнітної індукції ([3], п. 1.4), спрощено можна пояснити так. Унаслідок намагнічування осердя струмом первинної обмотки, через поперечний переріз обох обмоток створюється однаковий змінний магнітний потік і, згідно із законом Фарадея ([3], ф-ли (3.11), (3.13)), виникає однакова ЕРС індукції $\varepsilon$ в кожному витку. Тож при кількості витків ${{N}_{1}} і {{N}_{2}}$ у всій обмотці ЕРС індукції ${{\E}_{1}}={{N}_{1}}\varepsilon $ та ${{\E}_{2}}={{N}_{2}}\varepsilon $, відповідно. При цьому величина ${{\E}_{1}}$ задається вхідною напругою
|
${{\E}_{1}}={{U}_{1}}={{N}_{1}}\varepsilon $. |
|
Вторинна обмотка для навантаження (підключених пристроїв) відіграє роль джерела живлення. Тому в режимі "холостого ходу" (коли вторинну обмотку розімкнено) величина ${{\E}_{2}}$ збігається з напругою на клемах:
|
${{\E}_{2}}={{U}_{2}}={{N}_{2}}\varepsilon $ |
|
Таким чином, відношення вхідної та вихідної напруг, яке називається коефіцієнтом трансформації, дорівнює
|
|
$k=\frac{{{U}_{1}}}{{{U}_{2}}}=\frac{{{\E}_{1}}}{{{\E}_{2}}}=\frac{{{N}_{1}}}{{{N}_{2}}}.$ |
(2.40). |
Як видно, для знижувального трансформатора $k>1$, а для підвищувального $k<1$. Отже, величина k формально визначає не лише ступінь, а й напрям зміни напруги на виході трансформатора. Але на практиці вид трансформації визначають словесно. Приміром, говорять "підвищувальний трансформатор з коефіцієнтом трансформації 10", а не 0,1.
Наостанок зауважимо, що наведені викладки, строго говорячи, є наближеними, бо не враховують нявність у обмоток активного опору й витрати енергії струму на їхнє нагрівання та на перемагнічуваня осердя. Але, через порівняно малий активний опір обмоток та специфіку виготовленя осердь, ці втрати є неістотними, і ККД транформаторів є близький до одиниці.
_
Додаток. Розв'язок рівняння (2.25) можна отримати або прямим інтегруванням, або опосередковано, наступним чином. З математики відомо, що (coskx)′ = – k(sinkx), отже
$\sin \omega t=-\frac{1}{\omega }{{\left( \cos \omega t \right)}^{\prime }}$.
Підставивши цей вираз у рівняння (2.26), дістанемо
$L{i}'=\frac{{{U}_{m}}}{\omega }{{\left( \cos \omega t \right)}^{\prime }}$,
звідки випливає вираз
$i=\frac{{{U}_{m}}}{\omega L}\cos \omega t$,
що є рівнозначно виразу (2.26).
2. Приклади розв'язування задач
Розв'язуючи задачі на коливання в ідеальному коливальному контурі і на змінний електричний струм, слід пригадати порядок організації та оформлення розв'язку задач (див. "Етапи розв'язування задач").
У прикладах цього розділу розглянут0:
2.1. Вільні коливання у контурі
2.2. Змінний струм
2.1. Вільні коливання у контурі
Задача 2.1. Ідеальний коливальний контур із повітряним конденсатором і власною частотою ν1 = 41,405 кГц розмістили під вакуумним ковпаком і відкачали повітря, через що власна частота контуру змінилася на Δν = 13 Гц. За цими даними визначити діелектричну проникність повітря ε.
Задача 2.2. В ідеальному контурі ємністю C = 1 мкФ й індуктивністю L = 100 мкГн відбуваються вільні коливання з амплітудою заряду конденсатора qm = 0,1 мкКл. Визначити силу струму i в контурі на момент, коли заряд конденсатора є в k = 3 рази менший за qm.
Задача 2.3. У певний момент часу у вільному коливальному контурі з ємністю C = 20 мкФ й індуктивністю L = 2 мГн напруга на конденсаторі складає u = 10 В, а сила струму в котушці i1 = 2А. Визначити силу струму i в контурі на момент, коли заряд конденсатора є в k = 3 рази менший за qm.
Задача 2.1.
Ідеальний коливальний контур із повітряним конденсатором і власною частотою ν1 = 41,405 кГц розмістили під вакуумним ковпаком і відкачали повітря, через що власна частота контуру змінилася на Δν = 13 Гц. За цими даними
визначити
діелектричну проникність повітря ε.
|
Дано: ν1 = 41,405 кГц Δν = 13 Гц |
|
ε - ? |
Розв’язання
При відкачуванні з конденсатора контуру видаляється діелектрик (повітря). Через це напруженість поля та напруга на обкладках конденсатора зростають, а ємність зменшується, в ε разів. Отож, відношення початкової C1 та кінцевої C2 ємностей дорівнює
$\frac{{{C}_{1}}}{{{C}_{2}}}=\varepsilon $
А відповідно до формули (2.7) воно складає
$\frac{{{C}_{1}}}{{{C}_{2}}}={{\left( \frac{{{\nu }_{2}}}{{{\nu }_{1}}} \right)}^{2}}$
Отже, шукана проникність
$\varepsilon ={{\left( \frac{{{\nu }_{2}}}{{{\nu }_{1}}} \right)}^{2}}$
Відтак, урахувавши, що за умовою ${{\nu }_{2}}={{\nu }_{1}}+\Delta \nu $, отримуємо відповідь:
$\varepsilon ={{\left( 1+\frac{\Delta \nu }{\nu } \right)}^{2}}$.
Обчислення дає
$\varepsilon $ = 1,00063.
Примітка. Зважаючи на отриману відповідь, умова задачі може здатися не реалістичною, позаяк задана зміна влаcної частоти контуру (Δν/ν) складає всього ≈ 0,02%. Але існуюючі прилади дозволяють вимірювати резонансну частоту контурів із указаною, так що в умові описано реальний лабораторний метод визначення діелектричної проникності газів..
Задача 2.2.
В ідеальному контурі ємністю C = 1 мкФ й індуктивністю L = 100 мкГн відбуваються вільні коливання з амплітудою заряду конденсатора qm = 0,1 мкКл.
Визначити
силу струму i в контурі на момент, коли заряд конденсатора є в k = 3 рази менший за qm.
|
Дано: C = 10–6 Ф
L = 10–4 Гн
\(q_{m}\) = 10–7 Кл
k = 3
|
|
i - ?
|
Розв’язання
Задачу можна розв’язати двома способами.
I спосіб. Нехай заряд конденсатора змінюється з часом за законом (2.8):
|
|
\(q=q_{m}\cos(\omega{t}+\varphi_{0})\), |
(1) |
де \(\omega\) – власна частота контуру й \(\varphi_{0}\) – початкова фаза коливань заряду. Тоді за рівнянням (2.11) сила струму в контурі змінюється як
|
|
\(i=-q_{m}\omega\sin(\omega{t}+\varphi_{0})\). |
(2) |
\(\sin(\omega{t}+\varphi_{0})=-\frac{i}{q_{m}\omega}\), \(\cos(\omega{t}+\varphi_{0})=\frac{q}{q_{m}}\)
і
${{\left( \frac{i}{{{q}_{m}}\omega } \right)}^{2}}+{{\left( \frac{q}{{{q}_{m}}} \right)}^{2}}=1\quad \Rightarrow \quad i={{q}_{m}}\omega \sqrt{1-{{\left( \frac{q}{{{q}_{m}}} \right)}^{2}}}$
Відтак, урахувавши, що \(\frac{q}{q_{m}}=\frac{1}{k}\) і \(\omega=\frac{1}{\sqrt{LC}}\), знайдемо наступну відповідь:
\(i=\frac{q_{m}}{k}\sqrt{\frac{k^{2}-1}{LC}}\) = 94 мА.
II спосіб ґрунтується на законі збереження енергії. А саме.
Через відсутність утрат енергії при вільних коливаннях в ідеальному контурі сумарна енергія електричного WE, і магнітного WB полів лишається сталою:
W = WE + WB = const.
Тому при зміні енергії якогось із полів в один бік енергія іншого змінюється на таку саму величину в протилежний. Через це в будь-який момент часу величина W дорівнює максимальній енергії кожного з полів, яка визначається формулами ([ІІІ], (1.16), або (1.32а)). Отже, можна записати:
\(\frac{q^{2}}{2C}+\frac{Li^{2}}{2}=\frac{q_{m}^{2}}{2C}\) \(\Rightarrow\) \(i=\sqrt{\frac{q_{m}^{2}-q^{2}}{LC}}\),
де за умовою q = (qm/k). Отже маємо таку відповідь:\(i=\frac{q_{m}}{k}\sqrt{\frac{k^{2}-1}{LC}}\) = 94 mA.Зазначимо, що використовування закону збереження енергії, як зазвичай, істотно скоротило розв’язання.Задача 2.3.
У певний момент часу у вільному коливальному контурі з ємністю C = 20 мкФ й індуктивністю L = 2 мГн напруга на конденсаторі складає u = 10 В, а сила струму в котушці i1 = 2А.
Визначити
заряд конденсатора q на момент, коли сила струм у котушці i2 = 1 A.
|
Дано: C = 20 мкФ = 2·10-5 Ф
L = 2 мГн = 2·10-3 Гн
u = 10 В
\(i_{1}\) = 2 А
\(i_{2}\) = 1 А
|
|
q - ?
|
Розв’язання
Для розв’язання задачі скористаємося законом збереження енергії, за яким у будь-який момент часу сумарна енергія електричного та магнітного полів у ідеальному контурі лишається незмінною. Тому для будь-яких двох моментів часу t1 і t2 можна записати
|
WE(t1) + WB(t1) = WE(t2) + WB(t2) |
(1) |
і, врахоауючи вирази ([ІІІ], (1.32б) і (3.16)),
\(\frac{Cu^{2}}{2}+\frac{Li_{1}^{2}}{2}=\frac{q^{2}}{2C}+\frac{Li_{2}^{2}}{2}\) \(\Rightarrow\) \(q=\sqrt{C^{2}u^{2}+LC(Li_{1}^{2}-Li_{2}^{2})}\).
Обчислення дають:
q = 400 мкКл.
Примітка. Як і в попередній задачі, відповідь можна було би отримати через рівняння коливань в конденсаторі. Але це було би набагато важче.
2.2. Змінний струм
У наведених задачах розглядаються тільки синусоїдальні напруги та струми, і в умовах, якщо не вказано інше, фігурують діючі (''ефективні'') значення цих величин. Окрім того, конденсатори й котушки індуктивності по замовчуванню вважаються ідеальними.
Задача 2.4. При подачі на газорозрядну лампу змінної напруги вона загоряється й гасне, коли напруга на електродах сягає заданої величини Uз (''напруги загоряння''). Знайти, який відсоток часу ввімкнення \(\eta\) горить лампа при напрузі U = Uз.
Задача 2.5. У мережу змінного струму ввімкнено ланцюжок із послідовно з'єднаних резистора R = 100 Ом і двох запаралелених конденсаторів по C = 30 мкФ. Визначити відношення сил струму в ланцюжку до (I1) та після (I2) пробою одного з конденсаторів.
Задача 2.6. Сила струму в котушці з індуктивністю L = 30 мГн при підключенні до батареї з малим внутрішнім опором і ЕРС \({\E}\) = 9 В складає I1 = 1 A. Якою вона буде, якщо на котушку подати змінну напругу \(U={\E}\) промислової частоти $\nu $ = 50 Гц?
Задача 2.7. Послідовно з'єднані конденсатор змінної ємності С, котушку індуктивності L = 340 мГн і резистор R = 2 Ом увімкнено в мережу з напругою U = 220 В і частотою [\{\nu}=50\)Гц. Визначити: А) величину C, при якій струм у колі буде максимальним; Б) напругу UC, UL і UR на кожній ділянці за такої умови.
Задача 2.8. Послідовний ланцюг із котушки індуктивності L = 6 мкГн, конденсатора С = 0,01 мкФ і резистора R = 0,5 Ом підключено до генератора з регульованою частотою. Визначити потужність P, що виділяється в ланцюзі при резонансній частоті й амплітуді напруги на конденсаторі ${{U}_{mc}}$= 10В.
Задача 2.9. Обмотки трансформатора, що підвищує напругу від U1 = 100 В до U2 = 3300 В, намотано на кільцевому осерді. Визначити кількості витків N1 і N2 в обмотках, якщо при підключенні до вольтметра пропущеної крізь осердя дротини він показує U = 0,5В.
Задача 2.4
При подачі на газорозрядну лампу змінної напруги вона загоряється й гасне, коли напруга на електродах сягає заданої величини Uз (''напруги загоряння'').
Знайти
який відсоток часу ввімкнення \(\eta\) горить лампа при напрузі U = Uз.
|
Дано: \(U=U_{з}\)
|
|
\(\eta\) - ?
|
Розв’язання
За означенням (2.36) та умовою задачі, напруга загоряння лампи складає
| \(U_{з}\) = \(\frac{U_{m}}{\sqrt{2}}\), |
(1) |
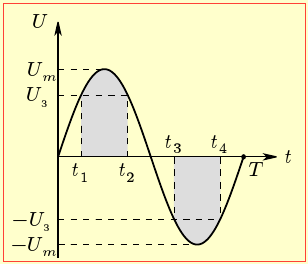
де \(U_{m}\) – амплітуда подаваної напруги. При цьому поточне значення напруги на лампі u(t) визначається рівнянням (2.17):
| u(t) = \(U_{m}\sin\omega{t}\) |
(2) |
Отже, як видно з рис. 8, лампа в кожен період T горить на протязі інтервалу часу
| \(\tau=T-4t_{1}\) |
(1) |
де t1 — проміжок часу, за який напруга на лампі змінюється від 0 до \(U_{з}\) і навпаки. Отже, згідно з виразами (1) і (2),
\(\sin\omega{t}_{1}=\frac{1}{\sqrt{2}}\) \(\Rightarrow\) \(\omega{t}_{1}=\frac{\pi}{4}\).
Звідси, врахувавши зв'язок між частотою та періодом (1.3), знайдемо величину t1:
\(\frac{2\pi}{T}t_{1}=\frac{\pi}{4}\) \(\Rightarrow\) \(t_{1}=\frac{T}{8}\),
та відповідь
\(\tau=T-4\frac{T}{8}=\frac{T}{2}\) \(\Rightarrow\) \(\eta=\frac{\tau}{T}=0,5=50\) %.
Отже, лампа горітиме половину часу перебування під напругою.
Задача 2.5
У мережу змінного струму ввімкнено ланцюжок із послідовно з'єднаних резистора R = 100 Ом і двох конденсаторів по C = 30 мкФ (рис. 9а).
Визначити
відношення сил струму в ланцюжку до (I1) та після (I2) пробою одного з конденсаторів.
|
Дано: \(\nu\) = 50 Гц
R = 100 Ом
C = 30 мкФ = 3·10-5 Ф
|
|
\((I_{1}/I_{2})\) - ?
|
Розв’язання
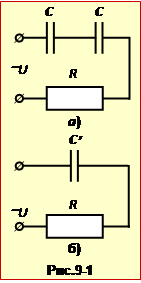 При електричному пробої діелектрика в конденсаторі утворюється провідний канал, який ''закорочує'' (сполучає між собою) його пластини. Тож, замість первісного (рис. 9а), утворюється новий ланцюг (рис. 9б) із тією самою поданою напругою. Тому за законом Ома (2.29)
При електричному пробої діелектрика в конденсаторі утворюється провідний канал, який ''закорочує'' (сполучає між собою) його пластини. Тож, замість первісного (рис. 9а), утворюється новий ланцюг (рис. 9б) із тією самою поданою напругою. Тому за законом Ома (2.29)
${{I}_{1}}{{Z}_{1}}={{I}_{2}}{{Z}_{2}}\quad \Rightarrow \quad $\(\frac{I_{1}}{I_{2}}=\frac{Z_{2}}{Z_{1}}\), (1)
де Z – імпеданс (повний опір) ланцюжка (2.30), який за відсутності котушки індуктивності дорівнбє:
$Z=\sqrt{{{R}^{2}}+X_{c}^{2}}$
При цьому в першому випадку ємність ланцюга за формулою ([3], (1.28а)), дорівнює С1 = (C/2), а в другому С2 = С. Отож, відповідно до виразу (2.23), маємо:
\(Z_{1}=\sqrt{R^{2}+\left(\frac{1}{2\pi\nu(C/2)}\right)^{2}}\) = 234,6 Ом.
\(Z_{2}=\sqrt{R^{2}+\left(\frac{1}{2\pi\nu{C}}\right)^{2}}\) =145,8 Ом.
Відтак із співвідношеня (1), отримуємо відповідь:
\(\frac{I_{1}}{I_{2}}\)\(\approx{0,62}\),
тобто сила струму після пробою збільшиться в \(\approx{1,6}\) раза.
Задача 2.6
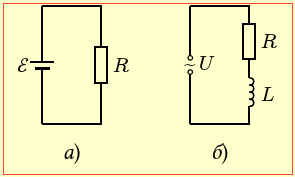
Сила струму в котушці з індуктивністю L = 30 мГн при підключенні до батареї з малим внутрішнім опором і ЕРС \({\E}\) = 9 В складає I1 = 1 A.
Якою вона буде,
якщо на котушку подати змінну напругу \(U={\E}\) промислової частоти $\nu $ = 50 Гц?
|
Дано: L = 0,03 Гн
\({\E}\) = 9 В
\(I_{1}\) = 1 A
$\nu $ = 50 Гц
|
|
I2 - ?
|
Розв’язання
В першому випадку в котушці тече постійний струм, величина якого залежить тільки від активного опору R (опору дроту, яким намотано котушку) і ЕРС джерела. Еквівалентну схему кола для цього випадку показано на рис.10а. Якщо ж струм є змінним, то повний опір кола визначається не тільки опором дроту R, а й індуктивністним опором котушки XL (рис.10б). Отже, відповідно до закону Ома для постійного ([3], (2.10)) та змінного (2.30) струму маємо:
|
|
\(I_{1}=\frac{{\E}}{R}\), \(I_{2}=\frac{U}{Z}\). |
(1) |
Звідси, з урахуванням умови \(U={\E}\), одержуємо:
|
|
\(\frac{I_{2}}{I_{1}}=\frac{R}{Z}\) \(\Rightarrow\) \(I_{2}=I_{1}\frac{R}{Z}\), |
(2) |
де Z – імпенданс (повний опір) котушки. Оскільки в колі немає конденсатора, то опір ємності XC = 0, і з формул (2.31) і (2.28) випливає, що
\(Z=\sqrt{R^{2}+(2\pi\nu{L})^{2}}\).
Підставивши цей вираз у формулу (2), дістанемо:
|
|
\(I_{2}=I_{1}\frac{R}{\sqrt{R^{2}+(2\pi\nu{L})^{2}}}\) = \(I_{1}\frac{1}{\sqrt{1+\left(2\pi\nu{L}/{R}\right)^{2}}}\). |
(3) |
Із формули (1) \(R={\E}/I_{1}\), отже, остаточна відповідь має вигляд:
\(I_{2}=\frac{1}{\sqrt{1/I_{1}^{2}+\left(2\pi\nu{L}/{\E}\right)^{2}}}\).
Обчисленнядають
I2 = 0,7 A.
Задача 2.7
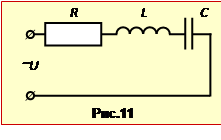 Послідовно з'єднані конденсатор змінної ємності С, котушку індуктивності L = 340 мГн і резистор R = 2 Ом увімкнено в мережу з напругою U = 220 В і частотою \(\nu=50\) Гц.
Послідовно з'єднані конденсатор змінної ємності С, котушку індуктивності L = 340 мГн і резистор R = 2 Ом увімкнено в мережу з напругою U = 220 В і частотою \(\nu=50\) Гц.
Визначити:
А) величину C, при якій струм у колі буде максимальним; Б) напругу UC, UL і UR на кожній ділянці за такої умови.
|
Дано: L = 340 Гн
R = 2 Ом
\(\nu=50\) Гц
|
|
C - ?
UC, UL , UR - ?
|
Розв’язання
А) Згідно з вирзами (2.29) і (2.31), струм у колі буде найбільшим за умовиови Х = 0, тобто
\(\omega{L}-\frac{1}{\omega{C}}=0\) \(\Rightarrow\) \(\omega{L}=\frac{1}{\omega{C}}\).
Звідси знаходимо:
$C=\frac{1}{{{\omega }^{2}}L}=\frac{1}{{{(2\pi \nu )}^{2}}L}$ = 30 мкФ.
Б) За законом Ома (2.37) при Z = R маємо:
\(I_{m}=\frac{U}{R}\).
Підставивши цей вираз у формули (2.25) і (2.28), знаходимо:
\(U_{C}=\frac{I}{\omega{C}}=\frac{U}{2\pi\nu{CR}}=1061\) В;
\(U_{L}=I\omega{L}=\frac{U}{R}2\pi\nu{L}=1061\) В.
В отриманих результатах впадає в очі здавалося б парадоксальний факт – напруги на конденсаторі і котушці майже в 5 разів перевищують напругу джерела, а напруга на резисторі дорівнює напрузі джерела так, ніби конденсатора і котушки у колі немає. Це пояснюється тим, що напруги на конденсаторі й котушці, що завжди є протилежними за фазою, при резоненсі мають однакову величину.
Задача 2.8
Послідовний ланцюг із котушки індуктивності L = 6 мкГн, конденсатора С = 0,01 мкФ і резистора R = 0,5 Ом підключено до генератора з регульованою частотою (рис. 12).
Визначити
потужність P, що виділяється в ланцюзі при резонансній часоті й амплітуді напруги на конденсаторі UрС = 10 В.
Примітка. Для змінного струму слово "потужність" без спеціальних указівок означає середню потужність за період.
|
Дано: L = 6 мкГн = 6·10-6 Гн
С = 0,01 мкФ = 10-8 Ф
R = 0,5 Ом
${{U}_{mc}}$= 10 В
|
|
P - ?
|
Розв’язання
В колі змінного струму енергію споживає тільки на активному опорі. Тому шукана потужність визначається через резонансну амплітуду сили струму ${{I}_{m}}$ та заданий опір резистора формулою (2.35):
|
\(P=\frac{1}{2}I_{m}^{2}R\), |
(1) |
Позаяк усі елементи ланцюга є з'єднані послідовно, потрібну величину ${{I}_{m}}$ знаходимо за 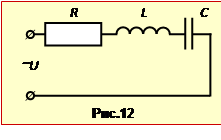 законом Ома (2.25) через задану амплітуду напруги та опір конденсатора (2.23) при резонансній частоті (2.32):
законом Ома (2.25) через задану амплітуду напруги та опір конденсатора (2.23) при резонансній частоті (2.32):
${{I}_{m}}=\frac{{{U}_{m}}C}{\sqrt{LC}}\quad \Rightarrow \quad {{I}_{m}}={{U}_{mc}}\sqrt{\frac{C}{L}}$.
Підставивши цей вираз у формулу (1), отримаємо відповідь:
$P=\frac{U_{mc}^{2}RC}{2L}\approx$41,7 мВт.
Задача 2.9
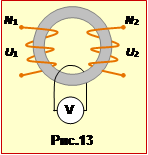 Обмотки трансформатора, що підвищує напругу від U1 = 100 В до U2 = 3300 В, намотано на кільцевому осерді (рис.13).
Обмотки трансформатора, що підвищує напругу від U1 = 100 В до U2 = 3300 В, намотано на кільцевому осерді (рис.13).
Визначити
кількості N1 і N2 витків у обмотках, якщо при підключенні до вольтметра пропущеної крізь осердя дротини він показує U = 0,5 В.
|
Дано: \(U_{1}\) = 100 В
\(U_{2}\) = 3300 В
\(U\) = 0,5 В
|
|
N1, N2 - ?
|
Розв’язання
Дріт разом з вольтметром утворюють замкнутий контур. Його поверхня пронизується магнітним потоком, створеним струмом в первинній обмотці. Це дозволяє вважати дріт (разом з вольтметром) обмоткою трансформатора, що має один виток. Для цієї "обмотки" формула трансформатора (2.39) набуває вигляд:
\(\frac{U}{U_{1}}=\frac{1}{N_{1}}\) \(\Rightarrow\) \(N_{1}=\frac{U_{1}}{U}=200\).
Таким чином, первинна обмотка трансформатора складається з N1 = 200 витків. Число витків вторинної обмотки трансформатора N2 також знаходимо з формули (2.40):
\(\frac{U_{1}}{U_{2}}=\frac{N_{1}}{N_{2}}\) \(\Rightarrow\) \(N_{2}=N_{1}\frac{U_{2}}{U_{1}}=6600\),
3. Задачі для самостійної роботи
| 2.10. |
Конденсатор ємністю 1000 пФ зарядили від джерела з ЕРС 100 В і замкнули на котушку індуктивності 10 мкГн. Визначити частоту коливань і максимальну величину енергії котушки WL утвореного контуру. [3,2 МГц; 5 мкДж] |
| 2.11. |
До конденсатора коливального контуру послідовно приєднали ще один такий самий. Як і на скільки змінилася власна частота контуру? [збільшилася на 22,5%] |
| 2.12. |
Коли до конденсатора контуру паралельно приєднали ще один удвічі більшої ємності, частота вільних коливань у контурі змінилася на 300 Гц. Знайти, якою вона була до того. [710 Гц] |
| 2.13. |
У коливальному контурі з індуктивністю 200 мГн амплітуда струму дорівнює 40 мА. Визначити енергію: а) електричного і б) магнітного полів контуру на момент, коли сила струму в ньому складає половину амплітудного значення. [а) 120 мкДж; б) 40 мкДж] |
| 2.14. |
У реальному контурі з ємністю С = 10 мкФ при напрузі на конденсаторі U0 = 400 В починаються вільні коливання. Нехтуючи впливом опору котушки індуктивності R на частоту коливань, визначити кількість теплоти, що виділиться в контурі за час зменшення амплітуди напруги на конденсаторі наполовину. [6 мкДж] |
| 2.15. |
Коливальний контур складається з конденсатора ємністю 0,1 мкФ і котушки індуктивністю 100 мГн. Знайти: а) силу струму в котушці при напрузі на конденсаторі в половину амплітудної Um=1 В і б) напругу на конденсаторі при силі струму в котушці, що складає половину амплітудної Im = 10 мA. [5 мА; 1,5 В] |
| 2.16. |
Ємність одного контуру в 6 разів більша, а індуктивність у 1,5 раза менша, ніж другого. Як співвідносяться енергії W1 : W2 частоти вільних коливань ν1: ν2 у цих контурах при однаковій амплітуді а) напруги на конденсаторі та б) струму в котушці. [W1: W2 = 1 : 1; ν1: ν2 = 1 : 2] |
| 2.17. |
Ємність контуру із власною частотою 480 Гц дорівнює 1,2 мкФ. Визначити амплітуду струму в котушці індуктивності при амплітуді напруги його конденсаторі 15 В. [5,4 мА] |
| 2.18. |
В контурі з ємністю 1 мкФ амплітуда напруги на конденсаторі дорівнює 5 В. Визначити власну частоту контуру, якщо при половинній напрузі на конденсаторі сила струму в котушці складає 27 мА. [9,9 кГц] |
| 2.19. |
При зміні ємності конденсатора на 50 пФ власна частота коливального контуру змінилася від 100 кГц до 120 кГц. Визначити індуктивність його котушки. [15, 5 мГн] |
| 2.20. |
При послідовному приєднанні в коливальному контурі до власного конденсатора ємністю 1,5 мкФ ще одного частота вільних коливань змінилася від 400 Гц до 600 Гц. Визначити ємність приєднаного конденсатора. [1,2 мкФ] |
| 2.21. |
Визначити період вільних коливань у контурі, якщо в ньому при амплітуді струму в котушці 1 мА амплітуда заряду конденсатора складає 10 мкКл [63 мс] |
| 2.22. |
На конденсатор реального коливального контуру ємністю 10 мкФ подали заряд 2 мКл. Знайти кількість теплоти, що виділиться в контурі після початку коливань за час, протягом якого їхня амплітуда зменшиться в 1,5 раза? [111 мДж] |
| 2.23. |
В ідеальному контурі з індуктивністю 200 мГн амплітуда вільних коливань струму дорівнює 40 мА. Визначити енергії електричного та магнітного полів контуру на момент, коли в ньому сила струму складатиме 50% від максимальної. [120 мкДж; 40 мкДж] |
| 2.24. |
У коливальному контурі з ємністю 20 мкФ та індуктивністю 20 мГн у певний момент часу напруга на конденсаторі та сила струму в котушці складають 100 В і 20 мА, відповідно. Визначити заряд на конденсаторі при силі струму в котушці 1 А. [2,3 мКл] |
Розділ ІІІ. Хвилі
|
Термін ''хвиля'' має багато сенсів. У природничих науках хвилями називають поширення в просторі механічних та електромагнітних коливань. Ці хвилі по різному проявляють себе у відчуттях – механічні як звук, а електромагнітні як світло. Але попри це, ті й інші мають спільні загальні властивості й описуються подібними загальними параметрами й рівняннями, котрі розглядаються тут на прикладі механічних хвиль. Що стосується специфічних властивостей світлових хвиль, то їм присвячено частину [5] даного посібника ''ОПТИКА''. Далі розглянуто: 1.Теоретичні відомості 1.1. Рівняння і параметри монохроматичної хвилі 1.2. Хвильові поверхні та промені |
подібними
1. Теоретичні відомості.
|
За узгодженістю між напрямком коливань і напрямком поширення хвилі поділяються на поперечні, де ці напрями є взаємно перпендикулярні, та поздовжні, в яких коливання відбуваються вздовж напрямку поширення. Прикладом поперечних хвиль є електромагнітні, зокрема світлові, хвилі. Натомість механічні, приміром звукові, хвилі всередині якогось середовища є поздвжніми. Проте на поверхні рідини, як добре відомо, спостерігаються поперечні хвилі. Іншою характерною рисою хвилі є вид коливань, які її утворюють. На загал, він може бути складним, але в теорії доведено, що всяку хвилю можна трактувати як суперпозицію (накладання) простих монохроматичних хвиль, в яких коливання є гармонічними (про походження терміну "монохроматичні" див. [5]). Принагідно зауважимо, що згідно з критерєм гармонічних коливань (1.10), механічні монохроматичні хвилі можуть існувати тільки в пружних середовищах. Далі розглянуто: 1. Теоретичні відомості 1.1. Рівняння і параметри монохроматичної хвилі 1.2. Хвильові поверхні та промені 1.3. Звук 2 |
1.1. Рівняння і параметри монохроматичної хвилі
|
Аби з’ясувати, як і від чого залежать властивості монохроматичної хвилі, уявімо нескінченну площину-мембрану, що починає здіснювати гармонічні коливання в однорідному пружному середовищі вздовж осі ОХ, як показано на схематичному рис. 15.1. Залежність $\text{ }\!\!\xi\!\!\text{ }\left( x,t \right)$ легко встановити. Справді, нехай коливання мембрани та прилеглих (x = 0) шарів середовища відбуваються з амплітудою А і періодом за законом |
|
|
|
$\text{ }\!\!\xi\!\!\text{ }\left( 0,t \right)=A\cos \frac{2\text{ }\!\!\pi\!\!\text{ }}{T}t.$ |
|
|
(Примітка. З таким самим успіхом можна використати й функцю sin)
Тоді, врахувавши, що при швидкості поширення хвилі v коливання на відстані x від мембрани почнуться пізнше на час $\tau =(x/v)$, отримаємо наступне рівняння плоскої монохроматичної хвилі:
|
$\text{ }\!\!\xi\!\!\text{ }\left( x,t \right)=A\cos \frac{2\text{ }\!\!\pi\!\!\text{ }}{T}\left( t-\frac{x}{v} \right),$ |
(3.1) |
або через частоти:
|
$\text{ }\!\!\xi\!\!\text{ }\left( x,t \right)=A\cos 2\pi \nu \left( t-\frac{x}{v} \right),$ |
(3.1а) |
|
$\text{ }\!\!\xi\!\!\text{ }\left( x,t \right)=A\cos \omega \left( t-\frac{x}{v} \right).$ |
(3.1б) |
Одразу слід зауважити, що коливаня в хвилі є вимушеними, тож їхнї параметри задаються джерелом. Отже,
|
амплітуда і період, (або циклічна чи лінійна частоти) хвилі не залежать від властивостей середовища. |
Натомість
|
швидкість поширення хвилі визначається тільки її фізичною природою та властивостями середовища |
Як видно з рівнянь (3.1), на заданій відстані від джерела x = x0 шар молекул здійснює коливання за законом
|
$\text{ }\!\!\xi\!\!\text{ }\left( t \right)=A\cos \left( \frac{2\text{ }\!\!\pi\!\!\text{ }}{T}t-{{\text{ }\!\!\varphi\!\!\text{ }}_{0}} \right),$ |
(3.2) |
з періодом T, амплітудою A (рис.15.2а відмітити А) і початковою фазою
|
${{\text{ }\!\!\varphi\!\!\text{ }}_{0}}=\frac{2\text{ }\!\!\pi\!\!\text{ }{{x}_{0}}}{vT}\text{.}$ |
(3.2а). |
Аналогічно розподіляються в просторі й відхилення $\text{ }\!\!\xi\!\!\text{ }$(x) шару молекул від положення рівноваги (рис.15.2б) в будь-який заданий момент часу $t={{t}_{0}}$:
| \(\xi(x)=A\cos\left(\frac{2\pi}{Tv}x-\varphi_{0}^{\prime}\right)\), | (3.3) |
де
|
\(\varphi_{0}^{\prime}=\frac{2\pi{t}_{0}}{T}\). |
(3.3а) |
При цьому значення $\text{ }\!\!\xi\!\!\text{ }$ періодично повторюються в напрямку поширення хвилі на відстані, яка називається довжиною хвилі $\lambda $. Тож, відповідно до рівняння (3.3),
|
$\frac{2\pi }{vT}\left( x+\lambda \right)-\frac{2\pi }{vT}x=2\pi \quad \Rightarrow \quad \lambda =vT$, |
(3.4) |
тобто,
довжина хвилі – це відстань, на яку хвиля поширюється за один період коливань.
При цьому
|
довжина хвилі залежить і від джерела, що задає період коливань, і від середовища, котре визначає швидкість їхнього поширення. |
Довжину хвилі можна виразити також через частоту:
|
$\lambda =\frac{v}{\nu },$ або $\lambda =\frac{2\text{ }\!\!\pi\!\!\text{ }v}{\omega }.$ |
(3.4а) |
Використання параметра λ надає рівнянню (3.1) вигляду:
|
$\text{ }\!\!\xi\!\!\text{ }\left( x,t \right)=A\cos \left( \frac{2\text{ }\!\!\pi\!\!\text{ }}{T}t-\frac{2\text{ }\!\!\pi\!\!\text{ }}{\lambda }x \right)$, |
(3.5) |
який ’’симетрично’’ відображує періодичність хвильового процесу і в часі, і в просторі і є одним із головних параметрів хвилі. Але в теорії замість довжини хвилі зазвичай використовують хвильове число
|
$k=\frac{2\text{ }\!\!\pi\!\!\text{ }}{\lambda }$, |
(3.6) |
що, з урахуванням співвідношення T = (2π/ω), дозволяє найбільш компактно й зручно для викладок записати рівняння (3.5), як
|
$\text{ }\!\!\xi\!\!\text{ }\left( x,t \right)=A\cos \left( \omega t-kx \right).$ |
(3.7) |
Загальні результати, котрі отримано тут для плоскої хвилі, зберігають чинність і для інших типів хвиль, зокрема, сферичних хвиль, які збуджуються точковим джерелом (маленькою вібруючою кулькою) в однорідному ізотропному середовищі. Але, на відміну від плоскої, у сферичній хвилі енергія переноситься не в один бік, а радіально по всіх напрямах від місця розташування джерела. Через це кожна випромінена порція енергії поступово розподіляється по все більшій поверхні, через що амплітуда хвилі в напрямку поширення зменшується пропорційно відстані r до джерела. Отож, рівняння сферичної хвилі має вигляд:
|
$\text{ }\!\!\xi\!\!\text{ }\left( r,t \right)=\frac{A}{r}\cos \left( \omega t-kr \right)$, А = const. |
(3.7а) |
Поширення коливань зумовлює перенесення хвилею енергії, тож і її дію на об'єкти, що перебувають у хвильовому полі. Кількісною мірою перенесення енергії є
інтенсивність хвилі – енергія, що переноситься за одиницю часу через одиницю площі хвильової поверхні, що проходить через дану точку:
|
$I=\frac{\Delta W}{\Delta t\Delta S}$ (Вт/м2) |
(3.8) |
1.2. Хвильові поверхні та промені
Отримані вище результати є чинними не лише для механічних, ф й для інших хвиль. Тому в теорії величина $\xi \left( x,t \right)$ іменують хвильовою функцією, а її аргумент – фазою:
|
\(\varphi=\omega{t}-kx\), |
(3.9) |
|
|
$\varphi =\omega t-kr$, |
(3.9а) |
Просторовий розподіл миттєвих значень хвильової функції наочно відображають за допомогою
хвильових поверхонь: сукупностей точок, в яких фаза хвилі в даний момент часу має одне й те саме значення.
Форму хвильових поверхонь, яка залежить від конфігурації джерела та властивостей середовища, можна визначити, підставивши в рівняння фази задану величину \(\varphi=\varphi_{0}\) та t = t0. Зокрема, з рівнянь (3.8) плоскої та сферичної хвиль в однорідному середовищі виходить:
\(\varphi_{0}=\omega{t}-kx\) \(\Rightarrow\) x = const,
\(\varphi_{0}=\omega{t}-kr\) \(\Rightarrow\) r = const,
тобто, рівняння паралельних площин (рис.15.3а) і концентричних сфер (рис.15.3б), як і має бути.
Окрім хвильових поверхонь, для візуального відображення хвилі також використовують
промені – лінії, вздовж яких енергія від джерела переноситься до різних точок.
Як видно з рис. 15.3, у плоских і сферичних хвилях промені є прямолінійні й скрізь спрямовані по нормалі (ортогонально) до хвильових поверхонь. Така взаємна орієнтація променів і хвильових поверхонь зберігається для хвиль будь-якого типу. Але це не стосується променів, які при іншій конфігураці джерела, або неоднорідному середовищі можуть бути викривленими.
Вище по замовчуванню вважалося, що хвиля займає весь простір. Насправді ж вона починається в місці розташування джерела й на будь-який визначений момент часу добігає точок, які утворюють фронт хвилі. Іншими словами,
фронт хвилі – то є поверхня, що розмежовує хвильову зону та область, куди хвиля ще не дійшла.
Зрозуміло, що, коли джерело перебуває в спокої, фронт хвилі збігається з крайньою хвильовою поверхнею. Але для рухомого джерела це не так. Для ілюстрації розглянемо розповсюдження хвилі від точкового джерела, котре прямолінійно рухається в однорідному середовищі із швидкістю u, що перевищує швидкість поширення хвилі v, прміром, як надзвуковий літак. За такої умови хвильова зона весь час знаходиться позаду джерела й починається в місці його розташування на даний момент (т. О на рис. 15.4).
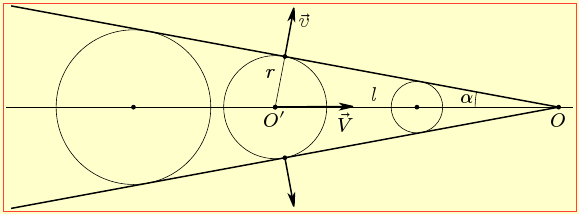
$l=u\tau $,
від джерела вже дійде до поверхні сфери радіуса
$r=v\tau $.
Отже, незалежно від положення т. ${O}'$,
$\frac{r}{v}=\sin \alpha =const$.
Це означає, що фронтом хвилі є бічна поверхня конуса, котра переміщується зі швидкістю хвилі в поперечному до твірної напрямі, розширюючи хвильову зону. Подібний ефект можна бачити, спостерігаючи слід на воді, який лишає за собою рухомий катер.
При русі джерела відносно спостерігача, крім фронту хвилі, змінюється і її частота. Це явище, котре називається ефектом Доплера, детальніше розглянуто далі (п. 2. Приклади розв'язування задач, №№ 1.6, 1.7).
1.3. Звук
Механічні хвилі в деяких інтервалах частот сприймаються живими істотами як звук. Для людини частотний діапазон чутних звуків складає
ν = (16 ÷ 20000) Гц
В інших живих істот цей діапазон є набагато ширший. Тому, хвилі з частотою ν > 20000 Гц називають ультразвуком, а при ν < 16 Гц – інфразвуком. До прикладу, кажани сприймають ультразвуки, через що вухами “бачать” у темряві, а слони ногами “чують” інфразвукові вібрації ґрунту, котрі передаються на дуже великі відстані.
Суб'єктивне сприйняття звуку визначається трьома відчуттями – гучністю, висотою тону та тембром, – з яких перші дві є прямо пов'язані, відповідно, з інтенсивністю та частотою хвилі. А щодо тембру слід сказати таке. Будь-яке джерело, крім основної частоти (тону), випромінює набір супутніх частот меншої інтенсивності, котрий створює притаманне лише йому ''забарвлення'' або ''тембр'' звуку . Ще одним специфічним проявом звуку є ''луна’’ – повторне відчуття звуку внаслідок приходу до місця розташування джерела сигналу, відбитого від віддаленої перешкоди.
На завершення згадаємо ще про один акустичний ефект ''луну’’ – повернення відбитого від перешкоди звукового сигналу до місця розташування джерела.
2. Приклади розв'язування задач
Задача 3.1. У плоскій хвилі, що поширюється зі швидкістю v = 2 м/с, коливання в точці А (рис. 1) відбуваються відповідно до рівняння ${{\xi }_{A}}=5\sin 5\pi t$, см. Визначити зміщення $\xi $ та швидкість коливань u в точках В і С на відстані l1 = 30 см і l2 = 45 см від т. А на момент $\tau$ =1 с.
відбуваються відповідно до рівняння ${{\xi }_{A}}=5\sin 5\pi t$, см. Визначити зміщення $\xi $ та швидкість коливань u в точках В і С на відстані l1 = 30 см і l2 = 45 см від т. А на момент $\tau$ =1 с.
Задача 3.2. Хвилі від катера, що пливе озером, дістаються берега за час t = 0,5 хв і накочуються на нього з інтервалом часу \(\tau=0,8\) с.Визначити відстань L від катера до берега, якщо відстань між гребенями хвиль l = 2 м.
Задача 3.3. Визначити швидкість поширення v монохроматичної хвилі з частотою \(\nu=10\) Гц, якщо на промені в точках на відстані \(\Delta{l}=100\) см одна від одної різниця фаз дорівнює \(\Delta\varphi=\pi/4\).
Задача 3.4. Відстань між гребенями хвиль на морі l = 5 м. Коли катер йде в напрямку поширення хвиль, вони б'ють у ніс катера з частотою n1 = 2 удари за секунду. Якщо ж катер рухається назустріч, то удари йдуть з частотою n2 = 4 удари за секунду. Визначити швидкість поширення хвиль v та швидкість катера V.
Задача 3.5. Літак рухається на висоті H = 4 км з надзвуковою швидкістю. Визначити швидкість V літака, якщо спостерігач на землі почув його через \(\tau= 10\) c після того, як побачив прямо над собою. Швидкість звуку v = 330 м/с.
Задача 3.6. З рухомого потяга подають звуковий сигнал з частотою \(\nu_{0}=400\) Гц. Визначити швидкість V та напрям руху потяга, якщо людина, що вийшла на перон, почула сигнал потяга частотою \(\nu=380\) Гц. Швидкість звуку v = 340 м/с.
Задача 3.7. Сигнальник на залізничному переїзді, повз який пройшов потяг, подає звуковий сигнал частотою \(\nu_{0}=500\) Гц. Визначити швидкість потяга $V$, якщо для машиніста частота сигналу складає ${{\nu }}$ = 470 Гц. Швидкість звуку v = 335 м/с.
Задача 3.8. Два авто, котрі рухаються назустріч із швидкостями ${{v}_{1}}$ = 90 км/год і ${{v}_{2}}$ = 60 км/год, подають звукові сигнали із частотою ${{\nu }_{10}}$ = 400 Гц і ${{\nu }_{20}}$ = 500 Гц, відповідно. Визначити частоту сигналу ${{\nu }_{I}}$ і ${{\nu }_{II}}$, яку сприймає кожен водій при швидкості звуку ${{v}}$ = 340 м/с.
Задача 3.1.
У плоскій хвилі, що поширюється зі швидкістю $v=0,7$ м/с, коливання в точці А (рис. 1) відбуваються відповідно до рівняння ${{\xi }_{A}}=5\sin 5\pi t$, см.
Визначити
зміщення $\xi $ та швидкість коливань u в точках В і С на відстані l1 = 30 см і l2 = 45 см від т. О на момент $\tau$ = 1 с.
|
Дано: ${{\xi }_{A}}=5\sin 5\pi t$, см ${{l}_{1}}=30$см ${{l}_{2}}=45$см
$v=0,7$ м/с
$\tau$ = 1 с |
|
${\xi }_{B,C}$–? |
Розв’язання
В умові рівняння коливань задано в числовій формі, тож їхня амплітуда А = 5 см і частота $\nu = 2,5$ Гц. А позаяк коливання подано через функцією sin, загальне рівняння хвилі (п. 1.1переробити) зручно записати як
зручно записати як
|
|
$\xi \left( x,t \right)=A\sin \left( 2\pi \nu \left( t-\frac{x}{v} \right) \right)$. |
(1) |
|
$\xi =\text{A}\sin \left( 2\pi \nu \left( \tau -\frac{l}{v} \right) \right)$. |
(1а) |
Швидкість коливань, яка є похідною зміщення по часу: $u={\xi }'\left( t \right)$, згідно з рівнянням (1) визначається як
|
$u\left( x,t \right)=2\pi \nu A\cos \left( 2\pi \nu \left( t-\frac{x}{v} \right) \right)$, |
(2) |
і при х = l та t = τ складає:
|
$u=2\pi \nu A\cos \left( 2\pi \nu \left( \tau -\frac{l}{v} \right) \right)$. |
(2а) |
Відтак, підставивши у вирази (1а) і (2а) задані числові дані, отримуємо наступні відповіді:
${\xi }_{1}$ = 2,1 см; ${\xi }_{2}$ = –3,1 см/с.
${{u}_{1}}$ = –71,1 см/с; ${{u}_{2}}$ = 61,4 см/с.
Знаки в отриманих відповідях свідчать про те, що частинки середовища в заданий момент часу й на заданих відстанях від точки А знаходяться по різний бік від положення рівноваги й наближаються до нього.
Задача 3.2.
Хвилі від катера, що пливе озером, дістаються берега за час t = 0,5 хв і накочуються на нього з інтервалом часу \(\tau=0,8\) с.
Визначити
відстань L від катера до берега, якщо відстань між гребенями хвиль l = 2 м.
|
Дано: t = 30 c
l = 2 м
\(\tau=0,8\) с
|
|
L - ?
|
Розв’язання
За час \(\tau\) між послідовними ударами в берег хвиль від катера вони переміщуються на відстань l, отже, поширюються зі швидкістю
\(v=\frac{l}{\tau}\).
У такому разі відстань від катера до берега, яку хвилі долають за час t, становить
\(L=vt=\frac{l}{\tau}t=\frac{2}{0,8}\cdot{30}= 75\) м.
Задача 3.3.
Визначити
швидкість поширення v монохроматичної хвилі з частотою \(\nu=10\) Гц, якщо на промені в точках на відстані \(\Delta{l}=100\) см одна від одної різниця фаз дорівнює \(\Delta\varphi=\pi/4\).
|
Дано: \(\nu=10\) Гц \(\Delta{l}=100\) см \(\Delta\varphi=\pi/4\) |
|
v – ? |
Розв'язання
Відповідно до формули (3.9) можна записати:
|
|
\(\Delta\varphi=\frac{2\pi}{\lambda}\Delta{l}\), |
(1) |
де \(\Delta{l}\) – задана відстань між точками, \(\lambda\) – довжина хвилі.
Швидкість поширення хвилі v виражається через довжину хвилі на основі формули (3.4a):
|
|
\(v=\lambda\nu\), |
(2) |
Виразивши величину l з співвідношення (1) і підставивши її у формулу (2), дістанемо
\(v=\frac{2\pi\nu\Delta{l}}{\Delta\varphi}= 80\) м/с.
Задача 3.4.
Відстань між гребенями хвиль на морі l = 5 м. Коли катер йде в напрямку поширення хвиль, вони б'ють у ніс катера з частотою n1 = 2 удари за секунду. Якщо ж катер рухається назустріч, то удари йдуть з частотою n2 = 4 удари за секунду.
Визначити
швидкість поширення хвиль v та швидкість катера V.
|
Дано: l = 5 м
\(n_{1}=2\)
\(n_{2}=4\)
|
|
v, V - ? |
Розв’язання
Відстань між гребенями l – це довжина хвилі, а кількість ударів об корпус дорівнює частоті коливань для рухомого спостерігача, що знаходиться на катері. Отже згідно з формулою (3.4a) можна записати:
|
|
n1l = v1, |
(1) |
|
N2l = v2, |
(2) |
де v1, v2 – швидкості поширення хвиль відносно катера у випадках руху вздовж та проти напрямку поширення хвиль. Згідно з законом додавання швидкостей (1.9)
v1 = V – v;
v2 = V + v,
де V, v – швидкості руху катера та поширення хвиль відносно води.
Підставивши сюди вирази (1), (2) для швидкостей і розв'язавши отриману систему, дістанемо відповіді:
\(\left.\begin{align} {}n_{1}l=V-v \\ {}n_{2}l=V+v \\ \end{align}\right\}\) \(\Rightarrow\) \( \begin{align} {}V=l\frac{n_{1}+n_{2}}{2}=15\ {м/с}; \\ {}v=l\frac{n_{2}-n_{1}}{2}=5\ {м/с}. \\ \end{align}\)
Задача 3.5.
Літак рухається на висоті H = 4 км з надзвуковою швидкістю .
Визначити
швидкість V літака, якщо спостерігач на землі почув його через \(\tau= 10\) c після того, як побачив прямо над собою. Швидкість звуку v = 330 м/с.
|
Дано: H = 4 км = 4000 м
\(\tau= 10\) c
v = 330 м/с
|
|
V - ?
|
Розв’язання
При надзвуковій швидкості фронт звукової хвилі від літака має форму конуса з вершиною в місці його розташування і кутом між віссю та твірною, що визначається співвідношенням швидкостей звуку та літака (див. п. 1.2). На схематичному рисунку показано напрям руху літака OD та ділянки АВ і СD твірних фронту звукової хвилі на моменти, коли спостерігач з точи С побачив літак і почув його звук, відповідно. Тож, як видно, за час \(\tau\) літак пролетів відстань BD рівну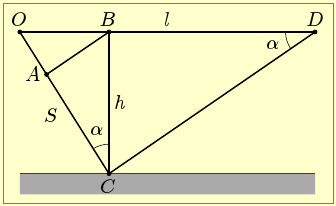
\(l=V\tau\),
а звук поширився на відстань AC, що складає
\(s=v\tau\).
Отже,
$V=\frac{l}{s}\cdot v$ (1)
Таким чином, задача зводиться до визначення відстані l, що легко зробити, врахувавши подібність трикутників ΔАВС і ΔВСD та теорему Піфагора. А саме,
$\frac{l}{s}=\frac{h}{\sqrt{{{h}^{2}}-{{\left( v\tau \right)}^{2}}}}=\frac{1}{\sqrt{1-{{\left( \frac{v\tau }{h} \right)}^{2}}}}$
Відтак із виразу (1) отримуємо відповідь:
$V=\frac{v}{\sqrt{1-{{\left( \frac{v\tau }{h} \right)}^{2}}}}$
Обчислення дають:
V ≈ 2100 км/год
Задача 3.6.
Із рухомого потяга подають звуковий сигнал з частотою \(\nu_{0}=400\) Гц.
Визначити
швидкість V та напрям руху потяга, якщо людина, що вийшла на перон, почула сигнал потяга частотою \(\nu=380\) Гц. Швидкість звуку v = 340 м/с.
|
Дано: $\nu_{0}$ = 400Гц $\nu$ = 380 Гц v = 340 м/с |
| V – ? |
Розв’язання
Приступаючи до розв'язання цієї та подібних задач, слід чітко усвідомити, що в теорії (п. 1.1) при визначенні рівняння та параметрів хвилі по замовчуванню приймається, що джерело і спостерігач є нерухомі відносно середовища, в якому поширюється хвиля. За таких умов частоти коливань, які сприймає спостерігач і створює джерело, збігаються, а швидкість їхнього поширення визначається тільки властивостями середовища і є табличною величиною. 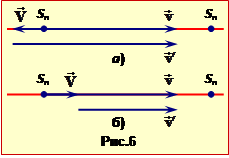 Але коли джерело, спостерігач, або обоє рухаються, характеристики хвилі змінюються. Зокрема, для спостерігача на пероні (точка Sп на рис. 6) частота звукової хвилі \(\nu\) буде відмінною від частоти \(\nu_{0}\) коливань, які створює джерело звуку в рухомому електровозі (точка Sд виправити). Це можна пояснити наступним чином.
Але коли джерело, спостерігач, або обоє рухаються, характеристики хвилі змінюються. Зокрема, для спостерігача на пероні (точка Sп на рис. 6) частота звукової хвилі \(\nu\) буде відмінною від частоти \(\nu_{0}\) коливань, які створює джерело звуку в рухомому електровозі (точка Sд виправити). Це можна пояснити наступним чином.
При нерухомих джерелі та спостерігачі частота хвилі задовольняє співвідношення (3.4a):
|
|
${{\nu }_{0}}=\frac{v}{{{\lambda }_{0}}}$, |
(1) |
в якому довжина хвилі ${{\lambda }_{0}}$ = vT0 – то є відстань між її сусідніми "гребенями" (точками найбільшого стиснення, чи розрідження повітря), а T0 = (1/\(\nu_{0})\)$v$ – час її проходження хвилею, який задається нерухомим джерелом. Але при рухомому джерелі вказана відстань ${{\lambda }}$ ≠ ${{\lambda }_{0}}$. Дійсно, коли джерело рухається із швидкістю V, то на момент виходу з нього якогось гребеня хвилі попередній перемістився на відстань l0 = vT0, а джерело – на відстань lд = VT0 у тому, чи іншому напрямку. Тож відстань між гребенями дорівнє
\(\lambda\)= $\left( v\pm V \right)$T0,
де знак ''+'' відповідає віддаленню, а ''–'' зближенню електровоза та спостерігача. Отже, спостерігач чутиме звук із частотою
|
|
$\nu =\frac{v}{v\pm V}{{\nu }_{0}}$, |
(2) |
За умовою $\nu <{{\nu }_{0}}$, отже в знаменнику виразу (2) має стояти знак ''+'':
|
|
$\nu =\left( \frac{v}{v+V} \right){{\nu }_{0}}$, |
|
тобто електровоз віддаляється від пасажира.
Відтак із виразу (2) після елементарних викладок отримаємо наступну загальнувіповідь:
$V=\left( \frac{{{\nu }_{0}}}{\nu }-1 \right)v$,
і в числах
\(V\) = 64,4 км/год.
Задача 3.7. Сигнальник на залізничному переїзді, повз який пройшов потяг, подає звуковий сигнал частотою \(\nu_{0}=500\) Гц.
Визначити
швидкість потяга $V$, якщо для машиніста частота сигналу складає ${{\nu }}$ = 470 Гц. Швидкість звуку v = 335 м/с.
|
Дано: ${{\nu }_{0}}$ = 500 Гц ${{\nu }}$ = 470 Гц v = 335 м/с |
|
$V$ – ? |
Розв'язання
Ця задача є споріднена із попередньою, але відрізняється тим, що нерухомим є джерело (сигнальник), а не машиніст (спостерігач). За такої умови для обох довжина хвилі $\lambda $ (відстань, яку її гребені проходять за час одного періоду ${{T}_{0}}=\left( 1/{{\nu }_{0}} \right)$ є однаковою й рівною (формула (3.4а)):
$\lambda =\frac{v}{{{\nu }_{0}}}$. (1)
Але відносно машиніста гребені звукової хвилі рухаються зі швидкістю не $v$, ${v}'=v-V$ (див. [І], розділ І, ф-ла(1.10а)), і частота звуку для нього задовольняє співвідношення
$\lambda =\frac{v-V}{\nu }$. (2)
Отож, прирівнявши праві частини виразів (1) і (2), після елементарних викладок дістанемо наступну загальну та числову вдповіді задачі:
$V=\left( 1-\frac{\nu }{{{\nu }_{0}}} \right)v$ = 72,4 км/год.
Задача 3.8. Два авто, котрі рухаються назустріч зі швидкостями ${{v}_{1}}$ = 90 км/год і ${{v}_{2}}$ = 60 км/год, подають звукові сигнали із частотою ${{\nu }_{10}}$ = 400 Гц і ${{\nu }_{20}}$ = 500 Гц, відповідно.
Визначити
частоту сигналу ${{\nu }_{I}}$ і ${{\nu }_{II}}$, яку сприймає кожен водій при швидкості звуку ${{v}}$ = 340 м/с.
|
Дано: ${{v}_{1}}$ = 90 км/год ${{v}_{1}}$ = 60 км/год ${{\nu }_{10}}$ = 400 Гц ${{\nu }_{10}}$ = 500 Гц ${{v}}$ = 340 м/с |
|
${{\nu }_{I}}$ – ? ${{\nu }_{II}}$– ? |
Розв'язання
Відповідно до умови, кожен водій є рухомим спостерігачем, який сприймає звук від рухомого джерела. Інакше кажучи, ця задача за змістом є об'єднанням двох попередніх. Отож, аби перший водій не рухався, то для нього у відповідності до формули (2) із задачі 3.6 частота сигналу складала би
${{\nu }^{*}}=\frac{v}{v-{{v}_{2}}}{{\nu }_{20}}$.
Але через рух із швидкістю ${{v}_{1}}$ назустріч джерелу (другому автомобілю) вона, згідно з формулою (2) із задачі 3.7, є більшою в $\left( v+{{v}_{1}} \right)/v$ разів і насправді дорівнює
${{\nu }_{I}}=\frac{v+{{v}_{1}}}{v-{{v}_{2}}}{{\nu }_{20}}$.
Рух як такий є відносним, тож, помінявши у цьому виразі порядок індексів, отримаємо й другу відповідь:
${{\nu }_{II}}=\frac{v+{{v}_{2}}}{v-{{v}_{1}}}{{\nu }_{10}}$.
Обчислення (не забудьте первести швидкості авто в {м/с}) дають:
${{\nu }_{I}}$ = 564 Гц; ${{\nu }_{II}}$ = 453 Гц.
На завершення варто зазначити, що розглянута в останніх прикладах варіативність частоти хвилі зумовлюється відносним рухом спостерігача та джерела і є притаманна також електромагнітним, зокрема, світловим хвилям. Вона називається ефектом Доплера по імені австрійського вченого, котрий її відкрив і пояснив. (Аби побачити один із проявів ефекту Доплера, клікніть тут)
3. Задачі для самостійної роботи
При розгляді механічних хвиль, зокрема звукових, потрібно пам'ятати, що швидкість поширення хвилі і швидкість руху часток середовища – це різні швидкості. Перша визначається фізичними властивостями середовища, а друга – амплітудою і частотою хвилі.
В умовах задач по замовчуванню прийнято, що хвилі є плоскими, створюються джерелом, яке розміщено в початку координат, і поширюються вздовж осі ОХ без утрат енергії.
Наведені відповіді отримано при g = 10 м/с2.
|
Рівень А |
|
|
Рівняння хвилі має вигляд: $\xi \left( x,t \right)=3\sin \left( 3\pi \left( t-0,5x \right) \right)$, см. Записати її частоту (Гц) і швидкість поширення (м/с). [1,5 Гц; 2 м/с] |
|
|
У хвилi, що поширюється зі швидкістю 1,2 м/с, коливання в початку координат визначаються рiвнянням $\xi \left( 0,t \right)=3\sin 2\pi t$ (см). Визначити величину та напрям зміщення частинок середовища $\xi$ у початковий момент часу на відстані l = 11 м. [–2,6 см] |
|
|
У хвилі з частотою 500 Гц і амплітудою 5 мкм, яка поширюється зі швидкістю 340 м/с, коливання відбуваються за законом косинуса з нульовою початковою фазою. Визначити зміщення з положення рівноваги, швидкість і прискорення частинок середовища на відстані 170 м у момент часу \(t=1\) c. [5 мкм; 0; –49 см/с2] |
|
| 3.12. |
Визначити швидкicть поширення хвилi з частотою 10 Гц, в якій на вiдcтані 1 м фаза змінюється на (π/4). [80 м/с] |
| 3.13. |
Хвиля на воді з частотою 2 Гц поширюється зі швидкістю 2,4 м/с. Визначити її різницю фаз у двох точках, що в напрямку поширення віддалені одна від одної на 10 см, 60 см, та 90 см. [0,52 рад; 3,14 рад; 4,7 рад] |
|
Хвиля від човна дістається берега за 0,5 хв. На якій відстані від берега він знаходиться, якщо гребені хвилі є віддалені 1,5 м один від одного й накочують на берег з інтервалом 1 с? [45 м] |
|
|
Рибалка помітив, що за 10 с поплавець здійснює 20 коливань на хвилях, відстань між гребенями котрих дорівнює 1,2 м. Визначити, з якою швидкістю хвилі накочують на берег. [2,4 м/с] |
|
|
Хвилі накочують на берег водойми зі швидкістю 1 м/с. З якою частотою хвилі вдаряють у берег, якщо відстань між їхніми гребенями дорівнює 1,25 м? [4 удари за 5 с] |
|
| 3.17. |
Стрілець почув відлуння після пострілу по мішені через 0,52 с. Нехтуючи опором повітря, знайти відстань до мішені, якщо швидкість вильоту кулі та шіидкість звуку складали 45о м/с і 335 м/с, відповідно? [100 м] |
|
Визначити швидкість вильоту кулі зі ствола рушниці при вертикальному пострілі, якщо вона та звук пострілу одночасно досягли висоти 680 м. [350 м/с] |
|
|
Пароплав поблизу пристані подає звуковий сигнал з частотою 400 Гц. З якою швидкістю і в якому напрямі рухається пароплав, якщо для спостерігача на причалі вона складає 406 Гц? [5 м/с; причалює] |
Рівень B
|
3.20. |
У деякій точці поздовжньої хвилі, що поширюється зі швидкістю 60 cм/с, коливання відбуваються за законом $\xi =5\cos 20\text{ }\!\!\pi\!\!\text{ }t$ (мм). Знайити фазу хвилі та величину $\xi $ у початковий момент на відстані 11 м від указаної точки в напрямку поширення хвилі. [0,58 рад; –1,3 см] |
|
3.21. |
Відстань між гребенями хвиль у морі становить 5 м. Коли катер рухається проти вітру, то хвилі вдаряють у корпус 4 рази за секунду, а при рухові за вітром – 2 рази. Визначити швидкості катера та хвилі. [15 м/с; 5 м/с] |
|
3.22. |
Дві точки на напрямку поширення хвилі з частотою 10 Гц є віддалені одна від одної на 1 м. Визначити швидкість поширення хвилі, якщо різниця її фаз у цих точках складає π/4 рад. [80 м/с] |
|
3.23. |
Довжина хвилі в першому середовищі складає \(\lambda\), а в другому –\(k\lambda\). Як зміниться швидкість поширення хвилі при переході з першого середовища в друге, якщо \(k=2\)? [зросте 2 рази] |
|
3.24. |
Електричка, котра рухається зі швидкістю 72 км/год, подає звуковий сигнал частотою 390 Гц. Яку частоту сприймає пасажир у зустрічній електричці, що має швидкість 60 км/год? Швидкість звуку 335 м/с. [435 Гц] |
|
3.25. |
Два автомобілі, що рухаються в один бік зі швидкостями 60 км/год і 90 км/год, подають звукові сигнали перший з частотою 500 Гц, а другий 400 Гц. Визначити частоту сигналу для кожного водія, коли перший: а) наздоганяє другого; б) відстає від нього. [а) ν1 = 451,6 Гц, ν2 = 566,1 Гц; б) ν1 = 391 Гц, ν2 = 487 Гц] |