ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
2. Приклади розв'язування задач
2.2. Змінний струм
У наведених задачах розглядаються тільки синусоїдальні напруги та струми, і в умовах, якщо не вказано інше, фігурують діючі (''ефективні'') значення цих величин. Окрім того, конденсатори й котушки індуктивності по замовчуванню вважаються ідеальними.
Задача 2.4. При подачі на газорозрядну лампу змінної напруги вона загоряється й гасне, коли напруга на електродах сягає заданої величини Uз (''напруги загоряння''). Знайти, який відсоток часу ввімкнення \(\eta\) горить лампа при напрузі U = Uз.
Задача 2.5. У мережу змінного струму ввімкнено ланцюжок із послідовно з'єднаних резистора R = 100 Ом і двох запаралелених конденсаторів по C = 30 мкФ. Визначити відношення сил струму в ланцюжку до (I1) та після (I2) пробою одного з конденсаторів.
Задача 2.6. Сила струму в котушці з індуктивністю L = 30 мГн при підключенні до батареї з малим внутрішнім опором і ЕРС \({\E}\) = 9 В складає I1 = 1 A. Якою вона буде, якщо на котушку подати змінну напругу \(U={\E}\) промислової частоти $\nu $ = 50 Гц?
Задача 2.7. Послідовно з'єднані конденсатор змінної ємності С, котушку індуктивності L = 340 мГн і резистор R = 2 Ом увімкнено в мережу з напругою U = 220 В і частотою [\{\nu}=50\)Гц. Визначити: А) величину C, при якій струм у колі буде максимальним; Б) напругу UC, UL і UR на кожній ділянці за такої умови.
Задача 2.8. Послідовний ланцюг із котушки індуктивності L = 6 мкГн, конденсатора С = 0,01 мкФ і резистора R = 0,5 Ом підключено до генератора з регульованою частотою. Визначити потужність P, що виділяється в ланцюзі при резонансній частоті й амплітуді напруги на конденсаторі ${{U}_{mc}}$= 10В.
Задача 2.9. Обмотки трансформатора, що підвищує напругу від U1 = 100 В до U2 = 3300 В, намотано на кільцевому осерді. Визначити кількості витків N1 і N2 в обмотках, якщо при підключенні до вольтметра пропущеної крізь осердя дротини він показує U = 0,5В.
Задача 2.4
При подачі на газорозрядну лампу змінної напруги вона загоряється й гасне, коли напруга на електродах сягає заданої величини Uз (''напруги загоряння'').
Знайти
який відсоток часу ввімкнення \(\eta\) горить лампа при напрузі U = Uз.
|
Дано: \(U=U_{з}\)
|
|
\(\eta\) - ?
|
Розв’язання
За означенням (2.36) та умовою задачі, напруга загоряння лампи складає
| \(U_{з}\) = \(\frac{U_{m}}{\sqrt{2}}\), |
(1) |
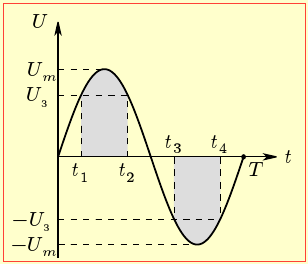
де \(U_{m}\) – амплітуда подаваної напруги. При цьому поточне значення напруги на лампі u(t) визначається рівнянням (2.17):
| u(t) = \(U_{m}\sin\omega{t}\) |
(2) |
Отже, як видно з рис. 8, лампа в кожен період T горить на протязі інтервалу часу
| \(\tau=T-4t_{1}\) |
(1) |
де t1 — проміжок часу, за який напруга на лампі змінюється від 0 до \(U_{з}\) і навпаки. Отже, згідно з виразами (1) і (2),
\(\sin\omega{t}_{1}=\frac{1}{\sqrt{2}}\) \(\Rightarrow\) \(\omega{t}_{1}=\frac{\pi}{4}\).
Звідси, врахувавши зв'язок між частотою та періодом (1.3), знайдемо величину t1:
\(\frac{2\pi}{T}t_{1}=\frac{\pi}{4}\) \(\Rightarrow\) \(t_{1}=\frac{T}{8}\),
та відповідь
\(\tau=T-4\frac{T}{8}=\frac{T}{2}\) \(\Rightarrow\) \(\eta=\frac{\tau}{T}=0,5=50\) %.
Отже, лампа горітиме половину часу перебування під напругою.
Задача 2.5
У мережу змінного струму ввімкнено ланцюжок із послідовно з'єднаних резистора R = 100 Ом і двох конденсаторів по C = 30 мкФ (рис. 9а).
Визначити
відношення сил струму в ланцюжку до (I1) та після (I2) пробою одного з конденсаторів.
|
Дано: \(\nu\) = 50 Гц
R = 100 Ом
C = 30 мкФ = 3·10-5 Ф
|
|
\((I_{1}/I_{2})\) - ?
|
Розв’язання
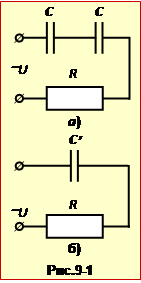При електричному пробої діелектрика в конденсаторі утворюється провідний канал, який ''закорочує'' (сполучає між собою) його пластини. Тож, замість первісного (рис. 9а), утворюється новий ланцюг (рис. 9б) із тією самою поданою напругою. Тому за законом Ома (2.29)
${{I}_{1}}{{Z}_{1}}={{I}_{2}}{{Z}_{2}}\quad \Rightarrow \quad $\(\frac{I_{1}}{I_{2}}=\frac{Z_{2}}{Z_{1}}\), (1)
де Z – імпеданс (повний опір) ланцюжка (2.30), який за відсутності котушки індуктивності дорівнбє:
$Z=\sqrt{{{R}^{2}}+X_{c}^{2}}$
При цьому в першому випадку ємність ланцюга за формулою ([3], (1.28а)), дорівнює С1 = (C/2), а в другому С2 = С. Отож, відповідно до виразу (2.23), маємо:
\(Z_{1}=\sqrt{R^{2}+\left(\frac{1}{2\pi\nu(C/2)}\right)^{2}}\) = 234,6 Ом.
\(Z_{2}=\sqrt{R^{2}+\left(\frac{1}{2\pi\nu{C}}\right)^{2}}\) =145,8 Ом.
Відтак із співвідношеня (1), отримуємо відповідь:
\(\frac{I_{1}}{I_{2}}\)\(\approx{0,62}\),
тобто сила струму після пробою збільшиться в \(\approx{1,6}\) раза.
Задача 2.6
Сила струму в котушці з індуктивністю L = 30 мГн при підключенні до батареї з малим внутрішнім опором і ЕРС \({\E}\) = 9 В складає I1 = 1 A.
Якою вона буде,
якщо на котушку подати змінну напругу \(U={\E}\) промислової частоти $\nu $ = 50 Гц?
|
Дано: L = 0,03 Гн
\({\E}\) = 9 В
\(I_{1}\) = 1 A
$\nu $ = 50 Гц
|
|
I2 - ?
|
Розв’язання
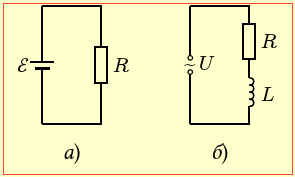
В першому випадку в котушці тече постійний струм, величина якого залежить тільки від активного опору R (опору дроту, яким намотано котушку) і ЕРС джерела. Еквівалентну схему кола для цього випадку показано на рис.10а. Якщо ж струм є змінним, то повний опір кола визначається не тільки опором дроту R, а й індуктивністним опором котушки XL (рис.10б). Отже, відповідно до закону Ома для постійного ([3], (2.10)) та змінного (2.30) струму маємо:
|
|
\(I_{1}=\frac{{\E}}{R}\), \(I_{2}=\frac{U}{Z}\). |
(1) |
Звідси, з урахуванням умови \(U={\E}\), одержуємо:
|
|
\(\frac{I_{2}}{I_{1}}=\frac{R}{Z}\) \(\Rightarrow\) \(I_{2}=I_{1}\frac{R}{Z}\), |
(2) |
де Z – імпенданс (повний опір) котушки. Оскільки в колі немає конденсатора, то опір ємності XC = 0, і з формул (2.31) і (2.28) випливає, що
\(Z=\sqrt{R^{2}+(2\pi\nu{L})^{2}}\).
Підставивши цей вираз у формулу (2), дістанемо:
|
|
\(I_{2}=I_{1}\frac{R}{\sqrt{R^{2}+(2\pi\nu{L})^{2}}}\) = \(I_{1}\frac{1}{\sqrt{1+\left(2\pi\nu{L}/{R}\right)^{2}}}\). |
(3) |
Із формули (1) \(R={\E}/I_{1}\), отже, остаточна відповідь має вигляд:
\(I_{2}=\frac{1}{\sqrt{1/I_{1}^{2}+\left(2\pi\nu{L}/{\E}\right)^{2}}}\).
Обчисленнядають
I2 = 0,7 A.
Задача 2.7
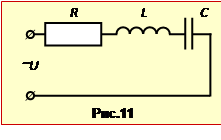Послідовно з'єднані конденсатор змінної ємності С, котушку індуктивності L = 340 мГн і резистор R = 2 Ом увімкнено в мережу з напругою U = 220 В і частотою \(\nu=50\) Гц.
Визначити:
А) величину C, при якій струм у колі буде максимальним; Б) напругу UC, UL і UR на кожній ділянці за такої умови.
|
Дано: L = 340 Гн
R = 2 Ом
\(\nu=50\) Гц
|
|
C - ?
UC, UL , UR - ?
|
Розв’язання
А) Згідно з вирзами (2.29) і (2.31), струм у колі буде найбільшим за умовиови Х = 0, тобто
\(\omega{L}-\frac{1}{\omega{C}}=0\) \(\Rightarrow\) \(\omega{L}=\frac{1}{\omega{C}}\).
Звідси знаходимо:
$C=\frac{1}{{{\omega }^{2}}L}=\frac{1}{{{(2\pi \nu )}^{2}}L}$ = 30 мкФ.
Б) За законом Ома (2.37) при Z = R маємо:
\(I_{m}=\frac{U}{R}\).
Підставивши цей вираз у формули (2.25) і (2.28), знаходимо:
\(U_{C}=\frac{I}{\omega{C}}=\frac{U}{2\pi\nu{CR}}=1061\) В;
\(U_{L}=I\omega{L}=\frac{U}{R}2\pi\nu{L}=1061\) В.
В отриманих результатах впадає в очі здавалося б парадоксальний факт – напруги на конденсаторі і котушці майже в 5 разів перевищують напругу джерела, а напруга на резисторі дорівнює напрузі джерела так, ніби конденсатора і котушки у колі немає. Це пояснюється тим, що напруги на конденсаторі й котушці, що завжди є протилежними за фазою, при резоненсі мають однакову величину.
Задача 2.8
Послідовний ланцюг із котушки індуктивності L = 6 мкГн, конденсатора С = 0,01 мкФ і резистора R = 0,5 Ом підключено до генератора з регульованою частотою (рис. 12).
Визначити
потужність P, що виділяється в ланцюзі при резонансній часоті й амплітуді напруги на конденсаторі UрС = 10 В.
Примітка. Для змінного струму слово "потужність" без спеціальних указівок означає середню потужність за період.
|
Дано: L = 6 мкГн = 6·10-6 Гн
С = 0,01 мкФ = 10-8 Ф
R = 0,5 Ом
${{U}_{mc}}$= 10 В
|
|
P - ?
|
Розв’язання
В колі змінного струму енергію споживає тільки на активному опорі. Тому шукана потужність визначається через резонансну амплітуду сили струму ${{I}_{m}}$ та заданий опір резистора формулою (2.35):
|
\(P=\frac{1}{2}I_{m}^{2}R\), |
(1) |
Позаяк усі елементи ланцюга є з'єднані послідовно, потрібну величину ${{I}_{m}}$ знаходимо за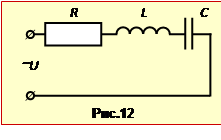 
законом Ома (2.25) через задану амплітуду напруги та опір конденсатора (2.23) при резонансній частоті (2.32):
${{I}_{m}}=\frac{{{U}_{m}}C}{\sqrt{LC}}\quad \Rightarrow \quad {{I}_{m}}={{U}_{mc}}\sqrt{\frac{C}{L}}$.
Підставивши цей вираз у формулу (1), отримаємо відповідь:
$P=\frac{U_{mc}^{2}RC}{2L}\approx$41,7 мВт.
Задача 2.9
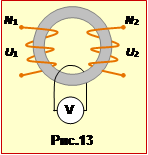Обмотки трансформатора, що підвищує напругу від U1 = 100 В до U2 = 3300 В, намотано на кільцевому осерді (рис.13).
Визначити
кількості N1 і N2 витків у обмотках, якщо при підключенні до вольтметра пропущеної крізь осердя дротини він показує U = 0,5 В.
|
Дано: \(U_{1}\) = 100 В
\(U_{2}\) = 3300 В
\(U\) = 0,5 В
|
|
N1, N2 - ?
|
Розв’язання
Дріт разом з вольтметром утворюють замкнутий контур. Його поверхня пронизується магнітним потоком, створеним струмом в первинній обмотці. Це дозволяє вважати дріт (разом з вольтметром) обмоткою трансформатора, що має один виток. Для цієї "обмотки" формула трансформатора (2.39) набуває вигляд:
\(\frac{U}{U_{1}}=\frac{1}{N_{1}}\) \(\Rightarrow\) \(N_{1}=\frac{U_{1}}{U}=200\).
Таким чином, первинна обмотка трансформатора складається з N1 = 200 витків. Число витків вторинної обмотки трансформатора N2 також знаходимо з формули (2.40):
\(\frac{U_{1}}{U_{2}}=\frac{N_{1}}{N_{2}}\) \(\Rightarrow\) \(N_{2}=N_{1}\frac{U_{2}}{U_{1}}=6600\),