ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
1. Теоретичні відомості
1.2. Змінний струм
|
Змінним струмом називаються вимушені коливання в електричному колі, підключеному до джерела ЕРС якого періодично змінюється з часом. В елементарній фізиці розглядаються тільки синусоїдальні змінні струми. Такі струми повсюдно використовуються в електротехніці та побуті. Але в електроніці широко застосовують й інші змінні струми. У загальному випадку коло змінного струму, крім джерела (генератора) та резисторів, містить конденсатори і котушки індуктивності, котрі теж мають свій опір. Тому в колах змінного струму вирізняють активний і реактивні ємнісний та індуктивний опори. Тож зв'язок між струмом і напругою (ЕРС) генератора визначається повним опором кола і описується законом Ома для змінного струму. За певних умов у колах змінного струму спостерігається резонанс – явище, котре має важливі практичні застосування. Потужність змінного струму залежить не тільки від напруги і сили струму, але й від різниці фаз коливань цих величин. Специфічним для кіл змінного струму є також використання трансформаторів – пристроїв для перетворення напруги та сили струму. |
Серед різноманітних змінних струмів найпростішим є синусоїдальний струм, який створюється генератором із напругою (ЕРС)
|
|
\(u=U_{m}\sin\omega{t}\), |
(2.17) |
або
|
$u={{U}_{m}}\cos \left( \omega t-\frac{\pi }{2} \right)$, |
(2.17а) |
де Um – амплітуда, \(\omega\) – циклічна частота (рад/с).
У техніці змінний струм характеризують лінійною частотою
$\nu =\frac{\omega }{2\pi }$ (Гц)
![]()
Генератор змінного струму на електричних схемах зображують так:
 Активним опором R (рис.14.4) називають опір резистора в колі змінного струму. Він, як і при постійному струмі, є зумовлений гальмуванням упорядкованого руху носіїв струму іншими частинками провідника. Тож для змінного струму в резисторах є дійсними всі закони постійного струму, зокрема закон Ома:
Активним опором R (рис.14.4) називають опір резистора в колі змінного струму. Він, як і при постійному струмі, є зумовлений гальмуванням упорядкованого руху носіїв струму іншими частинками провідника. Тож для змінного струму в резисторах є дійсними всі закони постійного струму, зокрема закон Ома:
|
\(i=\frac{u}{R}\), |
(2.18) |
де i та u – миттєві значення сили струму і напруги на резисторі, R – його опір. Отож, якщо на резистор подати напругу, що змінюється за законом (2.17), струм у ньому буде змінюватися так само:
|
|
\(i=I_{m}\sin\omega{t}\), |
(2.19) |
де амплітуда
|
|
\(I_{m}=\frac{U_{m}}{R}\). |
(2.20) |
 Ємнісним опором називається опір, що створюється в колі змінного струму ідеальним конденсатором.
Ємнісним опором називається опір, що створюється в колі змінного струму ідеальним конденсатором.
Напруга на конденсаторі кожної миті дорівнює напрузі генератора (формула (2.17)), до якого він підключений (рис.14.5). Отже, заряд конденсатора q = Cu змінюється з часом за законом
|
\(q=CU_{m}\sin\omega{t}\). |
(2.21) |
При цьому через з'єднувальні провідники і генератор протікає струм, який називається струмом конденсатора і, позаяк за означенням і = q′ ([ІІІ], ф-ла (2.2)), складає:
|
|
\(i=\omega{C}U_{m}\cos\omega{t}\), |
(2.22) |
або
|
|
\(i=I_{m}\sin\left(\omega{t}+\frac{\pi}{2}\right)\), |
(2.22a) |
де ${{I}_{m}}=\omega C{{U}_{m}}$ – амплітуда струму.
(Зауважимо, що струм конденсатора – абстрактне поняття, адже він зумовлюється не рухом зарядів між обкладками конденсатора, а зміною напруги на ньому.)
По аналогії з виразом (2.20) амплітуду струму конденсатора можна записати, як
|
\(I_{m}=\frac{U_{m}}{(1/\omega{C})}\). |
(2.23) |
Отже, струм конденсатора при заданій напрузі обмежується величиною
|
|
\(X_{C}=\frac{1}{\omega{C}}=\frac{1}{2\pi\nu{C}}\), |
(2.24) |
яка називається ємнісним опором.
Таким чином, для змінного струму в конденсаторі зв'язок між амплітудами струму Im і напруги Um є аналогічний такому для постійного струму:
|
|
${{I}_{m}}=\frac{{{U}_{m}}}{{{X}_{c}}}$, |
(2.24) |
Але, як видно з рівнянь (2.22) і (2.17), для миттєвих значень
$i\ne \frac{u}{{{X}_{c}}}$,
тобто,
| для миттєвих значень струму і напруги на конденсаторі закон Ома не виконується. |
 У колі змінного струму котушка теж створює специфічний індутривний опір, за який є відповідальним явище самоіндукції ([ІІІ], п. 1.4) Якщо котушку з індуктивністю L і активним опором R підключити до генератора змінної напруги (рис.14.6а), то струм i в ній буде визначатися не тільки напругою генератора \(u=U_{m}\sin\omega{t}\), а й ЕРС самоіндукції ${{\E}_{c}}=-L{i}'$, так що
У колі змінного струму котушка теж створює специфічний індутривний опір, за який є відповідальним явище самоіндукції ([ІІІ], п. 1.4) Якщо котушку з індуктивністю L і активним опором R підключити до генератора змінної напруги (рис.14.6а), то струм i в ній буде визначатися не тільки напругою генератора \(u=U_{m}\sin\omega{t}\), а й ЕРС самоіндукції ${{\E}_{c}}=-L{i}'$, так що
$iR={{U}_{m}}\sin \omega t-L{i}'$
Звідси для струму в ідеальній (R = 0) котушці (рис.14.6б) отримуємо наступне диференціальне рівняння
|
${i}'=\frac{{{U}_{m}}}{R}\sin \omega t$, |
(2.25) |
з якого випливає, що струм змінюється за законом
|
|
\(i=I_{m}\sin\left(\omega{t}-\frac{\pi}{2}\right)\), |
(2.26) |
де величина
|
\(I_{m}=\frac{U_{m}}{X_{L}}\) |
(2.27) |
є його амплітудою, а
|
|
\(X_{L}=\omega{L}=2\pi\nu{L}\) |
(2.28) |
— індуктивним опором котушки.
Отже, для котушки індуктивності зв'язок між амплітуди струму Im і напруги Um в котушці індуктивності є пов'язані між собою так, як і резисторі та конденсаторі. Але для миттєвих значень такого зв'язку немає:
\(i\ne{u}/X_{L}\).
Отже, як і в конденсаторі,
|
миттєві значення сили змінного струму і напруги в котушці індуктивності закон Ома не задовольняють. |
Зрозуміло, що розглянутий зв'язок між амплітудами є чинним і в нерозгалуженому (послідовному) колі, що містить всі три види опордв. Це відображає закон Ома для змінного струму:
|
амплітуда сили змінного струму в колі є прямо пропорційна амплітуді напруги (ЕРС) генератора і обернено пропорційна повному опору кола: |
|
|
\(I_{m}=\frac{U_{m}}{Z}\). |
(2.29) |
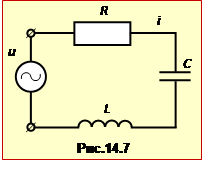 При цьому повний опір Z, інакше — "імпеданс", визначається параметрами елементів кола (R, L, C) і способом їхнього з'єднання. Для найпростішого послідовного кола (рис.14.7)
При цьому повний опір Z, інакше — "імпеданс", визначається параметрами елементів кола (R, L, C) і способом їхнього з'єднання. Для найпростішого послідовного кола (рис.14.7)
|
\(Z=\sqrt{R^{2}+(X_{L}-X_{C})^{2}}\), |
(2.30) |
або
|
\(Z=\sqrt{R^{2}+\left(\omega{L}-\frac{1}{\omega{C}}\right)^{2}}\). |
(2.31) |
Закон Ома для змінного струму стосується тільки амплітуд. Для миттєвих значень сили струму він не виконується, тобто сила струму в даний момент часу не дорівнює відношенню напруги в цей момент до повного опору. Але це не суперечить співвідношенню (2.29), тому що сила струму і напруга здійснюють коливання зі зсувом фаз і досягають своїх максимальних значень Im і Um не одночасно.
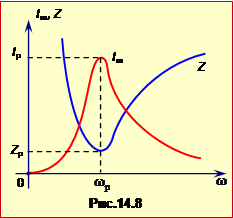 Згідно з виразом (2.31), Повний опір Z , тож і амплітуда сили струму, залежать від частоти, як показує рис.14.8. Він, зокрема, відображує явище резонансу в колі змунного струму, що полягає у різкому збільшенні амплітуди при наближенні коливань струму до резонансної частоти \(\omega_{р}\), яка відповідає мінімуму повного опору кола й знаходиться з умови
Згідно з виразом (2.31), Повний опір Z , тож і амплітуда сили струму, залежать від частоти, як показує рис.14.8. Він, зокрема, відображує явище резонансу в колі змунного струму, що полягає у різкому збільшенні амплітуди при наближенні коливань струму до резонансної частоти \(\omega_{р}\), яка відповідає мінімуму повного опору кола й знаходиться з умови
|
\(\omega_{р}L-\frac{1}{\omega_{р}C}\) = 0 \(\Rightarrow\) \(\omega_{р}=\frac{1}{\sqrt{LC}}\), |
(2.32) |
що збігається із власною частотою ідеального контутру з такими самою ємністю та індуктивністю (фомула 2.16).
При резонансі повний опір Zр і резонансна амплітуда струму Iр відповідно до формул (2.31) та (2.29), дорівнюють
\(Z_{0}=R\),
\(I_{р}=\frac{U_{m}}{R}\).
Видно, що при резонансі відбувається компенсація ємнісного й індуктивного опорів. Це пояснюється тим, що напруга на конденсаторі й котушці змінюються в протифазі, тож віднімаються.
Потужність змінного струму, що виділяється в колі у кожний момент часу, дорівнює добутку миттєвих значень сили струму і напруги. Ця миттєва потужність змінюється з великою частотою і її достатньо складно безпосередньо виміряти. Тому на практиці потужністю змінного струму називають середнє значення добутку сили струму й напруги.
Повна потужність у колі змінного струму виражається формулою
|
|
\(P=\frac{1}{2}I_{m}U_{m}\cos\varphi\), |
(2.33) |
де Im, Um – амплітуди сили струму і напруги генератора, \(\varphi\) – різниця фаз між коливаннями струму і напруги генератора.
Величина \(\cos\varphi\) називається коефіцієнтом потужності і виражається через активний і повний опір кола формулою
|
|
\(\cos\varphi=\frac{R}{Z}\). |
(2.34) |
Якщо підставити цей вираз у формулу (2.33) і врахувати закон Ома (формула (2.29), то виходить
|
|
\(P=\frac{I_{m}^{2}}{2}R=\frac{U_{Rm}^{2}}{2R}\), |
(2.35) |
де U = ImR – напруги на активному опорі кола.
Така ж потужність виділялася б у колі постійного струму з опором R при силі струму і напрузі
|
|
\(I=\frac{I_{m}}{\sqrt{2}}\), \(U=\frac{U_{m}}{\sqrt{2}}\). |
(2.36) |
Величини I та U, що визначаються формулами (2.36), називаються діючими, або ж ефективними значеннями сили струму і напруги.
Діючі значення є загальноприйнятими практичними характеристиками змінного струму. Зокрема, електровимірювальні прилади показують діючі значення, тож номінальні величини струмів і напруг на побутових приладах теж вказують у діючих значеннях.
Зважаючи на зв'язок між діючими значеннями та амплітудами, для діючих значень теж виконується закон Ома:
|
\(I=\frac{U}{Z}\). |
(2.37) |
застосуванням діючих значень струму й напруги формули потужності (2.33) і (2.35) записуються у вигляді
|
|
\(P=IU\cos\varphi\), |
(2.38) |
та
|
|
\(P=I^{2}R=\frac{U^{2}}{R}\). |
(2.39) |
Остання формула показує, що споживана від генератора потужність змінного струму, виділяється тільки на активному опорі, а реактивні елементи – конденсатор і котушка індуктивності – енергії не споживають. Це пов'язано з тим, що при зарядці конденсатор поглинає відповідну енергію, а при розрядці – повністю повертає її в коло. Те ж саме відбувається і у котушці індуктивності при збільшенні і зменшенні сили струму.
Одним із специфічних елементів кола змінного струму є трансформатор – пристрій для зміни ("трансформації") напруги від її значення на вході до потрібної величини на виході.
Найпростіший трансформатор складається з двох обмоток (намотаних ізольованим дротом котушок), які надіто на замкнене залізне осердя (рис. 14.9 ). Обмотка, на котру подається вхідна напруга, называється первинною, а інша – вторинною. Якщо напруга на вторинній обмотці ${{U}_{2}}$ більша, ніж на первинній ${{U}_{1}}$, трансформатор називають підвищувальним, інакше (при ${{U}_{2}}<{{U}_{1}}$) – знижувальним.
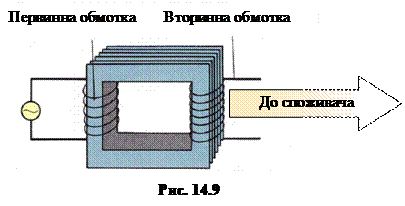
Роботу транcформатора, котра ґрунтується на явищі електромагнітної індукції ([3], п. 1.4), спрощено можна пояснити так. Унаслідок намагнічування осердя струмом первинної обмотки, через поперечний переріз обох обмоток створюється однаковий змінний магнітний потік і, згідно із законом Фарадея ([3], ф-ли (3.11), (3.13)), виникає однакова ЕРС індукції $\varepsilon$ в кожному витку. Тож при кількості витків ${{N}_{1}} і {{N}_{2}}$ у всій обмотці ЕРС індукції ${{\E}_{1}}={{N}_{1}}\varepsilon $ та ${{\E}_{2}}={{N}_{2}}\varepsilon $, відповідно. При цьому величина ${{\E}_{1}}$ задається вхідною напругою
|
${{\E}_{1}}={{U}_{1}}={{N}_{1}}\varepsilon $. |
|
Вторинна обмотка для навантаження (підключених пристроїв) відіграє роль джерела живлення. Тому в режимі "холостого ходу" (коли вторинну обмотку розімкнено) величина ${{\E}_{2}}$ збігається з напругою на клемах:
|
${{\E}_{2}}={{U}_{2}}={{N}_{2}}\varepsilon $ |
|
Таким чином, відношення вхідної та вихідної напруг, яке називається коефіцієнтом трансформації, дорівнює
|
|
$k=\frac{{{U}_{1}}}{{{U}_{2}}}=\frac{{{\E}_{1}}}{{{\E}_{2}}}=\frac{{{N}_{1}}}{{{N}_{2}}}.$ |
(2.40). |
Як видно, для знижувального трансформатора $k>1$, а для підвищувального $k<1$. Отже, величина k формально визначає не лише ступінь, а й напрям зміни напруги на виході трансформатора. Але на практиці вид трансформації визначають словесно. Приміром, говорять "підвищувальний трансформатор з коефіцієнтом трансформації 10", а не 0,1.
Наостанок зауважимо, що наведені викладки, строго говорячи, є наближеними, бо не враховують нявність у обмоток активного опору й витрати енергії струму на їхнє нагрівання та на перемагнічуваня осердя. Але, через порівняно малий активний опір обмоток та специфіку виготовленя осердь, ці втрати є неістотними, і ККД транформаторів є близький до одиниці.
_
Додаток. Розв'язок рівняння (2.25) можна отримати або прямим інтегруванням, або опосередковано, наступним чином. З математики відомо, що (coskx)′ = – k(sinkx), отже
$\sin \omega t=-\frac{1}{\omega }{{\left( \cos \omega t \right)}^{\prime }}$.
Підставивши цей вираз у рівняння (2.26), дістанемо
$L{i}'=\frac{{{U}_{m}}}{\omega }{{\left( \cos \omega t \right)}^{\prime }}$,
звідки випливає вираз
$i=\frac{{{U}_{m}}}{\omega L}\cos \omega t$,
що є рівнозначно виразу (2.26).