ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
2. Приклади розв’язування задач
2.2. Динаміка та енергія гармонічних коливань
У розглянутих далі задачах по замовчуванню вважається, що сили тертя та опору відсутні і g = 10 м/с2.
Задача 1.4. Визначити період T малих коливань кульки масою m = 40 г із зарядом $\left| q \right|$ = 8 мкКл, яку підвішено на тонкій шовковій нитці довжиною l = 1 м у напрямленому вертикально вгору електричному полі з напруженістю E = 300 В/см.
Задача 1.5. Пружну кульку на нитці довжиною l = 0,5 м прикріплено до пружної стінки, що нахилена під малим кутом \(\alpha\) до вертикалі, (див. розв'язок, рис. 4). Визначити, з яким інтервалом часу T кулька вдарятиме в стінку, якщо нитку відвести на кут θ0 = 2\(\alpha\) й відпустити.
Задача 1.6. Відкачаний до тиску P = 5 кПа горизонтальний циліндр поперечим перерізом S = 50 см2 поділено рухомим поршнем масою m = 2 кг на дві однакові частини довжиною l = 1 м кожна. Нехтуючи товщиною поршня, визначити період T коливань поршня внаслідок незначного поштовху.
Задача 1.7. Визначити період T та амплітуду A коливань пластини масою M = 1,5 кг на вертикальній пружині жорсткістю k = 250 Н/м після падіння на неї шматка пластиліну масою m = 0,5 кг з висоти h = 20 см.
Задача 1.8. Показати, що потенціальна енергія малих коливань математичного маятника масою m і довжиною l визначається формулою \(W_{п}=\frac{kx^{2}}{2}\), де \(k=\frac{mg}{l}\).
Задача 1.9. Визначити період T гармонічних коливань маятника на момент, коли потенціальна енергія коливань складає n = 80 % від повної, а зміщення з положення рівноваги та швидкість мають значення x = 2 см і v = 3,1 см/с.
Задача 1.4
Визначити
період T малих коливань кульки масою m = 40 г із зарядом $\left| q \right|$ = 8 мкКл, яку підвішено на тонкій шовковій нитці довжиною l = 1 м у напрямленому вертикально вгору електричному полі з напруженістю E = 300 В/см.
|
Дано:
m = 40 г = 0,04 кг
q = 8 мкКл = 8·10–6 Кл l = 1 м E = 300 В/cм = 3·104 В/м
|
| T-? |
Розв'язання
Кулька на нитці являє собою математичний маятник (п. 1.3), тож період її коливань задається загальним виразом (1.13) і формулою (1.18). Але за умовою на кульку, крім сили тяжіння $m\vec{g}$, діє ще й вертикальна електрична сила $q\vec{E}$, як показано на рис. 1.4 для випадку q > 0. Тому у виразі (1.16) замість mg має стояти \(\left| mg\mp \left| q \right|E \right|\). Тож
$k=\frac{\left| mg\mp \left| q \right|E \right|}{l}$,
де знак ''–'' відповідає випадку q > 0 і навпаки.
В такому разі період коливань кульки визначається виразом
|
$T=2\pi \sqrt{\frac{ml}{\left| mg\mp \left| q \right|E \right|}}$ |
Обчислення дають наступні значення:
q > 0 : T = 3,14 с; q < 0 : T = 1,57 с.
Задача 1.5.
Пружну кульку на нитці довжиною l = 0,5 м прикріплено до пружної стінки, що нахилена під малим кутом \(\alpha\) до вертикалі, рис 4.
Визначити,
з яким інтервалом часу T кулька вдарятиме в стінку, якщо нитку відвести на кут θ0 = 2\(\alpha\) й відпустити.
|
Дано: l = 0,5 м
|
|
T - ?
|
Розв’язання
Відповідно до умови кулька стикається зі стінкою пружньо, тобто без утрати енергії, й 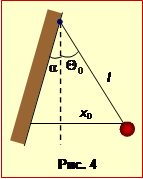 через рівні проміжки часу T, а в проміжках рухається, як математичний маятник за загальним рівнянням (1.4). Отже, якщо початкову координату кульки (відхилення від вертикалі) позначити як x0, то далі вона змінюється за законом
через рівні проміжки часу T, а в проміжках рухається, як математичний маятник за загальним рівнянням (1.4). Отже, якщо початкову координату кульки (відхилення від вертикалі) позначити як x0, то далі вона змінюється за законом
|
$x\left(t\right)={{x}_{0}}\cos {{\omega }}t$. |
(1) |
З урахуванням співвідношення між кутами \(\alpha\) і \(\Theta_{0}\), координата кульки на момент зіткнення зі стінкою t1 дорівнює x1 = –0,5x0, тож із рівняння (1) маємо:
$\cos \omega {{t}_{1}}=-0,5\quad \Rightarrow \quad \omega {{t}_{1}}=\frac{2\pi }{3}$
Відтак, узявши до уваги формулу (1.17) і те, що інтервал часу між послідовними зіткненнями кульки зі стінкою T = 2t1, отримаємо наступну відповідь задачі:
$T=\frac{4\pi }{3}\sqrt{\frac{l}{g}}$ = 0,95 с
Задача 1.6
Відкачаний до тиску P = 5 кПа горизонтальний циліндр перерізом S = 50 см2 поділено рухомим поршнем масою m = 1 кг на дві частини довжиною l = 1 м кожна. Нехтуючи товщиною поршня,
визначити
період T коливань поршня внаслідок незначного поштовху.
Дано:
|
l = 1 м
m = 2 кг
S = 50 см2 = 5·10–3 м2
P = 5 кПа = 5·103 Па
|
|
T - ? |
Розв’язання
При відведенні поршня з рівноважного положення в будь-який бік компенсація сил тиску повітря ${{\vec{F}}_{1}}$, ${{\vec{F}}_{2}}$ (рис. 6 ) порушується так, що їхня рівнодійна $\vec{F}$ є спрямована протилежно й має проєкцію на вісь ОХ
|
Fx = (Р1 – Р2)S. |
(1) |
Тому після вивільнення поршень починає коливатися з періодом, який визначається залежністю Fx(х) повертаючої сили від зміщення x поршня з положення рівноваги. Ця залежнічсть на загал може бути складною, але в даній задачі ситуація спрощується тим, що при малих коливаннях поршня температура повітря в циліндрі лишається сталою. Тож зміна його тиску та об'єму відбувається ізотермічно і є підпорядкована закону Бойля-Маріотта ([ІІІ], п. 1.3) Отже, P1V1 = P2, V2 = PV і, врахувавши, що V1 = (l + x)S, V2 = (l – x)S і V = l S, маємо:
\(Pl=P_{1}(l-x)\) \(\Rightarrow\) \(P_{1}=\frac{Pl}{l-x}\);
\(Pl=P_{2}(l+x)\) \(\Rightarrow\) \(P_{2}=\frac{Pl}{l+x}\).
У такому разі
\(F_{x}=PlS\left(\frac{1}{l+x}-\frac{1}{l-x}\right)=-PlS\frac{2x}{l^{2}-x^{2}}\).
За умовою \(x\ll{l}\), тож величиною \(x^{2}\) у цьому виразі можна знехтувати, тож
|
|
\(F_{x}=-kx\), |
|
де
|
|
\(k=\frac{2PS}{l}\). |
|
Отриманий вираз \(F_{x}\) збігається з формулою (1.10). Отже, малі, коливання поршня є гармонічними, тож шуканий період T, згідно із загальною формулою (1.13), дорівнює
$T=2\pi \sqrt{\frac{ml}{2PS}}$ ≈ 1,3 c.
Задача 1.7
Визначити
період T та амплітуду A коливань пластини масою M = 1,5 кг на вертикальній пружині жорсткістю k = 250 Н/м після падіння на неї шматка пластиліну масою m = 0,5 кг з висоти h = 20 см (рис. 7).
|
Дано: k = 250 Н/м
M = 1,5 кг
h = 20 см = 0,2 м
m = 0,5 кг
|
|
T - ? A - ?
|
Розв’язання
Після падіння пластиліну на пластину створюється пружинний маятник (п. 1.3) масою (M + m) і жорсткістю k. Отже, шуканий період коливань T за формулою (1.15) дорівнює
| \(T=2\pi\sqrt{\frac{m+M}{k}}=\) 0,57 c. | (1) |
Спосіб 1. При зіткненні в точці О з координатою x = 0 пластилін пердає пластині деякий імпульс, через що її наступні коливання відбуваються з відповідною швидкістю v0 й
Коливання пластини з пластиліном відбуваються навколо точки O1, на відстані х0 від початкового положення, що визначається умовою компенсації сумарної ваги тіл і сили, з якою на них діє пружина:
| $ \left( M+m \right)g=k{{x}_{0}} $ $\Rightarrow $ ${{x}_{0}}=\frac{\left( M+m \right)g}{k}$ |
(2) |
При цьому коливання відбуваються не зі стану спокою, як зазвичай, а з певною початковою швидкістю v0, що визначається законом збереження імпульсу. Тож, зважаючи на непружний характер зіткнення
$mv=\left( M+m \right){{v}_{0}}$,
де v – швидкість пластиліну на момент падіння на пластину, котра складає (див. [І], ф-ла (1.19а)), $v=\sqrt{2gh}$ . Отже, початкова швидкість коливань пластини з пластиліном
| ${{v}_{0}}=\frac{m}{M+m}\sqrt{2gh}$. | (3) |
Рис. 7
Відтак при знайдених початкових умовах (x0, v0), із загальних рівняннь гармонічних коливань (1.4) і (1.5) виходить:
| $x=A\sin \left( \omega t+{{\varphi }_{0}} \right)$ $\Rightarrow $ $\frac{x}{A}=\sin \left( \omega t+{{\varphi }_{0}} \right)$ |
| ${{v}_{x}}=A\omega \cos \left( \omega t+{{\varphi }_{0}} \right)$ $\Rightarrow $ $\frac{{{v}_{x}}}{A\omega }=\cos \left( \omega t+{{\varphi }_{0}} \right)$, |
звідки, враховуючи відому тригонометричну тотожність, отримуємо:
\(\frac{x^{2}}{A^{2}}+\frac{v^{2}}{A^{2}\omega^{2}}=1\) \(\Rightarrow\) \(A=\sqrt{x^{2}+\frac{v^{2}}{\omega^{2}}}\).
Ця рівність виконцється при будь-якому положенні коливного тіла, тож поклавши x = x0, отримаємо :
$A=\sqrt{x_{0}^{2}+\frac{v_{0}^{2}}{{{\omega }^{2}}}}$ = $\sqrt{x_{0}^{2}+\frac{{{\left( {{v}_{0}}T \right)}^{2}}}{4{{\pi }^{2}}}}$
Відтак, узявши отримане напочатку (вираз (1)) значення T та обрахувавши за виразами (2) і (3) значення x0 і v0 , дістанемо:
А = 9,2 см.
Спосіб 2. Амплітуду коливань можна знайти, й спираючися не на співвідношеня механіки коливань. А саме.
Стискання пружини відбувається за рахунок енергії пластини з пластиліном . Тому, якщо прийняти потенціальну енрегію тіл у найнижчій точці за 0, то на момент зупинки вся їхня енергія перейде в енергію деформації пружини на величину відстані x від початкового до крайнього положення пластини. Отже,
$\frac{k{{x}^{2}}}{2}$ = $\frac{\left( M+m \right)v_{0}^{2}}{2}+\left( M+m \right)gx$ \(\Rightarrow\) $k{{x}^{2}}-2\left( M+m \right)gx-\left( M+m \right)v_{0}^{2}=0$
Корені цього рівняння складають:
${{x}_{1,2}}=\frac{\left( M+m \right)g}{k}\pm \sqrt{{{\left( \frac{\left( M+m \right)g}{k} \right)}^{2}}+\frac{\left( M+m \right)v_{0}^{2}}{k}}$
або, враховуючи вирази (2) і (3),
${{x}_{1,2}}={{x}_{0}}\pm \sqrt{{{\left( \frac{\left( M+m \right)g}{k} \right)}^{2}}+\frac{\left( M+m \right)2gh}{k}}$.
Зрозуміло, що другі доданки в цьому виразі визначають макимальне відхилення пластини з пластиліном від точки рівноваги сил, тобто шукану амплітуду коливань. Отже,
${A}=\sqrt{{{\left( \frac{\left( M+m \right)g}{k} \right)}^{2}}+\frac{\left( M+m \right)2gh}{k}}$.
Обчислення дають
A = 9,2 см,
що, природньо, збігається із отриманим раніше значенням. Варто також відмітити, що перший доданок під радикалом дорівнює $x_{0}^{2}$. Отже, пластина з пластиліном, незалежно від їхньої маси та жорсткості пружини, повертаючись із найнижчої точки, підніметься вище початкового положення. Це пояснюється тим, що коливання почалися не зі стану спокою, як зазвичай, і з певною початковою кінетичною енергією.
Задача 1.8
Показати,
що потенціальна енергія малих коливань математичного маятника масою m і довжиною l визначається формулою \(W_{п}=\frac{kx^{2}}{2}\), де \(k=\frac{mg}{l}\).
Розв’язання
Потенціальна енергія маятника обумовлена дією на нього сили тяжіння і виражається формулою
|
|
\(W_{п}=mgh\), |
(1) |
де m – маса маятника, h – висота підйому над положенням рівноваги (див. рис.8). З рис.8 видно, що
|
|
\(h=AO-AB=l-l\cos\alpha\) \(\Rightarrow\) \(h=l(1-\cos\alpha)=2l\sin^{2}\frac{\alpha}{2}\). |
(2) |
Оскільки маятник здійснює малі коливання (\(x\ll{l}\)), то \(\alpha\ll{1}\) рад. Тому \(\sin\frac{\alpha}{2}=\frac{\alpha}{2}\), і вираз (2) набуває вигляду:
\(h=2l\left(\frac{\alpha}{2}\right)^{2}=\frac{l\alpha^{2}}{2}\).
Підставивши його у формулу (1) і зробивши заміну \(\alpha=x/l\), отримаємо
\(W_{п}=\frac{mgx^{2}}{2l}=\frac{kx^{2}}{2}\),
де \(k=\frac{mg}{l}\), що і треба було довести.
Ця задача ілюструє універсальність формули (13.19): вона може бути застосовна до будь-яких гармонічних коливань, а не тільки до коливань під дією сили пружності.
Задача 1.9
Визначити
період T гармонічних коливань маятника на момент, коли потенціальна енергія коливань складає n = 80 % від повної, а зміщення з положення рівноваги та швидкість мають значення x = 2 см і v = 3,1 см/с.
|
Дано: n = 80 %
x = 2 см
v = 3,1 см/с
|
|
T - ? |
Розв’язання
Період коливань тіла на пружині визначається формулою:
|
|
\(T=2\pi\sqrt{\frac{m}{k}}\). |
(1) |
Відношення (m/k) знайдемо через повну енергію коливань:
|
|
\(W=\frac{mv^{2}}{2}+\frac{kx^{2}}{2}=W_{п}\left(\frac{mv^{2}}{kx^{2}}+1\right)\), |
(2) |
де (\(mv^{2}/2\)) – кінетична і (\(kx^{2}/2\)) – потенціальна енергія. Відтак із виразу (2) одержимо
\(\frac{m}{k}=\frac{x^{2}}{v^{2}}\left(\frac{W}{W_{п}}-1\right)\).
і після підстановку у формулу (1) дістанемо відповідь:
\(T=2\pi\frac{x}{v}\sqrt{\frac{W}{W_{п}}-1}=2\pi\cdot\frac{2}{3,1}\sqrt{\frac{1}{0,8}-1}\approx\) 2 c.