ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
1.Теоретичні відомості.
1.2. Швидкість, прискорення і сила при гармонічних коливаннях
Рівняння швидкості точки при гармонічних коливаннях одержимо, взявши першу похідну по часу від координати (рівняння (1.4)):
|
|
\(v_{x}=x^{\prime}(t)=-\omega{x}_{m}\sin(\omega{t}+\varphi_{0})\), |
(1.5) |
або
|
|
\(v_{x}=v_{m}\cos\left(\omega{t}+\varphi_{0}+\frac{\pi}{2}\right)\), |
(1.5a) |
де vm – амплітуда швидкості, що пов'язана з амплітудою зміщення xm співвідношенням
|
|
\(v_{m}=\omega{x}_{m}\). |
(1.6) |
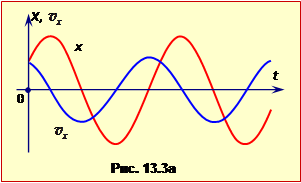
Порівнюючи рівняння (1.4) і (1.5), бачимо, що коливання швидкості за фазою випереджають коливання координати точки на \(\pi/2\) або на чверть періоду (рис.1.3а).
Рівняння прискорення одержимо, визначивши похідну швидкості з рівняння (1.5):
|
|
\(a_{x}=v_{x}^{\prime}=-\omega^{2}x_{m}\cos(\omega{t}+\varphi_{0})\) |
|
або
|
|
\(a_{x}=a_{m}\cos(\omega{t}+\varphi_{0}+\pi)\), |
(1.7) |
де величина
|
\(a_{m}=\omega^{2}x_{m}\), |
(1.8) |
|||
є амплітудою прискорення, котру, згідно з виразом (1.6), можна подати й так:
|
\(a_{m}=\omega{v}_{m}\). |
(1.8а) |
|||
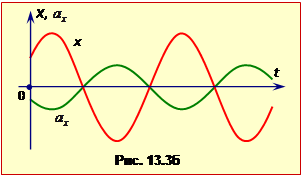
З рівняння (1.7) видно, що коливання прискорення відбуваються з різницею фаз \(\pi\), тобто в протифазі до коливань координати (рис.1.3б).
Слід зауважити, що тригонометрична функція в рівняннях швидкості й прискорення є визначена неоднозначно і залежить від вигляду цієї функції в рівнянні зміщення. До прикладу, при використанні рівняння (1.1a) у рівнянні (1.5) буде фігурувати функція \(\cos\), а в рівнянні (1.6) – функція \(\sin\). Але будь-що,
|
|
\(a_{x}=-\omega^{2}{x}\), |
(1.9) |
тобто,
|
при гармонічних коливаннях прискорення точки в будь-який момент є прямо пропорційне до її зміщення з положення рівноваги й напрямлене до нього. |
Відповідно до другого закону Ньютона та рівняння (1.9), прикладена до коливної точки рівнодійна сила у будь-який момент часу визначається, як
|
|
\(F_{x}=-kx\), |
(1.10) |
де
|
|
\(k=m\omega^{2}\). |
(1.11) |
Формула виражає критерій гармонічності механічних коливань:
|
якщо рівнодійна сил, які діють на матеріальну точку, є прямо пропорційною до зміщення з положення рівноваги й і спрямована до нього, то точка здійснює гармонічні коливання. |
При цьому частота і період гармонічних коливань визначаються наступними загальними формулами:
|
|
\(\omega=\sqrt{\frac{k}{m}}\). |
(1.12) |
||
|
|
\(\nu=\frac{1}{2\pi}\sqrt{\frac{k}{m}}\). |
(1.12а) |
||
|
|
\(T=2\pi\sqrt{\frac{m}{k}}\), |
(1.13) |
||
де m – маса матеріальної точки, що коливається, k – коефіцієнт пропорційності між рівнодійною силою і відхиленням точки від положення рівноваги.