ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
1.Теоретичні відомості.
1.3. Маятники.
Маятниками називають тіла, здатні здійснювати вільні коливання навколо фіксованого положення рівноваги. Найпростішими серед них є пружинний та математичний маятники.
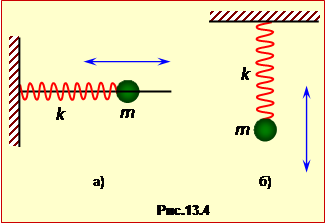
Пружинний маятник являє собою тіло маси m, з'єднане з невагомою пружиною жорсткістю k із закріпленим іншим кінцем (рис.1.4).
За відсутності сил тертя та опору повітря (на практиці – коли ними можна нехтувати), рух маятника визначається тільки силою пружності ([І], розділ V) у деформованій пружині, котра задовольняє умову (1.10)
\(F=-kx\),
де x – величина деформації.
Отже,
пружинний маятник здійснює гармонічні коливання з циклічною частотою
|
|
\(\omega=\sqrt{\frac{k}{m}}\) |
(1.14) |
і періодом
|
|
\(T=2\pi\sqrt{\frac{m}{k}}\), |
(1.15) |
де m – маса маятника, k – жорсткість пружини.
Все сказане стосується як горизонтальних (рис.1.4а), так і вертикальних (рис.1.4б) коливань, але в останньому випадку величина x не включає статичну деформацюю пружини маятника під дією сили тяжіння.
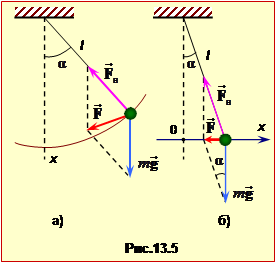 Математичний маятник являє собою тіло маси m на невагомому нерозтяжному підвісі довжиною l із закріпленим кінцем (рис. 1.5).
Математичний маятник являє собою тіло маси m на невагомому нерозтяжному підвісі довжиною l із закріпленим кінцем (рис. 1.5).
За відсутності сил тертя в підвісі та опору середовища рух маятника відбувається під дією сил тяжіння \(m\vec{g}\) і натягу підвісу \(\vec{F}_{н}\), рівнодійна яких
\(\vec{F}=m\vec{g}+\vec{F}_{н}\)
при значних відхиленнях маятника (рис.1.5а) складно залежить від кута \(\alpha\). Тому довільні коливання математичного маятника не є гармонічними. Одначе при малих амплітудах ситуація спрощується, бо при \(\alpha\ll{1}\) \(\mathrm{tg}\alpha=\sin\alpha=\alpha\). Отже, можна вважати, що малі коливання математичного маятника відбуваються вздовж горизонтальної осі ОХ (рис.1.5б) під дією повертаючої сили
\(F_{x}=-mg\cdot\mathrm{tg}\alpha=-mg\alpha\).
З тієї ж причини можна прийняти, що в будь-який момент часу кут відхилення маятника від положення рівноваги α = (x/l). У такому разі
\(F_{x}=-kx\),
де x – зміщення маятника з положення рівноваги і
|
|
\(k=\frac{mg}{l}\), |
(1.16) |
Отже, згідно з критерієм (1.10),
|
малі вільні коливання математичного маятника є гармонічними. |
Зіставивши вираз (1.16) з формулами (1.12) та (1.13), дісттанемо наступні формули для циклічної частоти \(\omega\) та періоду T коливань математичного маятника:
|
|
\(\omega=\sqrt{\frac{g}{l}}\); |
(1.17) |
|
|
\(T=2\pi\sqrt{\frac{l}{g}}\). |
(1.18) |