ФІЗИКА. Вчимося розв'язувати задачі. "ЕЛЕКТРИКА І МАГНЕТИЗМ". Компенсаційний курс
Розділ ІІІ. Магнітне поле та електромагнітна індукція
Рух заряджених частинок у магнітному полі
≈
|
Особливістю задач даної теми є те, що рух зарядів в магнітному полі є рівномірний і, за винятком руху вздовж напрямку поля, криволінійний. За наявності ще й електричного поля слід розглянути віртуальний рух частинки в кожному з полів окремо, а потім "синтезувати" реальний рух. |
У наведених далі задачах по умовчанню поля приймаються за однорідні, й при розрахунках g = 10 м/с2.
Задача 3.5. Авіалайнер із розмахом крил l = 20 м горизонтально пролітає над полюсом зі швидкістю v = 900 км/год. Прийнявши, що магнітне поле Землі в зоні польоту є вертикальним і має індукцію B = 60 мкТл, визначити: а) різницю потенціалів U на кінцях крил; б) покази підключеного до них міліамперметра I із внутрішнім опором R = 0,5 Ом.
Задача 3.6. Електрон влітає в смугу взаємно перпендикулярних електричного (E = 10 кВ/м) та магнітного (B = 10 мТл) полів. Визначити найменшу величину та напрямок швидкості електрона, при яких поля не впливатимуть на його подальший рух.
Задача 3.7. На гладку горизонтальну поверхню, що знаходиться в горизонтальних взаємно перпендикулярних електричному Е = 10 В/см й магнітному В = 20 мТл полях, кладуть і без поштовху відпускають кульку з масою m = 10 мг і зарядом q = 50 мкКл. Відтак кулька через деякий час відривається від поверхні. Визначити, яку відстань S проходить кулька до відриву.
Задача 3.8. Протон, який пройшов прискорювальну напругу U = 100 В, по нормалі входить і наскрізь пролітає плоску смугу паралельного до її поверхонь магнітного поля з індукцією B = 5 мТл. Визначити, на якій відстані S від точки входження та під яким кутом φ протон вийде зі смуги, якщо її товщина d = 25 см .
Задача 3.9. У вільному просторі, в якому зі швидкістю v = 0,5 Мм/с рухається протон (питомий заряд qп = (e/m) дорівнює 9,58·107 Кл/кг), "вмикають" перпендикулярні до його руху та однаково спрямовані електричне (E = 2 кВ/м) і магнітне (B = 10 мТл) поля. Визначити: А) прискорення протона; Б) параметри траєкторії його подальшого руху .
Задача 3.10. Прискорений напругою U = 400 В протон (питомий заряд qп = (e/m) дорівнює 9,58·107 Кл/кг) по нормалі влітає в зону паралельних електричного (Е = 20 В/cм) та магнітного (В = 20 мТл) полів із паралельною до них плоскою межею. Визначити відстань L від точки входження та швидкість v і кут виходу $\vartheta$ протона з полів.
Задача 3.11. Металевий стрижень довжиною l = 25 см, що знаходиться в магнітному полі В = 100 мТл, обертається навколо одного кінця з кутовою швидкістю ω = 2 рад/с в перпендикулярній до напряму поля площині. Визначити напругу U (різницю потенціалів) на кінцях стрижня.
Задача 3.5. Авіалайнер із розмахом крил d = 20 м горизонтально пролітає над полюсом зі швидкістю v = 900 км/год. Прийнявши, що магнітне поле Землі в зоні польоту є вертикальним і має індукцію B = 60 мкТл,
визначити:
а) різницю потенціалів U на кінцях крил;
б) покази підключеного до них міліамперметра I із внутрішнім опором R = 0,5 Ом.
|
Дано: d = 20 м v = 900 км/год B = 60 мкТл R = 0,5 Ом |
|
U - ? I - ? |
Розв'язання
а). При горизонтальному польоті у вертикальному магнітному полі Землі біля полюсу на вільні електрони діє магнітна сила (формула 3.3а), котра створює рівні за величиною й протилежні за знаком надлишкові (''індуковані'') заряди на кінцях крил і відповідне електричне поле ${{\vec{E}}}$ всередині, як схематично показано на рисунку. Це поле нівелює дію магнітного поля ${{\vec{B}}}$, отже, відповідно до формул (1.2) і (3.1а), електрична сила, що діє на електрон, у кожній точці зрівноважує магнітну: 
|
${{\vec{F}}_{е}}$= – ${{\vec{F}}_{m}}$ $\Rightarrow $ $E=vB$. |
|
За умовою магнітне Землі є однорідним, а швидкість літака – сталою. В такому разі величина E в усіх точках однакова й не змінюється з часом. Отже, шукана різниця потенціалів (напруга) на кінцях крил задовольняє умову (1.20) і складає
| $U=vBd$ = 30 мВ. |
|
б). Це завдання є тривіальним. Справді, в крилах і підключених до них провідниках із міліамперметром на електрони діють однакові за напрямом і величиною магнітні сили, що унеможливлює в утвореному замкненому контурі циркуляцію заряду, себто — електричний струм. Отже,
| I = 0. |
|
Задача 3.6. Електрон влітає в смугу взаємно перпендикулярних електричного (E = 10 кВ/м) та магнітного (B = 10 мТл) полів.
Визначити,
найменшу величину та напрямок швидкості електрона, при яких поля не впливатимуть на його подальший рух.
|
Дано: E = 10 кВ/м B = 10 мТл |
|
\(\vec{v}\) - ? |
Розв'язання
Задля зручності зв'яжемо з електроном систему координат XOZ, в якій поля \(\vec{B}\) і \(\vec{E}\) спрямован0, як на рис. 6.
Аби електрон рухався з незмінною за величиною й напрямом швидкістю \(\vec{v}\), сили, що діють на нього з боку електричного та магнітного полів мають бути компенсовані:
|
\(\vec{F}_{е}\) = –\(\vec{F}_{м}\) \(\Rightarrow\) \({F}_{е}\) = \({F}_{м}\). |
(1) |
Тож, відповідно до правила правого гвинта, що визначає напрям магнітної сили, вектор швидкості електрона \(\vec{v}\) має лежати в площині XOZ і в загальному випадку складати якийсь кут α з вектором \(\vec{B}\). Тож для необхідної швидкості електрона за формулами (1.2) і (3.3) маємо:
\(eE=evB\sin\alpha\) \(\Rightarrow\) \(v=\frac{E}{B\sin\alpha}\).
Звідси очевидно, що величина v, як вимагає умова, буде мінімальною, коли електрон влетить перпендикулярно до площини полів із швидкістю
\(v=\frac{E}{B}\) = 106 м/с.
Задача 3.7. На гладку горизонтальну поверхню, що знаходиться в горизонтальних і взаємно перпендикулярних електричному (Е = 5 В/см) та магнітному (В = 20 мТл) полях, кладуть і без поштовху відпускають кульку масою m = 10 мг і зарядом q = 50 мкКл. Відтак кулька через деякий час відривається від поверхні.
Визначити,
яку відстань S проходить кулька до відриву.
|
Дано: Е = 5 В/см В = 20 мТл m = 10 мг q = 50 мкКл |
|
S - ? |
Розв'язання

На кульку після вивільнення, крім сили тяжіння $m\vec{g}$ та електричної ${{\vec{F}}_{e}}$ діє ще й магнітна сила ${{\vec{F}}_{m}}$. Ця сила при показаній на рис. 7 взаємній орієнтації полів за правилом правого гвинта (п. 1.1) є спрямована вертикально вгору і при певній швидкості кульки може спричинити її відрив від опори. Відповідно до формули (3.1), це може статися, коли
| $v=\frac{mg}{qB}$. |
(1) |
Рух кульки відбувається під дією однорідного електричного поля і є рівноприскореним. Отже, необхідної для відриву швидкості кулька набуде на відстані S, яка задовольняє відоме співвідношення механіки ( [І], ф-ла (1.19))
| $S=\frac{{{v}^{2}}}{2a}$ |
(2) |
і, враховуючи вираз (1),
| $S=\frac{{{m}^{2}}{{g}^{2}}}{2{{q}^{2}}{{B}^{2}}a}$ |
(3) |
де a – прискорення кульки, котре створюється електричною силою Fe = qE і за другим законом Ньютона дорівнює
| $a=\frac{qE}{m}$ |
|
Отже, відстань, на якій кулька відірветься від поверхні, дорівнює
| $S=\frac{{{m}^{3}}{{g}^{2}}}{2{{q}^{3}}{{B}^{2}}E}$. |
|
Обчислення дають
| S = 2 м. |
|
Задача 3.8. Протон, який пройшов прискорювальну напругу U = 100 В, по нормалі входить і наскрізь пролітає плоску смугу паралельного до її поверхонь магнітного поля з індукцією B = 5 мТл.
Визначити,
на якій відстані S від точки входження та під яким кутом φ протон вийде зі смуги, якщо її товщина d = 25 см.
|
Дано: U = 100 В B = 5 мТл = 5·10-3 Тл d = 25 см = 0,25 м |
|
S - ? φ - ? |
Розв'язання

Позаяк протон влітає в смугу перпендикулярно до її поверхні, тож і напрямку магнітного поля, далі він рухається по дузі кола певного радіуса R (див. п. 1.2) з центром О на передній стінці смуги, як показано на рис. 8. Отже, шукана відстань S дорівнює довжині основи АС рівнобічного трикутника ОАС з бічною стороною R, а кут виходу φ збігається із кутом при вершині цього трикутника, позаяк його сторони є перпендикулярні до векторів ${{\vec{v}}_{0}}$ і ${{\vec{v}}}$. При цьому величину R можна знайти за формулою (3.4) через задану індукцію магнітного поля В, відомий питомий заряд протона qп та швидкість його входження в смугу v, котра залежить від прискорювальної напруги U. Через це відповіді задачі можна знайти з наступних співвідношень між показаними на рис. 8 характеристиками траєкторії протона:
|
$\frac{d}{S}=\cos \frac{\varphi }{2}$; |
(1) |
|
$\frac{S}{2R}=\sin \frac{\varphi }{2}$. |
(2) |
А саме, піднісши до квадрата та почленно додавши записані рівності, отримаємо біквадратне рівняння
| ${{\left( \frac{d}{S} \right)}^{2}}+{{\left( \frac{S}{2R} \right)}^{2}}=1\quad \Rightarrow \quad {{S}^{4}}-4{{R}^{2}}{{S}^{2}}+4{{R}^{2}}{{d}^{2}}=0$ |
(3) |
одним із коренів якого є шукана величина S. Аби виокремити цей корінь, візьмемо до уваги, що радіус траєкторії протона має задовольняти умову R ≥ d, а відстань S ≤ $\sqrt{2}R$, інакше протон не подолає смугу поля. В такому разі
| S = R$\sqrt{2\left( 1-\sqrt{1-{{\left( {d}/{R}\; \right)}^{2}}} \right)}$. |
(4) |
Отже, аби знайти відстань між точками входу та виходу протона зі смуги, треба спершу обчислити радіус його траєкторії R формула (3.4). Потрібну для цього швидкість протона v знайдемо через його кінетичну енергію, що дорівнює роботі прискорювального електричного поля (формула 1.13):
$\frac{mv_{0}^{2}}{2}=eU$ \(\Rightarrow\) ${{v}_{0}}=\sqrt{2{{q}_{п}}U}$
і, врахувавши формулу (3.4) та значення qп = 9,58·107 Кл/кг , отримаємо
| $R=\frac{1}{B}\sqrt{\frac{2U}{{{q}_{п}}}}$ = 29 см. |
|
Підставивши цу значення у вираз (4), знайдемо наступну величину відстані між точками входу та виходу протона із смуги магнітного поля:
S = 28,5 см,
Відтак із з виразу (1) знайдемо і кут вильоту протона зі смуги:
$\varphi =2\cdot \arccos \frac{d}{S}$ ≈ 57°.
Задача 3.9.
У вільному просторі, в якому зі швидкістю v = 0,5 Мм/с рухається протон (питомий заряд qп = (e/m) = 9,58·107 Кл/кг), "вмикають" перпендикулярні до його руху та однаково спрямовані електричне (E = 2 кВ/м) і магнітне (B = 10 мТл) поля.
Визначити:
А) прискорення протона;
Б) параметри траєкторії його подальшого руху.
|
Дано: v = 0,5 Мм/с = 5·105 м/с E = 2 кВ/м = 2·103 В/м
B = 10 мТл = 10-2 Тл
q/m = 9,58·107 Кл/кг
|
|
a - ?
R - ? h - ?
|
Розв'язання
При ввімкненні полів на протон почнуть діяти взаємно перпендикулярні магнітна \(\vec{F}_{м}\) і електрична \(\vec{F}_{е}\) сили (рис.9). Тож протон буде рівномірно рухатися по колу в перпендикулярній до напрямку полів площині під дією магнітної сили (див. п. 1.2) й одночасно прискорено рухатись уздовж полів під дією електричної сили (розділ І, п. 1.1). При цьому електрична сила не буде впливати на обертальну, а магнітна – на поступальну складову руху протона. Як наслідок, він буде рухатись уздовж полів по гвинтовій лінії з постійним радіусом кривини й змінним кроком, як схематично показано на рис. 9-1.
А). Згідно зі сказаним, прискорення протона \(\vec{a}\) складається з двох незалежних компонент електричної (\(\vec{a}_{1})\) і магнітної \(\vec{a}_{2}\), тож
\(\vec{a}\) = \(\vec{a}_{1}\) + \(\vec{a}_{2}\) $\Rightarrow $ $a=\sqrt{a_{1}^{2}+a_{2}^{2}}$,
де за другим законом Ньютона та формулами (1.2) і (3.3а)
|
${{a}_{1}}={{q}_{п}}E,\quad {{a}_{2}}={{q}_{п}}vB$. |
(1) |
Отже, шукане прискорення протона
$a={{q}_{п}}\sqrt{{{E}^{2}}+{{\left( vB \right)}^{2}}}\approx 5,2\cdot {{10}^{11}}$ м/с2.
 Б). Радіус витка гвинтової лінії, по якій рухається протон, визначається формулою (3.4):
Б). Радіус витка гвинтової лінії, по якій рухається протон, визначається формулою (3.4):
$R=\frac{v}{{{q}_{п}}B}$ = 52 см.
Кроком h гвинтової лінії називається зазор між витками, який звичайно дорівнює відстані між точками дотику сусідніх витків із будь-якої паралельною до осі гвинта прямою, приміром, віссю OZ (рис. 6-1). Але в даній задачі через дію на протон електричного поля крок буде змінюється від витка до витка й залежатиме від положення вказаної дотичної лінії. Тож будемо відміряти його від початкового положення протона. В такому разі для n-го витка крок hn дорівнює різниці відстаней, які протон проходить у напрямку електричного поля за проміжки часу tn = nT і tn-1 = (n–1)T, де T – період обертання протона по трєкторії. Тож згідно з відомою формулою кінематики ([І], ф-ла (1.17)) отримуємо:
${{h}_{n}}=\frac{{{a}_{1}}{{T}^{2}}}{2}\left( {{n}^{2}}-{{\left( n-1 \right)}^{2}} \right)$
або
${{h}_{n}}={{h}_{1}}\left( 2n-1 \right)$,
де
${{h}_{1}}=\frac{{{a}_{1}}{{T}^{2}}}{2}$
– початковий крок, який з урахуванням виразу (1) і формули (3.5а) дорівнює
| ${{h}_{1}}=\frac{2{{\pi }^{2}}E}{{{q}_{п}}{{B}^{2}}}$ = 8 м. |
(2) |
Прискорений напругою U = 400 В протон (питомий заряд (відношення заряду до маси) qп = 9,58·107 Кл/кг) по нормалі влітає в зону паралельних електричного (Е = 20 В/cм) та магнітного (В = 20 мТл) полів із паралельною до них плоскою межею.
Визначити,
відстань L від точки входження та швидкість v і кут виходу $\vartheta$ протона з полів.
|
Дано: Е = 20 В/cм В = 20 мТл U = 400 В qп= 9,58·107 Кл/кг |
|
L- ?, v-?, $\vartheta$-? |
Розв'язання
Оберемо систему координат з початком О в точці входження протона в поля і віссю ОХ, що за напрямом збігається з початковою швидкістю протона $\vec{v}_{0}$, як показано на рис. 10.
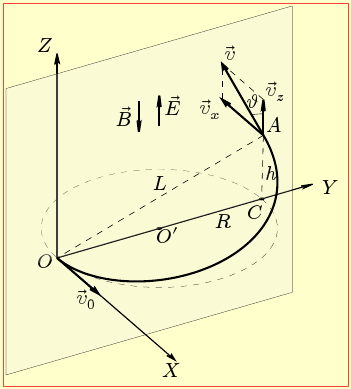
При такому виборі координатної системи умови руху протона при входженні польовій зоні є такі самі, як у Задачі 3.9, тож він почне рухатися навколо напрямку полів по гвинтовій лінії зі змінним кроком. Але через наявність межі (площина YOZ), протон перебуватиме в полях тільки протягом часу t у пів періоду обертання (3.5) навколо напряму полів:
| $t=\frac{\pi }{{{q}_{п}}B}$ |
(1) |
і здійснить тільки половину першого витка траєкторії.
За вказаних умов у кожний момент часу протон під дією магнітного поля обертатиметься із сталою швидкістю v = v0 в паралельній до {XOY} площині по колу радіуса R й одночасно рухатиметься у напрямку осі ОZ під дією електричного поля. При цьому за час t протон зміститься на відстань 2R вздовж осі OY і h в напрямку OZ. Отже шукана відстань між точками входження і виходу складає
| $L=\sqrt{4{{R}^{2}}+{{h}^{2}}}$. |
(2) |
Величину R знайдемо за формулою (3.4), в якій індукцію поля B в умові задано прямо, а поперечну швидкість протона v0 – опосередковано через його початкову кінетичну енергію, що дорівнює роботі прискорювального поля (1.13а):
| $\frac{mv_{0}^{2}}{2}=eU\quad \Rightarrow \quad {{v}_{0}}=\sqrt{2{{q}_{п}}U}$. |
(3) |
Відтак, підставивши це значення у формулу (3.4), дістанемо:
| $R=\frac{1}{B}\sqrt{\frac{2U}{{{q}_{п}}}}$. |
(4) |
Величина h, згідно з формулою кінематикою ([I], ф-ла (1.17)) складає
| $h=\frac{a{{t}^{2}}}{2}$, |
(5) |
де прискорення a створюється електричним полем і за ІІ законом Ньютона та формулою (1.20) дорівнює
|
$a=\frac{eE}{m}={{q}_{п}}E$, |
(6) |
а час руху протона t = (T/2) визначається виразом (1).
Тож, згідно з виразом (5), вертикальне зміщення протона дорівнює
| $h=\frac{{{\pi }^{2}}E}{2{{q}_{п}}{{B}^{2}}}$. |
(7) |
Відтак, обчисливши за формулами (4) і (7) значення R і h, із виразу (2) знайдемо:
$L$ = 38,7 см.
Далі, обчисливши за формулами (6) і (1) вертикальну складову vz = at і врахувавши, що горизонтальна vх = v0, знайдемо швидкість
$v=\sqrt{v_{0}^{2}+v_{1}^{2}}$ = 4,2·105 м/с
та через якусь із тригонометричних функцій – кут виходу виходу протона з полів:
$\vartheta$ = 41,4°.
|
Задача 3.11.  Металевий стрижень ОА (рис.11-1) довжиною l = 25 см, що знаходиться в магнітному полі В = 100 мТл, обертається навколо одного кінця з кутовою швидкістю ω = 2 рад/с в перпендикулярній до напряму поля площині . Визначити напругу U (різницю потенціалів) на кінцях стрижня. |
||||||
Через дію магнітного поля на вільні електрони (розділ ІІІ, п. 1.2) на кінцях Електрична та магнітна сили є протилежно спрямовані й компенсовані. Тож відповідно до (формул (1.2) та (3.3а) в кожній точці стрижня встановлюється стаціонарне електричне поле, напруженість якого на відстані r від осі обертання складає
де B – індукція магнітного поля, ω – кутова швидкість стрижня і v – лінійна швидкість даної точки.  Між напруженістю електричного поля та різницею потенціалів (напругою) існує однозначний зв’язок, який для однорідного поля (${{\vec{E}}}$ = const) виражається співвідношенням (1.20). Але в даній задачі безпосередньо за ним знайти напругу U на кінцях стрижня неможливо, бо напруженість поля E в ньому змінюється від точки до точки, як показано на рис. 11-3. Проте, якщо графік подумки поділити на вузькі смужки шириною Δrі так, аби напруженість Ei в межах однієї смужки можна було вважати однаковою, то за виразом (1.20) напруга на окремій смужці ΔUi ≈ EiΔrі, а на всьому стрижні U ≈ Σ(EiΔrі), що чисельно дорівнює сумарній площі S всіх виділених ділянок на графіку: U ≈ S. Зрозуміло, що при зменшенні ширини смужок точність отриманого виразу буде підвищуватись і в границі Δrі → 0 стане абсолютною. При цьому величина S зрівняється з площею трикутника ΔОАl на графіку. Отже, $U=\frac{1}{2}{{E}_{A}}l$, і, згідно з виразом (1),
|