ФІЗИКА. Вчимося розв'язувати задачі. "ЕЛЕКТРИКА І МАГНЕТИЗМ". Компенсаційний курс
| Сайт: | physics.zfftt.kpi.ua |
| Курс: | physics.zfftt.kpi.ua |
| Книга: | ФІЗИКА. Вчимося розв'язувати задачі. "ЕЛЕКТРИКА І МАГНЕТИЗМ". Компенсаційний курс |
| Напечатано:: | |
| Дата: | Воскресенье, 1 февраля 2026, 10:20 |
Оглавление
- ВСТУП. Електричний заряд та електромагнітне поле
- Розділ І. Електричне поле
- 1. Теоретичні відомості
- 1.1. Напруженість електричного поля. Поле точкового заряду
- 1.2. Принцип суперпозиції. Поле системи зарядів
- 1.3. Потенціал
- 1.4. Зв’язок між напруженістю та потенціалом
- 1.5. Провідники. Електрична ємність, конденсатори
- 1.6. Енергія електричного поля
- 2. Приклади розв’язування задач
- Закон Кулона
- Напруженість і потенціал
- Провідники. Конденсатори
- Робота та енергія електричного поля
- Рівновага й рух зарядів в електричному полі
- 3. Задачі для самостійної роботи
- Закон Кулона
- Напруженість і потенціал
- Провідники. Конденсатори
- Робота та енергія електричного поля
- Рух зарядів в електричному полі
- Розділ ІІ. Постійний електричний струм
- 1. Теоретичні відомості
- 1.1. Характеристики та умови існування електричного струму
- 1.2. Закон Ома
- 1.3. З'єднання резисторів і джерел струму
- 1.4. Робота і потужність електричного струму
- 1.5. Електроліз
- 2. Приклади розв'язування задач
- Характеристики електричного струму
- Електричний опір. З'єднання резисторів
- Закон Ома
- Робота і потужність струму
- Електроліз
- 3. Задачі для самостійної роботи
- Розділ ІІІ. Магнітне поле та електромагнітна індукція
- 1. Теоретичні відомості
- 1.1. Вектор індукції магнітного поля
- 1.2. Дія магнітного поля на рухомі заряди
- 1.3. Провідники зі струмом у магнітному полі
- 1.4. Електромагнітна індукція
- 1.5. Одиниці магнітних величин
- 2. Приклади розв'язування задач
- Індукція магнітного поля
- Рух заряджених частинок у магнітному полі
- Провідники зі струмом у магнітному полі
- Явище електромагнітної індукції
- 3. Задачі для самостійної роботи
ВСТУП. Електричний заряд та електромагнітне поле
|
Усі сили, що спостерігаються в природі й використовуються людиною, є проявами всього чотирьох фундаментальних (таких, що не зводяться до інших) взаємодій: гравітаційної, електромагнітної, сильної (ядерної) та слабкої. При цьому останні дві спостерігаються лише на субмікроскопічних відстанях і є відповідальні за процеси в ядрах атомів та при зіткненнях елементарних частинок надвисоких енергій. Тож усі властивості тіл і явища (крім гравітації), що спостерігаються на відстанях масштабу атома й більше, мають електромагнітну природу. Зокрема це стосується ’’механічних“ (пружність і тертя та хімічних процесів і оптичних явищ. Гравітація або ’’всесвітнє тяжіння“ існує між будь-якими матеріальними об'єктами. Але електромагнітна взаємодія спостерігається тільки між частинками, що мають електричний заряд. Такими зокрема є електрони та протони – частинки, що входять до складу атомів речовини. Електричний заряд є й ознакою, й фізичною величиною – кількісною мірою електромагнітної взаємодії. Одиницею електричного заряду є кулон (1Кл). Заряд є невіддільною від частинки характеристикою. Тому зазвичай говорять не про ’’взаємодію частинок, які мають електричний заряд“, а просто про взаємодію зарядів. Природу електричного заряду ще достеменно не встановлено, але його властивості є добре вивчені. Головні з них такі: 1. Існує два види заряду, що називаються позитивним і негативним. При цьому однойменні заряди відштовхуються, а різнойменні притягаються. 2. Заряд – дискретна величина. Усі заряджені елементарні частинки, що можуть існувати у вільному стані, зокрема електрони і протони, що входять до складу атомів і молекул, мають заряди однакової величини е = ± 1,6·10–19 Кл, яка називається елементарним зарядом. Тому заряд усякого макроскопічного тіла теж є дискретним. Одначе через гранично малу величину е та велику кількість молекул у тілі можна вважати, що заряд у ньому розподіляється неперервно і може змінюватися на будь-яку величину. 3. Для заряду виконується універсальний закон збереження:
|
|
Взаємодія між зарядженими частинками здійснюється не безпосередньо, а передається від точки до точки із скінченною швидкістю і здійснюється через електромагнітне поле, що існує навколо кожного заданого заряду й діє на будь-який інший заряд. У загальному випадку сила електромагнітної взаємодії залежить від величини зарядів, їхнього взаємного розташування та стану руху. Але ця залежність є такою, що електромагнітну силу \(\vec{F}\) завжди можна розділити на дві складові – електричну \(\vec{F}_{e}\) і магнітну \(\vec{F}_{м}\) так, що
При цьому електрична сила визначається величиною і просторовим розташуванням зарядів, а магнітна – їхнім станом руху. Відповідно й електромагнітне поле можна трактувати як сукупність електричного та магнітного полів. Така можливість є дуже зручною й продуктивною, але не означає існування в природі двох окремих названих полів. Тож електричне та магнітне поля є двома різними проявами єдиного електромагнітного поля. |
Незаперечним свідченням цього є здатність електричного та магнітного полів до взаємного перетворення. Але в цьому розділі розглядаються властивості лише електричного поля заряджених частинок.
Більш детально електромагнітна взаємодія та електромагнітні явища розглядаються в наступних розділах:
ІІ. Постійний електричний струм
ІІІ. Магнітне поле та електромагнітна індукція
Кожен розділ містить:
1. Короткі теоретичні відомості
2. Приклади розв’язування задач
3. Задачі для самостійної роботи
1. Теоретичні відомості
Властивості електричного поля визначаються величиною та просторовим розташуванням зарядів, які його створюють. У чистому вигляді вони виявляють себе в електростатичних полях, тобто таких, які створюються нерухомими зарядженими частинками й тілами.
Далі розглянуто наступні питання:
1.1. Напруженість електричного поля. Поле точкового заряду
1.2. Принцип суперпозиції. Поле системи зарядів
1.4. Зв’язок між напруженістю та потенціалом
1.1. Напруженість електричного поля. Поле точкового заряду
Дослід свідчить, що сила, що діє в полі на внесений заряд, є прямо пропорційна до його величини. Тому її відношення до величини заряду залежить тільки від поля і є його кількісною характеристикою — напруженістю. За означенням
|
|
напруженістю електричного поля \(\vec{E}\) називається відношення сили \(\vec{F}\), що діє на внесений у дану точку поля позитивний пробний заряд, до його величини qпр : |
|
|
\(\vec{E}=\frac{\vec{F}}{q_{пр}}\). |
(1.1) |
(“Пробний заряд“– це точковий заряд малої величини q, який практично не впливає на заряди, що створюють досліджуване поле.)
Вектор \(\vec{E}\) є збігається з вектором сили, що діє на одиничний позитивний заряд, внесений у дану точку поля, отже,
напруженість є силовою характеристикою електричного поля
і визначає силу, що діє у полі на заданий точковий заряд q згідно з формулою:
|
|
\(\vec{F}=q\vec{E}\). |
(1.2) |
Напрямок вектора\(\vec{F}\) залежить від знаку заряду: сила, що діє на позитивний заряд є збіжною, а на негативний – антипаралельною до напрямку поля, рис. 1.1.

Одиницею напруженості електричного поля є 1 В/м ("вольт-на-метр" ).
(Варто зауважити, що ця одиниця ґрунтується не на означенні (1.1), як зазвичай, а на зв’язку напруженості з потенціалом (формула (1.20)). Проте, як і має бути, в полі з напруженістю 1 В/м на заряд 1 Кл діє сила 1 Н).
Напруженість \(\vec{E}\), тож і силу \(\vec{F}\), що діє на заряд у полі, можна визначати теоретично, не вдаючися до безпосередніх вимірів. Це дозволяє розраховувати рух заряджених частинок в електричному полі, на чому ґрунтується конструювання електричних та електронних пристроїв.
Існують різні способи розрахунку напруженості електричних полів, які прямо чи опосередковано спираються на два встановлені на досліді основні положення: закон Кулона та принцип суперпозиції.
Закон Кулона визначає взаємодію між точковими зарядами й гласить:
|
Два точкові заряди у вакуумі взаємодіють між собою із силою, що є прямо пропорційна добуткові величин зарядів q1q2 і обернено пропорційна квадратові відстані r між ними: |
|
${{{F}_{0}}}=k\frac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$. |
(1.3) |
Числове значення коефіцієнта пропорційності k залежить від обраної системи одиниць і в системі СІ складає
k = 9·109 м/Ф.
Коефіцієнт k є зручним для обчислень, але в теорії прийнято використовувати електричну сталу ε0 , що дорівнює
ε0 = (1/4πk) = 8,85·10–12 Ф/м.
Відповідно, розгорнутий вираз закону Кулона має вигляд:
|
$F=\frac{{{q}_{1}}{{q}_{2}}}{4\pi {{\varepsilon }_{0}}{{r}^{2}}}$. |
(1.3а) |
В однорідному ізотропному діелектрику (непровідному середовищі) сила взаємодії між зарядами F зменшується порівняно із силою взаємодії у вакуумі F0, так що
|
$F=\frac{{{F}_{0}}}{\varepsilon }$, |
(1.4) |
де коефіцієнт послаблення ε називається діелектричною проникністю речовини і є її табличною характеристикою. (Проте для газів, окрім надвисокого тиску, вона практично дорівнює одиниці).
Таким чином, для поля в діелектрику формули (1.3) і (1.3а) набувають вигляду:
|
$F=k\frac{{{q}_{1}}{{q}_{2}}}{{\varepsilon }{{r}^{2}}}=\frac{{{q}_{1}}{{q}_{2}}}{4\pi {{\varepsilon }_{0}}{\varepsilon }{{r}^{2}}}$. |
(1.5) |
Напрями сил взаємодії між двома зарядами визначаються їхніми знаками: однойменні заряди відштовхуються (рис. 1.2 а,б), а різнойменні – притягаються (рис. 10.2в) по лінії їхнього розташування.

Прийнявши у формулах (1.3), (1.3а) один із зарядів за заряд q, що створює електричне поле, а інший – за пробний заряд qпр, з означення (1.1) дістанемо загальний вираз для величини (модуля) напруженості електричного поля точкового заряду:
|
|
$E=k\frac{q}{\varepsilon {{r}^{2}}}=\frac{q}{4\pi {{\varepsilon }_{0}}\varepsilon {{r}^{2}}}$, |
(1.6) |
інакше
|
${E}=\frac{{{E}_{0}}}{\varepsilon }$. |
(1.6а) |
Напрям вектора \(\vec{E}\) визначається знаком заряду: для позитивного заряду він скрізь напрямлений радіально від заряду, а для негативного – до заряду (рис. 1.3).

1.2. Принцип суперпозиції. Поле системи зарядів
Дослід свідчить, що електричні поля не взаємодіють між собою – вони діють на заряди, але не одне на одного. Це відображує принцип суперпозиції, за яким
|
вектор напруженості електричного поля довільної системи зарядів у кожній точці дорівнює сумі векторів напруженості полів, створюваних у цій точці кожним із зарядів системи окремо (за відсутності інших): |
||
|
|
\(\vec{E}=\vec{E}_{1}+\vec{E}_{2}+…+\vec{E}_{n}=\sum\limits_{i=1}^{n}\vec{E}_{i}\). |
(1.7) |
Принцип суперпозиції разом із законом Кулона дозволяє визначати характеристики полів, що створюються як дискретними сукупностями зарядів, так і протяжними зарядженими тілами.
Поле системи точкових зарядів можна розрахувати безпосередньо за виразом (1.7). Для цього в ньому слід за формулою (1.6) визначити модулі Еі та додати самі вектори \(\vec{E}_{i}\), як це ілюструє рис. 1 .4 для найпростішої системи – двох точкових зарядів.

Подібно розраховують і поле протяжного зарядженого тіла: його подумки поділяють на елементарні (точкові) ділянки, відтак на основі формули (1.6) записують вираз напруженості поля окремої ділянки і відповідними математичними методами додають (інтегрують) напруженості полів усіх ділянок. При цьому для тіл правильної форми із симетричним розподілом заряду виходять прості загальні формули, як у наступних прикладах.
Поле сферичної оболонки. При рівномірному розподілі заряду q по поверхні сфери радіуса R створюється електричне поле, що скрізь має радіальний напрям і назовні (на відстанях r ≥ R від центра) збігається з полем розміщеного в центрі точкового заряду такої самої величини q і має таку саму напруженість E (формула (1.6)). Зокрема на поверхні
|
$E_{R}=\frac{q}{4\pi {{\varepsilon }_{0}}R^{2}}$. |
(1.8) |
Всередині сфери (r < R), як показано на рис. 1.5а, поле відсутнє:
|
$\vec{E}$ = 0. |
(1.8а) |
Поле кулі радіуса R із рівномірно розподіленим по об'єму зарядом q назовні (на відстанях від центра r ≥ R ) теж збігається з полем точкового заряду й визначається формулою (1.6), а всередині (r < R) лінійно зростає від 0 в центрі до значення (1.8) на поверхні (рис. 1. 5б).
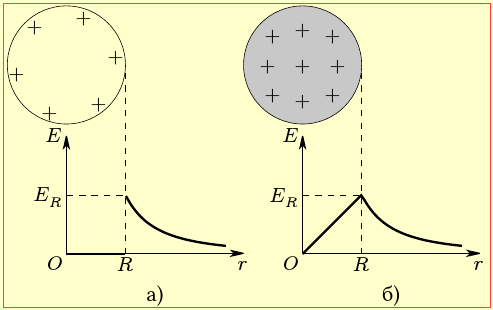
Стосовно наведених положень варто сказати наступне. Радіальний напрям полів розглянутих тіл легко встановити на основі принципу суперпозиції, подумки розсікаючи їх паралельними площинами на множину кілець чи дисків, і враховуючи, що поля таких складових елементів є спрямовані вздовж діаметра сфери чи кулі. Що ж до формул, то отримати їх методами елементарної фізики не можна. Але на підтримку виразу (1.8а) можна вказати, що всередині будь-якої зарядженої замкненої поверхні напрямки полів двох малих ділянок на кінцях однієї хорди є зустрічними.
Поле рівномірно зарядженої нескінченної площини. З огляду на міркування симетрії можна зрозуміти, що таке поле є однорідне (\(\vec{E}\) = const) і спрямоване перпендикулярно до площини (рис. 1.6а). Величина його напруженості визначається наступною простою формулою, яку, проте теж не можна отримати елементарно:
|
|
$E=\frac{\sigma }{2{{\varepsilon }_{0}}\varepsilon }$, |
(1.9) |
де
|
|
$\sigma =\frac{\Delta q}{\Delta S}$ |
|
– поверхнева густина заряду (Кл/м2), тобто заряд, що припадає на одиницю площі зарядженої поверхні.
Примітка. Нескінченна площина – то є абстракція. Проте практично таке саме поле створює й реальна плоска пластина на малих порівняно з її розмірами відстанях.
У випадку двох паралельних заряджених площин напруженість поля за принципом суперпозиції визначається як \(\vec{E}\) = \(\vec{E}_{1}\) + \(\vec{E}_{2}\) і є не однаковою між та поза пластинами. Зокрема, напруженість поля плоского конденсатора (див. п.1.5), де знаки зарядів є різні, а величина σ однакова, поле поза пластинами відсутнє, а між ними – спрямоване від ”+“ до ”–“ (рис. 1.6б) і має напруженість рівну подвоєній напруженості поля одної пластини:
|
$E=\frac{\sigma }{{{\varepsilon }_{0}}\varepsilon }$. |
(1.10) |
1.3. Потенціал
|
Потенціал. Сила, що діє на заряджену частинку в заданому електричному полі, визначається тільки величиною її заряду та координатами . Тому (див. [І], п. 4.2) робота поля при переміщенні частинки між будь-якими точками 1 і 2, не залежить від пройденого шляху і дорівнює спадові її потенціальної енергії:
Ця робота є прямо пропорційна силі (1.2), що діє на частинку, тож і її зарядові. Тому
Указану різницю потенціалів інакше називають спадом напруги, або просто напругою й позначають одним символом:
Отже, вираз роботи електростатичного поля при переміщенні заряду має вигляд:
або
Різниця потенціалів (напруга) вимірюється у вольтах (В), 1 В = 1 Дж/Кл – це різниця потенціалів у таких двох точках поля, при переміщенні між якими заряду q = 1 Кл виконується робота A = 1 Дж. Для елементарних частинок, зокрема електронів, джоуль є загрубою мірою роботи та енергії, й натомість використовують зручнішу позасистемну одиницю – електронвольт (еВ). За означенням
|
|
Таким чином,
Співвідношення (1.12) визначає тільки різницю потенціалів між заданими точками. А сам потенціал і потенціальна енергія є визначеними тільки відносно обраного нульового рівня – точки (чи множини точок), де потенціал приймається рівним нулю. Зважаючи на це, можна дати наступне означення:
Інакше кажучи,
При цьому вибір нульової точки є довільним і визначається лише міркуваннями зручності. До прикладу, в електротехніці та електроніці нульову точку потенціалу обирають на земній поверхні, а в фізиці – на "на нескінченності", тобто в точках, що знаходяться безмежно далеко від зарядів, які створюють поле. Обчислення потенціалу ґрунтується на принципом суперпозиції, за яким
Для маленького зарядженого тіла (точкового заряду) потенціал визначає наступна формула потенціалу поля точкового заряду:
або
|
||||||||||||||||||||||
|
\(\varphi =k\sum{\frac{{{q}_{i}}}{\varepsilon {{r}_{i}}}}\). |
(1.17) |
|
За розглянутою схемою визначають і потенціал поля протяжного зарядженого тіла: спочатку його ''розбивають'' на малі (точкові) ділянки, а потім відповідно до виразу (1.15) методами вищої математики визначають сумарний потенціал і за симетричного розподілу заряду отримують відповідну формулу. Зокрема, потенціал поля сфери радіуса R із зарядом q, який рівномірно розподілено по поверхні або об'єму, назовні (на відстанях r ≥ R від центра) збігається з потенціалом поля точкового заряду, розміщеного в центрі, й за формулами (1.16) та (1.16а), відповідно, дорівнює
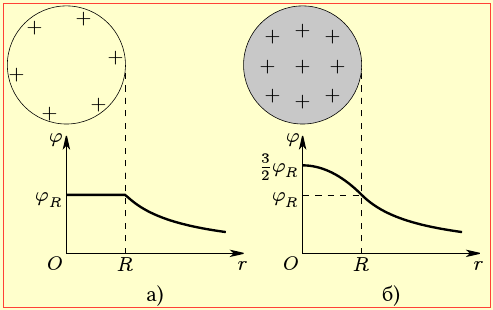
Всередині через відсутність поля (див. п. 1.2) потенціал є скрізь однаковий і збігається з потенціалом поверхні:
Графік залежності φ(r) для поля сфери показано на рис. 1.9 а. Такою самою (1.18) є й залежність φ(r) назовні (r ≥ R) рівномірно зарядженої по об'єму провідної кулі, позаяк в ній надлишковий заряд завжди зосереджено на поверхні. Вираз (1.18) і відповідний графік φ(r) лишаються чинними й назовні (r ≥ R) рівномірно зарядженої по об'єму кулі з діелектрика. Але всередині через зменшення напруженості потенціал у напрямку центра зростає, як показано на рис. 1.7. |
1.4. Зв’язок між напруженістю та потенціалом
Між напруженістю \(\vec{E}\) та потенціалом φ існує тісний зв’язок, який можна з'ясувати на прикладі роботи однорідного електричного поля \(\vec{E}\) = const на переміщенні $\Delta \vec{r}$ якогось заряду q між заданими точками 1 і 2 (рис. 1.8).
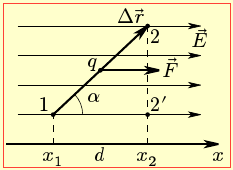
Ця робота через напруженість визначається як A = F·Δr·cosα = qE(x2 – x1) і як Α = q(φ1 − φ2) – через потенціал. Отже,
|
${{E}}=-\frac{{{\varphi }_{2}}-{{\varphi }_{1}}}{{{x}_{2}}-{{x}_{1}}}$, |
(1.19) |
або лаконічніше
|
$E=\frac{U}{d}$, |
(1.20) |
де E — модуль напруженості, U = φ1 − φ2 — спад напруги між точками 1 і 2, d = x2 – x1 — відстань між ними, відрахована в напрямку поля.
Аби сформулювати загальний зміст отриманого результату, зважимо на таке:
1. Вираз (1.19) є чинним при будь-якому взаємному розташуванні точок 1 і 2. При цьому коли кут α гострий (як на рис. 1.8), то φ1 > φ2, а коли тупий – навпаки, φ2 > φ1. Це означає, що в напрямку поля потенціал завжди зменшується.
2. При переміщенні заряду з т. 2 вздовж відрізка 2-2′ кут α = 90°, тож А = 0 і φ2 = φ2′. Це стосується й усіх інших точок площини, що проходить через т.2 перпендикулярно до напрямку поля.
3. Величина d = Δr·|cosα| є найменшою можливою відстанню між точками із заданою різницею потенціалів. Отже, вздовж напрямку поля швидкість зміни потенціалу Δφ/Δx є найбільшою.
Таким чином,
|
вектор напруженості електричного поля є скрізь напрямлений в бік найшвидшого зменшення потенціалу й по модулю дорівнює цій швидкості |
|
Слід зауважити, що це співвідношення встановлено тут для однорідного поля (\(\vec{E}\) = const ), тож у випадку неоднорідного поля (\(\vec{E}\) ≠ const) вираз (1.20) є непридатним для обчислень. Але, попри це, він якісно правильно відображає властивості поля й у загальному випадку. Зокрема те, що
|
про присутність електричного поля в заданій точці свідчить не наявність у ній певного потенціалу \(\varphi\), а лише його зміна \(\Delta\varphi\) ≠ 0 при переміщенні в сусідні точки. |
До прикладу, коли \(\varphi\ne{0}\), але \(\Delta\varphi=0\), то електричне поле відсутнє (\(\vec{E}=0\)). І навпаки, якщо в певній області простору із зарядженими тілами напруженість поля \(\vec{E}=0\), то це означає не нульову величину потенціалу, а лише його сталість (φ = const) у цій області.
Із співвідношення (1.20) також випливає, що
|
на межі двох середовищ не можливі стрибки потенціалу, |
бо це означало би необмежено велику напруженість поля.
Задля наочності електричне поле часто "зображують" на рисунку у вигляді сукупностей силових ліній та еквіпотенціальних поверхонь.
Силовою лінією (інакше – лінією поля) називається лінія, дотична до якої в кожній точці збігається з напрямом вектора напруженості поля в цій точці.
Еквіпотенціальною поверхнею (або поверхнею рівного потенціалу) називається поверхня, у всіх точках якої потенціал поля має однакове значення.
При будь-якому переміщенні еквіпотенціальною поверхнею у виразі (1.13) \(\cos\alpha=0\) і \(\alpha=90^{\circ}\). Це означає, що
|
силові лінії та еквіпотенціальні поверхні є взаємно ортогональні, тобто вектор \(\vec{E}\) у кожній точці поля спрямовано по нормалі до еквіпотенціальної поверхні, що проходить через цю точку. |
До прикладу, для поля точкового заряду (рис. 1.9 а, б) силові лінії є радіальними променями, а еквіпотенціальні поверхні – концентричними сферами (на рисунку – колами). Для однорідного поля силові лінії є паралельними рівновіддаленими променями, а еквіпотенціальні поверхні – перпендикулярними до них рівновіддаленими площинами (рис.1.9в). У зв'язку з цим зауважимо, що величина d у виразі (1.20) – то є відстань між двома заданими еквіпотенціальними поверхнями однорідного електричного поля.

1.5. Провідники. Електрична ємність, конденсатори
|
Провідниками називаються речовини, що добре проводять електричний струм: тверді метали, валентні електрони котрих є практично вільними, розплави й електроліти (розчини, в яких молекули є дисоційовані) та йонізовані гази. Наявність великої кількості практично вільних зарядів зумовлює характерну поведінку провідників при вміщенні в електростатичне поле та при електризації (створенні в них надлишку зарядів певного знаку). А саме, через велику рухливість надлишкові заряди під дією зовнішнього поля та кулонівського відштовхування виходять на поверхню провідника й розподіляються по ній так, аби припинився впорядкований рух і встановилася рівновага зарядів. Отже, за будь-яких умов в об'ємі провідника електростатичне поле відсутнє (\(\vec{E}=0\)), а на поверхні в кожній точці напрямлене по нормалі до неї. Це означає, що поверхня провідника є еквіпотенціальною поверхнею електричного поля (φ = const), незалежно від того, якими зарядами воно створюється. |
|
Дослід свідчить, що заряд відокремленого (віддаленого на велику відстань від інших тіл) провідника та його потенціал пов'язані прямою пропорційною залежністю \(q=C\varphi\). При цьому величина
називається електричною ємністю (або просто ємністю) провідника і залежить тільки від його розмірів і форми та діелектричної проникності середовища, в якому він перебуває. Прикладом може слугувати ємність провідної кулі або сфери, котра згідно з виразом (1.18), складає
За наявності навколишніх тіл потенціал і ємність окремого провідника не є однозначно визначеною й залежить від їхнього взаємного розташування. Але такої вади не має конденсатор – сукупність провідних пластин-обкладок (зазвичай двох), зазор між якими є набагато менший за їхні розміри й звичайно є заповнений діелектриком. За такої умови подані на обкладки різнойменні заряди однакової величини створюють електричне поле, що існує практично тільки всередині конденсатора. Тому конденсатор є нечутливий до оточення та зовнішніх полів. Ємність конденсатора визначається відношенням його заряду до напруги:
де величина q – заряд позитивної обкладки, а напруга U – модуль різниці потенціалів між ними. Профіль обкладок конденсатора, в принципі, може бути довільним, але реально використовують три види конденсаторів: плоскі, сферичні та циліндричні. Плоский конденсатор складається з двох однакових паралельних плоских металевих пластин певної площі S кожна, котрі розміщені на відстані \(d<<\sqrt{S}\) одна від одної. Тому вважається, що в конденсаторі заряди рівномірно розподіляються по обкладках із густиною
так що електричне поле в ньому є однорідним і має напруженість (формула (1.10))
Отже, ємність плоского конденсатора, згідно з означенням (1.23) та співвідношенням (1.20), визначається формулою
Сферичний конденсатор являє собою дві концентричні сферичні оболонки з радіусами R1 і R2 > R1, простір між якими зазвичай заповнено діелектриком із проникністю ε. Тож, виразивши напругу U = φ1 – φ2 через потенціали обкладок (формула (1.18)), дістанемо наступну формулу ємності сферичного конденсатора
На електричних схемах конденсатор зображується, як показано на рис.10.
|
|
На практиці, крім поодиноких конденсаторів, використовують їхні з'єднання, найпростішими з яких є послідовне та паралельне (рис. 11а, 11б, відповідно).
При послідовному з'єднанні напруга U на з'єднанні дорівнює сумі напруг Ui на кожному з конденсаторів:
При цьому заряди qі на окремих конденсаторах та всьому з'єднанні є однакові:
Тож, відповідно до означення (1.23), ємність послідовного з'єднання конденсаторів задовольняє співвідношення
Зокрема, для послідовного з'єднання n конденсаторів однакової ємності С
а для двох конденсаторів C1 і C2
При паралельному з'єднанні напруги Uі на окремих конденсаторах та всьому з'єднанні U0 є однакові:
а сумарний заряд системи q0 дорівнює сумі зарядів qі окремих конденсаторів:
Отже, ємність паралельного з'єднання конденсаторів дорівнює сумі їхніх ємностей:
Для n конденсаторів однакової ємності C
|
1.6. Енергія електричного поля
Заряди, що створюють електричне поле, діють не лише на внесені в поле інші заряди, а й один на одного. Тому будь-яка система зарядів має відповідну енергію взаємодії між ними. Ця енергія дорівнює роботі зовнішніх сил по об'єднанню відокремлених зарядів у систему й дорівнює сумі енергій взаємодії всіх пар зарядів, які входять до її складу. Зокрема, енергія взаємодії двох точкових зарядів q1 і q2, що розташовані один від одного на відстані r у середовищі з діелектричною проникністю ε, визначається формулою
|
$W=\frac{{{q}_{1}}{{q}_{2}}}{4\pi {{\varepsilon }_{0}}\varepsilon r}$.
|
(1.30) |
Цей вираз можна записати симетрично як
|
$W=\frac{1}{2}\left( {{q}_{1}}\frac{{{q}_{2}}}{4\pi {{\varepsilon }_{0}}\varepsilon }+{{q}_{2}}\frac{{{q}_{1}}}{4\pi {{\varepsilon }_{0}}\varepsilon } \right)$, |
|
або
|
\(W=\frac{1}{2}(q_{1}\varphi_{1}+q_{2}\varphi_{2})\), |
|
де, відповідно до формули (1.16), \(\varphi_{1}\) – потенціал поля заряду q2 у точці розташування заряду q1, а \(\varphi_{2}\) – потенціал поля заряду q1 у точці розташування заряду q2. Отже,
енергія взаємодії системи n точкових зарядів qi
визначається загальним виразом
|
\(W =\frac{1}{2}\sum\limits_{i=1}^{n}q_{i}\varphi_{i}\), |
(1.31) |
де \(\varphi_{i}\) – потенціал поля решти зарядів у місці розташування заряду qi.
Конкретне значення W залежить від величини та просторового розташування зарядів. Зокрема, енергія зарядженого конденсатора визначається однією з формул:
|
\(W=\frac{q^{2}}{2C}\); |
(1.32а) |
|
\(W=\frac{CU^{2}}{2}\); |
(1.32б) |
|
\(W=\frac{qU}{2}\). |
(1.32в) |
Енергію плоского конденсатора можна виразити й через напруженість його поля Е, якщо у формулі (1.32б) напругу замінити за співвідношенням (1.20) а ємність – за формулою (1.26):
|
$W=\frac{1}{2}\cdot \frac{\varepsilon {{\varepsilon }_{0}}S}{d}\cdot {{\left( Ed \right)}^{2}}=\frac{\varepsilon {{\varepsilon }_{0}}{{E}^{2}}}{2}V$, |
(1.33) |
де V = Sd.
Величина V є об'ємом, який займає електричне поле зарядженого конденсатора. Це наводить на думку, що енергія конденсаторає є не локалізована на пластинах, а розподілена в полі так, що W = wV, де
|
$w=\frac{\varepsilon {{\varepsilon }_{0}}{{E}^{2}}}{2}$ |
(1.34) |
– об'ємна густина енергії електричного поля (Дж/м3), тобто, енергія, що міститься в одиниці об'єму поля.
Це твердження не спростовується жодним із відомих фактів і є чинним не лише для конденсатора, а й для будь-якої системи зарядів. Тому, загальновизнано, що
електричне поле як таке має енергію, котра є розподілена в просторі з об'ємною густиною, залежною від напруженості поля та діелектричної проникності середовища.
2. Приклади розв’язування задач
При розв'язуванні задач електростатики необхідно враховувати загальні поради по організації й оформленню розв'язку (див. "Етапи розв'язування задач").
Наведені приклади розв'язування задач поділені на такі групи:
Закон Кулона
Задача 1.1. Три нерухомі точкові заряди q1 = 2 нКл, q2 = 5 нКл, q3 = –3 нКл закріплен0 у вершинах правильного трикутника зі стороною a = 10 см. Визначити сили F1, F2, F3, що діють на кожен із зарядів з боку двох інших.
Задача 1.2. Коли дві заряджені металеві кульки одного розміру дотикнули одну до одної й розвели на вдвічі більшу відстань r, сила взаємодії F між ними стала вдвічі меншою. Визначити відношення зарядів кульок (q1/q2).
Задача 1.3. Дві однакові металеві кульки, що підвішені в одній точці на нитках однакові довжини, занурюють у рідину з густиною в n = 3 рази меншою, ніж у кульок. Визначити діелектричну проникність ε рідини, якщо при зануренні кульок кут розходження ниток не змінився.
Задача 1.4. За уявленнями класичної механіки електрони в атомах рухаються навколо ядер по визначених орбітах, як планети навколо Сонця. Виходячи з цього, знайти швидкість v руху електрона в атомі Гідрогену, якщо радіус його колової орбіти r = 53 пм.
Задача 1.1
Три нерухомі точкові заряди q1 = 2 нКл, q2 = 5 нКл, q3 = –3 нКл закріплено у вершинах правильного трикутника зі стороною a = 10 см.
Визначити
сили F1, F2, F3, що діють на кожен із зарядів з боку двох інших.
|
Дано: \(q_{1}\) = 2 нКл = 2·10–9 Кл
\(q_{2}\) = 5 нКл = 5·10–9 Кл
\(q_{3}\) = –3 нКл = –3·10–9 Кл
|
|
F1 - ? F2 - ? F3 - ?
|
Розв'язання
Шукані сили є рівнодійними сил, що діють на кожний заряд з боку двох інших (рис. 1) і визначаються формулою (1.3). Тож, позаяк напрями складових сил відомі, для розрахунків доцільно використати теорему косинусів. Тоді маємо:
двох інших (рис. 1) і визначаються формулою (1.3). Тож, позаяк напрями складових сил відомі, для розрахунків доцільно використати теорему косинусів. Тоді маємо:
${{F}_{1}}=\frac{k{{q}_{1}}}{{{a}^{2}}}\sqrt{q_{2}^{2}+q_{3}^{2}+{{q}_{2}}\left| {{q}_{3}} \right|\cos {{\alpha }_{1}}}$,
де \(\alpha_{1}=120{}^\circ \) – кут між векторами \(\vec{F}_{12}\) і \(\vec{F}_{13}\) сил, які діють на заряд q1 з боку q2 і q3.
Аналогічно виражається й решта сил.
Далі, задля зручності позначвши величину зарядів як q = Q·10–9 Кл, де Q1 = 2, Q2 = 5, Q3 = –3, та врахувавши числові значення k = 4π·10–9 Ф/м, a2= 10–2 м2, cosα1 = cosα2 = –0,5, cosα3= 0,5, отримаємо наступні відповіді:
F1 = 1,8Q1·$\sqrt{Q_{2}^{2}+Q_{3}^{2}-{{Q}_{2}}\left| {{Q}_{3}} \right|}$ (мкН) = 7,85 мкН;
F2 = 1,8Q2·$\sqrt{Q_{1}^{1}+Q_{3}^{2}-{{Q}_{1}}\left| {{Q}_{3}} \right|}$ (мкН) = 11,9 мкН;
F3 = 1,8Q1·$\sqrt{Q_{1}^{2}+Q_{2}^{2}+{{Q}_{1}} {{Q}_{2}} }$ (мкН) = 33,7 мкН.
Задача 1.2
Коли дві заряджені металеві кульки одного розміру дотикнули одну до одної й розвели на вдвічі більшу відстань r, сила взаємодії F між ними стала вдвічі меншою.
Визначити
початкове відношення зарядів кульок (q1/q2).
|
Дано: (r2/r1) = 2
(F1/F2) = 2
|
| (q1/q2)-? |
Розв'язання
Позаяк кульки металеві й однакові за розміром, після дотикання вони матимуть однакові за знаком заряди величиною
|
$q=\frac{\left| {{q}_{1}}\pm {{q}_{2}} \right|}{2}$, |
|
де знак ”–“ стосується випадку q1q2 < 0 (заряди різнойменні). Отже, виразивши сили взаємодії між кульками за формулою (1.3), отримаємо:
$\frac{{{F}_{1}}}{{{F}_{2}}}=\frac{4{{q}_{1}}{{q}_{2}}}{{{\left( {{q}_{1}}\pm {{q}_{2}} \right)}^{2}}}\cdot {{\left( \frac{{{r}_{2}}}{{{r}_{1}}} \right)}^{2}}$.
Звідси, увівши позначення (q1/q2) = x і врахувавши задані співвідношення сил та відстаней, отримаємо такі можливі рівняння для визначення відношення величин зарядів x:
|
2x2 + 3x + 2 = 0 |
(1) |
|
2x2 – 5x + 2 = 0 |
(2) |
Не важко знайти, що перше рівняння не має дійсних розв'язків, а корені другого складають:
x1 = 2; x2 = $\frac{1}{2}$.
Це означає що,
заряди кульок мають різні знаки й удвічі відрізняються за величиною.
Наявність двох можливих значень величини x може справити хибне враження, що відповідь є неоднозначною. Але наявність у рівняння (2) двох дійсних коренів відображує лише те, що будь-яку з кульок можна розглядати і як першу, і як другу.
Задача 1.3
Дві однакові металеві кульки, що підвішені в одній точці на нитках однакові довжини, занурюють у рідину з густиною в n = 3 рази меншою, ніж у кульок.
Визначити
діелектричну проникність ε рідини, якщо при зануренні кульок кут розходження ниток не змінився.
|
Дано: n = 3
|
|
ε - ?
|
Розв'язання
За означенням (формула (1.4)) діелектрична проникність дорівнює відношенню сил кулонівської взаємодії кульок у повітрі F1 та у рідині F2 (рис. 3):
|
$\varepsilon =\frac{{{F}_{1}}}{{{F}_{2}}}$. |
(1) |
Для визначення величини ε візьмемо до уваги, що кульки перебувають у рівновазі, тобто всі сили, що діють на кожну кульку, в сумі дорівнюють нулю. У повітрі це сила кулонівського відштовхування \(\vec{F}_{1}\), сила тяжіння \(m\vec{g}\) та сила натягу нитки \(\vec{T}_{1}\) , отже
|
\(m\vec{g}+\vec{T}_{1}+\vec{F}_{1}\) = 0 \(\Rightarrow \) ${{\vec{F}}_{1}}=-\left( m\vec{g}+{{{\vec{F}}}_{2}} \right)$ |
і, як зрозуміло з рис 3а,
|
F1 = mg·tgα. |
(2) |
 |
При зануренні в рідину крім зазначених сил з’являється ще й виштовхувальна сила Архімеда (рис.3б) \(\vec{F}_{A}\) ([1], п. 6.2). Тож по аналогії з попереднім для сили \(\vec{F}_{2}\) можна записати:
$m\vec{g}+{{\vec{T}}_{2}}+{{\vec{F}}_{2}}+{{\vec{F}}_{A}}=0$
і
|
F2 = (mg – FА)tgα. |
(3) |
Відтак, підставивши сили (2) і (3) у формулу (1) та виразивши їх через густини рідини ρ0 та кульки ρ = nρ0, отримаємо відповідь:
$\varepsilon =\frac{\rho Vg}{\rho Vg-{{\rho }_{0}}Vg}=\frac{n}{n-1}$ = 1,5.
Задача 1.4.
За уявленнями класичної механіки електрони в атомах рухаються навколо ядер по визначених орбітах, як планети навколо Сонця. Виходячи з цього,
знайти
швидкість v руху електрона в атомі Гідрогену, якщо радіус його колової орбіти r = 53 пм.
|
Дано: r = 5,3·10-11 м
|
|
v - ?
|
Розв'язання
Кулонівська сила (1.3а), під дією якої електрон рухається по коловій орбіті, є доцентровою ([І], формули (1.28), (2.17)), тож за другим законом Ньютона
\(\frac{e^{2}}{4\pi\varepsilon_{0}r^{2}}=\frac{mv^{2}}{r}\),
і
|
\(v=\frac{e}{2\sqrt{\pi {{\varepsilon }_{0}}rm}}\). |
|
Урахувавши величину заряду e = 1,6·10-19 Кл і маси m = 9,1·10-31 кг електрона та знаяення ε0 = 8,85·10–12 Ф/м, отримаємо
v = 2,18·106 м/с.
Напруженість і потенціал
|
Задача 1.5. Електричне поле створюється двома однаково зарядженими малими кульками, що розміщені у вершинах правильного трикутника зі стороною a = 10 см. Визначити вектор напруженості поля \(\vec{E}\) в третій вершині, якщо в ній потенціал φ = 10 В. |
|
Задача 1.6. У вершинах правильного трикутника зі стороною a = 10 см закріплено точкові заряди q1 = 1нКл, q2 = –2q1 і q3 = –3 q1. Визначити напруженість \(\vec{E}_{0}\) електричного поля в центрі трикутника. |
|
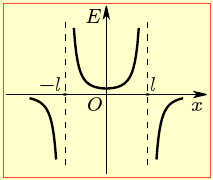
Задача 1.7. Точкові заряди q і –q розташовано на осі OX на відстані 2l один від одного. Визначити та показати на графіку залежність Ex(x) проєкції напруженості електричного поля зарядів на лінії їхнього розташування. |
|
Задача 1.8. Електричне поле створюється металевою кулею радіуса R1 = 1 см із зарядом q = 1 нКл, до якої щільно прилягає сферичний шар діелектрика з проникністю \(\varepsilon=4,5\) і зовнішнім радіусом R2 = 2 см. Визначити та показати на графіках залежності напруженості E(r) і потенціалу φ(r) поля кулі від відстані r до її центра. |
|
Задача 1.9. Дві паралельні пластини із густиною заряду σ1 і σ2 закріплено перпендикулярно до осі ОХ у точках x = 0 і х = d (рис. 9). Уважаючи електричне поле системи однорідним, визначити та показати на графіку залежність від координати x: А) проєкції напруженості Ех(х); Б) потенціалу φ(х), прийнявши φ(0) = 0. Розглянути випадки: 1. σ1 = σ, σ2 = 2σ; 2. σ1 = σ, σ2 = – σ. Задача 1.10. По розміщеному в повітрі тонкому кільцю радіуса R рівномірно розподілено заряд q. Визначити: А) напруженість електричного поля Е на осі кільця в залежності від відстані r до його центра; Б) проаналізувати залежність Е(r) і показати загальний вигляд її графіка. Задача 1.11. Два однакові точкові заряди +q і –q, що закріплені на невеликій відстані l один від одного (рис. 11), утворюють "електричний диполь". Установити вираз залежності його потенціалу \(\varphi \left(r,\vartheta \right)\) в повітрі від відстані до центра r і кута (\vartheta \) за умови \(r\gg l\). |
Задача 1.5
Електричне поле створюється двома однаково зарядженими малими кульками, що розміщені у вершинах правильного трикутника зі стороною a = 10 см.
Визначити
напруженість поля\(\vec{E}_{1}\) в третій вершині, якщо в ній потенціал φ = 10 В.
|
Дано: l = 10 см = 0,1 м
φ = 10 В
|
|
E - ? |
Розв'язання
Відповідно до принципу суперпозиції (1.7), напруженість поля в вершині А трикутника (рис. 5) складає
\(\vec{E}=\vec{E}_{1}+\vec{E}_{2}\),
де \(\vec{E}_{1}\) і \(\vec{E}_{2}\) – вектори напруженості полів кожного із зарядів.
Модуль суми будь-яких двох векторів можна визначити за теоремою косинусів:
|
$E=\sqrt{E_{1}^{2}+E_{2}^{2}+2{{E}_{1}}{{E}_{2}}cos\alpha }$, |
|
де α – кут між додаваними векторами. При однакових зарядах кульок q1 = q2 = q та відстанях від них до т. А напруженості Е2 = Е1. Отже
| $E=2{{E}_{1}}\sqrt{2\left( 1+\cos \alpha \right)}=2{{E}_{1}}\cos \frac{\alpha }{2}$. | (1) |
Отриманий вираз є чинним при будь-якій відстані від зарядів до т. А та куті α. Але для рівностороннього трикутника α = 60°, тож
|
$E={{E}_{1}}\sqrt{3}$, |
(2) |
де напруженість поля одного заряду за формулою (1.6а) дорівнює
\(E_{1}=\frac{kq}{l^{2}}\).
Величину q не задано, але її легко виключити за допомогою формули (1.15а), позаяк потенціал поля однієї кульки φ1 складає половину заданого сумарного потенціалу φ:
$k\frac{q}{l}=\frac{\varphi }{2}$ $\Rightarrow $ ${{E}_{1}}=\frac{\varphi }{2l}$.
Відтак, підставивши це значення у вираз (2), отримаємо остаточну відповідь
$E=\frac{\varphi }{l}\cdot \frac{\sqrt{3}}{2}$ = 86,6 В/м.
Задача 1.6 У вершинах правильного трикутника зі стороною a = 10 см закріплено точкові заряди q1 = 1 нКл, q2 = –2q1 і q3 = –3q1.
Визначити
напруженість \(\vec{E}_{0}\) електричного поля в центрі трикутника.
|
Дано:
a = 10 см = 0,1 м
q1= 1 нКл = 10-9 Кл
q2= –2q1 = –2·10-9 Кл
q3= –3q1 = –3·10-9 Кл
|
| \(\vec{E}_{0}\) – ? |
Розв'язання
За принципом суперпозиції шуканий вектор
|
|
\(\vec{E}_{0}=\vec{E}_{1}+\vec{E}_{2}+\vec{E}_{3}\), |
(1) |
де \(\vec{E}_{1}\), \(\vec{E}_{2}\), \(\vec{E}_{3}\) – напруженості полів кожного із зарядів у точці O, рис. 6. Характеристиками шуканого вектора \(\vec{E}_{0}\) є його модуль Е та кут α, між ним і віссю ОХ. Для визначення цих величин оберемо систему вектора координат XOY, як показано на рис. 6, і запишемо рівняння (1) для проєкцій вектора \(\vec{E}_{0}\), враховуючи величину кутів між складовими векторами й осями та знаки проєкцій:
|
OX: \(E_{x}=(E_{1}+E_{2})\cos{30}^{\circ}\); OY: \(E_{y}=(E_{1}-E_{2})\sin{30}^{\circ}+E_{3}\). |
(2) |
 |
Звідси за допомогою формули (1.6а) можна визначити проєкції складових векторів і параметри результуючого вектора \(\vec{E}_{0}\). Але, враховуючи, що величини зарядів відносяться як (1 : 2 : 3) і відстань від них до т О \(r=a/2\cos{30}^{\circ}=a/\sqrt{3}\), рівняння (2) задля зручності спочатку варто записати у вигляді
Ex = 3ηcos30°;
Ey = η(3 – sin30°), де η =(3kq1/a2) = 2700 В/м,
і відтак обчислити проєкції Ex = 7015 В/м, Ey = 6750 В/м й остаточну відповідь:
\(E=\sqrt{E_{x}^{2}+E_{y}^{2}}=9735\) В/м;
\(\mathrm{tg}\alpha=\frac{E_{y}}{E_{x}}=0,962\) \(\Rightarrow \) \(\alpha=\) 43,9°.
Побудований за знайденими проєкціями вектор \(\vec{E}_{0}\) показано на рис. 6.
Задача 1.7
Точкові заряди q і –q розташовано на осі OX на відстані 2l один від одного.
Визначити та показати
на графіку залежність Ex(x) проєкції напруженості електричного поля зарядів на лінії їхнього розташування.
|
Дано: q, –q, l
|
|
Ex(x) – ?
|
Розв'язання
За принципом суперпозиції (1.7) у будь-якій точці напруженість поля системи \(\vec{E}\) дорівнює сумі напруженостей \(\vec{E}_{1}\), \(\vec{E}_{2}\) поля кожного із зарядів q1 = q і q2 = –q. Це стосується й проєкцій:
|
\(\vec{E}=\vec{E}_{1}+\vec{E}_{2}\) → Ех = Е1х + Е2х. |
(1) |
Зважаючи на співвідношення між модулями й напрямками (тож і знаками проєкцій) векторів складових і результуючого полів, лінія розташування зарядів (рис.7а) поділяється на три області А, В і С, із характерним для кожної співвідношенням між напрямками складових полів і величинами їхньої напруженості. Позаяк за умовою вектори \(\vec{E}_{1}\), \(\vec{E}_{2}\) і \(\vec{E}\) лежать на осі ОХ,
проєкції полів зарядів залежно від області складають Е1х = ± Е1 і Е2х = ± Е2, а для результуючого поля в кожній області визначаються виразами:
|
– Область А ( x < 0): Е1 > Е2 → Ех = – (Е1 – Е2) < 0. – Область В ( –l < x < l): Е1х, Е2х > 0 → Ех = Е1 + Е2 > 0. – Область С (x > l): Е1 < Е2, → Ех = – (Е2 – Е1) < 0. |
(2) |
При цьому в кожній точці з координатою х величини Е1 і Е2 визначаються відстанями r1 і r2 від неї до зарядів, які складають:
|
– Область А ( x < 0): r1 = |x| – l, r2 = |x| + l. – Область В ( –l < x < l): r1 = l – |x|, r2 = l + |x|, або r1 = l + |x|, r2 = l – |x|. – Область С (x > l): r1 = x + l r2 = x – l. |
(3) |
Відтак, підставивши записані вирази r1 і r2 у формулу (1.6а), знайдемо модулі E1 і E2, а потім за співвідношеннями (2) після перетворень отримаємо наступні вирази проєкцій Ex (x) для результуючого поля:
|
– Область А : $E=-4kql\frac{\left| x \right|}{\left( {{x}^{2}}-{{l}^{2}} \right)}$. – Область В : $E= 2kl\frac{{{x}^{2}}+{{l}^{2}}}{{{\left( {{x}^{2}}-{{l}^{2}} \right)}^{2}}}$. – Область С : $E=-4kql\frac{\left| x \right|}{\left( {{x}^{2}}-{{l}^{2}} \right)}$. |
(4) |
Далі слід було би побудувати за розрахунковими точками графік залежності Ex (x). Але його вигляд можна встановити й без розрахунків, опираючись на наступні міркування.
1. У кожній точці переважає поле заряду, що розташований ближче. Тож, як видно з рис.7а, в областях А і С проєкція результуючого поля Ех < 0, а в області В Ех > 0..
2. З тієї ж причини в усіх областях величина |Ех| зменшується при віддаленні від ближнього заряду.
3. За умовою |q2| = q1, тому графіки складових і результуючого полів є симетричним відносно осі ординат.
З урахуванням наведених міркувань графік Ex (x) виглядає, як показано на рис. 7б.
Задача 1.8.
Електричне поле створюється металевою кулею радіуса R1 = 1 см із зарядом q = 1 нКл, до якої щільно прилягає сферичний шар діелектрика з проникністю \(\varepsilon=4,5\) і зовнішнім радіусом R2 = 2 см.
Визначити та показати на графіках
залежності напруженості E(r) і потенціалу φ(r) поля кулі від відстані r до її центра.
|
Дано: R1 = 1 см = 0,01 м
R2 = 2 см = 0,02 м
q = 1 нКл = 10–9 Кл
\(\varepsilon=4,5\)
|
|
E(r) –?
\(\varphi(r)\) –?
|
Розв'язання
Для початку згадаємо деякі загальні відомості з теорії (п. 1.1).
1. Заряд q є рівномірно розподілений по поверхні кулі й створює електричне поле лише назовні.
2. Під дією поля кулі діелектрик поляризується: електрони в атомах трохи зміщуються в напрямі центра шару, й на його поверхнях з’являються поляризаційні (”зв’язані“) заряди однакової величини – q′ і +q′ (рис. 8). Ці заряди на додачу до поля зарядів кулі \(\vec{E}_{k}\) створюють зустрічне внутрішнє поле ${\vec{E}}'$, яке зменшує результуючу напруженість до величини (формула (1.6а))
${{E}}=\frac{{{{{E}}}_{k}}}{\varepsilon }$.
3. За умовою діелектрик є однорідним (ε = const) і в об’ємі лишається електрично нейтральним. Отож досліджуване електричне поле створюється двома рівномірно зарядженими концентричними сферами радіуса R1 і R2, які поділяють весь простір на три області: А (провідник, r < R1), В (діелектрик, R1 ≤ r < R2) і С (вільний простір, r ≥ R2), напруженість і потенціал поля в кожній з яких треба визначати окремо.

Напруженість Е(r)
Область А (r < R1). У провіднику електростатичне поле існувати не може, тож усередині кулі скрізь, включно з точками r = R1,
ЕА(r) = 0.
Область В (R1 ≤ r ≤ R2). У шарі діелектрика напруженість поля визначається формулою (1.6);
${{E}_{1B}}=\frac{q}{4\pi {{\varepsilon }_{0}}\varepsilon {{r}^{2}}}=\frac{kq}{\varepsilon {{r}^{2}}}$.
Відповідно, на поверхнях
${{E}_{1B}}=\frac{kq}{R_{1}^{2}}$ і ${{E}_{2B}}=\frac{kq}{R_{2}^{2}}$.
Область С (r ≥ R2). У цій області простору ε = 1, отже
${{E}_{С}}=\frac{kq}{{{r}^{2}}}$,
і в прилеглих до діелектрика точках
${{E}_{2C}}=\frac{kq}{R_{2}^{2}}$.
Таким чином, на графіку залежність Е(r) зображується відрізками квадратичних гіпербол, а на межах областей спостерігаються стрибки від Е1А = 0 до Е1B та від Е2В до Е2С, відповідно.
Потенціал φ(r)
Потенціал поля назовні рівномірно зарядженої сферичної поверхні, як і напруженість, збігається з такою для точкового заряду (формула (1.18)). Але позаяк потенціал визначається не напруженістю як такою, швидкістю її зміни, то відсутність поля (E(r) = 0) в якійсь частини польової зони означає не нульову величину, а сталість потенціалу (φ = const). Тому на графіку φ(r) не може бути стрибків (розривів).
Шукану залежність φ(r) будемо аналізувати в зворотньому порядку, рухаючися від віддаленої точки до центра кулі.
Область С (r ≥ R2). Ця область є вільна від діелектрика (для повітря ε = 1), отже за формулою (18а)
${{\varphi }_{C}}\left( r \right)=\frac{kq}{r}$,
і на прилеглій до діелектрика поверхні (r =R2)
${{\varphi }_{2}}=\frac{kq}{{{R}_{2}}}$.
Область В (R1 ≤ r ≤ R2). У діелектрику в напрямі до центра (при зменшенні r) потенціал продовжує зростати, починаючи з величини φ2. Тому φB = φ2 + ΔφВ, де ΔφВ – зміна потенціалу на шляху від т. 2 (зовнішня поверхня діелектрика) до довільної точки на відстані r від центра. Отже, згідно з формулою (1.18а),
${{\varphi }_{B}}={{\varphi }_{2}}+\frac{kq}{\varepsilon }\left( \frac{1}{r}-\frac{1}{{{R}_{2}}} \right)$,
і в т. 1 (r =R1)
\({{\varphi }_{1}}={{\varphi }_{2}}+\frac{kq}{\varepsilon }\left( \frac{1}{{{R}_{1}}}-\frac{1}{{{R}_{2}}} \right)\).
Область А (r < R1). Всередині кулі E = 0, і потенціал лишається сталим і складає
φА = φ1.
Далі належало би за за отриманими виразами та даними умови розрахувати таблиці значень і побудувати графіки залежностей E(r) і φ(r). Але в цьому немає потреби, бо їхній загальний вигляд є очевидним. А саме, області А вони зображуються горизонтальними відрізками, а в кожній з областей В і С – відрізками гіпербол. Тож для повного відображення картини поля достатньо за отриманими формулами обчислити його характеристики в точках 1 і 2:
Е1 = 0 і 20 кВ; Е2 = 5 кВ і 22,5 кВ;
φ1 = 550 В; φ2 =450 В.
Вигляд графіків залежностей E(r) і φ(r) показано на рис. 8-1.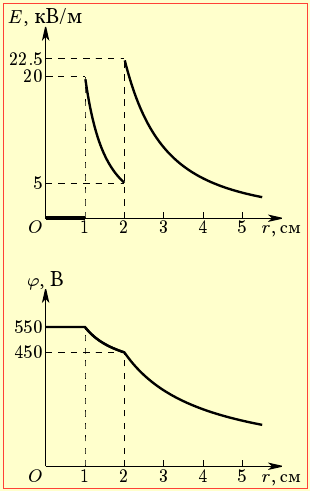 Рис. 8-1
Рис. 8-1
Задача 1.9
Дві паралельні пластини із густиною заряду σ1 і σ2 закріплено перпендикулярно до осі ОХ у точках x = 0 і х = d (рис. 9). Уважаючи електричне поле системи однорідним,
визначити та показати на графіку
залежність від координати x: А) проєкції напруженості Ех(х); Б) потенціалу φ(х), прийнявши φ(0) = 0. Розглянути випадки: 1. σ1 = σ, σ2 = 2σ; 2. σ1 = σ, σ2 = – σ.
|
Дано: d, σ
|
|
Ех(х) – ?
φ(x) – ?
|
Розв'язання
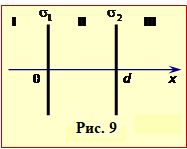
Заряджені пластини поділяють весь простір на три області: I, II, III (рис. 9), в яких за принципом суперпозиції (вирази (1.7), (1.15)) напруженість і потенціал електричного поля системи дорівнює сумі цих характеристик для поля кожної з пластин:
|
|
${{E}_{x}}={{E}_{1x}}+{{E}_{2x}}$ $\varphi ={{\varphi }_{1}}+{{\varphi }_{2}}$ |
(1) (2) |
При цьому напруженість визначаються заданою величиною σ (формула (1.9)), а потенціал – ще й вибором нульового рівня (п. 1.3). Тож надалі задля зручності введемо позначення (σ/2ε0) = E0 й за нульову точку потенціалу приймемо ліву пластину: φ(0) = 0.
Випадок 1.
А) У цьому випадку вектори \(\vec{E}_{1}\) і \(\vec{E}_{2}\), згідно з прийнятим позначенням і формулою (1.9), мають модулі Е1 = Е0, Е2 = 2Е0 і спрямовані, як на рис. 9-1а. Отже, для поля кожної пластини та системи в цілому маємо по областях:
|
І (х < 0) ІІ (0 < х < d) ІІІ (х > d) |
E1х = – Е0, Е2х = – 2Е0 $\Rightarrow$ ЕІх = – 3Е0 E1х = Е0, Е2х = – 2Е0 $\Rightarrow$ ЕІІх = –Е0 E1х = Е0, Е2х = 2Е0 $\Rightarrow$ ЕІІІх = 3Е0 |
(1A) |
${{E}_{x}}=-\frac{\varphi \left( x \right)}{x}$ $\Rightarrow$ $\varphi \left(x \right)=-\frac{{{E}_{x}}}{x}$
Аналогічно, прийнявши x1 = d, отримаємо для зони ІІІ:
${{E}_{x}}=-\frac{\varphi \left( x \right)-\varphi \left( d \right)}{x-d}$ $\Rightarrow$ $\varphi \left( x \right)=-{{E}_{x}}\left( x-d \right)+\varphi \left( d \right)$
Відтак, урахувавши дані таб. (1А), отримуємо наступні відповіді:
|
І (х < 0) ІІ (0 < х < d) ІІІ (х > d) |
$\varphi \left( x \right)= {{3E}_{0}}x$ $\varphi \left( x \right)= {{E}_{0}}x$ $\varphi \left( x \right)={{E}_{0}}\left( 4d-3x \right)$ |
(1Б) |
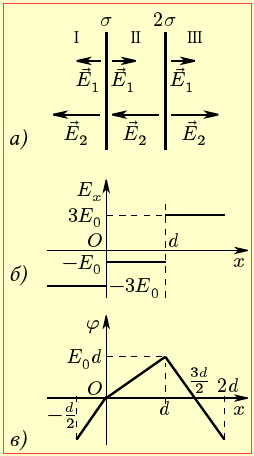
Таким чином, потенціал у напрямку осі ОХ в областях І, ІІ лінійно зростає, а в області ІІІ лінійно спадає. Відтак для побудови графіка (рис. 9-1в ) розрахуємо через величину E0 = (σ/2ε0) значення φ(x) у наступних точкахx
| х |
-d/3 |
0 |
d |
4d/3 |
5d/3 |
|
φ |
-E0d |
0 |
3E0d |
0 |
-E0d |
Випадок 2.
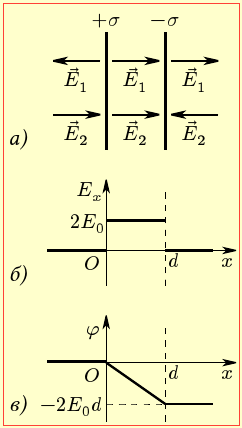
У цьому випадку \(\sigma_{1}\) = –\(\sigma_{2}\), і складові вектори \(\vec{E}_{1}\), \(\vec{E}_{2}\) мають однакові модулі та показані на рис. 9-2а напрямки.
Тож, згідно із співвідношенням (1), величина Ex в областях І, ІІІ дорівнює 0, а в області ІІІ складає 2Е0, як показано на рис. 9.2б. Відповідно, в області ІІ потенціал у напрямку осі OХ лінійно спадає від прийнятого значення φ(0) = 0 до φ(d) = –2Е0d, а поза нею лишається сталим (рис. 9.2в).
Варто зазначити, що цей випадок є характерним для плоского конденсатора, тож отриманий результат заслуговує на окрему увагу.
Задача 1.10.
По розміщеному в повітрі тонкому кільцю радіуса R рівномірно розподілено заряд q.
Визначити:
А) напруженість електричного поля Е на осі кільця в залежності від відстані r до його центра;
Б) проаналізувати залежність Е(r) і показати загальний вигляд її графіка.
|
Дано: R, q |
|
E(r) - ? |
Розв'язання
А). За принципом суперпозиції (1.7) напруженість $\vec{E}$ електричного поля кільця в будь-якій точці простору дорівнює сумі напруженостей полів його частин. Отож, подумки розділивши кільце на однакові малі ділянки й розклавши напруженість кожної на паралельну ${{\vec{E}}_ {i\parallel }}$ та перпендикулярну ${{\vec{E}}_{i\bot }}$ до осі кільця складову, можна записати
| $\vec{E}$ = $\sum{{{{\vec{E}}}_{i\parallel }}}$ + $\sum{{{{\vec{E}}}_{i\bot }}}$. | (1) |
У цьому виразі модулі та напрямки складових векторів визначаються формулою (1.6) через відстані та розташування заданої точки поля відносно всіх точок кільця. Тому розв'язати задачу в загальному вигляді (знайти формулу) для довільної точки не можна. Але на осі перпендикулярні складові полів діаметральних ділянок і всього кільця є компенсовані:
$\sum{{{{\vec{E}}}_{i\bot }}}$ = 0.
Тож, результуюча напруженість
$\vec{E}$ = $\sum{{{{\vec{E}}}_{i\parallel }}}$
є спрямована вздовж осі кільця й відповідно до формули (1.6) має модуль
$E=\sum{\left( \frac{\Delta {{q}_{i}}}{4\pi {{\varepsilon }_{0}}r_{i}^{2}}\cos {{\alpha }_{i}} \right)}$
Відтак, урахувавши, що за умовою відстані rі , отже й кути ${{\alpha }_{i}}$, є однакові й складають
${{r}_{i}}=\sqrt{{{r}^{2}}+{{R}^{2}}}$ і $\cos {{\alpha }_{i}}=\frac{r}{\sqrt{{{r}^{2}}+{{R}^{2}}}}$
отримаємо наступну відповідь:
| $E=\frac{qr}{4\pi {{\varepsilon }_{0}}\sqrt{{{\left( {{r}^{2}}+{{R}^{2}} \right)}^{3}}}}$ | (1) |
Б). Аби скласти наочне уявлення про характер залежності Е(r) на осі кільця, запишемо її наближені вирази поблизу ($r\ll R$) та далеко ($r\gg R$) від центра, де величиною r, або R можна нехтувати. А саме,
$r\ll R$ : $E\left( r \right)\approx \frac{qr}{4\pi {{\varepsilon }_{0}}{{R}^{3}}}$;
$r\gg R$ : $E\left( r \right)\approx \frac{q}{4\pi {{\varepsilon }_{0}}{{r}^{2}}}$
Із записаних виразів випливає, що при віддаленні від центра кільця напруженість поля спочатку лінійно, а потім уповільнено зростає так, що на певній відстані rm сягає максимуму і далі монотонно спадає, як показано на рис. 1.10-2.
З приводу отриманої залежності Е(r) (вираз ) варто зробити два зауваження.
1. Узявши та прирівнявши до нуля похідну Е′(r) від виразу (1), можна показати, що ${{r}_{m}}=\frac{R}{\sqrt{2}}$;
2. При $r\gg R$ значення Е(r) наближаються до величини напруженості поля точкового заряду (формула (1.6)). Це є цілком зрозумілим, позаяк кільце, як також і будь-які інші тіла, з великої відстані виглядають, як точкові.
Задача 1.11. Два однакові точкові заряди +q і –q, що закріплені на невеликій відстані l один від одного (рис. 11), утворюють "електричний диполь".
Установити
вираз залежності його потенціалу \(\varphi \left(r,\vartheta \right)\) в повітрі від відстані до центра r і кута (\vartheta \) за умови \(r\gg l\).
|
Дано: q, l, r, |
|
$\varphi (r,\vartheta )$ -? |
Розв'язання
Відповідно до принципу суперпозиції (вираз (1.15)) шуканий потенціал
$\varphi ={{\varphi }_{+}}+{{\varphi }_{-}}$
де φ+ і φ– – потенціали полів окремих зарядів ("полюсів") у повітрі визначаються формулою (1.16) при ε = 1, в якій через малість величини $l$ відстані до заданої точки до полюсів (див. рис. 11) складають \({{r}_{+}}=l-\Delta r\) і \({{r}_{-}}=l+\Delta r\), а \(\Delta r=\left( l/2 \right)\cos \vartheta\). Отже,
$\varphi =\frac{q}{4\pi {{\varepsilon }_{0}}}\left( \frac{1}{r-\left( l/2 \right)\cos \vartheta }-\frac{1}{r+\left( l/2 \right)\cos \vartheta } \right)$ $\Rightarrow $
$\varphi =\frac{ql\cos \vartheta }{{{r}^{2}}-{{\left( l/2 \right)}^{2}}{{\cos }^{2}}\vartheta }$
Позаяк за умовою \(r\gg{l}\), в записаному виразі величина ${{\left( l/2 \right)}^{2}}{{\cos }^{2}}\vartheta $ є неістотною, тож маємо наступну кінцеву віповідь:
\(\varphi =\frac{ql}{4\pi {{r}^{2}}}\cos \vartheta \) (\(r\gg l\))
Провідники. Конденсатори
Задача 1.12. Металева куля радіусом R = 6 см має заряд q = 1 нКл. Визначити напруженість E і потенціал φ електричного поля кулі на відстані a = (R/3) від поверхні.
Задача 1.13. Вісім заряджених малих крапельок ртуті з потенціалом \(\varphi_{1}\) = 1В кожна злилися в одну. Визначити потенціал \(\varphi\) краплі, що утворилась.
Задача 1.14. Заряджену до потенціалу φ0 = 100 В металеву кульку радіуса r з'єднали тонким провідником з незарядженою сферичною провідною оболонкою радіуса R0 = nr, де n = 4. Визначити, яким став потенціал φ кульки після з'єднання, якщо вона є розташована: а) далеко від оболонки і б) всередині неї без дотику.
Задача 1.15. Заряджену до потенціалу φ = 30 В металеву кулю радіуса R = 1 см концентрично розмістили всередині незарядженої провідної оболонки радіусом R0 = 3 см, котру по тому заземлили. Визначити, яким став потенціал кулі φ1.
Задача 1.16. Плоский конденсатор із площею обкладки S заповнено двома паралельними до них шарами діелектрика з проникностями ε1, ε2 і товщинами d1, d2, відповідно. Визначити ємність конденсатора.
Задача 1.17. У зазор між обкладками зарядженого плоского конденсатора ввели пластину діелектрика з проникністю ε = 5 і товщиною в n = 3 рази меншою за відстань між обкладками. Визначити у скільки разів змінилася напруга на конденсаторі.
Задача 1.18. Три конденсатори C1 = 2 мкФ, C2 = 1 мкФ, C3 = 5 мкФ з'єднан0, як на рис.18. Визначити: 1. Загальну ємність з'єднання С0; 2. Заряди qi і напруги Ui на окремих конденсаторах при напрузі на з'єднанні U0 = 20 В.
Задача 1.19. Два заряджені від одного джерела конденсатори ємністю C1 = 10 мкФ і C2 = 2 мкФ з’єднали різнойменними обкладками. Визначити, у скільки разів змінилася напруга на конденсаторах.
Задача 1.20. Визначити різницю потенціалів U між точками d і e у схемі рис.20, якщо між точками a і b напруга U0 = 10 В. Ємності конденсаторів: C1 = 1 мкФ, С2 = 4 мкФ, С3 = 2 мкФ, С4 = 3 мкФ.
Задача 1.12
Металева куля радіусом R = 6 см має заряд q = 1 нКл.
Визначити
Напруженість E і потенціал φ електричного поля кулі на відстані a = (R0/3) від поверхні.
|
Дано: R = 6 см = 10–2 см q = 1 нКл = 10–9 Кл a = (R0/3) |
|
Е - ?; φ - ? |
Розв'язання
Умову задачі задовольняють точки, розташовані від центра кулі на відстанях r1 = R0 + a (випадок 1.) та r2 = R0 – a (випадок 2.).
1. Назовні напруженість Е і потенціал φ поля кулі збігаються з такими для точкового заряду q, розміщеного в її центрі (п. 1.5), й визначаються формулами (10.6a) і (10.15a). Отже, враховуючи, що для повітря ε = 1 і відповідно до умови r = (4R0/3), знаходимо:
\(E_{1}=\frac{9kq}{16R^{2}}\); φ1 = \(\frac{3kq}{4R}\),
де \({k}=1/4\pi\varepsilon_{0}=9\cdot{10}^{9}\) м/Ф.
У числах:
Е1 ≈ 1,4·103 В = 1,4 кВ, φ1 = 112,5 В.
2. Всередині провідника E = 0 (п. 1.5), тож потенціал φ2 є сталим і рівним потенціалові її поверхні, що визначається формулою (1.15а) при r = R. Отже,
E2 = 0; \(\varphi_{2}=\frac{kq}{R}\) = 150 В.
Задача 1.13
Вісім заряджених малих крапельок ртуті з потенціалом \(\varphi\) = 1В кожна злилися в одну.
Визначити
потенціал \(\varphi_{0}\), краплі, що утворилась.
|
Дано: n = 8 \(\varphi\) = 1 В |
|
\(\varphi_{0}\) - ? |
Розв'язання
Через великий поверхневий натяг ([ІІ], п. 3.1) ртуті та малі розміри крапель їх можна вважати кульками й згідно з формулою (1.18) записати:
|
$\frac{{{\varphi }_{0}}}{\varphi }=\frac{{{q}_{0}}}{q}\cdot \frac{r}{{{r}_{0}}}$, |
(1) |
де q0, q і r0, r – заряди й радіуси утвореної краплі та вихідних крапельок, відповідно. За умовою відношення зарядів
$\frac{{{q}_{0}}}{q}=n$.
Таким самим є й відношення відповідних об'ємів, отже, відношення радіусів складає
$\frac{r}{{{r}_{0}}}=\sqrt[3]{\frac{V}{{{V}_{0}}}}=\frac{1}{\sqrt[3]{n}}$.
Відтак із співвідношення (1) дістаємо відповідь:
${{\varphi }_{0}}=\frac{\varphi }{\sqrt[3]{{{n}^{2}}}}$ = 4В.
Задача 1.14
Заряджену до потенціалу \(\varphi_{0}\) = 100 В металеву кульку радіуса r з'єднують довгим тонким провідником з незарядженою сферичною провідною оболонкою радіуса R = nr, де n = 4.
Визначити,
яким став потенціал φ кульки після з'єднання, якщо вона є розташована:
а) далеко від оболонки і
б) всередині неї без дотику.
|
Дано: φ0 = 100 В
R = nr
n = 4
|
| φ - ? |
Розв'язання
а) Через велику відстань між кулькою й оболонкою можна не враховувати взаємодію між ними й обчислювати потенціал за формулою (1.16). Крім того, через малу товщину провідника можна вважати не істотним заряд, який осідає на ньому з'єднуванні тіл.
Умовою рівноваги зарядів у провідниках є їхня еквіпотенціальність (п. 1.5). Тому після з'єднання оболонка буде заряджатися, доки її потенціал не зрівняється з потенціалом кульки. Отже, відповідно до формули (1.16а),
|
$\frac{q}{r}=\frac{{{q}'}}{R}$, |
|
де q′ = (q0 – q) – заряд оболонки, котрий дорівнює різниці початкового та кінцевого заряду кульки. Відтак,
$q=\frac{{{q}_{0}}r}{R+r}$.
Тож, урахувавши умову R = nr, дістанемо:
$q=\frac{{{q}_{0}}}{n+1}$,
і
\(\varphi=\frac{\varphi_{0}}{n+1}\) = 20 В.
б) Як і раніше, при з'єднанні тіла набудуть однакового потенціалу φ, але в цьому випадку весь заряд кулі q0 перейде на зовнішню поверхню оболонки. Отже,
$\varphi =\frac{k{{q}_{0}}}{R}$
і, враховуючи умову R =nr та вираз (1.16а),
$\varphi =\frac{{{\varphi }_{0}}}{n}=25$В.
Задача 1.15
Заряджену до потенціалу φ = 30 В металеву кулю радіуса R = 1 см концентрично розмістили всередині незарядженої провідної оболонки радіусом R0 = 3 см, котру по тому заземлили.
Визначити,
яким став потенціал кулі φ1.
|
Дано: φ = 30 В
R = 1 см = 10–2 м
Rо = 3 см = 3·10–2 м
|
| φ2 - ? |
Розв'язання
Відповідь даної задачі можна дістати двома способами.
І спосіб ґрунтується на наступних положеннях електростатики провідників (пп. 1.2 – 1.5). 1. У провідниках увесь надлишковий заряд розміщується на зовнішній поверхні. 2. Напруженість поля всередині зарядженого провідника дорівнює нулю, а потенціал є однаковий і рівний потенціалові поверхні. 3. Електростатичне поле зарядженої провідної кулі, або кульового шару (оболонки), збігається з полем розташованого в центрі такого самого точкового заряду.
При вміщенні зарядженої кулі якимось, приміром позитивним, зарядом q всередину незаземленої оболонки частина її вільних електронів виходить на внутрішню поверхню, створюючи на ній "індукований" заряд $q_{i}^{-}$, а на зовнішній, відповідно, з'являється такий самий позитивний заряд $q_{i}^{+}$, як схематично показано на рис. 15а.

Таким чином, маємо систему з трьох концентричних заряджених сфер, навколо яких створюються власні (складові) електричні поля, що за принципом суперпозиції (п. 1.2) формують загальне (результуюче) поле.
Як говорилося, вказані поля є такими, ніби відповідні заряди знаходяться в центрі кулі. Тож напруженість результуючого поля на заданій відстані r від центра визначається формулою (1.6), в якій $q$ є сумою заряду кулі та індукованого заряду оболонки всередині сфери радіуса r. Зокрема, для області між кулею та оболонкою (R ≤ r ≤ R0) поле створюється лише зарядом кулі, котрий за умовою та формулою (1.18) дорівнює
|
\(q=4\pi {{\varepsilon }_{0}}R\varphi \). |
(1) |
У самій провідній оболонці результуюча напруженість складається з напруженостей полів заряду кулі $q$ та індукованого заряду внутрішньої поверхні оболонки $q_{i}^{-}$ й дорівнює нулю, отже,
| q – qi = 0 $ \Rightarrow $ qi = q. | (2) |
Рівність (2) означає, що по модулю інуковані заряди збігаються із зарядом кулі. Через це результуюча напруженість поля назовні оболонки (r > R0), хоча формально залежить від усіх зарядів $q$, $q_{i}^{-}$ і $q_{i}^{+}$, реально, як і в порожнині, визначається тільки зарядом кулі $q$.Таким чином,
незаземлена провідна оболонка ніяк не впливає на електричне поле в навколишньому просторі.
Але при заземленні ситуація суттєво змінюється, позаяк індукований заряд $q_{i}^{+}$ стікає, й оболонка набуває заряду $q_{i}^{-}$. Через це в самій оболонці та назовні створюється власне поле, що спрямоване протилежно до поля кулі й завдяки співвідношенню (2) рівне йому по модулю, тож заземлена провідна оболонка повністю компенсує (екранує) електричне поле вміщеної всередину зарядженої кулі. До слова,
в теорії доводиться, що вказаний ефект має місце незалежно від форми оболонки та форми й розташування вміщеного в неї тіла).
Напруженість поля всередині провідної оболонки як до, так і після заземлення лишається нульовою. Але цього не можна сказати про потенціал, бо напруженість визначає не сам потенціал, а швидкість його зміни при переміщенні вздовж напряму поля (див. п. 1.4). Тож нульова напруженість у деякій області простору означає не нульове значення потенціалу, а тільки те, що його величина є сталою. Тому після заземлення оболонки всередині скрізь, включно з кулею, до потенціалу поля кулі додається ще й потенціал оболонки, що стала зарядженою:
\(\varphi_{1}=\varphi+\varphi_{о}\).
Отож, враховуючи вираз (1), за формулою (1.18) отримуємо потенціал оболонки
\(\varphi_о=-\varphi\frac{R}{R_о}\)
та наступну кінцеву відповідь задачі:
\(\varphi_{1}=\varphi\left(1-\frac{R}{R_{о}}\right)\) = 20 В.
ІІ спосіб. Будемо розглядати кулю як внутрішню обкладку зарядженого сферичного конденсатора із зовнішньою обкладкою – оболонкою. Якщо так, то через заземлення оболонки напруга U на цьому конденсаторі збігається з потенціалом кулі й за виразом (1.23) складає
\({{\varphi }_{1}}=\frac{q}{C}\).
Звідси, врахувавши вирази (1) для q та (1.27) для С, дістанемо відповідь:
\(\varphi_{1}=\varphi\left(1-\frac{R}{R_{о}}\right)\) = 20 В,
що, природньо, збігається з отриманою раніше.
Задача 1.16
Плоский конденсатор із площею обкладки S заповнено двома паралельними до них шарами діелектрика з проникностями ε1, ε2 та товщинами d1, d2, відповідно (рис. 16).
Визначити
ємність конденсатора.
|
Дано: S
ε1, ε2
d1, d2
|
| C - ? |
Розв'язання
Задачу можна розв'язати в два способи.
I. За означенням (1.23) ємність конденсатора дорівнює
|
$C=\frac{q}{{U}}$ |
(1) |
Отже, для отримання відповіді необхідно визначити напругу на конденсаторі з двошаровим діелектриком при заданому заряді на обкладках, що на загал є складним завданням. Але в даній задачі воно спрощується через однорідність електричного поля в плоскому конденсаторі (див. п. 1.5).
Напруга U на обкладках заданого конденсатора дорівнює сумі напруг U1 і U2 на шарах діелектрика, які визначаються напруженостями поля через співвідношення (1.20):
$U={{U}_{1}}+{{U}_{2}}={{E}_{1}}{{d}_{1}}+{{E}_{2}}{{d}_{2}}$.
При цьому величина Е в кожному шарі виражається формулою (1.25):
$E=\frac{q}{{{\varepsilon }_{0}}\varepsilon S}$,
отже,
|
$U=\frac{q}{{{\varepsilon }_{0}}S}\left( \frac{{{d}_{1}}}{{{\varepsilon }_{1}}}+\frac{{{d}_{2}}}{{{\varepsilon }_{2}}} \right)$ |
(2) |
Відтак, підставивши вираз (2) у формулу (1), дістанемо відповідь:
| $C=\frac{{{\varepsilon }_{0}}S}{\left( {{d}_{1}}/{{\varepsilon }_{1}} \right)+\left( {{d}_{2}}/{{\varepsilon }_{2}} \right)}$. |
II. Уявімо, що шари діелектрика в конденсаторі відділено один від одного дуже тонкою металевою пластиною. В такому разі при зарядці конденсатора на її поверхні вийдуть протилежні за знаком індуковані заряди однакової з обкладками величини, котрі ніяк не впливають на поле, тож і на ємність конденсатора. Але така удавана пластина дозволяє трактувати заданий двошаровий конденсатор як послідовне з'єднання двох простих конденсаторів із ємностями
| \(C^{\prime}=\frac{\varepsilon_{0}\varepsilon_{1}S}{d_{1}}\) та \(C^{\prime\prime}=\frac{\varepsilon_{0}\varepsilon_{2}S}{d_{2}}\). |
Тож, підставивши ці вирази у формулу (1.28б), після спрощень дістанемо відповідь:
\(\frac{1}{C}=\frac{1}{\varepsilon_{0}S}\left(\frac{d_{1}}{\varepsilon_{1}}+ \frac{d_{2}}{\varepsilon_{2}}\right)\) \(\Rightarrow\) $C=\frac{{{\varepsilon }_{0}}S}{\left( {{d}_{1}}/{{\varepsilon }_{1}} \right)+\left( {{d}_{2}}/{{\varepsilon }_{2}} \right)}$.
Задача 1.17
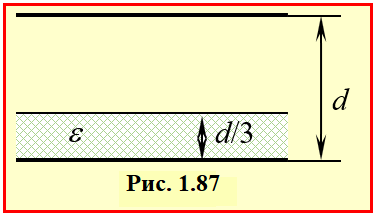
У зазор між обкладками зарядженого плоского конденсатора ввели пластину діелектрика з проникністю ε = 5 і товщиною в n = 3 рази меншою за відстань між обкладками (рис.17).
Визначити,
у скільки разів змінилася напруга на конденсаторі.
|
Дано: ε = 5
n = 3С1 = 1000 пФ
|
| U2/U1 - ? |
Розв'язання
Внаслідок уведення діелектрика ємність конденсатора змінюється від|
\(C_{1}U_{1}=C_{2}U_{2}\) \(\Rightarrow\) \(\frac{U_{2}}{U_{2}}=\frac{C_{1}}{C_{2}}\). |
(1) |
Таким чином, задача зводиться до визначення величини С2.
Початкова ємність С1 – це ємність плоского повітряного (\(\varepsilon=1\)) конденсатора, що визначається площею пластин і відстанню між ними за формулою (1.26):
\(C_{1}=\frac{\varepsilon_{0}S}{d}\),
а для визначення кінцевої ємності можна скористатися результатом задачі 1.16. Відтак, врахувавши умови \(\varepsilon_{1}=1\) та d2 = d/n, d1 = d – d2 = d(n - 1)/n і формулу (1.26), після елементарних перетворень дістанемо:\(C_{2}=C_{1}\frac{\varepsilon{n}}{\varepsilon{(n-1)}+1}\) \(\Rightarrow\) \(\frac{U_{2}}{U_{1}}=\frac{\varepsilon{(n-1)}+1}{\varepsilon{n}}\) ≈ 0,73.Таким чином, напруга на конденсаторі зменшилася приблизно в 1, 4 раза.
Зауваження. При розв'язанні задачі вважалося, що пластина діелектрика щільно прилягає до обкладки конденсатора. Але це не є необхідним. Рекомендуємо довести це самостійно.
Задача 1.18
 Три конденсатори C1 = 2 мкФ, C2 = 1 мкФ, C3 = 5 мкФ з'єднано, як на рис.18.
Три конденсатори C1 = 2 мкФ, C2 = 1 мкФ, C3 = 5 мкФ з'єднано, як на рис.18.
Визначити:
1. Загальну ємність С0 з'єднання;
2. Заряди qі і напруги Uі на окремих конденсаторах при напрузі на з'єднанні U0 = 20 В.
|
Дано: C1 = 2 мкФ
C2 = 1 мкФ
C3 = 5 мкФ
U0 = 20 В
|
|
С0-?, qі-?, Uі-?
|
Розв'язання
 1. У схемі рис.18 з'єднані паралельно конденсатори С2 і С3 за формулою (10.29) можна замінити одним еквівалентним конденсатором ємністю
1. У схемі рис.18 з'єднані паралельно конденсатори С2 і С3 за формулою (10.29) можна замінити одним еквівалентним конденсатором ємністю
С23 = С2 + С3 = 6 мкФ
як показано на рис. 18-1. Отримана еквівалентна схема являє собою послідовне з'єднання конденсаторів С1 і С23, тож шукана величина С0 за формулою (1.28б) дорівнює:
${{C}_{0}}=\frac{{{C}_{1}}{{C}_{23}}}{{{C}_{1}}+{{C}_{23}}}$ = 1,5 мкФ
2. При послідовному з'єднанні заряди кожного з конденсаторів і з'єднання в цілому є однакові (див. п. 1.5). Тому заряди на конденсаторах С1 і С23 збігаються між собою та із зарядом еквівалентного конденсатора С0, який за формулою (1.23) та даними умови складає
q0 = С0U0 = 30 мкКл.
Таким чином, онденсатора С1 маємо:
q1 = C1U1 = 30 мкКл, U1 = 15 В.
Аналогічно знаходимо заряди паралельно з'єднаних конденсаторів С2 і С3 , на яких напруги однакові й дорівнюють U0 – U1. Отже,
U2 = 5 В, q2 = C2U2 = 5 мкКл;
U3 = 5 В, q3= C3U3 = 25 мкКл.
Задача 1.19
Два заряджені від одного джерела конденсатори ємністю C1 = 10 мкФ і C2 = 2 мкФ з’єднали різнойменними обкладками.
Визначити,
у скільки разів змінилася напруга на конденсаторах.
|
Дано: C1 = 10 мкФ
C2 = 2 мкФ |
| U2/U1 - ? |
Розв'язання

Позначимо початкову та кінцеву напруги на конденсаторах як U1 і U2. Тоді за формулою (1.23), величини (модулі) їхніх початкових q1, q2 і кінцевих Q1, Q2 зарядів складають
|
q1 = C1U1, q2 = C2U1, Q1 = C1U1, Q2 = C2U1. |
(1) |
За законом збереження алгебраїчна сума зарядів обкладок, що з’єднуються (рис. 19), лишається незмінною:
| Q1 + Q2 = |q1 – q2|, |
(2) |
Тож із урахуванням виразів (1) і (2) дістанемо:
| \((C_{1}-C_{2})U_{1}=(C_{1}+C_{2})U_{2}\) \(\Rightarrow\) \(\frac{U_{2}}{U_{1}}=\frac{C_{1}-C_{2}}{C_{1}+C_{2}}=\frac{2}{3}\). |
Таким чином, після з'єднання різнойменними обкладками напруга на конденсаторах зменшилась у півтора рази.
Задача 1.20
Визначити
різницю потенціалів U між точками d і e у схемі рис. 20, якщо між точками a і b напруга U0 = 10 В. Ємності конденсаторів: C1 = 1 мкФ, С2 = 4 мкФ, С3 = 2 мкФ, С4 = 3 мкФ.
|
Дано: C1 = 1 мкФ С2 = 4 мкФ С3 = 2 мкФ С4 = 3 мкФ U0 = 10 В |
| U - ? |
Розв'язання
Уведемо для напруг на конденсаторах позначення U1, U2, U3, U4 , а для потенціалів відповідних точок  на схемі (рис 20) — φа, φb, φd, φe, і приймемо φа > φb. Тоді
на схемі (рис 20) — φа, φb, φd, φe, і приймемо φа > φb. Тоді
φа – φd = U1 $\Rightarrow $ φd = φа – U1,
φа – φe = U3 $\Rightarrow $ φe = φа – U3.
Тож шукана напруга U = φd – φe складає U = U3 – U1, і з урахуванням формули (1.23)
|
$U=\frac{{{q}_{3}}}{{{C}_{3}}}-\frac{{{q}_{1}}}{{{C}_{1}}}$, |
|
де величини q1 і q3 є такі самі, як заряди послідовних ланцюжків C1-C2 та C3-C4, тобто
q1 = C12U0; q3 = C34U0,
де C12, C34 – ємності з'єднань.
Отже, шукана напруга складає
|
$U=\left( \frac{{{C}_{34}}}{{{C}_{3}}}-\frac{{{C}_{12}}}{{{C}_{1}}} \right){{U}_{0}}$. |
|
Відтак, виразивши ємності C12, C34 за формулою (1.28б), отримаємо наступну відповідь:
\(U=\left(\frac{C_{4}}{C_{3}+C_{4}}-\frac{C_{2}}{C_{1}+C_{2}}\right)U_{0}\).
Обчислення дають:
U = –2 В.
Знак “–” вказує на те, що φd < φe.
Робота та енергія електричного поля
У задачах цього розділу переважно розглядаються зміни електростатичної енергії при зміні заряду окремих провідників та конденсаторів. При цьому конденсатори розглядаються як пари абстрактних паралельних провідних поверхонь-обкладок, зазор між якими можна змінювати, а також подавати на них довільні за величиною й знаком заряди. Проте при зарядці за допомогою джерела напруги заряди подаються на конденсатор не іззовні, а переносяться з однієї обкладки на іншу, тож є різнойменними й однаковими за величиною.
Слід також сказати, що теоретично заряджання та перезаряджання конденсатора супроводжується електромагнітним випромінюванням, але для задач електростатики цей ефект є неістотним.
Задача 1.21. Три однакові точкові заряди q = 1 нКл розташовано у вершинах правильного трикутника зі стороною a = 20 см . Визначити роботу A, яку треба виконати, аби один із зарядів перенести на середину протилежної сторони трикутника.
Задача 1.22. Металеву кулю радіуса R = 10 см, яка містить заряд q = 100 нКл, з'єднують провідником із землею. Визначити кількість теплоти Q, що виділиться в провіднику.
Задача 1.23. Заряджений до напруги U = 100 В конденсатор C1 = 10 мкФ з'єднують із незарядженим конденсатором С2 = 5 мкФ. Визначити, яка енергія ΔW виділяється при цьому.
Задача 1.24. У зарядженому від джерела напруги повітряному конденсаторі з енергією W0 збільшують відстань між пластинами в n разів а) при відімкненому та б) при приєднаному джерелі. Визначити роботу А, що виконується в кожному випадку, та пояснити, за рахунок чого вона виконується.
Задача 1.25. Плоский конденсатор ємністю С = 1 нФ, обкладки котрого щільно прилягають до пластини діелектрика з проникністю ε = 5, підключено до джерела напруги U = 100 В. Визначити, яку роботу А треба виконати, аби витягти пластину з конденсатора, не відмикаючи його від джерела. Тертя відсутнє.
Задача 1.21
Три однакові точкові заряди q = 1 нКл розташовано у вершинах правильного трикутника зі стороною a = 20 см, рис. 21а.
Визначити
роботу A, яку треба виконати, аби один із зарядів перенести на середину протилежної сторони трикутника, рис. 21б.
|
Дано: q = 1 нКл
a = 20 см
b = (а/2)
|
|
A - ?
|
Розв'язання
Шукана робота A дорівнює зміні (різниці кінцевого Wк і початкового Wп значень) енергії взаємодії зарядів через зміну їхнього взаємного розташування (п. 1.3):
|
A = Wк – Wп. |
|
Величини W дорівнюють сумі енергій попарної взаємодії зарядів
|
W = W12 + W13 + W23, |
(1) |
які визначаються формулою (1.30). Тож, ураховуючи, що величини зарядів і відстані a між ними в початковому положенні є однакові, маємо:
|
\(W_{п}=3\frac{kq^{2}}{a}\). |
(2) |
У кінцевому положенні відстань між крайніми зарядами дорівнює а, а між суміжними — b = (a/2). Тож, у виразі (1)
|
\(W_{13}=\frac{kq^{2}}{a}\) і \({{W}_{12}}={{W}_{23}}=2\frac{k{{q}^{2}}}{a}\). |
(3) |
Відповідно, кінцева енергія системи
|
\(W_{к}=5\frac{kq^{2}}{a}\), |
|
і шукана робота
|
\({{А}=2\frac{kq^{2}}{a}}\) = 90 нДж. |
|
Задача 1.22
Металеву кулю радіуса R = 10 см, яка містить заряд q = 100 нКл, з'єднали провідником із землею.
Визначити
кількість теплоти Q, що виділилась у провіднику.
|
Дано: R = 10 см = 0,1 м
q = 100 нКл= 10-7 Кл
|
|
Q - ? |
Розв'язання
У зарядженому провіднику надлишковий заряд є зосереджений на поверхні й розподілений по ній так, що всі його точки мають однакові потенціали φi = φ (див. п. 1.5)). Тож, розглядаючи заряджений провідник як систему точкових зарядів, для його електростатичної енергії за виразом (1.31) маємо:
\(W=\frac{1}{2}\varphi\sum\Delta{q}_{i}=\frac{1}{2}q\varphi\).
Потенціал провідної кулі із заданими радіусом і зарядом визначається формулою (1.18), отже її електростатична енергія дорівнює
\(W=\frac{q^{2}}{8\pi\varepsilon_{0}R^{2}}\).
У процесі розряджання кулі по заземлювальному провіднику протікає електричний струм, який супроводжується його нагріванням, тобто виділенням у провіднику тепла за рахунок електростатичної енергії. Тож за законом збереження енергії шукана кількість теплоти, що виділяється при повному розряджанні кулі, дорівнює її початковій електростатичній енергії:
\(Q=\frac{q^{2}}{8\pi\varepsilon_{0}R}\) = 4,5·10–4 Дж = 0,45 мДж.
Примітка. Заради строгості слід сказати, що при розряджанні не вся електростатична енергія кулі йде на нагрівання – певна її частка втрачається через електромагнітне випромінювання заземлювального провідника, що виникає внаслідок зміни в ньому величини струму. Але такі втрати є неістотними.
Задача 1.23
Заряджений до напруги U = 100 В конденсатор C1 = 10 мкФ з’єднують із незарядженим конденсатором С2 = 5 мкФ.
Визначити,
яка енергія \(\Delta{W}\) виділяється при цьому.
|
Дано: C1 = 10 мкФ = 10·10-6 Ф
С2 = 5 мкФ = 5·10-6 Ф
U = 100 В
|
|
W′ - ? |
Розв'язання
Система конденсаторів є електрично ізольованою, тож при підключенні другого конденсатора ємність системи зростає, а заряд лишається незмінним. Тому, згідно з формулою (1.32а), електростатична енергія системи зменшується, отже якась її частка перетворюється на інші форми, в даному випадку – в тепло, що виділяється в з’єднувальних провідниках, – та в енергію випромінювання іскри, котра може утворитися при з’єднуванні конденсаторів.
Таким чином, шукана енергія W′ = W1 –W2 дорівнює спадові енергії системи й за формулою (1.32а) складає:
W′ = $\frac{{{q}^{2}}}{2}\left( \frac{1}{{{C}_{1}}}-\frac{1}{{{C}_{1}}+{{C}_{2}}} \right)=\frac{{{q}^{2}}{{C}_{2}}}{2{{C}_{1}}\left( {{C}_{1}}+{{C}_{2}} \right)}$.
Відтак, виразивши за формулою (1.23) заряд як q = С1U, отримаємо остаточну відповідь:
W′ = $\frac{{{C}_{1}}{{C}_{2}}}{2\left( {{C}_{1}}+{{C}_{2}} \right)}{{U}^{2}}$ = 16,7 мДж.
У зарядженому від джерела напруги повітряному конденсаторі з енергією W0 повільно збільшують відстань між пластинами в n разів а) при відімкненому та б) при приєднаному джерелі.
Визначити,
Визначити роботу А, що виконується в кожному випадку, та пояснити, за рахунок чого вона виконується.
|
Дано: W0, n |
|
A -? |
Розв'язання
З механіки відомо (див. [І], п. 4.3), що робота, яка виконується над тілом, чи ним самим, дорівнює різниці кінцевого \(W\) та початкового \(W_{0}\) значень його повної механічної енергії:
|
\(A=W-W_{0}\). |
(1) |
Уданій задачі з умови зрозуміло, що кінетична енергія є неістотна, тож у виразі (1) фігурує лише кінцева \(W\) та початкова \(W_{0}\) електростатична енергія конденсатора, котра визначається формулами (1.32). При цьому безпосередньою причиною зміни енергії в кожному випадку є зменшення ємності конденсатора при збільшенні відстані між пластинами (див. формулу (1.26)) від якогось значення \({C_0}\) до
\(C=\frac{C_0}{n}\).
Випадок а). При при розсуванні пластин у відключеному конденсаторі його заряд не не змінюється. Тож за формулою (1.32а) кінцева енергія складає
\(W=\frac{q^{2}n}{2C_0}=nW_{0}\),
і шукана робота дорівнює
\(A=(n-1)W_0\).
При розсуванні пластин у відключеному конденсаторі для подолання кулонівського притягання до них треба прикладати зовнішню силу, яка й виконує знайдену роботу й збільшує енергію конденсатора.
Випадок б). При збільшенні відстані між пластинами в підключеному конденсаторі, попри зменшення ємності, напруга лишається рівною
\(U=\E\),
де \(\E\) – ЕРС джерела (див. Розділ ІІ, п. 1.2). При цьому за формулою (1.32б) енергія конденсатора змінюється від значення \(W_{0}=C_{0}\E^2/2\) до \(W=C_{0}\E^{2}/2n\), отже, згідно з виразом (1), виконується робота
\(A=-\frac{n-1}{n}W_{0}\).
Знак "–" у відповіді означає, що у випадку б) шукана робота виконується за рахунок енергії конденсатора і йде на подолання електричного опору з'єднувальних провідників та самого джерела при переміщенні "зайвих" зарядів із однієї пластини конденсатора на іншу.
Задача 1.25.
Плоский конденсатор ємністю С = 1 нФ, обкладки котрого щільно прилягають до пластини діелектрика з проникністю ε = 5, підключено до джерела напруги U = 100 В.
Визначити,
яку роботу А треба виконати, аби витягти пластину з конденсатора, не відмикаючи його від джерела. Тертя відсутнє.
|
Дано: C0 = 1 нФ = 10–9 Ф
ε = 5
U = 100 В |
|
A - ? |
Розв'язання
При вийманні діелектрика змінюються ємність С і енергія W конденсатора. Тож частина його заряду Δq = q1 – q2 перетікає через джерело з однієї обкладки на іншу, виконуючи відповідну роботу Аст = Δq·U проти так званих ''сторонніх'' сил (див. Розділ ІІ, п. 1.1), що підтримують на полюсах постійну напругу U. Таке перезаряджання конденсатора відбувається за рахунок роботи А зовнішньої сили, котру слід прикладати до пластини для виймання з конденсатора. Отже,
А = W2 – W1 + Аст
Далі, виразивши енергії конденсатора та роботу проти сторонніх сил через заряд за формулами (1.32в) і (1.13), отримаємо:
\(A=\frac{\left( {{q}_{1}}-{{q}_{2}} \right)U}{2}\).
Нарешті врахуємо, що q1 = CU і q2 = (C/ε)U, і отримаємо наступну відповідь:
\(A=\frac{\varepsilon -1}{\varepsilon }\cdot C{{U}^{2}}\) = 8 мкДж.
Рівновага й рух зарядів в електричному полі
|
Задачі на рівновагу і рух заряджених тіл в електричному полі принципово не відрізняються від подібних задач механіки. Тому при самостійному розв'язуванні рекомендованих задач за необхідності варто керуватися рекомендаціями посібника Механіка. Також нагадаємо, що при розгляді руху мікрочастинок (електронів, іонів, тощо) в зовнішніх електричних полях сили тяжіння є несуттєвими. |
Задача 1.26. За уявленнями класичної механіки електрони в атомах рухаються навколо ядер по колових орбітах, як планети навколо Сонця. Виходячи з цього, визначити швидкість v руху електрона в атомі Гідрогену, якщо радіус його орбіти r = 53 пм.
Задача 1.27. Дві однойменно заряджені кульки з масами M і m та зарядами Q і q , що закріплені на лінії однорідного горизонтального електричного поля з напруженістю E, вивільняють. Визначити відстань між кульками на момент, коли їхні прискорення зрівняються.
Задача 1.28. У плоску смугу завтовшки d = 10 см із перпендикулярним до її межі електричним полем напруженістю E = 100 В/см під кутом \(\alpha=30^{\circ}\) до напрямку поля влітає електрон, який пройшов прискорювальну напругу U0 = 2 кВ (див. рис. 28 у розв'язанні). Визначити: 1. З якою швидкістю v та під яким кутом \(\beta\) електрон вилетить з поля; 2. Найменшу напруженість поля E0, при якій електрон не зможе подолати смугу.
Задача 1.29. Протон починає рухатись із енергією K = 200 еВ у напрямку віддаленого вільного протона, що перебуває в стані спокою. Визначити, на яку найменшу відстань r перший протон наблизиться до другого.
Задача 1.30. Дві кульки з масами m1 = 50 г і m2 = 25 г та зарядами q1 = –120 мкКл і q2 = 30 мкКл на кінцях невагомого стрижня довжиною l = 1 м із закріпленою віссю обертання, що проходить через середину, перебувають у спокої. Нехтуючи розміром кульок та тертям в осі, визначити, якої максимальної швидкості vm вони набудуть після незначного поштовху, якщо йому передувало ввімкнення спрямованого донизу електричного поля напруженістю Е = 20 В/см.
Задача 1.26
За уявленнями класичної механіки електрони в атомах рухаються навколо ядер по колових орбітах, як планети навколо Сонця. Виходячи з цього,
визначити
швидкість v руху електрона в атомі Гідрогену, якщо радіус його орбіти r = 53 пм.
|
Дано: r = 53 пм = 5,3·10-11 м |
|
v - ? |
Розв'язання
Кулонівська сила (1.3а), надає електронові доцентрового прискорення ([I], ф-ли (1.28), (2.17)). Отже, за другим законом Ньютона
|
\(\frac{e^{2}}{4\pi\varepsilon_{0}r^{2}}=\frac{mv^{2}}{r}\) $\Rightarrow $ $v=\frac{e}{\sqrt{4\pi {{\varepsilon }_{0}}rm}}$. |
|
Урахувавши довідкові дані e = 1,6·10–19 Кл, m = 9,1·10-31 кг і ε0 = 8,85·10–12 Ф/м, отримаємо числову відповідь:
v = 2,2·106 м/с.
Задача 1.27
Дві однойменно заряджені кульки з масами M і m та зарядами Q і q , що закріплені на лінії однорідного горизонтального електричного поля з напруженістю E, вивільняють.
Визначити
відстань між кульками на момент, коли їхні прискорення зрівняються.
|
Дано: M, m
Q, q
E
|
|
r - ?
|
Розв'язання
Рух кожної кульки після вивільнення визначається дією сили тяжіння \(\vec{F}_{т}\), та електричної сили \(\vec{F}_{e}\), що складається із кулонівської сили \(\vec{F}_{k}\), що діє з боку іншої кульки, та сили \(\vec{F}_{п}\), зумовленої дією зовнішнього поля:
\(\vec{F}_{e}\) = \(\vec{F}_{k}\) + \(\vec{F}_{п}\).
Тож прискорення кульок складаються з двох компонент:
\(\vec{a}\) = \(\vec{g}\) + \(\vec{a}_{e}\)
і зрівнюються за умови \(\vec{a}_{e1}\) = \(\vec{a}_{e2}\), тобто, коли
|
\(\vec{a}_{k1}\) + \(\vec{a}_{п1}\) = \(\vec{a}_{k2}\) + \(\vec{a}_{п2}\). |
(1) |
Сила тяжіння обом кулькам надає однакового прискорення \(\vec{g}\), тому в процесі руху вони лишаються на лінії зовнішнього поля \(\vec{E}\) (рис. 27).
Тому, з урахуванням напрямків векторів, умову (1) можна переписати через модулі, як
|
|ап1 – аk1| = ап2 + аk2 $\Rightarrow$ |ап1 – ап2| = аk1 + аk2. |
|
Отже, з урахуванням другого закону Ньютона та те, що сили кулонівської взаємодії кульок мають однаковий модуль Fk, останню рівність можна записати, як
|
$\left| \frac{{{F}_{n1}}}{M}-\frac{{{F}_{n2}}}{m} \right|={{F}_{k}}\left( \frac{1}{M}+\frac{1}{m} \right)$. |
(1) |
Відтак, виразивши сили Fп і Fk за формулами (1.2) і (1.3а), після простих перетворень отримаємо співвідношення
$\left| Qm-qM \right|E=\frac{Qq\left( M+m \right)}{4\pi {{\varepsilon }_{0}}{{r}^{2}}}$
та наступну відповідь:
$r=\sqrt{\frac{Qq\left( M+m \right)}{4\pi {{\varepsilon }_{0}}\left| Qm-qM \right|E}}$.
Задача 1.28
У плоску смугу завтовшки d = 10 см із перпендикулярним до її межі електричним полем напруженістю E = 100 В/см під кутом \(\alpha=30^{\circ}\) до напрямку поля влітає електрон, який пройшов прискорювальну напругу U0 = 2 кВ.
Визначити:
1. З якою швидкістю v та під яким кутом \(\beta\) електрон вилетить з поля;
2. Найменшу напруженість E0, при якій електрон не зможе подолати смугу.
|
Дано: d = 10 см E = 100 В/см \(\alpha=30^{\circ}\) U0 = 2 кВ |
| v - ? E0 - ? |
Розв'язання
1. Кінетична енергія електрона на вході W0 дорівнює роботі прискорювального поля, а на виході її значення W є меншим на величину роботи електрона проти гальмівного поля. Отже, відповідно до формули (1.13),
| $W=e\left( {{U}_{0}}-U \right)$, |
(1) |
де U – напруга (різниця потенціалів) між кінцевим та початковим положеннями електрона. За умовою гальмівне поле є однорідним і перпендикулярним до поверхонь смуги. Тому величина U не залежить від відстані між початковою та кінцевою точками переміщення електрона в смузі й за співвідношенням (1.20) складає $U=Ed$. Отже, враховуючи формулу кінетичної енергії, з виразу (1), маємо:
| ${{v}^{2}}=\frac{2e}{m}\left( {{U}_{0}}-Ed \right)$ $\Rightarrow $ $v=\sqrt{\frac{2e\left( {{U}_{0}}-Ed \right)}{m}}$. |
(2) |
Обчислення дають
v = 1,88·107 м.


Кут вильоту електрона β (див. рис. 28-1) знайдемо, взявши до уваги, що електричне поле не впливає на перпендикулярну складову вектора швидкостізарядженої частинки:
|
$v\sin \beta ={{v}_{0}}\sin \alpha $ $\Rightarrow $ $\sin \beta =\frac{{{v}_{0}}}{v}\sin \alpha $, |
(3) |
де початкова швидкість
| ${{v}_{0}}=\sqrt{\frac{2{{W}_{0}}}{m}}=\sqrt{\frac{2e{{U}_{0}}}{m}}$. |
(4) |
Звідси для кута вильоту β маємо:
|
$\sin \beta =\sqrt{\frac{U}{U-Ed}}\sin \alpha $ = $\frac{1}{\sqrt{2}}$ $\Rightarrow $ β = 45°. |
2. Аби електрон не зміг подолати смугу гальмівного поля, його максимальне зміщення x уздовж напрямку поля має задовольняти умову:
|
x ≤ d. |
(5) |
Величина x залежить від модуля v0 (вираз (4)) і напрямку (кута α) початкової швидкості та величини прискорення електрона
$a=\frac{F}{m}=\frac{eE}{m}$,
і за законами кінематики (див. [І], ф-ла (1.18)) визначається рівнянням:
$v_{0}^{2}{{\cos }^{2}}\alpha =2ax$ $\Rightarrow $ $x=\frac{U}{E}{{\cos }^{2}}\alpha $.
Таким чином, у згоді з умовою (5),
|
$\frac{U}{E}{{\cos }^{2}}\alpha $ ≤ d $\Rightarrow $ E ≥ $\frac{U}{d}{{\cos }^{2}}\alpha $. |
|
Обчислення дають E ≥ 1,5 кВ, тож мінімальна напруженість у смузі гальмівного поля, при якій електрон не зможе її подолати, складає
Е0 = 150 В/см.
Задача 1.29
Протон починає рухатись із енергією K0 = 200 еВ у напрямку віддаленого вільного протона, що перебуває в стані спокою.
Визначити,
на яку найменшу відстань r0 перший протон наблизиться до другого.
|
Дано: K0 = 200 еВ = 3,2·10–17 Дж
|
|
r0 - ?
|
Розв'язання
Через кулонівське відштовхування перший протон буде рухатися сповільнено, а другий – прискорено без початкової швидкості. Отже, вони спочатку будуть наближатись, а згодом – віддалятись один від одного і на момент максимального зближення матимуть однакові імпульси ${{p}_{1}}$ та кінетичні енергії ${{K}_{1}}=\left( p_{1}^{2}/2m \right)$.
Позаяк зовнішні сили на протони не діють, їхній сумарний імпульс не змінюється й дорівнює початковому імпульсові першого ${{p}_{0}}$. Тому на момент максимального зближення імпульс кожного протона складає
${{p}_{1}}=\frac{{{p}_{0}}}{2}$,
а кінетична енергія
К1 = $\frac{1}{4}{{W}_{0}}$.
Отже, за законом збереження енергії
|
${W}_{0}=2\frac{1}{4}{{W}_{0}}+{{W}_{вз}}$ \(\Rightarrow\) ${{W}_{вз}}=\frac{{{W}_{0}}}{2}$, |
|
де ${{W}_{вз}}$ – енергія кулонівської взаємодії протонів, яка виражається формулою (1.28). Тож
$\frac{k{{e}^{2}}}{{{r}_{\operatorname{m}}}}=\frac{{{W}_{0}}}{2}$.
Звідси для шуканої найменшої відстані між протонами маємо:
\(r_{min}=\frac{2ke^{2}}{W_{0}}\).
Підставивши значення констант k = 9·109 м/Ф і e = 1,6·10–19 Кл, отримаємо наступну числову відповідь:
rmin = 14, 4·10–12 м = 14, 4 пм.
Задача 1.30. Дві кульки з масами m1 = 50 г і m2 = 25 г та зарядами q1 = –120 мкКл і q2 = 30 мкКл на кінцях невагомого стрижня довжиною l = 1 м із закріпленою віссю обертання, що проходить через середину, перебувають у спокої. Нехтуючи розміром кульок та тертям в осі,
визначити,
якої максимальної швидкості vm вони набудуть після незначного поштовху, якщо йому передувало ввімкнення спрямованого донизу електричного поля напруженістю Е = 20 В/см.
|
Дано: m1 = 50 г m2 = 25 г q1 = –120 мкКл q2 = 30 мкКл l = 1 м Е = 20 В/см |
|
vm - ? |
З механіки відомо ([І], розд. V]), що тіло із закріпленою віссю обертання є зрівноваженим, коли сумарний момент діючих сил відносно неї дорівнює нулю. При цьому рівновага є стійкою, якщо при виведенні тіла з положення рівноваги з'являється момент сил, який протидіє цьому. Тож спочатку важча кулька є розташована знизу на одній вертикалі з легшою, рис. 30а. Але після ввімкнення поля до сил тяжіння додаються ще й спрямовані вниз електричні сили (рис. 30б), причому, як легко підрахувати, для важчої кульки результуюча сила\(\vec{F}_{1}\) виявляється меншою, ніж для легшої \(\vec{F}_{2}\). Тому після зміщення при поштовху від вертикалі кульки почнуть прискорено обертатися навколо осі О й досягнуть максимальної швидкості, коли стрижень повернеться на 180° .

Швидкість кульок визначається їхньою кінетичною енергією, що за механікою ([І], розд. IV]) дорівнює сумарній роботі сил тяжіння AT і електричних сил AE:
$\frac{\left( {{m}_{1}}+{{m}_{2}} \right){{v}^{2}}}{2}={{A}_{T}}+{{A}_{E}}$ $\Rightarrow $
|
$v=\sqrt{\frac{2\left( {{A}_{T}}+{{A}_{E}} \right)}{{{m}_{1}}+{{m}_{2}}}}$ |
(1) |
Таким чином, для визначення максимальної швидкості кульок треба знайти сумарну роботу вказаних сил на момент повороту стрижня на 180°, коли величина переміщення кожної кулька складе ${l}$. Тож, урахувавши напрямки переміщень та сил отримаємо:
для роботи сил тяжіння ([I], ф-ла (4.1а),
${{A}_{T}}=\left( {{m}_{2}}-{{m}_{1}} \right)gl$,
і для електричних сил (ф-ла (1.13))
${{A}_{E}}$= $\left( {{q}_{2}}+\left| {{q}_{1}} \right| \right)El$.
Відтак, підставивши ці величини у вираз (1), отримаємо наступну загальну відповідь:
${{v}_{m}}=\sqrt{\frac{2l}{{{m}_{1}}+{{m}_{2}}}\left( \left( {{m}_{2}}-{{m}_{1}} \right)g+\left( {{q}_{2}}+\left| {{q}_{1}} \right| \right)E \right)}$.
Обчислення дають
vm = 1,15 м/с.
Наостанок варто зауважити таке. Після повороту стрижня на 180° (рис. 30в ) знаки моментів сил змінюються на протилежні, й рух кульок стає сповільненим. Тож за відсутності тертя вони мали би повернутися у початкове положення з вихідною швидкістю й продовжити рух, як було розглянуто. І так знов і знов. Але насправді через невідворотні втрати механічної енергії кульки трохи не дістануться початкового положення й почнуть рухатися у зворотньому напрямі. Тому стрижень буде не обертатися, а здійснювати коливання, котрі через тертя поступово загасатимуть і згодом припиняться. При цьому кульки опиняться в незвичному рівноважному положенні, в якому важка розташована над легкою.
3. Задачі для самостійної роботи
При розв'язуванні задач електростатики рекомендується використовувати загальні поради по організації й оформленню розв'язку (див. "Етапи розв'язування задач").
Наведені приклади розв'язування задач поділені за рівнем складності на групи А, Б і В.
Закон Кулона
|
Рівень А |
|
|
1.31. |
Електричні заряди двох хмар, які віддалені одна від одної на 30 км, дорівнюють 20 Кл і – 30Кл. Визначити силу притягання між хмарами. [6 кН ] |
|
1.32. |
Дві кульки із загальним зарядом 50 мкКл, що віддалені одна від одної на 2 м, відштовхуються із силою 0,9 Н. Знайти заряд кожної кульками. [40 мкКл, 10 мкКл] |
|
1.33. |
Дві кульки із зарядами q1 і 2q1 закріплено на відстані 50 см одна від одної. Де слід розмістити третю заряджену кульку, аби вона перебувала в рівновазі, якщо заряди перших двох: 1) однойменні і 2) різнойменні? Якою буде рівновага в кожному випадку? [1) всередині на відстані 20,7 см від q1; 2) на відстані 120,7 см від q1. Нестійкою] |
|
1.34. |
Коли підвішену на нитці заряджену кульку маси 5 г розмістили над закріпленою кулькою із зарядом тієї ж величини, натяг нитки подвоївся. Визначити величину зарядів кульок. [≈ 1,2 мкКл] |
|
1.35. |
Два заряджені кульки, розміщені у воді (ε1 = 81) на відстані 3 см одна від одної, взаємодіють із певною силою F. На якій відстані слід розмістити кульки в гасі (ε2 = 2), аби сила взаємодії між ними не змінилася? [≈ 19 см] |
|
Рівень Б |
|
| 1.36. |
Дві однаково заряджені мідні (ρ = 8,9 г/см3) кулі, масою 300 г і радіусом 2 см кожна, на гладкій горизонтальній поверхні перебувають у рівновазі. Визначити густину заряду на кулях. [≈ 5 нКл/м2] |
| 1.37. |
Дві маленькі кульки із зарядами 24 нКл і 6 нКл закріплено на певній відстані одна від одної. Як і в скільки разів зміниться сила взаємодії між кульками, якщо їх на мить з'єднати тонкою дротиною? [збільшиться в 1,6 раза] |
|
1.38. |
Дві однакові металеві кульки масою по 250 мг, що підвішені в дотик на невагомих нитках довжиною 1 м, після заряджання розійшлися на відстань 6 см. Який заряд отримали кульки? [10,8 нКл ] |
|
1.39. |
Дві кульки з масою 20 г і зарядом 50 нКл кожна, що підвішені в дотик на нитках довжини 2 м, розійшлися на малий кут φ. Знайти його величину. $\left[ \varphi =\sqrt[3]{\frac{2k{{q}^{2}}}{mg{{l}^{2}}}}=2,2{}^\circ \right]$ |
|
1.40. |
Дві однойменно заряджені легенькі кульки (ρ = 1,5 г/см3) кульки, що підвішені на гачку на однакових нитках, опускають у непровідну рідину (ρ0 = 0,8 г/см3). Визначити її діелектричну проникність, якщо кут розходження ниток не змінився. [2,15] |
|
1.41. |
Три однакові заряди по q = 10 нКл розташовані у вершинах правильного трикутника, а четвертий q0 – у центрі. Визначити величину q0, якщо система перебуває в рівновазі. Чи є стійкою ця рівновага? [–5,77 нКл; ні] |
| Рівень В | |
| 1.42. |
Відстані та сили взаємодії між точковими зарядами q1, q2, q3 відомі й складають: між першим і другим – r1, F1, другим і третім – r2, F2, третім і першим – r3, F3. Встановити величини зарядів. \(\left[ {{q}_{1}}=\frac{{{r}_{1}}{{r}_{3}}}{{{r}_{2}}}\sqrt{\frac{{{F}_{1}}{{F}_{3}}}{k{{F}_{2}}}} \right]\), $k=\left( 1/4\pi {{\varepsilon }_{0}} \right)$. (Кожний з наступних двох виразів виходить із попереднього шляхом циклічної перестановки індексів у правій частині проти годинникової стрілки). |
| 1.43. |
Заряджена кулька обертається із кутовою швидкістю 5 рад/с по колу радіуса 3 см навколо закріпленої кульки із зарядом –5 нКл. Визначити питомий заряд рухомої кульки, тобто відношення її електричного заряду до маси. [15 мкКл/кг] |
| 1.44. |
Три маленькі кульки масою по 20 мг підвішено в одній точці на невагомих нитках довжиною 30 см. Які однакові заряди треба надати кулькам, аби кожна з ниток утворила кут 30° з вертикаллю? [22,4 нКл] |
| 1.45. | Підвішена на тоненькій нитці незаряджена кулька маси 2,5 г обертається по колу радіуса 30 см із кутовою швидкістю 1 рад/с навколо закріпленої незарядженої кульки. Якої величини однакові заряди треба надати кулькам, аби перша рухалася тією самою траєкторією з подвоєною частотою? [150 нКл; –150 нКл] |
Напруженість і потенціал
|
Рівень А |
||
|
1.46. |
Чи можуть перетинатися а) силові лінії та б) еквіпотенціальні поверхні електричного поля? Чому? [а), б) –ні] |
|
|
1.47. |
Визначити напруженість і потенціал електричного поля посередині між точковими зарядами 6 нКл і –6 нКл, які закріплено на відстані 40 см один від одного. [1,35 кВ/м; 0] |
|
| 1.48. |
Три точкові заряди по –1,3 нКл кожен знаходяться у вершинах правильного трикутника зі стороною 10 см. Визначити напруженість і потенціал електричного поля в центрі трикутника. [0; –608 В] |
|
| 1.49. |
Точкові заряди q, 2q, 3q i 4q розташовані у вершинах квадрата. Визначити можливі значення напруженості електричного поля системи в центрі квадрата, якщо перший заряд створює в ньому поле 10,6 В/м. [15,0 В/м; 23,7 В/м; 30,0 В/м] |
|
| 1.50. |
Металева куля діаметром 8 см має заряд 2 нКл. Визначити напруженість і потенціал електричного поля кулі на відстанях 2 см, 4 см і 6 см від центра. [0, 450В; 11,25 кВ/м, 450В; 5 кВ/м, 300 В] |
|
| 1.51. |
На відстані 10 см від поверхні зарядженої провідної сфери радіусом 5 см , потенціал електричного поля складає 20 В. Чому він дорівнює в центрі сфери? [60 В] |
|
| 1.52. |
Заряджена кулька масою 2 г висить на нитці між двома горизонтальними пластинами із відстанню між ними 10 см і напругою 500 В. Чому дорівнює заряд кульки, якщо при вимиканні напруги сила натягу нитки зменшилася вдвічі [4 мкКл] |
|
| 1.53. |
Дві паралельні плоскі металеві пластини заряджено з густиною \(\left| {{\sigma }_{1}} \right|\) = 35 нКл/м2 та $\left| {{\sigma }_{1}} \right|$ = 17,5 нКл/м2. Визначити напруженість електричного поля між Е′ та поза Е′′ пластинами. [Е′ = 10 В/см, Е′′ = 30 В/см при σ1·σ2 > 0; Е′ = 30 В/см, Е′′ = 10 В/см при σ1·σ2 < 0] |
|
| 1.54. |
Визначити в скільки разів зміниться напруга між двома паралельними зарядженими плоскими пластинами при зміні відстані між ними на 20%. [1,2 або 1,25] |
|
Рівень Б |
||
| 1.55. |
Три точкові заряди по 1 нКл розташовані у вершинах прямокутного трикутника з гострим кутом 30 і гіпотенузою 10 см. Визначити напруженість електричного поля в точці перетину гіпотенузи з перпендикуляром, що опущений на неї з вершини прямого кута. [136,5 В/м] |
|
| 1.56. |
Кожен із зарядів, що знаходяться на кінцях гіпотенузи "єгипетського" трикутника, створює в місці розташування іншого електричне поле з напруженістю 100 В/м. Визначити модуль і напрям (кут із гіпотенузою) вектора напруженості поля в третій вершині вказаного трикутника при а) однакових і б) різних знаках зарядів. [318,7 В/м; а) 96,9°; б) 23,8°] |
|
| 1.57. |
Електричне поле створюється однаковими точковими зарядами, що розташовані в трьох вершинах квадрата. Визначити відношення а) напруженостей і б) потенціалів поля в центрі та четвертій вершині. [η1 ≈ 1; η2 ≈ 1,6] |
|
|
1.58. |
Кожен із двох рівних рівних за величиною зарядів, які розташовано у вершинах правильного трикутника зі стороною 10 см, створює в третій вершині поле з потенціалом 50 В . Визначити напруженість поля в третій вершині, коли заряди: а) однойменні; б) різнойменні. [а) 866 В/м; б) 500 В/м]. |
|
| 1.59. |
Однакові за величиною заряди, розташовані в двох вершинах правильного трикутника, створюють у третій поле з такою самою напруженістю Е, як і кожен окремо. Чому дорівнює його потенціал? [0] |
|
| 1.60. |
Два рівних за величиною заряди, що розташовані у вершинах правильного трикутника зі стороною 10 см, створюють у третій вершині поле з потенціалом 116 В. Чому дорівнює напруженість поля в цій точці? [100 В/м] |
|
|
1.61. |
На кінцях стрижня довжиною 1 м закріплено різнойменні точкові заряди, котрі вчетверо різняться за величиною. Визначити відстань від меншого заряду до точки на лінії стрижня, де дорівнює нулю: а) напруженість; б) потенціал електричного поля зарядів. [а) 1 м назовні; б) 20 см всередині] |
|
|
1.62. |
Два різнойменні точкові заряди, що вдвічі відрізняються за величиною, закріплено на відстані 1,5 м один від одного. Визначити напруженість електричного поля між зарядами в точці з нульовим потенціалом, якщо в ній потенціал поля кожного заряду дорівнює 90 В. [270 В/м] |
|
| 1.63. |
Сферична краплина, що заряджена до потенціалу 90 В, при падінні на незмочувану нею поверхню розбилася на 27 однакових крапельок. Визначити їхні потенціали. [10 В] |
|
| 1.64. |
У центр провідної сферичної оболонки із внутрішнім радіусом 2 см і товщиною 1 см вміщено точковий заряд 9 мкКл. А). Визначити густину індукованих зарядів на поверхнях оболонки; Б). Чи зміниться їхній розподіл по поверхнях при зміщенні точкового заряду з центра? Як і чому? [0,18 мкКл/см2; на внутрішній так, на зовнішній ні] |
|
| 1.65. |
На дві плоскі металеві пластини з площею 100 см2 і відстанню між ними 1 мм подано напругу 5оо В. Визначити силу взаємодії між пластинами, якщо густина заряду на пластинах дорівнює 6 мкКл/м2. [15 мН] |
|
| 1.66 |
Визначити поверхневі густини заряду на двох різнойменно заряджених паралельних площинах, якщо між ними напруженість електричного поля дорівнює 2 В/см, а поза ними — 8 В/см. [≈ 3,5 нКл/м2; ≈ 7 нКл/м2] |
|
| 1.67 |
У простір між двома зарядженими з поверхневою густиною 100 нКл/м2 і 50 нКл/м2 площинами паралельно внесли металеву пластину площею 400 см2. Визначити заряди, що з'явилися на її поверхнях. [±2 нКл/м2 ] |
|
| 1.68. |
Підвішену на нитці кульку масою 1 г і зарядом 1 мкКл, внесено в простір між двома вертикальними металевими пластинами, що перебувають під напругою 1 кВ. Визначити відстань між пластинами, якщо нитка відхилилася на кут 30°. [≈ 5,8 см] |
|
|
Рівень В |
||
| 1.69. |
У трьох вершинах правильного тетраедра зі стороною 1 м розміщені заряди величиною 20 нКл кожен. Знайти напруженість та потенціал електричного поля в четвертій вершині. [≈ 350 В/м] |
|
| 1.70. |
Два паралельні кільця з радіусом R і зарядом q і –q розташовані на спільній осі на відстані l одне від одного. Визначити різницю потенціалів між центрами кілець. $\left[ \frac{q}{2\pi {{\varepsilon }_{0}}R}\left( 1-\frac{R}{\sqrt{{{R}^{2}}+{{l}^{2}}}} \right) \right]$ |
|
| 1.71. |
|
|
| 1.72. |
|
Провідники. Конденсатори
|
Рівень А |
||||
|
1.73. |
При з'єднанні двох віддалених однаково заряджених металевих куль тонким провідником одна з них втрачає половину заряду. Чому дорівнює відношення діаметрів куль? [3] |
|||
|
1.74 |
Визначити електричну ємність відокремленої провідної кулі з радіусом Землі R = 6400 км. [≈0,7 мФ] |
|||
| 1.75 |
Металеві кулю радіусом діаметром 5 см і оболонку діаметром 15 см з'єднано довгим тонким дротом. Визначити ємність з'єднання, якщо куля й оболонка: а) віддалені одна від одної; б) концентричні. [≈ 0,9 пФ; ≈ 0,7 пФ] |
|||
|
1.76 |
Ємність плоского повітряного конденсатора з квадратними пластинами дорівнює 0,1 пФ. Чому дорівнює ємність заповненого діелектриком із проникністю 2 такого конденсатора з удвічі меншими відстанню між обкладками та їхньому периметрі? [0,1 пФ] |
|||
| 1.77 |
Два однакових повітряних конденсатори з'єднані послідовно. Один з них заповнюють діелектриком із проникністю \(\varepsilon\). У скільки разів зміниться ємність системи? [Збільшиться в 2ε/(1+ε) разів] |
|||
| 1.78 |
Визначити ємність показаного на рис. 1.78, з'єднання конденсаторів, якщо С1 = 4 мкФ, С2 = 6 мкФ, С3 = 10 мкФ і С4 = 5 мкФ. [6 мкФ] |
|||
| 1.79 |
Визначити загальну ємність конденсаторів, з'єднаних так, як показаний на рис. 1.79, якщо С1 = 10 мкФ, С2 = 15 мкФ, С3 = 6 мкФ, С4 = 2 мкФ. [7,5 мкФ] |
|||
| 1.80 |
|
|||
| 1.81 |
|
|||
| 1.82 |
Два конденсатори, ємності котрих відрізняються вдвічі, з'єднали послідовно й підключили до джерела з напругою 120 В. Визначити напругу на кожному конденсаторі. [80 В і 40 В] |
|||
| 1.83 |
Плоский конденсатор з відстанню між пластинами 0,5 мм зарядили до напруги 10 В і від’єднали від джерела. Якою стала напруга на конденсаторі, якщо після цього відстань між його пластинами збільшили до 5 мм? [100 В] |
|||
| 1.84 |
Підключений до акумулятора конденсатор із діелектриком має заряд 1,2 нКл. Яким він стане після видалення з конденсатора діелектрика, якщо його проникність складає 6? [1 нКл] |
|||
|
Рівень Б |
||||
| 1.85 |
Провідну кулю із зарядом 5 нКл і потенціалом 40 В з’єднують тонким провідником із віддаленою другою провідною кулею із зарядом утричі і потенціалом – удвічі більшими, ніж у першої. Визначити, який заряд перейшов із однієї кулі на іншу та яким став потенціал першої кулі. [3 нКл; 64 В] |
|||
|
1.86 |
Поблизу зовнішньої поверхні згорнутого в циліндр великого зарядженого листа жерсті напруженість електричного поля складає 100 В/м. Якою вона стане, коли лист розпрялять? Чому? [5о В/м] |
|||
|
1.87 |
По двох близько розташованих паралельних плоских пластинах площею 1 м2 кожна рівномірно розподілено заряди 6 мкКл та –15мкКл, відповідно. Визначити різницю потенціалів між пластинами. [100,0 В] |
|||
|
1.88 |
У підключений до джерела напруги плоский конденсатор паралельно до обкладок вміщують діелектричну пластинку з товщиною, що втричі тонкіша за зазор між обкладками. Визначити проникність діелектрика, якщо при цьому заряд конденсатора зменшується на 20%. [2] |
|||
| 1.89 |
У зазор між обкладками зарядженого плоского конденсатора ввели пластину діелектрика з проникністю \(\varepsilon=5\) і товщиною в n = 3 рази меншою за відстань між обкладками (рис. 1.89). Визначити, у скільки разів змінилася напруга на конденсаторі.
|
|||
| 1.90 |
Плоский повітряний конденсатор з відстанню між обкладками 10 мм зарядили і відключили від джерела. Якої товщини скляну (ε = 2) пластинку розмістити між обкладками, аби напруга на конденсаторі зменшилась у 3 рази? [8 мм ] |
|||
| 1.91 |
Конденсатор ємністю 1 мкФ витримує максимальна напругу 6 кВ, а конденсатор ємністю 2 мкФ – 4 кВ. Яку максимальну напругу можна подати на ці два конденсатори при їхньому послідовному з'єднанні? [9 кВ] |
|||
| 1.92 |
На батарею конденсаторів, ємності котрих у мкФ позначені на рис. 1.92, у показаних точках подано напругу 8 В. Визначити заряди конденсаторів C1 – C6 у мкФ. [q1 = 8; q2,q6 = 12; q4 = 32; q3,q5 = 15] |
|||
| 1.93 |
Визначити ємність з'єднань конденсаторів Саб (рис.93), якщо всі конденсатори мають однакову ємність 10 мкФ. [а) 30 мкФ; б) 10 мкФ] |
|||
| 1.94 |
У схемі рис. 1.94 ємність батареї конденсаторів не змінюється при замиканні ключа . Яку ємність має при цьому конденсатор Сх? [С/2]
|
|||
|
Рівень В |
||||
| 1.95 |
|
|||
| 1.96 |
|
|||
| 1.97 |
|
|||
| 1.98 |
|
|
1.99 |
|
Робота та енергія електричного поля
| Рівень А | ||
| 1.100 |
Обчислити енергію взаємодії системи трьох однакових точкових зарядів 3,3 мккЛ, які розташовані у вершинах правильного трикутника із стороною 1 м. [0,3 Дж] |
|
| 1.101 |
Дві кульки із величиною (модулем) заряду 20 мКл і 10 мКл перемістили так, що їхні потенціали змінилися (по модулю) на 50 В і 200 В, відповідно. Яку роботу довелося виконати для цього? [± 1,5 мДж] |
|
| 1.102 |
Два позитивні й негативний віддалені один від одного заряди величиною по 2 мкКл переміщують у вершини правильного трикутника зі стороною 15 см. Визначити роботу, яку при цьому виконує електричне поле зарядів. [240 мДж] |
|
| 1.103 |
Невагомий штир довжиною 1,2 м із шарнірно закріпленим одним кінцем і зарядженою кулькою на другомукінці лежить на горизонтальній поверхні, вміщеній у паралельне до неї електричне поле з напруженістю 200 В/см. Нехтуючи тертям у шарнірі, знайти роботу, яку треба виконати, аби поставити штир вертикально при масі кульки 75 г і заряді 250 мкКл. [1,25 Дж] |
|
| 1.104 |
При збільшенні напруги на конденсаторі ємністю 1 мкФ у 3 рази його енергія зросла на 40 мДж. Визначити початкову напругу та енергію електричного поля конденсатора. [100 В, 5 мДж] |
|
| 1.105 |
|
|
| Рівень Б |
||
| 1.106 |
Три точкові заряди по 1мкКл кожен розташовані у вершинах правильного трикутника зі стороною 20 см. Яку роботу треба виконати, аби один із них розмістити заряд посередині між двома іншими, вони при цьому лишаються нерухомими? [≈ 90 мДж] |
|
| 1.107 |
Аби наблизити один заряд до закріпленого іншого на відстань у n разів меншу за початкову, довелося виконати роботу A1. Визначити роботу A2, котру було виконано на другій частині шляху від точки, розташованої посередині між крайніми. [ А2 = А1n/(n+1)] |
|
| 1.108 |
Показати, що при зміні відстані між пластинами зарядженого повітряного плоского конденсатора виконується робота, рівна зміні енергії його електричного поля. |
|
| 1.109 |
Зазор між пластинами плоского конденсатора зменшили в 2 рази. Визначити в скільки разів змінилася а) енергія та б) об'ємна густина енергії електричного поля конденсатора коли перед зближенням пластин конденсатор: 1) відключили від джерела; 2) не відключали. [1а) зменшилась у 2 рази; 1б) не змінилась; [2а) збільшилась у 2 рази; 2б) збільшилась у 4 рази] |
|
| 1.110 |
Енергія зарядженого плоского конденсатора, обкладки котрого прилягають до пластини діелектрика з проникністю 5, дорівнює 10 мкДж. Знайти роботу, яку треба виконати, аби подвоїти відстань між пластинами. [50 мкДж] |
|
| 1.111 |
Імпульсне точкове зварювання провідників здійснюють за допомогою розряду батареї конденсаторів з ємністю 1000 мкФ і напругою 1,5 кВ. Визначити ККД зварюваня при тривалості розрядного імпульсу 2 мкс і середній потужності 22,5 МВт [4%] |
|
| 1.112 |
Паралельно до обкладок зарядженого і відключеного від джерела плоского конденсатора вмістили пластинку діелектрика з проникністю 5 і товщиною в чверть зазору між обкладками. Визначити, як і наскільки (%) змінилась середня густина енергії поля в конденсаторі. [зменшилася на 20%] |
Рух зарядів в електричному полі
| 1.113. |
Кулька з питомим зарядом (q/m) = 1,25 мКл/кг, що починає падати, за чверть відстані до точки падіння стрічає на шляху однойменно заряджену металеву горизонтальну сітку й після її проходження подвоює свою швидкість. Визначити поверхневу густину заряду сітки, вважаючи її електричне поле однорідним. [177 нКл/м2] |
|
| 1.114. |
По горизонтальній дошці, що вміщена у вертикальне електричне поле з напруженістю 1 кВ/м на відстані 3 м від підлоги, котиться із швидкістю 3 м/с кулька з питомим зарядом 6 мКл/кг. На якій горизонтальній відстані від краю дошки кулька впаде на підлогу без урахування тертя та опору повітря? [1,5 м, або 3 м] |
|
| 1.115. |
У заряджений плоский конденсатор із довжиною пластин 3 см і відстанню між ними 1,6 см біля краю пластини під кутом 15° влітає електрон. За якої найменшої напрузі на конденсаторі він не зможе пролетіти наскрізь при початковій швидкості 1 Мм/с ? [1,5 В] |
|
| 1.116. |
Біля краю горизонтальної пластини, що вміщена у вертикальне електричне поле з напруженістю 100 В/м під кутом 45°, влітає й на відстані 30 см падає на пластину частинка масою 0,1 г і зарядом 500 нКл. Якою була би ця відстань за відсутності поля? [20 см; 60 см] |
|
| 1.117. |
Позитивно заряджений брусок, пройшовши без початкової швидкості певну відстань S по похилій площині з кутом нахилу 35°, виходить на горизонтальну поверхню й на такій самій відстані зупиняється. Визначити питомий заряд бруска (відношення заряду до маси), якщо на всьому шляху він рухається з коефіцієнтом тертя 0,4 вбік горизонтального електричного поля з напруженістю 100 В/м. [8,5 мКл/кг] |
|
| 1.118. |
Дві однакові порошинки масою по 1 мг і зарядом по 0,2 мкКл рухаються в зустрічному напрямі й, наблизившись до відстані 4 мм, розлітаються. Визначити швидкість, до якої вони розженуться по тому. [300 м/с] |
|
| 1.119. |
Кулька із зарядом 10 мкКл і масою 10 г, що випущена з великої відстані зі швидкістю 120 м/с, влучає по нормалі й навиліт пробиває закріплену заряджену сферичну оболонку радіусом 5 см і зарядом 20 мкКл. Нехтуючи втратами механічної енергії, визначити час перебування кульки всередині оболонки. [1,5 мс] |
|
1.120. |
У рівномірно заряджену сферичну оболонку радіусом 15 см і масою 50 г та зарядом 50 мкКл влучає кулька масою 10 г і зарядом 10 мкКл, яку випущено з великої відстані. Вважаючи удар центральним і нехтуючи втратами енергії, визначити: а) при якій найменшій початковій швидкості кулька прорве оболонку та б) час її руху всередині оболонки при початковій швидкості 100 м/с. [а) ≈ 85 м/с; б) 7,5 мс] |
Розділ ІІ. Постійний електричний струм
|
Електричний струм відіграє важливу роль у житті людини. Він дозволяє майже миттєво (зі швидкістю 3·108 м/с) переносити енергію від генераторів на електростанціях до найвіддаленіших споживачів. Енергія електричного струму є високоекологічна і легко перетворюється на інші види. Тому значна частина енергії, яку використовує людина, виробляється у формі енергії електричного струму. Далі подано: 2. Приклади розв’язування задач 3. Задачі для самостійної роботи
|
1. Теоретичні відомості
Електричним струмом називають перенесення електричного заряду, що створюється упорядкованим рухом заряджених частинок – носіїв струму. В наступних темах розглянуто основні властивості постійного струму, тобто струму незмінного напрямку:
1.1. Характеристики електричного струму
1.3. З'єднання резисторів і джерел
1.1. Характеристики та умови існування електричного струму
|
Електричний струм характеризується величиною і напрямом, за який прийнято напрям перенесення позитивного заряду. Тож напрям струму збігається з напрямом упорядкованого руху позитивних і є протилежним до напрямку руху негативних носіїв струму (рис. 2.1). Примітка. В твердих провідниках струм створюється електронами і є спрямований протилежно до напрямку реального руху носіїв. Але через електричну нейтральність речовини переміщення в ній негативного заряду є рівнозначним до такого самого зворотнього переміщення позитивного заряду. Тому далі задля зручності будемо вважати носії позитивно зарядженими.
|
|
Кількісною характеристикою струму є величина, що називається силою струму й визначає швидкість перенесення заряду по провіднику. А саме, сила постійного струму І дорівнює відношенню заряду, що проходить крізь переріз провідника, до часу його проходження:
Якщо струм змінюється з часом, то аналогічне відношення заряду до проміжку часу
визначає середню силу струму за цей проміжок. При неперервній зміні струм у кожний момент визначається миттєвою силою струму, яка є границею відношення (2.1а), тобто похідною:
Сила струму вимірюється в амперах (А). Одиниця 1А визначається через магнітну взаємодію електричних струмів і є основною в системі СІ. Це означає, що одиниці інших електричних і магнітних величин прямо чи опосередковано визначаються через ампер. До прикладу, відповідно до означення (2.1), одиниця заряду 1 Кл = 1 А·с, тобто один кулон дорівнює кількості електрики, що при силі струму один ампер проходить крізь переріз провідника за одну секунду. |
|
У теорії й на практиці важливою характеристикою електричного струму також є густина струму j – відношення сили струму до площі поперечного перерізу провідника:
Густина струму вимірюється в ”амперах на квадратний метр “ (A/м2) . У техніці зазвичай використовують кратну одиницю 1 А/мм2 = 106 А/м2.
Густина струму залежить від концентрації носіїв n, їхнього заряду e та швидкості впорядкованого руху u. Дійсно, в шарі провідника товщиною l і площею поперечного перерізу S (рис. 2.2) міститься заряд q = enSl, який проходить крізь переріз провідника за час t = (l/u). Отже, з означень (2.1) і (2.3) виходить, що густина та сила струму є прямо пропорційні швидкості впорядкованого руху носіїв струму:
|
|
Будь-яка речовина містить однакову кількість негативно та позитивно заряджених елементарних частинок, між якими діють кулонівські сили притягання, котрі перешкоджають (створюють “опір”) упорядкованому рухові носіїв. Тому для його подолання на носії мають діяти так звані “сторонні сили” – якісь сили не електростатичної природи. На практиці сторонні сили створюються за допомогою спеціальних пристроїв —“джерел струму” (батарейок і акумуляторів, фотоелементів, потужних індукційних генераторів, тощо). Наявність джерела є однією з двох обов'язкових умов існування електричного струму. Другою є замкненість провідника, позаяк різнойменні заряди, що одразу виникають на кінцях незамкненого провідника під дією сторонніх сил, своїм кулонівським полем нівелюють їхню дію й унеможливлюють подальший упорядкований рух носіїв. |
|
З'єднані між собою джерела та різні пристрої, що утворюють один, або декілька замкнених провідних контурів, називається електричним колом. Розглянемо, як працює найпростіше електричне коло, в якому джерело струму та з'єднані з ним пристрої утворюють лишень один провідний контур, як схематично показано на рис. 2.3.
Як щойно говорилося, у розімкненому колі надлишкові заряди на полюсах (клемах) джерела не створюють струму. Проте вони створюють всередині та назовні джерела кулонівське електричне поле ${{\vec{E}}_{к}}$, під дією котрого в момент замикання кола носії струму починають рухатися по зовнішній ділянці до протилежно зарядженого полюса і частково нейтралізують його та послаблюють кулонівське поле. Через це сторонні сили ${{\vec{F}}_{ст}}$ отримують перевагу над кулонівськими ${{\vec{F}}_{k}}$, тож “підхоплюють” прибулі носії і “перетягають” їх всередині джерела у вихідне положення. Цей процес іде неперервно й створює в колі циркуляцію заряду, тобто – електричний струм. Отже, джерело струму в колі діє подібно до насоса, який переганяє рідину від вхідного до вихідного отвору, примушуючи її циркулювати по замкненому трубопроводу.
|
1.2. Закон Ома
Спад напруги та електрорушійна сила (ЕРС). Сили, що діють на носії в провіднику зі струмом, виконують роботу А, котра на довільній ділянці кола складається з роботи сторонніх Aст і кулонівських Ak сил: A = Aст + Ak |
Ця робота є прямопропорційною до величини перенесеного заряду, тож і до часу протікання струму. Але
відношення роботи, що виконується над носіями на даній ділянці кола, до перенесеного заряду
|
$U=\frac{A}{q}=\frac{{{A}_{ст}}+{{A}_{k}}}{q}$ |
(2.5) |
визначається лише силами, що діють на носії, та здатністю ділянки проводити струм і називається спадом напруги.
Можна сказати, що спад напруги визначає сумарну енергетичну спроможність сторонніх та кулонівських сил, які діють на носії струму на заданій ділянці кола. При цьому
відношення роботи сторонніх сил до величини перенесеного заряду
|
$\E=\frac{{{A}_{cт}}}{q}$ |
(2.6) |
називається електрорушійною силою (ЕРС)
і є основною характеристикою джерела струму.
Для сил кулонівського поля аналогічне відношення за формулою (1.13) дорівнює різниці потенціалів на кінцях ділянки:
|
$\frac{{{A}_{k}}}{q}$ = ${{\varphi }_{1}}-{{\varphi }_{2}}$. |
(2.6а) |
Таким чином, вираз (2.5) для спаду напруги на довільній ділянці електричного кола набуває вигляду:
|
U = φ1 – φ2 + $\E$. |
(2.7) |
Електричний опір. Продовжуючи аналогію між електричним струмом й течією рідини (п. 1.1), вкажемо, що так само, як труба перешкоджає протіканню рідини, провідник чинить спротив перенесенню по ньому заряду. Цей спротив, як і в трубі з водою, зростає із збільшенням довжини l та зменшенням площі перерізу провідника S. Його кількісна міра називається електричним опором R і визначається, як
|
$R=\rho \frac{l}{S}$, |
(2.8) |
де величина ρ називається питомим опором і є табличною характеристикою речовини провідника.
Величини R(Ом) і ρ(Ом ·м) залежать від температури. Для металів і сплавів при не наднизьких температурах ця залежність є лінійною і має вигляд:
|
\(\rho=\rho_{0}(1+\alpha{t})\); |
(2.9) |
| \(R=R_{0}(1+\alpha{t})\). |
(2.9а) |
де t – температура в °С, \(\rho_{0}\) та \(R_{0}\) – питомий опір і опір провідника при t = 0°С, і α (1/К) – температурний коефіцієнт опору, котрий дорівнює відносній зміні питомого опору при зміні температури провідника на одиницю:
|
\(\alpha=\frac{\rho-\rho_{0}}{\rho_{0}t}\) |
|
і є табличною величиною.
Закон Ома. На вибраній ділянці довільного кола із струмом на носії можуть діяти або тільки сили кулонівського поля, або кулонівські та сторонні сили за наявності на ній джерела струму. В першому випадку ділянка зветься однорідною, а в другому – неоднорідною. При цьому в обох випадках сила струму I визначається спадом напруги U та опором ділянки R, відповідно до узагальненого закону Ома:
сила струму на кожній ділянці будь-якого кола дорівнює відношенню спаду напруги на цій ділянці до її опору:
|
\(I=\frac{U}{R}\). |
(2.10) |
Розгорнуто
|
$I=\frac{{{\varphi }_{1}}-{{\varphi }_{2}}+\E}{R}$, |
(2.11) |
де φ1– φ2 — різниця потенціалів на кінцях ділянки і $\E$ — ЕРС, яка діє на ній.
За відсутності джерела ($\E$ = 0) спад напруги на ділянці, відповідно до виразу (2.7), збігається з різницею потенціалів на її кінцях. Тож сила струму визначається законом Ома для однорідної ділянки кола:
за відсутності ЕРС сила струму на ділянці кола дорівнює відношенню різниці потенціалів на кінцях до її опору:
|
$I=\frac{{{\varphi }_{1}}-{{\varphi }_{2}}}{R}$. |
(2.12) |
Замкнуте коло теж можна трактувати як ділянку, кінці якої дотикаються. В такому разі у виразі (2.7) φ1 = φ2, і для нерозгалуженого замкненого кола закон Ома набуває вигляду
|
$I=\frac{\E}{R+r}$, |
(2.13) |
де (R + r) – повний опір кола, котрий складається із "навантаження" (зовнішнього опору R) та внутрішнього опору джерела r.
При з'єднанні полюсів джерела напряму (R = 0) по ньому тече струм ''короткого замиканні'')
| $I_{0}=\frac{\E}{r}$. |
(2.13а) |
1.3. З'єднання резисторів і джерел струму
| Основними складовими частинами електричного кола є резистори або опори – елементи, що задовольняють закон Ома і забезпечують потрібний розподіл струмів та напруг у колі. На схемах резистор зображується прямокутником (рис.2.4а) з указанням величини його електричного опору R. В електричних і електронних схемах використовуються також потенціометри – змінні резистори, споряджені двома фіксованими та одним рухомим контактом ("повзунком"), рис. 2.4б.
Потенціометри використовуються для регулювання потенціалів у різних точках кола, або як резистори із змінним опором (реостати) для регулювання струмів на різних ділянках кола. В останньому випадку вони вмикаються в коло одним фіксованим контактом і повзунком. Джерела живлення на схемах теж мають свої позначення, залежні від типу джерела. Зокрема, хімічні джерела (батарейки й акумулятори) зображуються, як показано на рис. 2.5. Відповідно до сказаного, схема найпростішого електричного кола має вигляд рис. 2.6:
Електричні та електронні пристрої, крім найпростіших, містять велику кількість резисторів та інших схемних елементів, які можуть утворювати різноманітні комбінації (з'єднання). Найпростішими з є послідовні та паралельні з'єднання. Параметри цих з'єднань легко визначаються, що дозволяє спростити розрахунок усього кола, розглядаючи кожне з'єднання як один резистор із відповідним опором. Послідовне з'єднання резисторів (рис. 2.7). При такому способі сполучення струм не розгалужується і в усіх резисторах має однакову величину:
|
|
а загальна напруга U0 на кінцях з'єднання дорівнює сумі напруг на кожному з резисторів:
Отже, за законом Ома (2.10) при послідовному з'єднанні резисторів загальний або еквівалентний опір R0 з'єднання дорівнює сумі опорів усіх з'єднаних резисторів:
Зокрема, для n однакових резисторів з опором R
При паралельному з'єднанні (рис. 2.8) є однаковою напруга на резисторах:
|

|
а струм I0 розгалужується по них, так що
За законом Ома (2.10) струм у кожному резисторі \(I_{i}=\frac{U_{0}}{R_{i}}\), отже, загальний струм ${{I}_{0}}={{U}_{0}}\sum\limits_{i=1}^{n}{\frac{1}{{{R}_{i}}}}$. Порівнюючи цей вираз із формулою (2.10), знаходимо співвідношення, що визначає загальний опір паралельного з'єднання резисторів:
При цьому для n резисторів з однаковим опором R виходить
а для двох резисторів із опорами R1, R2
|
На практиці при створенні електричних батарей з потрібними параметрами також використовують з'єднання елементів живлення (рис. 2.9а,б).
|
При послідовному з'єднанні n джерел із ЕРС $\E_{1},\ldots ,\E_{i},\ldots ,\E_{n}$ і внутрішні опори r1, r2,…rn, (рис. 2.9а) загальна ЕРС батареї \(\E_{0}\) дорівнює сумі ЕРС окремих джерел:
а загальний внутрішній опір r0
Якщо всі джерела мають однакові ЕРС (\(\E_{1}=\E_{i}=…=\E_{n}=\E\)) і внутрішні опори (r1 = ... ri = … = rn = r), то
При паралельному з'єднанні джерел (рис. 2.9б) загальний опір r0 і загальна ЕРС \(\E_{0}\) батареї визначаються виразами:
Для однакових джерел (\(\E_{i}=\E\), ri = r)
Якщо батарею замінити одним джерелом із відповідними параметрами \(\E_{0}\) і r0, то струми й напруги в колі залишаться без змін. Тож величини \(\E_{0}\) та r0 називають параметрами еквівалентного джерела. |
1.4. Робота і потужність електричного струму
|
Сили, що забезпечують електричний струм у провіднику, надають носіям енергію електричного струму. Ця енергія неперервно перетворюється на інші види (теплову, світлову, механічну та ін.) і називається ще роботою електричного струму, а інтенсивність її перетворень – потужністю струму. |
|
Робота електричного струму на довільній ділянці кола визначається спадом напруги на ній та перенесеним зарядом, як A = qU. При сталій силі струму І за час t переноситься заряд q = It, тож
і, з урахуванням закону Ома (2.10), для роботи сталого струму на ділянці кола опором R можна записати:
або
|
|
Потужність електричного струму дорівнює роботі струму за одиницю часу й визначається як
Ураховуючи закон Ома (2.10), можна також записати
або
На зовнішній ділянці кола сторонніх сил немає, тож згідно з виразом (2.7), робота струму залежить тільки від різниці потенціалів на клемах джерела. На внутрішній ділянці (всередині джерела) робота струму визначається і кулонівськими, і сторонніми силами. Але, позаяк робота кулонівського поля всередині та поза джерелом є однакова по модулю й протилежна за знаком, то повна робота електричного струму в замкнутому колі визначається тільки сторонніми силами і виконується за рахунок енергії джерела струму:
Відповідно, ця робота за одиницю часу визначає повну потужність струму в замкнутому колі:
Кулонівське поле в колі теж "працює", проте воно не додає струмові енергії, а лише переносить її від джерела до інших ділянок кола.
або
|
1.5. Електроліз
|
Електричний струм у рідинах (електролітах) підпорядковується тим самим загальним законам, що і в твердих провідниках. Але носіями струму в рідинах є не електрони, а іони, тому електричний струм в електролітах супроводжується перенесенням не лише заряду, а й маси (речовини). |
|
При цьому відбуваються специфічні процеси, що називаються електролізом. Зокрема, на опущених в електроліт металевих пластинах-електродах іони-носії струму вступають в окисно-відновні реакції з утворенням нейтральних атомів, або зв'язаних груп атомів. Кількість речовини, що при цьому утворюється, визначають два закони електролізу або закони Фарадея. Перший закон електролізу стверджує:
де коефіцієнт пропорційності k, називається електрохімічним еквівалентом і є табличною характеристикою речовини. Її номінальною мірою є (кг/Кл), але зазвичай використовують (мг/Кл). Вираз (2.29) записують також і через силу струму I в електроліті та час його пропускання t:
Величина k є прямо пов'язана з хімічним еквівалентом $\chi $ – відношенням молярної M (чи атомної А) маси речовини до її валентності n в електроліті. Цей зв'язок виражає другий закон електролізу:
Величина F називається числом або сталою Фарадея. Вона є фунаментальною сталою
(e – елементарний заряд, N0 – стала Авогадро) і дорівнює F = 9,65·104 Кл/моль. Закони Фарадея (2.29) і (2.30) сукупно подають як об'єднаний закон електролізу:
|
Характеристики електричного струму
|
При аналізі характеристик електричного струму носії розглядаються як частинки ідеального газу й використовуються відповідні співвідношення з молекулярно-кінетичної теорії. |
Задача 2.1. Сила електричного струму I у провіднику змінюється з часом t, як показано на графіку I(t). Визначити заряд q, який проходить провідником за перші 5 с.
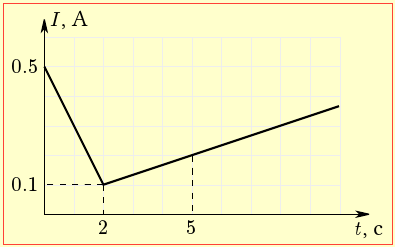
Задача 2.2. За борівською моделлю атома електрон в атомі Гідрогену рухається навколо ядра по коловій орбіті радіуса R = 53 пм. Заряд електрона e = 1,6·10–19 Кл, маса m = 9,1·10–31 кг. Визначити силу еквівалентного струму I, що створюється цим рухом.
Задача 2.3. Густина струму в мідній дротині складає j = 1 А/мм2. Оцінити шлях S, який проходить кожен носій струму за час переміщення уздовж дротини на відстань l = 5 мм при температурі 20°С, прийнявши їхню концентрацію на рівні концентрації атомів.
Задача 2.1
Сила електричного струму I у провіднику змінюється з часом t, як показано на графіку. рис. 1.
Визначити
заряд q, який проходить провідником за перші 5 с.
|
Дано: I(t)
t1 = 0
t2 = 5 c
|
|
q - ?
I0 - ?
|
Розв’язання
При зміні сили струму з часом порція заряду \(\Delta{q_{k}}\), що в якийсь момент tk проходить провідником за малий проміжок часу \(\Delta{t_{k}}\), наближено складає
\(\Delta{q}_{k}\approx{I}(t_{k})\cdot\Delta{t}_{k}\)
і чисельно дорівнює площі відповідної вузької смужки на графіку I(t) шириною Δtk, рис. 1. Відповідно, заряд за весь заданий час наближено визначається сумарною площі таких смужок:
$q\approx \sum\limits_{k}{{{I}_{k}}\Delta {{t}_{k}}}$.
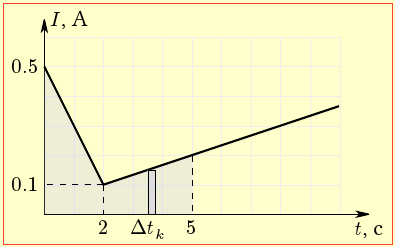
Зрозуміло, що при при зменшенні інтервалів \(\Delta{t_{k}}\) похибка розрахунку зменшується, тож точна величина q чисельно дорівнює площі виділеної ділянки графіка I(t), котра, як видно з рис. 1, утворює з осями координат дві стичні трапеції. Тож, обчисливши їхню сумарну площу за даними умови, дістанемо таку відповідь:
\(q=1,05\) (Кл).
Задача 2.2
За борівською моделлю атома електрон в атомі Гідрогену рухається навколо ядра по коловій орбіті радіуса R = 53 пм (рис. 2). Заряд електрона e = 1,6·10–19 Кл, маса m = 9,1·10–31 кг.
Визначити
силу еквівалентного струму I, що створюється цим рухом.
|
Дано: R = 53 пм = 53·10–12 м
e = 1,6·10–19 Кл
m = 9,1·10–31 кг
|
|
I - ?
|
Розв’язання
 Згідно із завданням, йдеться про величину заряду q, який за одиницю часу переноситься електроном крізь розташовану на його шляху уявну площинку при обертанні навколо ядра. Отже,
Згідно із завданням, йдеться про величину заряду q, який за одиницю часу переноситься електроном крізь розташовану на його шляху уявну площинку при обертанні навколо ядра. Отже,
| I = еn, |
(1) |
де n – частота обертання, тобто кількість обертів електрона по орбіті за 1 с.
Величину n не важко знайти, позаяк вона визначається доцентровим прискоренням ([І], ф-ла (1.28)) електрона, котре дорівнює відношенню сили його притягання до ядра (формула (1.3)) та масою. Тож
| 4π2n2R = $\frac{k{{e}^{2}}}{m{{R}^{2}}}$ $\Rightarrow $ $n=\frac{{{e}}}{2\pi R}\sqrt{\frac{k}{mR}}$. |
|
Відтак за виразом (1) знаходимо відповідь:
$I=\frac{{{e}^{2}}}{2\pi R}\sqrt{\frac{k}{mR}}$,
де k = (1/4πε0) = 9·109 м/Ф.
Обчислення дають:
І = 1,05·10–3 А ≈ 1 мА.
Задача 2.3.
Густина струму в мідній дротині складає j = 1 А/мм2.
Оцінити
шлях S, який проходить кожен носій струму за час переміщення уздовж дротини на відстань l = 5 мм при температурі 20°С, прийнявши їхню концентрацію на рівні концентрації атомів.
|
Дано: j = 1 А/мм2 = 106 А/м2
l = 5 мм = 5·10–3 м
t = 20°С
|
|
S - ?
|
Розв’язання
Упорядкований рух носіїв струму в металах, якими є вільні електрони, відбувається на тлі їхнього хаотичного теплового руху і в певному сенсі нагадує повільне зміщення (дрейф) рою комах під дією легкого вітерцю. Тому швидкість упорядкованого руху носіїв, яку називають дрейфовою швидкістю, є характеристикою не окремих носіїв, а всієї їхньої сукупності. Що ж до поодиноких носіїв, то через хаотичність теплового руху пройдений кожним із них шлях S набагато перевищує зміщення l уздовж провідника і складає
S = vt,
де v – середня швидкість теплового руху носіїв, і t = (l/u) – час їхнього переміщення (дрейфу) вздовж провідника на відстань l із дрейфовою швидкістю u. Отже шуканий шлях
|
\(S=\frac{v}{u}l\). |
(1) |
Дрейфову швидкість u можна визначити з формули (2.4) як
|
\(u=\frac{j}{en}\) |
(2) |
через задані густину струму j і відомий заряд e та концентрацію носіїв n = (N/V), що визначається їхньою кількістю в якомусь виділеному об'ємі провідника.
Величину n можна визначити з основних положень молекулярно-кінетичної теорії ([II], розділ І, п. 1.1). Дійсно, за умовою кількість носіїв у провіднику дорівнює кількості атомів N, отож складає
N = νNА,
де ν (моль) – кількість речовини у провіднику, NА – стала Авогадро (кількість атомів в одному молі). А об'єм
$V=\frac{m}{\rho }=\frac{\nu M}{\rho }$,
де ρ – густина, а m і M – маса виділеної частини провідника та молярна маса його речовини. Отже, для концентрації атомів, тож і носіїв струму, маємо
| $n=\frac{\rho {{N}_{A}}}{M}$. |
(3) |
Відтак за формулою (2) визначаємо дрейфову швидкість u:
|
|
$u=\frac{jM}{e\rho {{N}_{A}}}$, |
(4) |
де e = 1,6·10–19 Кл, NА = 6,02·1023 моль-1, густина міді ρ =(m/V) = 8,9·103 кг/м3, молярна маса M = 64·103 кг/моль. Обчислення дають
u ≈ 10–4 м/с = 0,1 мм/с.
Швидкість теплового руху носіїв (електронів) оцінимо за формулою середньоквадратичної швидкості частинок ідеального газу ([ІІ], ф-ла (1.9)):
\(v\approx\sqrt{\frac{3kT}{m}}\),
де k = 1,38·10-23 Дж/К – стала Больцмана, m = 9,1·10-31 кг – маса електрона, T = 293 К (20 °С). Тож
v ≈ 105 м/с.
Відтак, за отриманими значеннями v i u з формули (1) знайдемо наступну оцінку шляху, який проходить окремий носій за час дрейфу уздовж провідника на відстань l = 5 мм:
S ≈ 5000 км.
Отже, цей вражаючий результат свідчить, що спрощене уявлення про рух носіїв струму вздовж провідника зі струмом є вельми умовним.
Електричний опір. З'єднання резисторів
Перш ніж розглядати наведені приклади варто уважно прочитати рекомендації по розв'язуванню задач цього типу.
Задача 2.4. Визначити довжину та діаметр намотаного на котушку мідного дроту масою 28 г і опором 54,1 Ом. Густина міді D = 8900 кг/м3, питомий опір ρ = 17 нОм·м.
Задача 2.5. Плоский конденсатор ємністю C = 100 пФ заповнено діелектриком із проникністю \(\varepsilon=2,1\) і питомим опором \(\rho\) = 1010 Ом·м. Визначити силу струму через конденсатор (струм ''витоку'') при напрузі U = 100 В.
Задача 2.6. Графітовий та залізний стрижні однакового перерізу з'єднують послідовно. Визначити, при якому відношенні довжин сумарний електричний опір стрижнів не залежатиме від температури. Термічний коефіцієнт опору графіту α1 = –0,8·10–3 K–1; заліза α2 = 6·10–3 K–1; відповідні питомі опори \(\rho_{1}= 40\) мкОм·м і \(\rho_{2}= 0,12\) мкОм·м.
Задача 2.7. При пропусканні через електричну лампу струму I1 = 4 мА при початковій температурі t1 = 20 °C напруга на вольфрамовій нитці розжарювання складає U1 = 100 мВ. Визначити робочу температуру нитки t2 при напрузі U2 = 220 В і струмі I2 = 0,7 A. Термічний коефіцієнт опору вольфраму α = 4,8·10–3 K–1.
Задача 2.8. Електричний опір послідовного з'єднання двох резисторів дорівнює R01 = 8 Ом, а паралельного R02 = 1,5 Ом. Визначити опір кожного резистора.
Задача 2.9. Потенціометр із повним опором R0 включено в електричне коло в точках a і b, як показано на рис.9. Показати графік залежності опору R всього потенціометра між точками a і b від опору r його правої частини.
Задача 2.10. Визначити опір Rab між вершинами a-b сітки, виготовленої з дротин однакового опору R (рис.10).
Задача 2.4
Визначити
довжину та діаметр намотаного на котушку мідного дроту, якщо його маса 28 г і електричний опір 54,1 Ом. Густина міді D = 8,9·103 кг/м3, питомий опір ρ =17 нОм·м.
|
Дано: m = 28 г R = 54,1 Ом
D = 8,9·103 кг/м3
ρ =17 нОм·м
|
|
l – ? d – ?
|
Розв’язання
Електричний опір і маса провідника відомими співвідношеннями пов'язані з розмірами (рис. 4) та відповідними характеристиками речовини:
співвідношеннями пов'язані з розмірами (рис. 4) та відповідними характеристиками речовини:
|
\(R=\frac{\rho}{l}S\); |
(1) |
|
\(m = D{V}=D{S}{l}\). |
(2) |
Тож, почленно помноживши ці вирази, отримаємо довжину
$l=\sqrt{\frac{Rm}{\rho D}}$ = 100 м,
а поділивши – площу поперечного перерізу дроту:
$S=\sqrt{\frac{\rho m}{DR}}$ = 3,14·10–2 мм2
і відтак – його діаметр:
$d=2\sqrt{\frac{S}{\pi }}$= 0,2 мм.
Задача 2.5
Плоский конденсатор ємністю C = 100 пФ заповнено діелектриком із проникністю \(\varepsilon=2,1\) і питомим опором \(\rho\) = 1010 Ом·м.
Визначити
силу струму через конденсатор (струм ''витоку'') при напрузі U = 100 В.
|
Дано: C = 100 пФ = 10–10 Ф
\(\varepsilon=2,1\)
\(\rho\) = 1010 Ом·м
|
|
І – ?
|
Розв’язання
Будь-який реальний діелектрик має хоча й дуже великий, але скінченний питомий опір. Тому через конденсатор, що перебуває під напругою, протікає певний "струм витоку". Тож у контексті задачі конденсатор є провідником із заданим питомим опором \(\rho\) певним перерізом S (площею обкладок), довжиною d (відстанню між ними, рис.5)

і відповідним опором (формула (2.8))
|
\(R=\rho\frac{d}{S}\). |
|
За формулою (1.24) відношення (d/S) дорівнює
\(\frac{d}{S}=\frac{\varepsilon\varepsilon_{0}}{C}\),
отже,
\(R=\rho\frac{\varepsilon\varepsilon_0}{C}\).
Згідно з даними умови та значенням\(\varepsilon_{0}=8,85\cdot{10}^{-12}\) Ф/м, це дає наступну числову відповідь:
R = 1,86·109 Ом = 1,86 ГОм,
тож струм витоку, за законом Ома (2.10), дорівнює
І ≈ 5,4·10–8 А = 54 нА.
Задача 2.6.
Графітовий та залізний стрижні однакового перерізу з'єднують послідовно.
Визначити,
при якому відношенні довжин сумарний електричний опір стрижнів не залежатиме від температури. Термічний коефіцієнт опору графіту α1 = –0,8·10–3 K–1, заліза α2 = 6·10–3 K–1; відповідні питомі опори \(\rho_{1}= 40\) мкОм·м і \(\rho_{2}= 0,12\) мкОм·м.
|
Дано: α2 =–0,8·10–3 K–1 α2 = 6·10–3 K–1 ρ1 = 4·10–5 Ом·м ρ2 = 1,2·10–7 Ом·м |
|
l2/l1 - ?
|
Розв’язання
Температурна залежність опору обох стрижнів визначається однією формулою (2.9а). Але, позаяк α1 і α2 мають різний знак, опори стрижнів змінюються в протилежному напрямку: якщо в одному опір зростає, то в іншому зменшується і навпаки. Через це за відповідних умов у з’єднаних стрижнях вказані зміни можуть компенсуватись.
При послідовному з'єднанні резисторів опори додаються (формула (2.15)), отже, згідно з виразом (2.9а), загальний опір стрижнів R при довільній температурі t складає:
\(R=R_{1}+R_{2}=R_{01}(1+\alpha_{1}t)+R_{02}(1+\alpha_{2}t)\) =
=\((R_{01}+R_{02})+(R_{01}\alpha_{1}+R_{02}\alpha_{2})t\),
де R01, R02 – опори при t = 0 °C. Звідси випливає, що величина R не залежатиме від температури, якщо
\((R_{01}\alpha_{1}+R_{02}\alpha_{2})t=0\) \(\Rightarrow\) \(R_{01}\alpha_{1}=-R_{02}\alpha_{2}\) \(\Rightarrow\) \(\frac{R_{01}}{R_{02}}=-\frac{\alpha_{2}}{\alpha_{1}}\).
З отриманого співвідношення, взявши до уваги однаковість перерізів стрижнів і формулу (2.8), знайдемо відповідь:
\(\frac{l_{2}}{l_{1}} = –\frac{\rho_{1}\alpha_{1}}{\rho_{2}\alpha_{2}}\) ≈ 44.
Варто зауважити, що такий принцип іноді використовують для нівелювання температурної залежності параметрів прецизійних електровимірювальних приладів.
Задача 2.7
При пропусканні через електричну лампу струму I1 = 4 мА при робочій температурі t1 = 20 °C напруга на вольфрамовій нитці розжарювання складає U1 = 100 мВ.
Визначити
робочу температуру нитки t2 при напрузі U2 = 220 В і струмі I2 = 0,7 A. Термічний коефіцієнт опору вольфраму α = 4,8·10–3 K-1.
|
Дано: \(t_{1}=27\) °C
\(I_{1}=4\) мА
\(U_{1}=100\) мВ
\(I_{2}=0,7\) A
\(U_{2}=220\) В
\(\alpha=4,8\cdot{10}^{-3}\) K-1
|
|
\(t_{2}\) - ?
|
Розв’язання
За законом Ома (2.10) указані в умові струми та напруги по суті задають значення R1 і R2 опору нитки розжарювання лампи, відповідно, при початковій t1 і шуканій робочій температурі t2:
R1 = 25 Ом; R1 = 314,3 Ом.
Отже, згідно з виразом (2.9а), можна записати
$\frac{{{R}_{2}}}{{{R}_{1}}}=\frac{1+\alpha {{t}_{2}}}{1+\alpha {{t}_{1}}}$
і після простих перетворень отримати відповідь задачі:
|
$ {{t}_{2}}=\frac{{{R}_{2}}\left( 1+\alpha {{t}_{1}} \right)-{{R}_{1}}}{\alpha {{R}_{1}}}$t2 ≈ 2660°C. |
(1) |
Наведений розв'язок ілюструє метод вимірювання температури, що зветься "термометром опору" й дозволяє вимірювати високі та низькі температури в діапазонах, які є недоступні для традиційних рідинних термометрів. При цьому для визначення температури якогось об'єкта із ним приводять у контакт і вимірюють опір R датчика – резистора із відомими значеннями R0 і α. У такому разі за виразом (1) вимірювана температура дорівнює
|
$t=\frac{n-1}{\alpha }$, |
(2) |
де n = (R/R0).
Задача 2.8. Електричний опір послідовного з'єднання двох резисторів дорівнює R01 = 8 Ом, а паралельного R02 = 1,5 Ом.
Визначити
опір кожного резистора.
|
Дано: R01 = 8 Ом R02 = 1,5 Ом |
|
R1 –? R2 –? |
Розв’язання
Якщо позначити опір одного з резисторів як R, то при послідовному з'єднанні (формула 2.15) опір іншого складе R01– R. Отже, для паралельного з"єднання (формула (2.1а)) маємо:
$\frac{R\left( {{R}_{01}}-R \right)}{{{R}_{01}}}={{R}_{02}}$ $\Rightarrow $ ${{R}^{2}}-{{R}_{01}}R+{{R}_{01}}{{R}_{02}}=0$
або в числах
${{R}^{2}}-8R+12=0$.
Корені цього рівняння дорівнюють
R1 = 6 Ом; R2 = 2 Ом
і є відповідями задачі.
Задача 2.9
Потенціометр із повним опором R0 включено в електричне коло в точках a і b, як показано на рис.9.
Показати
графік залежності опору R всього потенціометра між точками a і b від опору r його правої частини.
|
Дано: R0
|
|
R(r) – ?
|
Розв’язання
Потенціометр являє собою резистор, споряджений ковзним контактом а (повзунком), що залежно від способу включення дозволяє регулювати або струм, або напругу на інших ділянках кола.
Як зрозуміло з рис. 9 і 9-1 а-в, повзунок ділить опір потенціометра на дві паралельно з'єднані частини з опорами r і (R0 – r). Отже, за формулою (2.16б) загальний опір між точками а і b в залежності від r складає
$R\left( r \right)=\frac{r\left( {{R}_{0}}-r \right)}{{{R}_{0}}}$.
На графіку ця залежність зображується параболою з максимумом Rm = (R0/4), як показано на рис.9-1 г

З приводу отриманого результату слід зауважити таке. Графік R(r) наочно показує, що після проходження повзунка через середнє положення величина R у зворотньому порядку набуває всіх попередніх значень. Тому розглянуте включення потенціометра в коло реально не має сенсу і на практиці не використовується.
Задача 2.10
Визначити
опір Rab між вершинами a-b сітки, виготовленої з дротин однакового опору R (рис.10).
Дано:
|
R
|
|
R0 -?
|
Розв’язання
Сітка являє собою з'єднання 12 однакових резисторів R (рис. 10-1а), котре не є ані паралельним, ані послідовним, отже, знайти відповідь безпосередньо за формулами (2.15), або (2.16) неможливо. Але задачу спрощує симетрія електричної схеми сітки, через що струми в симетричних гілках і потенціали симетричних вузлів збігаються. Тож не важко збагнути, що з'єднання, або роз'єднання гілок у таких точках не вплине на розподіл струмів і потенціалів, тому при розрахунках сітку можна замінити більш простою еквівалентною схемою. Далі розглянуто дві такі можливості.
1. Якщо попарно з'єднати всі симетричні відносно діагоналі a-b вузли (рис. 10-1б), а потім за формулами (2.15а) та (2.16а) поступово ''згорнути'' отриману схему, як показано на рис.10-1в-д, то врешті дістанемо одну еквівалентну гілку (рис. 10е) і наступну відповідь:
R0 = 1,5R.
2. Розірвавши схему в т. f, отримаємо вихідну еквівалентну схему рис. 10-2а і чинячи, як раніше (рис. 10-2 б-в), дістанемо ту саму відповідь.
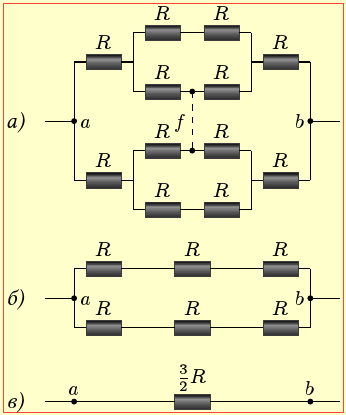
На завершення зауважимо, що розглянутий ланцюг є симетричним лише в електричному сенсі й реально зовсім не має складатися з геометрично упорядкованих однакових дротяних квадратиків.
Закон Ома
Задача 2.11. Визначити відносну похибку ε виміру напруги на резисторі R = 10 Ом вольтметром із власним опором RV = 100 Ом.
Задача 2.12. Визначити додатковий опір RД, який треба підключити до вольтметра із власним опором RV = 10 кОм, аби розширити його діапазон вимірювань у n = 10 разів.
Задача 2.13. Визначити опір резистора (шунта) Rш, який слід приєднати до амперметра із власним опором RA = 0,6 Ом, аби розширити діапазон вимірювань у n = 10 разів.
Задача 2.14. Напруга на кінцях заданого ланцюжка (рис. 14) UАВ = 10 В, а опори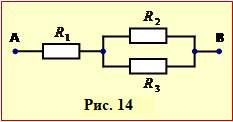 резисторів R1 = 3,5 Ом, R2 = 2 Ом, R3 = 6 Ом. Визначити струми I1, I2, I3 та напруги U1, U2, U3 на всіх резисторах.
резисторів R1 = 3,5 Ом, R2 = 2 Ом, R3 = 6 Ом. Визначити струми I1, I2, I3 та напруги U1, U2, U3 на всіх резисторах.
Задача 2.15. Резистор з опором R = 10 Ом і невідомий резистор Rx, що з’єднані між собою один раз послідовно, а інший паралельно, підключають до джерела із внутрішнім опором r = 2 Ом. Визначити опір Rx невідомого резистора, якщо в обох випадках струм у ньому однаковий.
Задача 2.16. Струм у підключеному до джерела резисторі R1 = 2 Ом складає I1 = 5 А, а напруга на підключеному натомість резисторі R2 = 120 Ом U2 = 12 В. Знайти струм короткого замикання джерела I0.
Задача 2.17. Два джерела з ЕРС і внутрішніми опорами ${{\E}_{1}}$ = 2 В, r1 = 0,4 Ом та ${{\E}_{2}}$ = 1,5 В, r2 = 0,6 Ом з’єднан0 однойменними полюсами. Визначити різницю потенціалів на клемах Δφ і силу струму в джерелах I.
Задача 2.18. Два ідеальні (без внутрішнього опору) джерела ${{\E}_{1}}$ = 4,5 В, ${{\E}_{2}}$= 2В і три резистори R1 = 1,5 Ом, R2 = 1 Ом, R = 4 Ом, є з'єднані, як показано на рис.18. Визначити величину і напрям струму в кожному резисторі.
${{\E}_{2}}$= 2В і три резистори R1 = 1,5 Ом, R2 = 1 Ом, R = 4 Ом, є з'єднані, як показано на рис.18. Визначити величину і напрям струму в кожному резисторі.
Задача 2.11
Визначити
відносну похибку ε виміру напруги на резисторі R = 10 Ом вольтметром із власним опором RV = 100 Ом.
|
Дано: R = 10 Ом RV = 100 Ом
|
|
ε - ?
|
Розв'язання
Вольтметр підключається до резистора паралельно і показує напругу на утвореному ланцюжку (рис. 11) опором (формула 2.16а)
|
${{R}_{0}}=\frac{{{R}_{V}}R}{{{R}_{V}}+R}$ |
(1) |
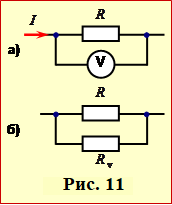 Тож виміряна UV та істинна U напруги за законом Ома (2.10) дорівнюють UV = IR0 і U = IR, де І – струм у підвідних проводах, який уважатимемо незмінним. Отже, відносна похибка виміру
Тож виміряна UV та істинна U напруги за законом Ома (2.10) дорівнюють UV = IR0 і U = IR, де І – струм у підвідних проводах, який уважатимемо незмінним. Отже, відносна похибка виміру
$\varepsilon =\frac{U-{{U}_{V}}}{U}$ = $\frac{R-{{R}_{0}}}{R}$
і, з урахуванням виразу (1), складає
|
$\varepsilon =\frac{{{R}}}{{{R}_{V}}+R}$ ≈ 9 %. |
(2) |
З приводу отриманого результату слід зробити два зауваження.
1.Теоретично струми в проводах до і після підключення вольтметра мають відрізнятися через зміну опору даної ділянки кола. Але спричинена цим можлива зміна струму є настільки незначною, що не вартує уваги.
2. Як видно з виразу (2), для забезпечення достатньої точності вимірів вольтметр має мати доволі великий власний опір. До прикладу, при допустимій похибці ε ≤ 1% має бути RV ≥ 100R. Тому для прецизійних (надточних) вимірювань використовують інші, непрямі методи визначення напруги.
Задача 2.12
Визначити
додатковий опір RД, який треба підключити до вольтметра із власним опором RV = 10 кОм, аби розширити його діапазон вимірювань у n = 10 разів.
|
Дано: RV = 10 кОм
n = 10
|
|
RД - ?
|
Розв’язання
Кожен вольтметр може безпосередньо вимірювати лише напруги, котрі не перевищують певної величини Um, яка визначає його діапазон вимірювань (шкалу). Але шкалу вольтметра можна розширити, якщо безпосередньо подавати на нього не всю вимірювану напругу, а тільки її визначену частку. Для цього до вольтметра послідовно підключають додатковий опір ("добавку") – резистор із заданим опором RД (рис.12).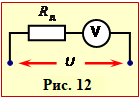
Необхідну величину RД легко розрахувати. Позаяк струм у складових ланцюжка вольтметр-добавка однаковий, то відповідно до закону Ома (2.10),
$\frac{U}{{{U}_{V}}}=\frac{{{R}_{}}+{{R}_{V}}}{{{R}_{V}}}$ $\Rightarrow $ ${{R}_{Д}}={{R}_{V}}\left( \frac{U}{{{U}_{V}}}-1 \right)$,
де U – подана напруга, і UV, RV – напруга на вольтметрі та його власний опір.
За умовою при UV = Um подана напруга U має дорівнювати nUm, отже
для розширення шкали вольтметра в n разів до нього треба послідовно підключити додатковий опір
RД = (n – 1)RV,
який, згідно з даними умови, дорівнює 90 кОм.
Задача 2.13
Визначити
опір резистора (шунта) Rш, який слід приєднати до амперметра із власним опором RA = 0,6 Ом, аби розширити діапазон вимірювань у n = 10 разів.
.
|
Дано: RA = 0,9 Ом
n = 10
|
|
Rш - ?
|
Розв’язання
За змістом і логікою розв'язування дана задача є аналогом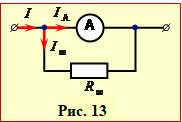 попередньої. А саме, для розширення діапазону вимірювань (шкали) до амперметра паралельно підключають "шунт" – резистор із заданим опором Rш (рис. 13),– за допомогою котрого від амперметра відгалужують надлишковий струм величиною
попередньої. А саме, для розширення діапазону вимірювань (шкали) до амперметра паралельно підключають "шунт" – резистор із заданим опором Rш (рис. 13),– за допомогою котрого від амперметра відгалужують надлишковий струм величиною
\(I_{ш}=I-I_{А}\),
де І – вимірюваний струм, ІА – струм, що проходить через амперметр. За умовою І = nІА, отже,
Іш = (n–1)ІА,
і, позаяк напруга на амперметрі та шунті однакова, відповідно до закону Ома (2.10),
для розширення шкали амперметра в n разів до нього треба паралельно підключити шунт опором
${{R}_{ш}}=\frac{{{R}_{A}}}{n-1}$.
За умовою n = 10, отже, відповідь
Rш = 0,1 Ом.
Задача 2.14
 Напруга на кінцях заданого ланцюжка (рис. 14) UАВ = 10 В, а опори резисторів R1 = 3,5 Ом, R2 = 2 Ом, R3 = 6 Ом.
Напруга на кінцях заданого ланцюжка (рис. 14) UАВ = 10 В, а опори резисторів R1 = 3,5 Ом, R2 = 2 Ом, R3 = 6 Ом.
Визначити
струми I1, I2, I3 та напруги U1, U2, U3 на всіх резисторах.
|
Дано: UAB = 10 В
R1 = 3,5 Ом
R2 = 2 Ом
R3 = 6 Ом
|
|
I1, I2, I3 - ?
U1, U2, U3 - ?
|
Розв’язання
Замінимо у початковій схемі резистори R2, R3 на один еквівалентний з опором R23 (формула (2.16а))
|
\(R_{23}=\frac{R_{2}R_{3}}{ R_{2}+R_{3}}=1,5\ {Ом}\) |
(1) |
отримаємо послідовне з’єднання резисторів R23 і R1 (рис.14-1) із загальним опором R0 = R23 + R1, напруга на якому дорівнює UAB. Отже, за законом Ома (2.10) загальний струм у ланцюжку, тож у резисторі R1, струм дорівнює
\(I_{0}=I_{1}=\frac{U}{R_{0}}=\frac{U}{R_{23}+R_{1}}=2\ {А}\),
і напруга
\(U_{1}=I_{0}R_{1}=7\ {В}\),
Відповідно, напруга на резисторах R2 і R3 дорівнює
|
\(U_{23}= U_{АВ}-U_{1}=3\ {В}\), |
(2) |
а струми становлять
|
|
\(I_{2}=\frac{U_{23}}{R_{2}}=1,5\ {А}\); \(I_{3}=\frac{U_{23}}{R_{3}}=0,5\ {А}\). |
|
Враховуючи співвідношення (2) і формулу (1) вирази струмів I2, I3 можна переписати, як
\(I_{2}=I_{0}\frac{R_{3}}{R_{2}+R_{3}}\);
\(I_{3}=I_{0}\frac{R_{2}}{R_{2}+R_{3}}\).
і сформулювати наступний алгоритм обчислення:
при паралельному з’єднанні двох резисторів струм в одному дорівнює загальному струмові, помноженому на опір іншого й поділеному на їхній сумарний опір.
”Інший” резистор називається ”стороннім опором”, а сформульований рецепт обчислення – ”правилом стороннього опору” і використовується в електротехніці при практичних розрахунках.
Задача 2.15
Резистор опором R = 10 Ом і невідомий резистор Rx, що з’єднані між собою один раз послідовно, а інший паралельно, підключають до джерела із внутрішнім опором r = 2 Ом.
Визначити
опір Rx невідомого резистора, якщо в обох випадках струм у ньому однаковий.
|
Дано: r = 2 Ом
R = 10 Ом
|
|
Rx - ?
|
Розв’язання
Якщо позначити загальний опір підключених до джерела резисторів при послідовному з'єднанні (рис.15а) як R1, і при паралельному (рис.15б) як R2, а сили струму як І1 й І2, то за законом Ома (2.13)
|
${{I}_{1}}=\frac{\E}{{{R}_{1}}+r}$; ${{I}_{2}}=\frac{\E}{{{R}_{2}}+r}$. |
(1) |
За умовою струм через резистор Rx у другому випадку є такий самий як і в першому, тобто І1. Отже за розглянутим у попередній задачі "правилом стороннього опору" можна записати:
|
${{I}_{1}}={{I}_{2}}\frac{R}{{{R}_{1}}}$ $\Rightarrow $ $\frac{{{I}_{2}}}{{{I}_{1}}}=\frac{{{R}_{1}}}{R}$ |
|
і, почленно поділивши вирази (1),
|
$\frac{{{R}_{1}}}{R}=\frac{{{R}_{1}}+r}{{{R}_{2}}+r}$. |
(2) |
Відтак, зробивши в цьому виразі підстановки
${{R}_{1}}=R+{{R}_{x}}$;
${{R}_{2}}=\frac{R{{R}_{x}}}{R+{{R}_{x}}}$.
й розв'язавши отримане рівняння, дістанемо наступну відповідь:
\(R_{x}=\frac{R^{2}}{r}=50\) Ом.
(Вказівка. При розв'язуванні рівняння варто ввести заміну Rх = ηR і шукати параметр η).
Задача 2.16
Струм у підключеному до джерела резисторі R1 = 2 Ом складає I1 = 5 А, а напруга на підключеному натомість резисторі R2 = 120 Ом U2 = 12 В.
Визначити
струм короткого замикання джерела I0.
|
Дано: R1 = 2 Ом
I1 = 5 А
R2 = 120 Ом
U2 = 12 В
|
|
I0 - ?
|
Розв’язання
Струмом короткого замикання джерела називається струм, який виникає при його "закорочуванні", тобто з'єднанні полюсів дротом із гранично малим опором R = 0. Отже, за законом Ома (2.13) маємо:
|
|
${{I}_{0}}=\frac{\E}{r}$ |
(1) |
де \(\E\) і r – ЕРС і внутрішній опір джерела.
Так само, відповідно до виразів закону Ома (2.13) і (2.7), можна скласти систему рівнянь
|
$\begin{align} & {{I}_{1}}=\frac{\E}{{{R}_{1}}+r} \\ & {{U}_{2}}=\frac{\E}{{{R}_{1}}+r}{{R}_{2}} \\ \end{align}$ |
(2) |
і знайти величини $\E$ та r, а відтак за формулою (1) – шуканий струм короткого замикання I0. Але, позаяк у рівняннях (2) опір джерела r є "зав'язаний" на опори R1, R2, визначення величин $\E$ та r порізно прямими підстановками потребує громіздких викладок. Проте струм I0 можна знайти одразу, застосовувати наступний штучний спосіб.
Перепишемо вираз (1) і рівняння (2) в "перевернутому" вигляді й, зробивши підстановку
\(\frac{r}{\E}=\frac{1}{{{I}_{0}}}\),
отримаємо:
$\begin{align} & \frac{1}{{{I}_{1}}}-\frac{1}{{{I}_{0}}}=\frac{{{R}_{1}}}{\E} \\ & \frac{1}{{{U}_{2}}}-\frac{1}{{{I}_{0}}{{R}_{2}}}=\frac{1}{\E} \\ \end{align} $.
Відтак, почленно помноживжи друге рівняння на R1 та прирівнявши праві частини, легко отримаємо наступну загальну відповідь
${{I}_{0}}=\frac{{{I}_{1}}{{U}_{2}}\left( {{R}_{2}}-{{R}_{1}} \right)}{\left( {{U}_{2}}-{{I}_{1}}{{R}_{1}} \right){{R}_{2}}}$
та числове значення
I0 = 29,5 А.
Задача 2.17
Два джерела з ЕРС і внутрішніми опорами ${{\E}_{1}}$=2 В, \(r_{1}= 0,4\) Ом та ${{\E}_{2}}$= 1,5 В, \(r_{2}=0,6\) Ом з’єднан0 однойменними полюсами.
Визначити
різницю потенціалів на клемах Δφ і силу струму в джерелах I.
|
Дано: ${{\E}_{1}}$ = 2В ${{\E}_{2}}$=1,5В r1 = 0,4 Ом r2 = 0,6 Ом |
|
Δφ-?, I -?
|
Розв’язання
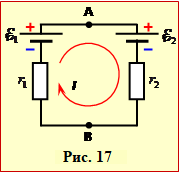 Джерела утворюють нерозгалужене коло (рис. 17) з двох ділянок А-В і В-А, з однаковим струмом I1 = I2 = І. Тож, увівши позначення φА – φВ = Δφ, за законом Ома (2.10) і виразом (2.7) маємо:
Джерела утворюють нерозгалужене коло (рис. 17) з двох ділянок А-В і В-А, з однаковим струмом I1 = I2 = І. Тож, увівши позначення φА – φВ = Δφ, за законом Ома (2.10) і виразом (2.7) маємо:
|
$\frac{-\Delta \varphi +{{\E}_{1}}}{{{r}_{1}}}=\frac{\Delta \varphi -{{\E}_{2}}}{{{r}_{2}}}\quad \Rightarrow \quad \Delta \varphi =\frac{{{\E}_{1}}{{r}_{2}}+{{\E}_{2}}{{r}_{1}}}{{{r}_{1}}+{{r}_{2}}}$ = 1,8 В. |
(1) |
|
І = 0,5 А. |
|
Отримані відповіді можна знайти й дещо інакше. А саме.
Указані джерела сполучені однойменними полюсами й утворюють батарею, до якої не підключено навантаження. Тож різниця потенціалів Δφ на полюсах А і В збігається з ЕРС і визначається формулами (2.20) і (2.21):
$\Delta \varphi =\frac{{{r}_{1}}{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}}\left( \frac{{{\E}_{1}}}{{{r}_{1}}}+\frac{{{\E}_{2}}}{{{r}_{2}}} \right)=\frac{{{\E}_{1}}{{r}_{2}}+{{\E}_{2}}{{r}_{1}}}{{{r}_{1}}+{{r}_{2}}}$ = 1,8 В.
Величину струму І теж можна визначити альтернативно, розглядаючи джерела як замкнене коло із загальною ЕРС $\E$ = ${{\E}_{1}}$– ${{\E}_{2}}$ і опором r = r1 + r2. У такому разі за законом Ома
$I=\frac{{{\E}_{1}}-{{\E}_{2}}}{{{r}_{1}}+{{r}_{2}}}$ = 0,5 А.
На завершення варто зауважити таке. Знайдений струм розряджає указані джерела, навіть коли вони не підключені до зовнішнього кола. Тому реально в батареї з'єднують тільки ідентичні елементи живлення, для яких І = 0.
Задача 2.18
Два ідеальні (без внутрішнього опору) джерела ${{\E}_{1}}$=4,5В, ${{\E}_{2}}$=2В і три резистори R1 = 1,5 Ом, R2 = 1 Ом, R = 4 Ом, є з'єднані, як показано на рис.18.
три резистори R1 = 1,5 Ом, R2 = 1 Ом, R = 4 Ом, є з'єднані, як показано на рис.18.
Визначити
величину і напрям струму в кожному резисторі.
|
Дано: ${{\E}_{1}}$ = 4,5 В, ${{\E}_{2}}$= 2ВR1 = 1,5 Ом R2 = 1 Ом R = 4 Ом |
|
I, I1, I2 - ?
|
Розв’язання
Напрямки шуканих струмів, які показано на рис. 18-1, фактично є очевидними. При заданій полярності джерел φА > φВ, отже, в резисторі R струм іде від А до В. А, з огляду на величини ЕРС, напрям струму в джерелах є такий, як у попередній задачі, бо через відсутність сторонніх сил у резисторі R він не впливає на напрямки струмів .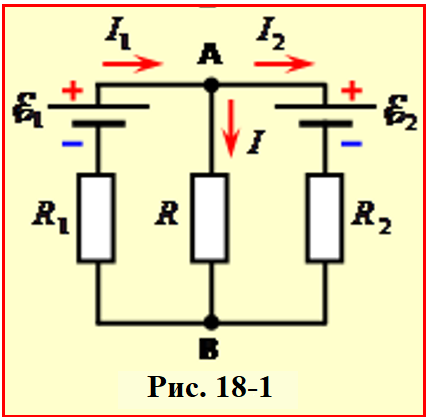
Що ж до величини струмів, то вона визначається законом Ома (2.12) для резистора R і (2.11) для R1 та R2 . Окрім того, за законом збереження заряду струм І1 в т. А розгалужується на І та І2 без зміни їхньої сумарної величини. Тож у відповідності із сказаним можна скласти наступну систему рівнянь:
|
${{I}_{1}}{{R}_{1}}={{\varphi }_{B}}-{{\varphi }_{A}}+{{\E}_{1}}$; ${{I}_{2}}{{R}_{2}}={{\varphi }_{A}}-{{\varphi }_{B}}-{{\E}_{2}}$; ${I}{R} ={{\varphi }_{A}}-{{\varphi }_{B}}$ ${{I}_{1}} =I+{{I}_{2}}$. |
|
${{I}_{1}}=\frac{{{\E}_{1}}\left( R+{{R}_{2}} \right)-{{\E}_{2}}R}{R{{R}_{1}}+{{R}_{1}}{{R}_{2}}+{{R}_{2}}R}$ = 1,26 A;
${{I}_{2}}=\frac{{{-\E}_{2}}\left( R+{{R}_{1}} \right)+{{\E}_{1}}R}{R{{R}_{1}}+{{R}_{1}}{{R}_{2}}+{{R}_{2}}R}$ = 0,61 A;
$I=\frac{{{\E}_{1}}{{R}_{2}}+{{\E}_{2}}{{R}_{1}}}{R{{R}_{1}}+{{R}_{1}}{{R}_{2}}+{{R}_{2}}R}$ = 0,65 A.
Робота і потужність струму
Задача 2.19. До джерела з ЕРС ${{\E}}$ = 10 В і внутрішнім опором r = 2 Ом підключено реостат із дуже великим загальним опором. А) Показати графіки залежності корисної потужності P(R) і ККД джерела η(R) від опору реостата R. Б) Визначити, при якій величині Rm та з яким ККД ηm джерело віддає в навантаження максимальну потужність і чому дорівнює її величина Pm.
Задача 2.20. У резисторі опором R = 9 Ом, який підключено до джерела з ЕРС ${{\E}_{1}}$ = 10 В, виділяється \(\eta=\) 90 % повної потужності джерела. Визначити максимальну корисну потужність Pm, яку можна отримати від цього джерела.
Задача 2.21. При почерговому підключенні резисторів R1 = 4 Ом і R2 = 9 Ом до акумуляторної батареї через деякий баластний опір R0 на кожному з резисторів виділяється потужність P = 36 Вт. Нехтуючи внутрішнім опором, визначити ЕРС батареї ${{\E}}$ та струм І0 через неї при замиканні безпосередньо на баластний опір.
Задача 2.22. Споживач, який знаходиться на відстані l = 7,5 км від генератора, отримує потужність P = 100 кВт. Визначити масу m мідного дроту двопровідної лінії живлення споживача, якщо напруга на вході дорівнює U0 = 6 кВ і втрати потужності в лінії складають k = 3 %.
Задача 2.23. Трамвай масою m = 50 т спускається зі швидкістю v = 36 км/год по колії з ухилом \(\alpha=0,01\) і коефіцієнтом опору \(\mu=0,03\). Визначити струм I в обмотці двигуна трамваю, якщо напруга в контактній мережі U = 500 В і ККД двигуна \(\eta=0,8\).
Задача 2.24. Ніхромовим (питомий опір \(\rho=1\) мкОм·м) дротом діаметром d = 0,4 мм треба намотати нагрівник, який при напрузі U = 220 В і ККД \(\eta=\) 40 % за час \(\tau=10\) хв доводить до кипіння V = 1 л води (питома теплоємність c = 4200 Дж/(кг·К)) із початковою температурою t = 20 °C. Визначити необхідну довжину дроту l.
Задача 2.25. Нагрівник електричного чайника складається з двох секцій. Визначити, за який час t0 у чайнику закипить однакова кількість води з однаковою початковою температурою при а) послідовному і б) паралельному сполученні секцій, якщо при їхньому почерговому ввімкненні цей час складає t1 = 10 хв і t2 = 40 хв, відповідно.
Задача 2.19
До джерела з ЕРС ${{\E}}$ = 10 В і внутрішнім опором r = 2 Ом підключено реостат із дуже великим загальним опором.
А) Показати графіки залежності корисної потужності P(R) і ККД джерела η(R) від опору реостата (навантаження) R.
Б) Визначити, при якій величині Rm та з яким ККД ηm джерело віддає в навантаження максимальну потужність і чому дорівнює її величина Pm.
Дано:
|
${{\E}_{1}}$ = 10 В
r = 2 Ом
|
|
P (R)-?, \(\eta{(R)}\)-?
Pm - ?,\(\eta_{m}\) - ?
|
Розв’язання
 А. Підключений до джерела реостат (рис. 19), або якийсь інший пристрій з відповідним опором R називають навантаженням, а потужність P, що виділяється в ньому, – корисною потужністю джерела. Отже, згідно з формулою (2.24) і законом Ома (2.13), корисна потужність
А. Підключений до джерела реостат (рис. 19), або якийсь інший пристрій з відповідним опором R називають навантаженням, а потужність P, що виділяється в ньому, – корисною потужністю джерела. Отже, згідно з формулою (2.24) і законом Ома (2.13), корисна потужність
|
\(P=\frac{{\E}^{2}R}{(R+r)^{2}}\). |
(1) |

Із цього виразу випливає, що при R << r
\(P≈\frac{{\E}^{2}R}{r^{2}}\),
а при R >> r
\(P≈\frac{{\E}^{2}}{R}\).
Отже, при поступовому збільшенні величини R корисна потужність спочатку зростає, а потім зменшується, так що при певному навантаженні R = Rm набуває максимальної величини P = Pm, як показано на графіку P (R), рис 19-1.
Повна потужність струму в колі визначається формулою (2.26), а ККД джерела – формулою (2.28):
$\eta =\frac{R}{R+r}$.
Таким чином, при збільшенні опору навантаження ККД монотонно зростає, як показано на рис.19-1.
Б. Аби знайти максимальну потужність Pm і відповідне значення ηm, дослідимо на максимум залежність P = f(R), яка визначається виразом (1). Для цього за правилами диференціювання частки знайдемо та прирівняємо до нуля похідну функції f(R):
\(f^{\prime}(R)=\mathcal{\E}^{2}\frac{(R+r)^{2}-2R(R+r)}{(R+r)^{4}}=\frac{\mathcal{\E}^{2}}{(R+r)^3}(r-R)\) = 0.
Отже, f′(R) = 0 при (r – R) = 0), тобто, джерело віддає максимальну корисну потужність, коли опір навантаження збігається із внутрішнім опором джерела:
|
Rm = r. |
(2) |
Відтак підставивши знайдене значення Rm у формулу (1), дістанемо й величину максимальної потужності, яку можна отримати від заданого джерела струму:
|
|
${{P}_{m}}=\frac{{{\E}^{2}}}{4r}$. |
(3) |
При цьому відповідно до співвідношення (2) ККД джерела дорівнює
\(\eta_{m}=\frac{1}{2}\) .
Із отриманих результатів випливають наступні загальні висновки:
1. Неможливо одночасно мати велику потужність і великий ККД. Тому на практиці завжди доводиться робити вибір між потужністю та ефективністю використання енергії: якщо хочемо від транзистора гучної музики, то маємо подбати про запасні батарейки, інакше доведеться обмежитися тихим звучанням.
2. При R < r і корисна і потужність є невелика, і ККД низький, тож енергія джерела фактично витрачається марно. Тому такий режим роботи кіл в електричних пристроях не застосовується.
3. Максимальна потужність, яку можна отримати від джерела живлення, не залежить від споживача й визначається тільки параметрами джерела.
Задача 2.20
У резисторі опором R = 9 Ом, який підключено до джерела з ЕРС ${{\E}_{1}}$ = 10 В, виділяється \(\eta=\) 90 % повної потужності джерела.
Визначити
максимально корисну потужність Pm, яку можна отримати від цього джерела.
|
Дано: ${\E}$ = 10 В
R = 9 Ом
\(\eta=\) 90 %
|
|
Pm - ?
|
Розв’язання
Якщо скористатися виразом (3) із задачі 2.19, то для отримання відповіді не вистачає лише внутрішнього опору джерела r, який легко знайти з формули (2.28):
\(\eta=\frac{R}{R+r}\) \(\Rightarrow\) \(r=\frac{(1-\eta)R}{\eta}\).
Підставивши цей результат у зазначений вираз (3) із попередньої задачі, отримаємо відповідь:
${{P}_{m}}=\frac{{{\E}^{2}}\eta }{4\left( 1-\eta \right)R}$ = 25 Вт.
Задача 2.21
При почерговому підключенні резисторів R1 = 20 Ом і R2 = 45 Ом до акумуляторної батареї через деякий баластний опір R0 на кожному з резисторів виділяється потужність P = 20 Вт. Нехтуючи внутрішнім опором,
визначити
ЕРС батареї $\E$ та струм через неї ${{I}_{0}}$ при замиканні безпосередньо на баластний опір.
|
Дано: R1 = 4 Ом R2 = 9 Ом P = 36 Вт |
|
$\E$-? ${{I}_{0}}$-? |
Розв’язання
Баластний опір обмежує максимальну можливу силу струму через джерело і формально виконує роль його внутрішнього опору. Тож при замиканні джерела безпосередньо на баластний опір якоїсь величини R0 струм у колі за формулою (2.13а) складає
| ${{I}_{0}}=\frac{\E}{{{R}_{0}}}$. |
(1) |
У цьому виразі жодну з величин в умові не задано. Але ситуація полегшується тим, що в обох випадках у колі виділяється однакова потужність, яка визначається виразом (2.26) при r = R0:
|
$P=\frac{{{E}^{2}}R}{{{\left( R+{{R}_{0}} \right)}^{2}}}$. |
(2) |
|
Тож, спочатку прирівнявши вирази (2) при R = R1 і R = R2, після елементарних перетворень знайдемо величину R0:
${{R}_{0}}=\sqrt{{{R}_{1}}{{R}_{2}}}$.
Відтак із того ж таки виразу (2), знайдемо ЕРС джерела:
|
$\E=\sqrt{P}\cdot \left( \sqrt{{{R}_{1}}}+\sqrt{{{R}_{2}}} \right)$ |
|
та за формулою (1) – струм І0 через джерело при замиканні його на баластний опір:
|
${{I}_{0}}=\sqrt{P}\cdot \left( \frac{1}{\sqrt{{{R}_{1}}}}+\frac{1}{\sqrt{{{R}_{2}}}} \right)$. |
|
Обчислення дають:
$\E$ =30 В; ${{I}_{0}}$ = 5А.
Задача 2.22
Споживач, який знаходиться на відстані l = 7,5 км від генератора, отримує потужність P = 100 кВт по двопровідній лінії передач.
Визначити
масу m мідного дроту, яким змонтовано лінію, якщо напруга на вході дорівнює U0 = 6 кВ і втрати потужності в лінії складають k = 3 %.
|
Дано: l = 7,5 км = 7,5·103 м
P = 100 кВт = 105 Вт
U0 = 6 кВ = 6·103 В
k = 3 % = 0,03
|
|
m - ?
|
Розв’язання
Шукана маса проводів дорівнює
|
|
m = 2DlS, |
|
де D – густина міді, S – площа поперечного перерізу дроту. Відтак, виразивши S через опір лінії передач R за формулою (2.8), отримаємо:
|
|
$m=\frac{4D\rho {{l}^{2}}}{R}$. |
(1) |
Таким чином, для отримання відповіді не вистачає лише опору лінії, який за формулою (2.24б) дорівнює
|
$R=\frac{{{P}_{в}}}{{{I}^{2}}}$, |
(2) |
де струм I та втрачена в лінії потужність Pв є неявно задані умовою задачі. Справді,
$I=\frac{{{P}_{0}}}{{{U}_{0}}}$,
де P0 = (P + Pв) – повна потужність, яка надходить у лінію, а Pв= kP за умовою, тож P0 = (1 + k)P. Отже,
$I=\frac{\left( 1+k \right)P}{{{U}_{0}}}$.
Відтак, урахувавши отримані значення Pв та I, за виразом (2) визначимо опір лінії
|
$R=\frac{kU_{0}^{2}}{\left( 1+k \right)P}$ |
(3) |
і, підставивши його у вираз (1), отримаємо загальну відповідь задачі:
|
\(m=\frac{4D\rho{l}^{2}P(1+k)^{2}}{kU_{0}^{2}}\). |
(4) |
Відтак, узявши з таблиць значення потрібних параметрів міді D = 8,9·103 кг/м3 і \(\rho=1,7\cdot{10}^{-8}\) Ом·м, знайдемо числову відповідь:
m ≈ 3,4 т.
В отриманій відповіді (4) варто звернути увагу на те, що при заданих потужності й коефіцієнті втрат необхідна кількість матеріалу дротів є обернено пропорційна квадратові робочої напруги. Це пояснює, чому енергія від електростанцій до споживачів транспортується саме високовольтними лініями електропередач.
Задача 2.23
Трамвай масою m = 50 т спускається зі швидкістю v = 36 км/год по колії з ухилом \(\alpha=0,01\) і  коефіцієнтом опору \(\mu=0,03\).
коефіцієнтом опору \(\mu=0,03\).
Визначити
струм I в обмотці двигуна трамваю, якщо напруга в контактній мережі U = 500 В і ККД двигуна \(\eta=0,8\).
|
Дано: m = 50 т = 5·104 кг
α = 0,01
v = 36 км/год = 10 м/с
μ = 0,03
U = 500 В
η = 0,8
|
|
I - ?
|
Розв’язання
На початках нагадаємо, що ухилом називається зміна висоти полотна дороги над горизонтом, яка припадає на одиницю шляху, тобто – тангенс кута нахилу до горизонту. Коефіцієнтом опору називається відношення сумарної сили опору рухові тіла по якійсь поверхні до його ваги, котра чисельно дорівнює силі нормальної реакції опори N. Відмітимо також, що для пологої дороги ухил практично збігається із кутом нахилу до горизонту в радіанах, а вага тіла – з величиною сили тяжіння.
При рівномірному русі сили тяжіння \(m\vec{g}\), нормальної реакції \(\vec{N}\), опору ${{\vec{F}}_{0}}$ та тяги двигуна \(\vec{F}\), що діють на трамвай (рис. 23), є зрівноважені:
|
$\vec{F}+m\vec{g}+{{\vec{F}}_{0}}+\vec{N}$ = 0. |
|
При цьому через мализну нахилу \(\sin\alpha=\alpha\), і Fо = μmg. Тож у проекціях на горизонтальну вісь маємо:
|
|
\(F+mg\alpha-\mu{mg}=0\) \(\Rightarrow\) \(F=mg(\mu-\alpha)\). |
|
Потужність сили тяги є "корисною потужністю" Рк і, згідно з механікою ([І], формула(4.16)) дорівнює добутку сили тяги на швидкість трамваю:
${{P}_{к}}=\left( \mu -\alpha \right)mgv$.
З іншого боку величина Рк задовольняє співвідношення ([І], формула(4.17)):
${{P}_{к}}=\eta IU$,
де IU = Pз – загальна ("затрачена") потужність двигуна. Отже, шуканий струм
$I=\frac{\left( \mu -\alpha \right)mgv}{\eta u}$ = 245 А.
Задача 2.24
Ніхромовим (питомий опір \(\rho=1\) мкОм·м) дротом діаметром d = 0,4 мм треба намотати нагрівник, який при напрузі U = 220 В і ККД \(\eta=\) 40 % за час \(\tau=10\) хв доводить до кипіння V = 1 л води (питома теплоємність c = 4200 Дж/(кг·К)) із початковою температурою t = 20 °C.
Визначити
необхідну довжину дроту l.
|
Дано: d = 0,4 мм
τ = 10 хв
V = 1 л
t = 20 °C
c = 4200 Дж/(кг·К)
η = 40 %
U = 220 В
ρ = 1 мкОм·м
|
|
l - ?
|
Розв’язання
Шукана довжина дроту l визначається опором нагрівника R (формула (2.8)), при якому в ньому при ввімкненні в мережу за заданий час τ виділяється потрібна кількість теплоти (формула (2.23а))
|
${{Q}_{0}}=\frac{{{U}^{2}}}{R}\tau $. |
(1) |
При цьому безпосередньо на нагрівання води йде частка
$Q=\eta {{Q}_{0}}$,
яка визначається відомою формулою термодинаміки:
|
\(Q=cm(t_{к}-t)\). |
(2) |
Отже, співставивши праві частини виразів (1) і (2), дістанемо:
|
|
$cm\left( {{t}_{к}}-t \right)=\eta \frac{{{U}^{2}}}{R}\tau $. |
|
Далі виразимо опір нагрівника R за формулою (2.8) і переріз дроту за формулою S = (πd2/4) і після нескладних перетворень отримаємо загальну відповідь:
\(l=\frac{\eta{U}^{2}\tau\pi{d^{2}}}{4\rho{c}m(t_{к}-t)}\).
Відтак, врахувавши, що густина води складає 1 г/м3, тож m = 1 кг, після обрахунків знайдемо наступну числову відповідь:
l ≈ 4,35 м.
Задача 2.25
Нагрівник електричного чайника складається з двох секцій. Визначити, за який час t0 у чайнику закипить однакова кількість води з однаковою початковою температурою при а) послідовному і б) паралельному сполученні секцій, якщо при їхньому почерговому ввімкненні цей час складає t1 = 10 хв і t2 = 40 хв, відповідно.
|
Дано: t1 = 10 хв
t2 = 40 хв
|
|
t01 - ? t02 - ?
|
Розв’язання
Позаяк в умові нічого не сказано про втрати тепла, покладемо, що їх немає. В такому разі необхідна для нагрівання води в чайнику кількість теплоти Q визначається формулою (2.23а), і час нагрівання t можна виразити як
|
$t=\alpha R$, |
(1) |
де
$\alpha =\frac{Q}{{{U}^{2}}}$.
Згідно з умовою, коефіцієнт α у виразі (1) у всіх вирпдках має однакову величину. Отже, часи закипання води є пов'язані між собою так само, як і відповідні опори нагрівника. Зокрема, позаяк при послідовному сполученні секцій опір нагрівника R01 = R1 + R2, час закипання води
t01 = t1 + t2 = 50 хв.
Аналогічно при паралельному з'єднанні секцій
${{R}_{02}}=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$,
і час закипання
${{t}_{02}}=\frac{{{t}_{01}}{{t}_{02}}}{{{t}_{01}}+{{t}_{02}}}$ = 8 хв.
Електроліз
Перед розглядом задач із даної теми слід переглянути основні положення молекулярно-кінетичної теорії ([ІІ], п. 1.1).
Задача 2.26. Нікелювання металевої пластинки площею \(S=120\ {см^{2}}\) проводиться протягом t = 5 год при силі струму в електролітичній ванні I = 0,3 А. Валентність нікелю n = 2, атомна маса A = 58,7 ·10–3 кг/моль, густина \(\rho=9\cdot{10^{3}}\) кг/м3. Визначити товщину покриття d.
Задача 2.27. При електролізі води через ванну пропустили заряд q = 30 кКл і одержали V = 2 л кисню при тиску P = 100 кПа. Визначити температуру газу t°С.
Задача 2.26. Нікелювання металевої пластинки площею \(S=120\ {см^{2}}\) проводиться протягом t = 5 год при силі струму в електролітичній ванні I = 0,3 А. Валентність нікелю n = 2, відносна атомна маса A = 58,7 г/моль, густина \(\rho=9\cdot{10^{3}}\) кг/м3.
Визначити
товщину покриття d.
|
Дано: S =120 см2 = 1,2·10-2 м2
t = 5 год = 1,8·104 с
I = 0,3 А
n = 2
A = 58,7·10–3 кг/моль
\(\rho=9\cdot{10^{3}}\) кг/м3
|
|
d - ?
|
Розв’язання
При заданій площі пластини S та густині речовини ρ товщина покриття дорівнює
|
|
$d=\frac{m}{\rho S}$, |
(1) |
де маса шару покриття m визначається об'єднаним законом електролізу (2.32):
|
|
$m=\frac{1}{F}\cdot \frac{A}{n}\cdot It$. |
(2) |
Підставивши це значення у вираз (1), отримаємо відповідь:
$d=\frac{AIt}{Fn\rho S}$
і в числах
d ≈ 18 мкм.
Задача 11.27
При електролізі води через ванну пропустили заряд q = 30 кКл і одержали V = 2 л кисню при тиску P = 100 кПа.
Визначити
температуру газу t°С.
|
Дано: q = 30 кКл = 3·104 Кл
V = 2 л = 2·10-3 м3
P = 100 кПа = 105 Па
F = 9,65·104 Кл/моль
|
|
T - ?
|
Розв’язання
Згідно з рівнянням Клапейрона ([ІІ], п. 1.1), шукана температура становить
|
$T=\frac{MPV}{Rm}$, |
(1) |
де R – універсальна газова стала, M – молярна, а m – "звичайна" маса газу.
Отриманий кисень O2 є одним із продуктів електролізу води, тож у виразі (1) величина m за першим законом Фарадея (1.29) складає
| m = kq, |
(2) |
де електрохімічний еквівалент k можна знайти за другим законом Фарадея, врахувавши специфіку електролізу води. А саме, те, що при дисоціації молекул H2O безпосередньо утворюються не молекули кисню О2, а йони O–, котрі лише потім відновлюються й об'єднуються в молекули на катоді електролітичної ванни (рис. 27). Тож у виразі (2.30) замість молярної маси кисню M має фігурувати його відносна атомна маса A = (M/2), і
$k=\frac{M}{2nF}$.
Отже, за виразом (2) маса отриманого газоподібного кисню дорівнює
|
$m=\frac{Mq}{2nF}$. |
|
Відтак, підставивши це значення у вираз (1) і врахувавши валентність кисню n = 2, дістанемо загальну відповідь
$T=\frac{4FPV}{Rq}$
і, після обрахунків, числове значення температури отриманого кисню:
T≈ 310 K = 37 °С.
3. Задачі для самостійної роботи
|
Рівень А |
|
|
2.28. |
Визначити кількість електронів, що потрапляють на анод вакуумного діода за 1 хв при при силі струму 240 мА. [9·1019] |
|
2.29. |
Визначити швидкість упорядкованого руху електронів у провіднику з перерізом 0,5 мм2 при силі струму 10 А, якщо концентрація вільних електронів у ньому становить 5·1022 см–3 . [2,5 мм/с] |
|
2.30. |
Визначити сумарний заряд носіїв, який припадає на одиницю довжини провідника, якщо швидкість їхнього впорядкованого руху при силі струму 10 А складає 1 мм/с. [10 кКл] |
| 2.31. |
Два з'єднані стрижні з одного металу однакової довжини і з відношенням діаметрів (d1/d2) = 2 підключили до джерела. Визначити співвідношення величин (І1:І2) і густин (j1:j2) струму в стрижнях, якщо їхнє з'єднання є: а) послідовне і б) паралельне. [1:1, 1:4; 4:1, 1:1] |
| 2.32. |
Визначити діаметр мідної (ρ1 = 1, 7·10–8 Ом·м) дротини, якою можна замінити залізний (ρ2 = 1, 36·10–7 Ом·м) провідник такої самої довжини, котрий складається з восьми жил діаметром 0,2 мм кожна. [0,2 мм] |
|
2.33. |
Довгу дротину опором 16 Ом розрізали на 16 однакових частин і з'єднали їх паралельно. Визначити опір багатожильного провідника, що утворився. [62,5 мОм] |
|
2.34. |
До паралельно сполучених резисторів 2 Ом і 3 Ом послідовно приєднали резистор 1,8 Ом. Знайти опір ланцюжка, що утворився. [3 Ом] |
|
2.35. |
Визначити напруженість електричного поля у мідному (ρ = 1,7·10–7 Ом·м) дроті з перерізом о,5 мм2 при силі струму 10 А . [0,34 В/м] |
|
2.36. |
Загальна напруга на послідовно з'єднаних резисторах опором 3 Ом і 5 Ом дорівнює 24 В. Визначити напругу на кожному резисторі. [9 В; 15 В] |
| 2.37. |
Загальна сила струму, що проходить по паралельно з'єднаних резисторах опором 1 Ом і 3 Ом дорівнює 2 А. Визначити струм у кожному резисторі. [15 А; 0,5 А] |
| 2.38. |
Яку максимальну напругу можна виміряти вольтметром із внутрішнім опором 100 Ом і шкалою 10 В, якщо до нього приєднати додатковий опір 1 кОм? [110 В] |
| 2.39. |
Визначити напругу на клемах акумулятора з ЕРС 12 В, що є замкнений на резистор із утричі більшим опором. [9 В] |
| 2.40. |
До резистора із струмом підключено два послідовно з’єднані між собою вольтметри, котрі показують 100 В і 80 В, відповідно. Визначити опір другого вольтметра, якщо опір першого дорівнює 500 Ом. [400 Ом] |
| 2.41. |
Певний об’єм води нагрівають у титані з нагрівником із трьох однакових секцій, що з’єднані послідовно. Яку кількість води можна так само нагріти за той самий час при паралельному сполученні секцій? [Удев’ятеро більшу] |
| 2.42. |
Визначити потужність, яку споживає лампочка з опором спіралі 8 Ом при підключенні до батарейки з ЕРС 4,5 В і внутрішнім опором 1 Ом [4 Вт] |
| 2.43. |
При опорі навантаження 4 Ом напруга на клемах джерела із внутрішнім опором 2 Ом дорівнює 6 В. Визначити потужність та ККД джерела. [13,5 Вт; 67%] |
| 2.44. |
При зарядці акумулятора з ЕРС 1,3 В зарядний струм та напруга на клемах складають 1А і 2В. Визначити потужність, яку споживає акумулятор, і кількість тепла, що виділяється в ньому за 1 хв. [2 Вт; 42 Дж] |
| 2.45. |
Визначити ККД акумулятора з ЕРС 4,5 В, якщо при підключенні навантаження напруга на клемах впала до 4,0 В. [89%] |
| 2.46. | Атомна маса срібла дорівнює 108 г/моль , валентність 1, електрохімічний еквівалент 1,18·10–7 кг/Кл. Визначити електрохімічний еквівалент золота, якщо його атомна маса 197 г/моль і валентність 3. [7,17·10–8 кг/Кл] |
Рівень Б
|
2.47. |
Сила струму в провіднику рівномірно зростає за перші 3 с від нуля до 0,5 А , а за наступні 5 с – ще на стільки ж. Визначити середню силу струму за весь час. [≈ 0,56 А] |
|
2.48. |
Визначити дрейфову швидкість електронів у мідному провіднику перерізом 1 мм2 при силі струму 16 А, вважаючи на що на кожен атом припадає один електрон провідності. [≈1 мм/с] |
|
2.49. |
Широкий пучок електронів, який створює струм густиною 1 мкА/см2, падає на поверхню провідної кулі діаметром 20 см. За який час куля набуде потенціалу 200 В? Дією поля кулі на рух електронів знехтувати. [≈1,8 мкс] |
|
2.50. |
Підключений до джерела струму резистор із температурою 20°С опустили в окріп (100°С). Визначити, на скільки змінилися а) опір резистора та б) величина струму в ньому при температурному коефіцієнті опору 0,005 К–1. [а) ≈36%; б) ≈27% ] |
|
2.51. |
Опір між двома точками дротяного кільця є в 6,25 разів менший за повний опір дроту, з якого виготовлено кільце. Визначити, в якому відношенні вказані точки ділять довжину кільця? [1:4] |
| 2.52. |
 У схемі рис. 52 R = 1,73 Ом. Визначити величину r, якщо опір з'єднання дорівнює R. [1 Ом] |
| 2.53. |
 Ланцюжок, який складається з резистора опором R і реостата з таким самим повним опором, включено в електричне коло точками а і b (рис. 53). Визначити й показати на графіку залежність Rab(r) опору ланцюжка від опору r робочої частини реостата. |
| 2.54. |
 Три резистори з’єднали "трикутником" (рис 54). Визначити величини опорів R1, R2, R3, якщо R1 = 2R2, й опори трикутника Rab = 20 Ом і Raс = 15 Ом. [R1 = 40 Ом, R2 = R3 = 20 Ом] |
| 2.55. |
До джерела струму підключено реостат із початковим опором рівним внутрішньому опорові джерела. Як і в скільки разів зміниться напруга на реостаті при збільшенні його опору вдвічі? [збільшиться в 1,5 раза] |
| 2.56. |
Визначити похибку ε (%), яку вносить у покази амперметра підключення шунта, що розширює діапазон вимірювань у n = 10 разів. Вказівка. Скористатися результатом задачі 2.13. [ε = (1/n) =10%] |
| 2.57. |
 Два однакові амперметри та два однакові вольтметри, що увімкнені, як на рис. 57, показують І1 = 100 мкА , І2 = 99 мкА, U1 = 10 В . Визначити покази другого вольтметра U2. [100 мВ] |
| 2.58. |
При замиканні акумулятора на резистор 5 Ом струм у колі дорівнює 3 А, а при замиканні на резистор 2 Ом – 5 А . Визначити силу струму короткого замикання акумулятора. [9 А] |
| 2.59. |
Акумулятор з ЕРС 25 В і внутрішнім опором 1 Ом заряджають від мережі з напругою 40 В через резистор 5 Ом. Визначити напругу на клемах акумулятора при зарядці [27,5 В] |
| 2.60. |
 Визначити початкову силу струму в резисторі та кінцеву напругу на конденсаторі після замикання ключа К у схемі рис 60 при R1 = R2 = 100 Ом і \(\E\) = 50 В. [0,5 А; 25 В] |
| 2.61. |
Нагрівник електричної плитки складається з трьох однакових секцій опором по 60 Ом, які можна вмикати як поодинці, так і в будь-яких комбінаціях. Знайти всі величини (Вт) теплової потужності, які можна отримати при ввімкненні нагрівника в мережу з напругою 120 В. [80, 120, 160, 240, 360, 480, 720]
|
| 2.62. |
Певний об’єм води нагрівають у титані з нагрівником із трьох однакових секцій, що з’єднані послідовно. Яку скільки води можна так само нагріти за той самий час при паралельному сполученні секцій? [Удев’ятеро більшу] |
| 2.63. |
У випарнику з робочим опором нагрівника 10,5 Ом за 1 хвилину випаровується 103 мл води. Знайти силу струму, котрий споживає випарник. Питома теплота пароутворення води 2,3 МДж/кг. [20 А] |
| 2.64. |
На плоский конденсатор ємності 0,1 мкФ із недосконалим діелектриком проникністю ε = 6 і питомим опором ρ = 1,6 109 Ом·м подано напругу 100 В. Визначити кількість теплоти, що виділяється в конденсаторі за 1 секунду. [11,8 мВт] |
| 2.65. |
Раніше для захисту електричних пристроїв від короткого замикання та ненормативних стрибків напруги в мережі використовували топкі запобіжники – короткі тонкі дротинки, що швидко розплавлюються при різкому збільшенні струму. Оцінити час "спрацювання" такого запобіжника при стрибку струму до 100 А, якщо він виготовлений з мідного дроту діаметром 0,2 мм. [≈ 30 мс] |
| 2.66. |
При струмі 2 А в навантаженні акумулятора виділяється потужність 22 Вт, а при 6 А – 54 Вт. Знайти струм короткого замикання акумулятора. [24 A] |
| 2.67. |
Моторчик іграшкового електровоза потужністю 4 Вт живиться від батарейки з ЕРС 4,5 В і внутрішнім опором 0,5 Ом. Визначити ККД батарейки. [80 %] |
| 2.68. |
Струм короткого замикання джерела з ЕРС \(\E\) дорівнює І0. Визначити максимальну потужність Рm, яку можна отримати в навантаженні. [Рm = \(\E{I_0}/4\)] |
| 2.69. |
Відомо, що одну й ту саму корисну потужність від заданого джерела живлення можна отримати при двох різних значеннях опору навантаження. Встановити зв'язок між ККД джерела η1 і η2 за вказаної умови. [η1 + η2 = 1] |
| 2.70. |
При електролізі розчину сірчаної кислоти H2SO4 при потужності струму у ванні 50 Вт за 50 хв отримали 0,3 г водню. Визначити опір електроліту. [0,1 Ом] |
Рівень В
|
2.71. |
Струм в електронно-променевій трубці при напрузі 2 кВ дорівнює 400 мкА. Визначити силу тиску на екран, яка створюється електронним пучком за умови, що всі електрони поглинаються. [60 нН] |
|
2.72. |
 Із дроту, опір одиниці довжини якого складає R1, виготовлено круглий каркас радіусом 0,5 м із двома взаємно перпендикулярними діаметральними перемичками (рис. 72). Визначити опір R каркасу між точками a i b. [R = 0,44 R1]
|
|
2.73. |
Для тестування пошкодженого двожильного електричного кабелю довжиною 2,5 км на вхід подають напругу 10 В і вимірюють силу струму при 1) розімкненому та 2) замкненому виході. Визначити опір ізоляції в місці пошкодження та відстань до нього, якщо в першому випадку отримали 2 А, а в другому – 2,5 А. Опір одиниці довжини дроту, з якого виготовлено кабель, складає 1 (Ом/км). [2 Ом; 1,5 км]
|
| 2.74. |
Нехтуючи опором дротів і джерела, визначити силу струму в перетинці ab у схемі рис. 74. [\(\E/7r\)] |
| 2.75. |
 Визначити різницю потенціалів між точками a i b в схемі рис 75. [18${\E}$/11] |
| 2.76. |
Робочий струм в обмотці електродвигуна дорівнює 5 А при напрузі 12 В. Визначити потужність двигуна, якщо в момент увімкнення сила струму в його обмотці складає 24 А. [47,5 Вт] |
| 2.77. | Конденсатор з ємністю С і напругою U додатково заряджають від джерела з ЕРС 5U через резистор з великим опором R. Визначити кількість тепла, що виділиться при цьому. [8CU2] |
Розділ ІІІ. Магнітне поле та електромагнітна індукція
Магнітне поле – це складова електромагнітного поля, обумовлена рухом зарядів, тож створюється вільними рухомими зарядженими частинками та провідниками із струмом. Відповідно, магнітне поле діє теж лише на рухомі заряди та провідники із струмом.
На практиці як джерела магнітного поля використовуються також постійні магніти – тіла, в атомах яких рух електронів є узгодженим.
Магнітне поле є органічно пов'язане з іншою складовою електромагнітного поля – електричним полем, одним із проявів чого є електромагнітна індукція.
Далі розглянуто:
1. Теоретичні відомості
Далі стисло розглянуто наступні питання:
1.1. Вектор індукції магнітного поля
1.2. Дія магнітного поля на рухомі заряди
1.3. Провідники зі струмом у магнітному полі
1.1. Вектор індукції магнітного поля
Дослідні факти стосовно дії магнітного поля на рухомі заряди свідчить про наступне.
1. Серед безлічі можливих напрямів руху заряду в магнітному полі в кожній точці є один такий, при русі вздовж якого магнітна сила на заряд не діє. Цей "особливий" напрям прийнято за напрям магнітного поля в даній точці.
2. Величина (модуль) магнітної сили ${{{F}}_{m}}$, що діє на рухомий заряд є прямо пропорційна до величини заряду q та перпендикулярної до напрямку поля складової його швидкості ${{v}_{\bot }}$:
|
${{{F}}_{m}}$ = q${{v}_{\bot }}$B. |
(3.1) |
Це означає, що віношення сили до заряду
|
$B=\frac{{{F}}}{q{{v}_{\bot }}}$ |
(3.1а) |
залежить тільки від поля. Отож величина \({B}\), котра називається індукцією магнітного поля або магнітною індукцією, є його силовою характеристикою. Вона вимірюється в теслах (означення одиниці 1Тл див. у п.1.5).
Магнітна індукція є вектором, як і напруженість електричного поля \(\vec{E}\), але на відміну, зв'язок між векторами \(\vec{B}\) і ${{\vec{F}}_{m}}$ є більш складним і визначається так званим правилом правого гвинта (або свердлика):
якщо правий гвинт найкоротшим шляхом обертати від вектора магнітної сили ${{\vec{F}}_{m}}$, що діє рухомий заряд q > до вектора швидкості $\vec{v}$, то вектор \(\vec{B}\) буде спрямований в напрямку вкручування гвинта.
Також магнітне поле, як і електричне, зображують лініями магнітної індукції, дотичні до котрих у кожній точці збігаються із напрямом вектора \(\vec{B}\). Але знову на відміну від електричного поля, лінії магнітної індукції безпосередньо не визначають напрямом магнітної сили, тож не є силовими лініями в буквальному сенсі. Крім того, позаяк магнітне поле породжується не зарядами як такими, а їхнім рухом (зокрема електричним струмом), лінії магнітної індукції є замкнутими, а їхній напрям для поля провідника зі струмом визначається теж правилом правого гвинта:
якщо правий гвинт укручувати в напрямку струму, то напрям обертання гвинта в кожній точці збігатиметься з напрямом вектора магнітної індукції в цій точці,
як показано на рис. 3.1б для поля прямого провідника із струмом.
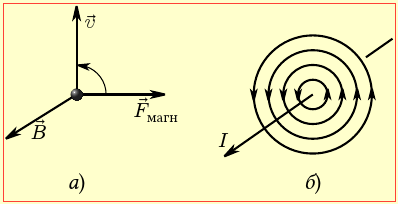
В обмеженій області простору можна створити однорідне магнітне поле \(\vec{B}\) = const, лінії котрого являють собою рівновіддалені паралельні відрізки. Таким є поле всередині довгої циліндричної котушки із струмом (соленоїда), що спрямоване вздовж його осі за правилом правого гвинта. Однорідним є також поле у вузькому зазорі між полюсами кільцевого магніту (рис. 3.2).

Зазначимо також, що як і електричне, магнітне поле підпорядковується принципу суперпозиції:
індукція магнітного поля \(\vec{B}\), що створюється кількома струмами, в будь-якій точці дорівнює сумі індукцій полів \[\vec{B}\)і, створюваних у цій точці кожним зі струмів окремо:
|
$\vec{B}={{\vec{B}}_{1}}+{{\vec{B}}_{2}}+\ldots {{\vec{B}}_{i}}+\ldots =\sum{{{{\vec{B}}}_{i}}}$ |
(3.2) |
Це стосується й будь-яких інших магнітних полів, позаяк принцип суперпозиції відображає той факт, що незалежно від походження, магнітні поля не впливають одне на одного.
|
|
|
1.2. Дія магнітного поля на рухомі заряди
Сила Лоренца. Таку назву має магнітна сила, що діє на рухомі заряди. (Примітка. У випадку електромагнітного поля сила Лоренца включає й електричну компоненту).
Модуль сили Лоренца, відповідно до формули (3.1), визначається перпендикулярною до поля складовою швидкості заряду \({v}_{\bot}\)= v·sinα (рис. 3.3):
|
$F=qvB\sin \alpha $. |
(3.3) |
Напрям цієї сили задовольняє наступне правило правого гвинта:
якщо правий гвинт найкоротшим шляхом обертати від напрямку швидкості зарядженої частинки до напрямку індукції магнітного поля, то гвинт буде вкручуватись у напрямку сили Лоренца, що діє на позитивний заряд.
Якщо заряд рухається перпендикулярно до напрямку поля, то
|
$F=qvB $. |
(3.3а) |
Рух зарядів в однорідному магнітному полі. Позаяк сила Лоренца завжди спрямована перпендикулярною до напряму переміщення заряду, вона не виконує роботи, тож і не змінює кінетичну енергію та величину швидкості частинки. Таким чином,
|
рух заряджених частинок під дією сили Лоренца завжди є рівномірним і криволінійним, а прискорення – доцентровим. |
При цьому форма траєкторії визначається конфігурацією магнітного поля та напрямком початкової швидкості частинки й у загальному випадку є складною. Виняток становить лише рух заряду в однорідному полі $\vec{B}$ = const, коли за наявності сили Лоренца, є можливі тільки два випадки.
1. Швидкість спрямована перпендикулярно до напрямку поля. В такому разі, як випливає із законів механіки (див. [І], ...),
частинка із зарядом q, масою m і швидкістю v рухається в перпендикулярній до поля площині по колу (рис. 3.5 ) радіуса
| \(R=\frac{mv}{qB}\) = $\frac{v}{{{q}_{п}}B}$, |
(3.4) |
де величина
${{q}_{п}}=\frac{q}{m}$ (Кл/кг)
називається питомим зарядом частинки.

(Примітка. Напрям руху відносно напрямку поля залежить від знаку заряду й на рис. 3.4 показаний для q > 0).
Період обертання T = (2πR/v) і колова частота (кутова швидкість) ω = (2π/T) заряду визначаються формулами:
$T=\frac{2\pi m}{qB}$ = $\frac{2\pi }{{{q}_{п}}B}$; |
(3.5) |
|
$\omega =\frac{qB}{m}$ = ${{q}_{п}}B$. |
(3.5а) |
Як видно, вони не залежать від швидкості, тобто
в однорідному магнітному полі частинки з однаковим питомим зарядом рухаються синхронно.
Тож, якщо уявити, що в деякій точці однорідного поля перпендикулярно до його напряму впорснули пучок однакових частинок, які мають різні швидкості, то, рухаючись далі по різних траєкторіях, вони з інтервалом часу Т будуть знов і знов сходитись у початковій точці.
2. Рух зарядженої під кутом до напрямку поля. У цьому випадку швидкість частинки \(\vec{v}\) можна розкласти на перпендикулярну \(\vec{v}_{\bot}\) і паралельну \(\vec{v}_{\parallel}\) складові (рис. 3.5а) :

\(\vec{v}=\vec{v}_{\bot}+\vec{v}_{\parallel}\)
і вважати, що вона одночасно обертається по колу радіусом (3.4) зі швидкістю \({v}_{\bot}\)= v·sinα і періодом (3.5) у перпендикулярній до поля площині й поступально рухається вздовж напряму поля зі швидкістю \(v_{\|}=v\cos\alpha\). Тож її траєкторією є гвинтова лінія (рис. 3.5б) з радіусом витка R і кроком (відстанню між витками h = \(v_{\|}\)T), котрі за формулами (3.4) і (3.5) дорівнюють:
|
\(R=\frac{mv\sin\alpha}{qB}\) = $\frac{v\sin \alpha }{{{q}_{п}}B}$; |
(3.6) |
|
\(h=\frac{2\pi{mv}\cos\alpha}{qB}\) = $\frac{2\pi v\cos \alpha }{{{q}_{п}}B}$. |
(3.7) |
На завершення слід зауважити, що отримані формули не враховують силу тяжіння. Тому вони за замовчуванням стосуються лише субмікроскопічних заряджених частинок, як от електрон, протон, іон, тощо.
1.3. Провідники зі струмом у магнітному полі
Сила Ампера. Магнітне поле діє не лише на окремі рухомі заряди, а й на провідники зі струмом, хоча вони як ціле є незаряджені. Це легко зрозуміти. Сила Лоренца, що діє в провіднику на рухомі електрони-носії струму, надає їм поперечного імпульсу, котрий через зіткнення передається іонам ґратки, створюючи силу, що діє на провідник як ціле. Ця сила називається силою Ампера і, ясна річ, за напрямом і модулем дорівнює сумарній силі Лоренца, що діє на носії струму в провіднику і теж є поперечною. Відповідно
напрям сили Ампера визначається правилом правого гвинта:
якщо правий гвинт найкоротшим шляхом повертати від напряму струму до напряму магнітного поля, то він буде вкручуватись у напрямку сили Ампера, що діє на провідник, рис.3.6а .
На практиці часто використовують рівнозначне мнемонічне правило лівої руки (рис. 3.6б):
якщо долоню лівої руки розташувати так, аби лінії магнітного поля входили в неї, а чотири пальці були спрямовані у бік протікання струму в провіднику, то відставлений великий палець укаже напрям сили Ампера.
Величину сили Ампера, що діє на прямий провідник довжини l зі струмом I в однорідному магнітному полі з індукцією \(\vec{B}\) = const, можна визначити з формули сили Лоренца (3.3). Для цього в ній v слід розглядати як швидкість упорядкованого руху носіїв струму, а q – як їхній повний заряд:
$q=e\cdot n\cdot Sl$,
де e , n – заряд і концентрація носіїв, а S і l – площа поперечного перерізу та довжина провідника. Тоді модуль сили Ампера
$F=env\cdot S\cdot lB\sin \alpha $.
Відтак, урахувавши вирази (2.3) і (2.4), отримаємо
|
\(F = IlB\sin\alpha\), |
(3.8) |
де \(\alpha\) – кут між напрямками магнітного поля та струму в провіднику (рис.12.5).
(Примітка. Якщо поле не є однорідним, а провідник прямим, то за отриманою формулою визначають сили, що діють на окремі малі ділянки провідника, і по тому – їхню рівнодійну).
Якщо провідник розташовано перпендикулярно до напрямку поля, то сила Ампера є максимальна й дорівнює
|
\(F=IlB\). |
(3.8а) |
Тому, переписавши цей вираз у вигляді
$B=\frac{F}{Il}$,
можна дати наступне альтернативне означення магнітної індукції:
індукцією магнітного поля B називається величини, що чисельно дорівнює максимальній силі, котра діє в однорідному магнітному полі на прямий провідник одиничної довжини із струмом одиничної величини.
Контур із струмом у магнітному полі. Уявлення про "провідник із струмом у магнітному полі" є абстракцією, бо реально постійний струм може протікати тільки по замкненому контуру. При цьому сили Ампера, що діють на протилежні ділянки вміщеного в поле контуру, мають протилежний напрям і створюють відповідний момент сил або обертовий момент (див. [І], розділ V, п. 5.1), який намагається повернути контур так, аби напрям струму в ньому був пов'язаний з напрямком зовнішнього поля правилом правого гвинта. Цей момент, на загал, складно залежить від розмірів і форми контуру та характеристик поля, але момент сил, що діють на плоский контур із струмом в однорідному магнітному полі, визначається простою формулою:
|
\(M=ISB\sin\alpha\), |
(3.9) |
де I, S – сила струму і площа контуру, B – індукція магнітного поля, \(\alpha\) – кут між напрямом поля та нормаллю (перпендикуляром) до площини контуру (рис.3.7 ). При цьому поле завжди намагається повернути контур так, аби напрям позитивної нормалі до нього \(\vec{n}\) збігався із напрямом поля\(\vec{B}\).

Принагідно зауважимо, що за конфігурацією магнітного поля штабові магніти, зокрема стрілки магнітних компасів, є схожі на контури із струмом. Через це стрілка компаса в кожному місці орієнтується в напрямку магнітного поля Землі (по магнітному меридіану), вказуючи напрями на магнітні полюси, що розташовані поблизу від географічних.
1.4. Електромагнітна індукція
Електромагнітна індукція. Електричне та магнітне поля є "двома сторонами однієї медалі" – електромагнітного поля. Тож так само, як електричний струм створює магнітне поле, магнітне поле за певних умов породжує ("індукує") електричний струм. Цей феномен називається електромагнітною індукцією і кількісно описується через магнітний потік – величину, що характеризує поле не в точці, а на заданій поверхні й має наступне означення:
магнітним потоком Ф однорідного поля з індукцією B крізь плоску поверхню площею S (рис.3.8 12.3) називається величина
| Ф = BScosα, |
(3.10) |
де α – кут між напрямками магнітної індукції ${\vec{B}}$ і позитивної нормалі (перпендикуляра) ${\vec{n}}$ до цієї поверхні.
(Примітка. Позитивною нормаллю називається одиничний вектор ${\vec{n}}$, напрям якого узгоджено з напрямом струму в контурі правилом правого гвинта).
У випадку неоднорідного поля чи не плоскої поверхні величина Ф визначається як сума потоків через всі елементарні ділянки поверхні.
Одиниця магнітного потоку називається вебер (Вб) (означення див. п. 1.5).

| Ф0 = BS. |
(3.10а) |
Дослід свідчить, що
при будь-якій зміні магнітного потоку крізь поверхню, обмежену замкненим контуром, у ньому виникає ("індукується") електрорушійна сила (ЕРС).
У цьому полягає явище електромагнітної індукції (ЕМІ). Величину ЕРС індукції визначає основний закон ЕМІ (закон Фарадея):
електрорушійна сила індукції в контурі дорівнює взятій з протилежним знаком швидкості зміни магнітного потоку крізь поверхню обмежену цим контуром:
Вираз (3.11) є універсальним: він визначає ЕРС, яка індукується в кожен момент часу в усякому контурі незалежно від причини зміни потоку та вигляду залежності Ф(t). Зокрема, при рівномірній зміні потоку індукується постійна ЕРС
де \(\Delta\Phi\) – зміна потоку за будь-який заданий проміжку часу \(\Delta{t}\). При нерівномірній зміні потоку цей вираз визначає середню ЕРС індукції $\bar{E}$ за заданий проміжок часу. Напрямок індукційного струму визначає правило Ленца: індукційний струм у контурі завжди має такий напрям, при якому він власним магнітним полем перешкоджає зміні магнітного потоку, що спричинює цей струм. Аби формально відобразити це у виразі основного закону ЕМІ, силу струму розглядають як алгебраїчну величину, що задовольняє наступне "правило знаків": індукційний струм є додатнім, якщо циркулює за правим гвинтом відносно напряму магнітного поля, що його генерує. За такої умови знак індукційного струму в кожному випадку збігається зі знаком ЕРС, який виходить за виразами (3.11) і (3.11а). Як це "працює", ілюструє рис. 3.9 12.9 для двох конкретних випадків. а) Контур рухається в постійному неоднорідному магнітному полі \(\vec{B}\) у бік його послаблення. У такому разі \(\Delta\Phi<0\), і за виразом (3.11) \(\E>0\). Тож і індукційний струм \(I_i>{0}\), тобто тече, як показано на рис. 3.9а, і своїм полем \(\vec{B}^{\prime}\) підживлює поле \(\vec{B}\) у повній відповідності до правила Ленца. б) Нерухомий контур знаходиться у магнітному полі, що підсилюється з часом, рис. 3.9б. У такому разі \(\Delta\Phi>0\), тож \(\E<0\) і \(I_i<0\). Отже, тепер порівняно з попереднім випадком індукційний струм має зворотній напрям, і знов у відповідності із правилом Ленца, перешкоджає зміні поля \(\vec{B}\). На практиці часто використовують контури у вигляді дротяних котушок, у витках яких ЕРС індукції ${{\E}_{i}}$ є узгодженими. Тож повна ЕРС в котушці $\E=\sum{{{\E}_{i}}}$ і визначається швидкістю зміни сумарного магнітного потоку крізь її витки. Зокрема в соленоїді (циліндричній котушці з N однакових витків) повний потік
де \(\Phi_{1}\) – потік крізь один виток (інакше, через поперечний переріз котушки). Відповідно, за виразами (3.11) і (3.11а) ЕРС індукції в соленоїді дорівнює
в загальному випадку та
при рівномірній зміні потоку. |
|
Самоіндукція. Лінії індукції магнітного поля всякого контуру зі струмом І, приміром, як на рис. 3.10, перетинають будь-яку обмежену ним поверхню. Через це створюється прямо пропорційний до сили струму власний магнітний потік, або потік самоіндукції контуру \(\Phi_{с}\)
Величина L називається коефіцієнтом самоіндукції, або індуктивністю контуру й вимірюється в генрі (Гн), означення див. у п. 1.5.
|
Індуктивність на загал залежить від магнітних властивостей середовища та геометрії контуру, зокрема, для соленоїда (циліндричної котушки) – його довжиною та діаметром і кількістю витків.
При зміні власного потоку в контурі спостерігається самоіндукція, тобто виникає електрорушійна сила (ЕРС самоіндукції), що за основним законом ЕМІ (3.11) дорівнює:
|
${{\E}_{c}}=-{{\left( LI\left( t \right) \right)}^{\prime }}=-\frac{d\left( LI \right)}{dt}$. |
(3.15) |
У загальному випадку цей вираз є складним, позаяк при наявності в котушці магнітного осердя чи деформації дротяного контуру індуктивність може неконтрольовано змінюватися з часом. Але, коли індуктивність не змінюється (L = const) вираз (3.15) спрощується і набуває вигляду:
|
${{\E}_{c}}=-L{{\left( I\left( t \right) \right)}^{\prime }}=-L\frac{dI}{dt}$. |
(3.15а) |
При рівномірній зміні струму величина ${{\E}_{c}}$ визначається простою формулою
|
${{\E}_{c}}=-L\frac{\Delta I}{\Delta t}$. |
(3.15б) |
У загальному випадку формула (3.15б) визначає середню ЕРС самоіндукції за час Δt.
Енергія магнітного поля. Якщо електричне коло не має помітної індуктивності, струм у ньому встановлюється відразу після включення джерела живлення. Але в контурі з великою індуктивністю в момент підключення джерела виникає зустрічна ЕРС самоіндукції, що гальмує встановлення струму. На її подолання джерело в процесі встановлення струму витрачає додаткову енергію, що йде не на нагрівання провідників, а на створення магнітного поля. Тож, позаяк енергія як така не може безслідно зникати, маємо констатувати, що магнітне поле має енергію. В теорії доводиться, що енергія магнітного поля контуру з індуктивністю L і струмом I дорівнює
|
1.5. Одиниці магнітних величин
|
У системі SI одиниці магнітної індукції (тесла) та індуктивності (генрі) встановлюються через одиницю магнітного потоку на основі співвідношень (3.10а) і (3.14), а ''вихідна'' одиниця магнітного потоку вебер означається на основі закону електромагнітної індукції (3.11а)) наступним чином. Вебер (1Вб) – це такий магнітний потік, який при рівномірному зменшенні за час 1с до нуля створює в зчепленому з ним контурі ЕРС індукції 1В, отже 1 Вб = 1 В·с. Тесла (1Тл) – індукція однорідного магнітного поля, що крізь розташовану перпендикулярно до нього плоску поверхню 1м2 створює потік 1Вб: \(1\ {Тл}=1\ \frac{Вб}{м^{2}}\). Генрі (1Гн) – індуктивність контуру, власний магнітний потік якого дорівнює 1Вб при силі струму 1А: \(1\ {Гн}=1\ \frac{Вб}{А}\). |
2. Приклади розв'язування задач
Представлені нижче приклади розв'язування задач поділен0 на наступні тематичні групи.
Рух заряджених частинок у магнітному полі
Індукція магнітного поля
|
У задачах зазвичай фігурують магнітне поле прямого струму, що є скрізь перпендикулярне до нього, та поле на осі кільцевого контуру зі струмом, яке спрямовано вздовж неї. Задача 3.1. Спостерігач на нерухомому візку вимірює індукцію магнітного поля довгого провідника зі струмом й отримує значення \(\vec{B}\). Визначити, яким стане результат вимірювання \(\vec{B}\)′, коли візок почне рухатись уздовж провідника зі швидкістю впорядкованого руху (дрейфу) електронів-носіїв струму. Задача 3.2. Довгий прямий дріт зі струмом зігнуто під прямим кутом. Визначити напрям магнітного поля на лінії однієї з половин провідника. Задача 3.3. Магнітне поле створюється двома довгими розташованими на деякій відстані один від одного прямими провідниками зі струмом. Визначити вектор індукції \(\vec{B}_{0}\) поля у віддалених від кожного з них на таку саму відстань точках, якщо в них індукція поля одного провідника B = 0,1 мТл. Розглянути випадки, коли напрями струмів: а) однакові і б) протилежні. Задача 3.4. На двох довгих прямих ізольованих провідниках із однаковим струмом у різний спосіб роблять "петлі"однакового розміру і форми, як показано у розв'язку. При цьому індукція магнітного поля в центрі петлі, відповідно, складає Bа = 400 мкТл і Bб = 200 мкТл. Визначити індукцію магнітного поля, що створюється в цій точці прямою (${{B}_{-}}$) і викривленою (${{B}_{о}}$) частиною провідника окремо. |
Задача 3.1. Спостерігач на нерухомому візку вимірює індукцію магнітного поля довгого провідника зі струмом й отримує значення \(\vec{B}\).
Визначити,
яким стане результат вимірювання \(\vec{B}\)′, коли візок почне рухатись у тому самому напрямі й з тією самою швидкістю, що й вільні електрони в провідникові.
|
Дано: \(\vec{B}\) |
|
\(\vec{B}\)′ |
Розв'язання
Аби з'ясувати сенс завдання, згадаємо наступне.
1. Електричним струмом називається перенесення електричного заряду в просторі, байдуже, відбувається воно в речовині, чи вакуумі. Тож магнітне поле створюється й визначається не провідним тілом, а впорядкованим рухом у ньому зарядів-носіїв струму.
2. Індукція магнітного поля провідника є прямо пропорційна силі струму, котра теж прямо пропорційно залежить від дрейфовій швидкості носіїв струму (формула (2.4)).
3. Швидкість руху як така є визначеною не сама по собі, а лише по відношенню до якогось вибраного тіла ([І], п. 1.2), яким у даній задачі є візок.
Отже, нехай вільні електрони впорядковано рухаються провідником із якоюсь швидкістю \(\vec{u}\) і створюють струм І протилежного напрямку, як показано на схематичному рис. 1а. Тоді для спостерігача на нерухомому візку (т. А) вектор індукції магнітного поля\(\vec{B}\) за правилом правого гвинта є напрямлений "від нас" і має прямо пропорційний до величини u модуль:
$B\sim u$
Коли ж візок почне рухатись так, як сказано в умові, для спостерігача впорядкований рух електронів припиниться, й вони більше не створюватимуть магнітне поле. Але натомість у протилежному напрямі почнуть зі швидкістю \(\vec{V}=-\vec{u}\) рухатися й створювати магнітне поле позитивно заряджені іони провідника (рис. 1б). При цьому, позаяк кількості та величини заряду іонів і вільних електронів є однакові, створювані ними поля будуть збігатися:
\(\vec{B}^{\prime}=\vec{B}\).
Зауважимо, що отриманий результат залишається чинним при будь-якій швидкості та напрямі руху візка вздовж провідника. Радимо переконатись у цьому самостійно за допомогою формули додавання швидкостей з механіки ([І], п. 1.2)
Задача 3.2. Довгий прямий дріт зі струмом зігнуто під прямим кутом.
Визначити
напрям магнітного поля на лінії однієї з половин провідника.
Розв'язання
На рис. 2 показано частину провідника та певну точку А, в якій належить визначати напрям магнітного поля.
Згідно з принципом суперпозиції, індукція поля всього провідника \(\vec{B}_{0}\) дорівнює сумі індукцій полів його частин:
\(\vec{B}_{0}=\vec{B}_{1}+\vec{B}_{2}\).
При цьому для прямого провідника зі струмом вектор індукції магнітного поля в будь-якій точці має бути перпендикулярним до площини, в якій лежать ця точка та провідник, і спрямованим за правилом правого гвинта (п. 1.1). Тому в точці А вектор індукції поля вертикальної сторони кута (нехай це буде \(\vec{B}_{1}\)) є спрямований "на нас". А ось для горизонтальної сторони та точки А ніякої спільної площини, тож і можливого напряму поля, не існує. Це означає, що на лінії прямого струму індукція створюваного ним магнітного поля дорівнює нулю. Отже для горизонтальної частини провідника маємо \(\vec{B}_{2}\)= 0, і \(\vec{B}_{0}=\vec{B}_{1}\).
Таким чином, маємо наступну відповідь:
магнітне поле зігнутого під кутом прямого провідника на лінії однієї зі сторін спрямовано перпендикулярно до площини кута ''до нас''.
Задача 3.3
Магнітне поле створюється двома довгими розташованими на деякій відстані один від одного прямими провідниками зі струмом.
Визначити
вектор індукції \(\vec{B}_{0}\) поля у віддалених від кожного з них на таку саму відстань точках, якщо в них індукція поля одного провідника B = 0,1 мТл. Розглянути випадки, коли напрями струмів: а) однакові і б) протилежні.
|
Дано: B = 0,1 Тл
|
|
\(\vec{B}_{0}\) - ?
|
Розв'язання
На рис. 3 показано точки перетину K, L провідників із перпендикулярною площиною та точку M, у якій належить визначати вектор \(\vec{B}_{0}\), який за принципом суперпозиції (3.2) дорівнює
| \(\vec{B}_{0}=\vec{B}_{1}+\vec{B}_{2}\), |
(1) |
де \(\vec{B}_{1}\) і \(\vec{B}_{2}\) – вектори індукції поля, яке створює в т. М  кожен із провідників окремо. При цьому за умовою задачі складові вектори мають однакові модулі В й за правилом правого гвинта спрямовані перпендикулярно до відповідних сторін рівностороннього трикутника ΔКLМ .
кожен із провідників окремо. При цьому за умовою задачі складові вектори мають однакові модулі В й за правилом правого гвинта спрямовані перпендикулярно до відповідних сторін рівностороннього трикутника ΔКLМ .
а). Очевидно, що при однаковому напрямку струму в провідниках (рис. 3 а) кут між векторами \(\vec{B}_{1}\) і \(\vec{B}_{2}\) складає 60°. Отже, вектор \(\vec{B}_{0}\) є паралельним до прямої K — L і має модуль
\({B}_{0}=2B\cos{30}^{\circ}=B\sqrt{3}\approx\) 0,17 Тл.
б). При протилежних напрямках струмів (рис. 3 б) указаний кут між векторами дорівнює 120°, тож результуючий вектор є перпендикулярний до напрямку K — L і має модуль
\(B_{0}=2B\cos{60^{\circ}}=0,1\) Тл.
На двох довгих прямих ізольованих провідниках із однаковим струмом у різний спосіб роблять "петлі"однакового розміру і форми. При цьому індукція магнітного поля в центрі петлі, відповідно, складає Bа = 400 мкТл і Bб = 200 мкТл.
Визначити
індукцію магнітного поля, що створюється в цій точці прямою (${{B}_{-}}$) і викривленою (${{B}_{0}}$) частиною провідника окремо.
|
Bа = 400 мкТл Bб = 200 мкТл |
|
${{B}_{-}}$ - ? ${{B}_{о}}$ - ? |
Розв'язання
Форму петель показано на рисунку.
За принципом суперпозиції індукція магнітного поля провідника в центрі петлі дорівнює сумі індукцій полів, створюваних окремо прямою та вигнутою частиною:
${\vec{B}}$ = ${{\vec{B}}_{–}}$ + ${{\vec{B}}_{о}}$.
При цьому вектори ${{\vec{B}}_{–}}$ в обох випадках однакові, а от ${{\vec{B}}_{о}}$ при однакових модулях мають протилежні напрямки: у випадку а) "до нас", а у випадку б) "від нас". Отже, модулі вектора індукції результуючого поля складають, відповідно,
${{B}_{а}}$ = ${{B}_{-}}$ + ${{B}_{о}}$;
${{B}_{б}}$ = ${{B}_{-}}$ – ${{B}_{о}}$.
Звідси дістаємо наступну відповідь:
${{B}_{-}}$ = $\frac{{{B}_{а}}+{{B}_{б}}}{2}$ =300 мкТл; ${{B}_{о}}$ = $\frac{{{B}_{а}}-{{B}_{б}}}{2}$ = 100 мкТл .
В отриманій відповіді впадає в око, що петля із струмом створює в центрі поле, котре є всього втричі слабіше за поле несумірного з нею за довжиною прямого провідника. Це пояснюється тим, що всі ділянки петлі є розташовані на порівняно невеликій відстані від центра, тоді як для прямої частини окремі ділянки при переміщенні від центра стрімко віддаляються від нього, і їхній вклад в індукцію поля швидко стає неістотним.
Рух заряджених частинок у магнітному полі
≈
|
Особливістю задач даної теми є те, що рух зарядів в магнітному полі є рівномірний і, за винятком руху вздовж напрямку поля, криволінійний. За наявності ще й електричного поля слід розглянути віртуальний рух частинки в кожному з полів окремо, а потім "синтезувати" реальний рух. |
У наведених далі задачах по умовчанню поля приймаються за однорідні, й при розрахунках g = 10 м/с2.
Задача 3.5. Авіалайнер із розмахом крил l = 20 м горизонтально пролітає над полюсом зі швидкістю v = 900 км/год. Прийнявши, що магнітне поле Землі в зоні польоту є вертикальним і має індукцію B = 60 мкТл, визначити: а) різницю потенціалів U на кінцях крил; б) покази підключеного до них міліамперметра I із внутрішнім опором R = 0,5 Ом.
Задача 3.6. Електрон влітає в смугу взаємно перпендикулярних електричного (E = 10 кВ/м) та магнітного (B = 10 мТл) полів. Визначити найменшу величину та напрямок швидкості електрона, при яких поля не впливатимуть на його подальший рух.
Задача 3.7. На гладку горизонтальну поверхню, що знаходиться в горизонтальних взаємно перпендикулярних електричному Е = 10 В/см й магнітному В = 20 мТл полях, кладуть і без поштовху відпускають кульку з масою m = 10 мг і зарядом q = 50 мкКл. Відтак кулька через деякий час відривається від поверхні. Визначити, яку відстань S проходить кулька до відриву.
Задача 3.8. Протон, який пройшов прискорювальну напругу U = 100 В, по нормалі входить і наскрізь пролітає плоску смугу паралельного до її поверхонь магнітного поля з індукцією B = 5 мТл. Визначити, на якій відстані S від точки входження та під яким кутом φ протон вийде зі смуги, якщо її товщина d = 25 см .
Задача 3.9. У вільному просторі, в якому зі швидкістю v = 0,5 Мм/с рухається протон (питомий заряд qп = (e/m) дорівнює 9,58·107 Кл/кг), "вмикають" перпендикулярні до його руху та однаково спрямовані електричне (E = 2 кВ/м) і магнітне (B = 10 мТл) поля. Визначити: А) прискорення протона; Б) параметри траєкторії його подальшого руху .
Задача 3.10. Прискорений напругою U = 400 В протон (питомий заряд qп = (e/m) дорівнює 9,58·107 Кл/кг) по нормалі влітає в зону паралельних електричного (Е = 20 В/cм) та магнітного (В = 20 мТл) полів із паралельною до них плоскою межею. Визначити відстань L від точки входження та швидкість v і кут виходу $\vartheta$ протона з полів.
Задача 3.11. Металевий стрижень довжиною l = 25 см, що знаходиться в магнітному полі В = 100 мТл, обертається навколо одного кінця з кутовою швидкістю ω = 2 рад/с в перпендикулярній до напряму поля площині. Визначити напругу U (різницю потенціалів) на кінцях стрижня.
Задача 3.5. Авіалайнер із розмахом крил d = 20 м горизонтально пролітає над полюсом зі швидкістю v = 900 км/год. Прийнявши, що магнітне поле Землі в зоні польоту є вертикальним і має індукцію B = 60 мкТл,
визначити:
а) різницю потенціалів U на кінцях крил;
б) покази підключеного до них міліамперметра I із внутрішнім опором R = 0,5 Ом.
|
Дано: d = 20 м v = 900 км/год B = 60 мкТл R = 0,5 Ом |
|
U - ? I - ? |
Розв'язання
а). При горизонтальному польоті у вертикальному магнітному полі Землі біля полюсу на вільні електрони діє магнітна сила (формула 3.3а), котра створює рівні за величиною й протилежні за знаком надлишкові (''індуковані'') заряди на кінцях крил і відповідне електричне поле ${{\vec{E}}}$ всередині, як схематично показано на рисунку. Це поле нівелює дію магнітного поля ${{\vec{B}}}$, отже, відповідно до формул (1.2) і (3.1а), електрична сила, що діє на електрон, у кожній точці зрівноважує магнітну: 
|
${{\vec{F}}_{е}}$= – ${{\vec{F}}_{m}}$ $\Rightarrow $ $E=vB$. |
|
За умовою магнітне Землі є однорідним, а швидкість літака – сталою. В такому разі величина E в усіх точках однакова й не змінюється з часом. Отже, шукана різниця потенціалів (напруга) на кінцях крил задовольняє умову (1.20) і складає
| $U=vBd$ = 30 мВ. |
|
б). Це завдання є тривіальним. Справді, в крилах і підключених до них провідниках із міліамперметром на електрони діють однакові за напрямом і величиною магнітні сили, що унеможливлює в утвореному замкненому контурі циркуляцію заряду, себто — електричний струм. Отже,
| I = 0. |
|
Задача 3.6. Електрон влітає в смугу взаємно перпендикулярних електричного (E = 10 кВ/м) та магнітного (B = 10 мТл) полів.
Визначити,
найменшу величину та напрямок швидкості електрона, при яких поля не впливатимуть на його подальший рух.
|
Дано: E = 10 кВ/м B = 10 мТл |
|
\(\vec{v}\) - ? |
Розв'язання
Задля зручності зв'яжемо з електроном систему координат XOZ, в якій поля \(\vec{B}\) і \(\vec{E}\) спрямован0, як на рис. 6.
Аби електрон рухався з незмінною за величиною й напрямом швидкістю \(\vec{v}\), сили, що діють на нього з боку електричного та магнітного полів мають бути компенсовані:
|
\(\vec{F}_{е}\) = –\(\vec{F}_{м}\) \(\Rightarrow\) \({F}_{е}\) = \({F}_{м}\). |
(1) |
Тож, відповідно до правила правого гвинта, що визначає напрям магнітної сили, вектор швидкості електрона \(\vec{v}\) має лежати в площині XOZ і в загальному випадку складати якийсь кут α з вектором \(\vec{B}\). Тож для необхідної швидкості електрона за формулами (1.2) і (3.3) маємо:
\(eE=evB\sin\alpha\) \(\Rightarrow\) \(v=\frac{E}{B\sin\alpha}\).
Звідси очевидно, що величина v, як вимагає умова, буде мінімальною, коли електрон влетить перпендикулярно до площини полів із швидкістю
\(v=\frac{E}{B}\) = 106 м/с.
Задача 3.7. На гладку горизонтальну поверхню, що знаходиться в горизонтальних і взаємно перпендикулярних електричному (Е = 5 В/см) та магнітному (В = 20 мТл) полях, кладуть і без поштовху відпускають кульку масою m = 10 мг і зарядом q = 50 мкКл. Відтак кулька через деякий час відривається від поверхні.
Визначити,
яку відстань S проходить кулька до відриву.
|
Дано: Е = 5 В/см В = 20 мТл m = 10 мг q = 50 мкКл |
|
S - ? |
Розв'язання

На кульку після вивільнення, крім сили тяжіння $m\vec{g}$ та електричної ${{\vec{F}}_{e}}$ діє ще й магнітна сила ${{\vec{F}}_{m}}$. Ця сила при показаній на рис. 7 взаємній орієнтації полів за правилом правого гвинта (п. 1.1) є спрямована вертикально вгору і при певній швидкості кульки може спричинити її відрив від опори. Відповідно до формули (3.1), це може статися, коли
| $v=\frac{mg}{qB}$. |
(1) |
Рух кульки відбувається під дією однорідного електричного поля і є рівноприскореним. Отже, необхідної для відриву швидкості кулька набуде на відстані S, яка задовольняє відоме співвідношення механіки ( [І], ф-ла (1.19))
| $S=\frac{{{v}^{2}}}{2a}$ |
(2) |
і, враховуючи вираз (1),
| $S=\frac{{{m}^{2}}{{g}^{2}}}{2{{q}^{2}}{{B}^{2}}a}$ |
(3) |
де a – прискорення кульки, котре створюється електричною силою Fe = qE і за другим законом Ньютона дорівнює
| $a=\frac{qE}{m}$ |
|
Отже, відстань, на якій кулька відірветься від поверхні, дорівнює
| $S=\frac{{{m}^{3}}{{g}^{2}}}{2{{q}^{3}}{{B}^{2}}E}$. |
|
Обчислення дають
| S = 2 м. |
|
Задача 3.8. Протон, який пройшов прискорювальну напругу U = 100 В, по нормалі входить і наскрізь пролітає плоску смугу паралельного до її поверхонь магнітного поля з індукцією B = 5 мТл.
Визначити,
на якій відстані S від точки входження та під яким кутом φ протон вийде зі смуги, якщо її товщина d = 25 см.
|
Дано: U = 100 В B = 5 мТл = 5·10-3 Тл d = 25 см = 0,25 м |
|
S - ? φ - ? |
Розв'язання

Позаяк протон влітає в смугу перпендикулярно до її поверхні, тож і напрямку магнітного поля, далі він рухається по дузі кола певного радіуса R (див. п. 1.2) з центром О на передній стінці смуги, як показано на рис. 8. Отже, шукана відстань S дорівнює довжині основи АС рівнобічного трикутника ОАС з бічною стороною R, а кут виходу φ збігається із кутом при вершині цього трикутника, позаяк його сторони є перпендикулярні до векторів ${{\vec{v}}_{0}}$ і ${{\vec{v}}}$. При цьому величину R можна знайти за формулою (3.4) через задану індукцію магнітного поля В, відомий питомий заряд протона qп та швидкість його входження в смугу v, котра залежить від прискорювальної напруги U. Через це відповіді задачі можна знайти з наступних співвідношень між показаними на рис. 8 характеристиками траєкторії протона:
|
$\frac{d}{S}=\cos \frac{\varphi }{2}$; |
(1) |
|
$\frac{S}{2R}=\sin \frac{\varphi }{2}$. |
(2) |
А саме, піднісши до квадрата та почленно додавши записані рівності, отримаємо біквадратне рівняння
| ${{\left( \frac{d}{S} \right)}^{2}}+{{\left( \frac{S}{2R} \right)}^{2}}=1\quad \Rightarrow \quad {{S}^{4}}-4{{R}^{2}}{{S}^{2}}+4{{R}^{2}}{{d}^{2}}=0$ |
(3) |
одним із коренів якого є шукана величина S. Аби виокремити цей корінь, візьмемо до уваги, що радіус траєкторії протона має задовольняти умову R ≥ d, а відстань S ≤ $\sqrt{2}R$, інакше протон не подолає смугу поля. В такому разі
| S = R$\sqrt{2\left( 1-\sqrt{1-{{\left( {d}/{R}\; \right)}^{2}}} \right)}$. |
(4) |
Отже, аби знайти відстань між точками входу та виходу протона зі смуги, треба спершу обчислити радіус його траєкторії R формула (3.4). Потрібну для цього швидкість протона v знайдемо через його кінетичну енергію, що дорівнює роботі прискорювального електричного поля (формула 1.13):
$\frac{mv_{0}^{2}}{2}=eU$ \(\Rightarrow\) ${{v}_{0}}=\sqrt{2{{q}_{п}}U}$
і, врахувавши формулу (3.4) та значення qп = 9,58·107 Кл/кг , отримаємо
| $R=\frac{1}{B}\sqrt{\frac{2U}{{{q}_{п}}}}$ = 29 см. |
|
Підставивши цу значення у вираз (4), знайдемо наступну величину відстані між точками входу та виходу протона із смуги магнітного поля:
S = 28,5 см,
Відтак із з виразу (1) знайдемо і кут вильоту протона зі смуги:
$\varphi =2\cdot \arccos \frac{d}{S}$ ≈ 57°.
Задача 3.9.
У вільному просторі, в якому зі швидкістю v = 0,5 Мм/с рухається протон (питомий заряд qп = (e/m) = 9,58·107 Кл/кг), "вмикають" перпендикулярні до його руху та однаково спрямовані електричне (E = 2 кВ/м) і магнітне (B = 10 мТл) поля.
Визначити:
А) прискорення протона;
Б) параметри траєкторії його подальшого руху.
|
Дано: v = 0,5 Мм/с = 5·105 м/с E = 2 кВ/м = 2·103 В/м
B = 10 мТл = 10-2 Тл
q/m = 9,58·107 Кл/кг
|
|
a - ?
R - ? h - ?
|
Розв'язання
При ввімкненні полів на протон почнуть діяти взаємно перпендикулярні магнітна \(\vec{F}_{м}\) і електрична \(\vec{F}_{е}\) сили (рис.9). Тож протон буде рівномірно рухатися по колу в перпендикулярній до напрямку полів площині під дією магнітної сили (див. п. 1.2) й одночасно прискорено рухатись уздовж полів під дією електричної сили (розділ І, п. 1.1). При цьому електрична сила не буде впливати на обертальну, а магнітна – на поступальну складову руху протона. Як наслідок, він буде рухатись уздовж полів по гвинтовій лінії з постійним радіусом кривини й змінним кроком, як схематично показано на рис. 9-1.
А). Згідно зі сказаним, прискорення протона \(\vec{a}\) складається з двох незалежних компонент електричної (\(\vec{a}_{1})\) і магнітної \(\vec{a}_{2}\), тож
\(\vec{a}\) = \(\vec{a}_{1}\) + \(\vec{a}_{2}\) $\Rightarrow $ $a=\sqrt{a_{1}^{2}+a_{2}^{2}}$,
де за другим законом Ньютона та формулами (1.2) і (3.3а)
|
${{a}_{1}}={{q}_{п}}E,\quad {{a}_{2}}={{q}_{п}}vB$. |
(1) |
Отже, шукане прискорення протона
$a={{q}_{п}}\sqrt{{{E}^{2}}+{{\left( vB \right)}^{2}}}\approx 5,2\cdot {{10}^{11}}$ м/с2.
 Б). Радіус витка гвинтової лінії, по якій рухається протон, визначається формулою (3.4):
Б). Радіус витка гвинтової лінії, по якій рухається протон, визначається формулою (3.4):
$R=\frac{v}{{{q}_{п}}B}$ = 52 см.
Кроком h гвинтової лінії називається зазор між витками, який звичайно дорівнює відстані між точками дотику сусідніх витків із будь-якої паралельною до осі гвинта прямою, приміром, віссю OZ (рис. 6-1). Але в даній задачі через дію на протон електричного поля крок буде змінюється від витка до витка й залежатиме від положення вказаної дотичної лінії. Тож будемо відміряти його від початкового положення протона. В такому разі для n-го витка крок hn дорівнює різниці відстаней, які протон проходить у напрямку електричного поля за проміжки часу tn = nT і tn-1 = (n–1)T, де T – період обертання протона по трєкторії. Тож згідно з відомою формулою кінематики ([І], ф-ла (1.17)) отримуємо:
${{h}_{n}}=\frac{{{a}_{1}}{{T}^{2}}}{2}\left( {{n}^{2}}-{{\left( n-1 \right)}^{2}} \right)$
або
${{h}_{n}}={{h}_{1}}\left( 2n-1 \right)$,
де
${{h}_{1}}=\frac{{{a}_{1}}{{T}^{2}}}{2}$
– початковий крок, який з урахуванням виразу (1) і формули (3.5а) дорівнює
| ${{h}_{1}}=\frac{2{{\pi }^{2}}E}{{{q}_{п}}{{B}^{2}}}$ = 8 м. |
(2) |
Прискорений напругою U = 400 В протон (питомий заряд (відношення заряду до маси) qп = 9,58·107 Кл/кг) по нормалі влітає в зону паралельних електричного (Е = 20 В/cм) та магнітного (В = 20 мТл) полів із паралельною до них плоскою межею.
Визначити,
відстань L від точки входження та швидкість v і кут виходу $\vartheta$ протона з полів.
|
Дано: Е = 20 В/cм В = 20 мТл U = 400 В qп= 9,58·107 Кл/кг |
|
L- ?, v-?, $\vartheta$-? |
Розв'язання
Оберемо систему координат з початком О в точці входження протона в поля і віссю ОХ, що за напрямом збігається з початковою швидкістю протона $\vec{v}_{0}$, як показано на рис. 10.
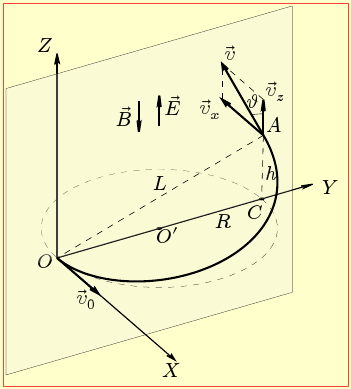
При такому виборі координатної системи умови руху протона при входженні польовій зоні є такі самі, як у Задачі 3.9, тож він почне рухатися навколо напрямку полів по гвинтовій лінії зі змінним кроком. Але через наявність межі (площина YOZ), протон перебуватиме в полях тільки протягом часу t у пів періоду обертання (3.5) навколо напряму полів:
| $t=\frac{\pi }{{{q}_{п}}B}$ |
(1) |
і здійснить тільки половину першого витка траєкторії.
За вказаних умов у кожний момент часу протон під дією магнітного поля обертатиметься із сталою швидкістю v = v0 в паралельній до {XOY} площині по колу радіуса R й одночасно рухатиметься у напрямку осі ОZ під дією електричного поля. При цьому за час t протон зміститься на відстань 2R вздовж осі OY і h в напрямку OZ. Отже шукана відстань між точками входження і виходу складає
| $L=\sqrt{4{{R}^{2}}+{{h}^{2}}}$. |
(2) |
Величину R знайдемо за формулою (3.4), в якій індукцію поля B в умові задано прямо, а поперечну швидкість протона v0 – опосередковано через його початкову кінетичну енергію, що дорівнює роботі прискорювального поля (1.13а):
| $\frac{mv_{0}^{2}}{2}=eU\quad \Rightarrow \quad {{v}_{0}}=\sqrt{2{{q}_{п}}U}$. |
(3) |
Відтак, підставивши це значення у формулу (3.4), дістанемо:
| $R=\frac{1}{B}\sqrt{\frac{2U}{{{q}_{п}}}}$. |
(4) |
Величина h, згідно з формулою кінематикою ([I], ф-ла (1.17)) складає
| $h=\frac{a{{t}^{2}}}{2}$, |
(5) |
де прискорення a створюється електричним полем і за ІІ законом Ньютона та формулою (1.20) дорівнює
|
$a=\frac{eE}{m}={{q}_{п}}E$, |
(6) |
а час руху протона t = (T/2) визначається виразом (1).
Тож, згідно з виразом (5), вертикальне зміщення протона дорівнює
| $h=\frac{{{\pi }^{2}}E}{2{{q}_{п}}{{B}^{2}}}$. |
(7) |
Відтак, обчисливши за формулами (4) і (7) значення R і h, із виразу (2) знайдемо:
$L$ = 38,7 см.
Далі, обчисливши за формулами (6) і (1) вертикальну складову vz = at і врахувавши, що горизонтальна vх = v0, знайдемо швидкість
$v=\sqrt{v_{0}^{2}+v_{1}^{2}}$ = 4,2·105 м/с
та через якусь із тригонометричних функцій – кут виходу виходу протона з полів:
$\vartheta$ = 41,4°.
|
Задача 3.11.  Металевий стрижень ОА (рис.11-1) довжиною l = 25 см, що знаходиться в магнітному полі В = 100 мТл, обертається навколо одного кінця з кутовою швидкістю ω = 2 рад/с в перпендикулярній до напряму поля площині . Визначити напругу U (різницю потенціалів) на кінцях стрижня. |
||||||
Через дію магнітного поля на вільні електрони (розділ ІІІ, п. 1.2) на кінцях Електрична та магнітна сили є протилежно спрямовані й компенсовані. Тож відповідно до (формул (1.2) та (3.3а) в кожній точці стрижня встановлюється стаціонарне електричне поле, напруженість якого на відстані r від осі обертання складає
де B – індукція магнітного поля, ω – кутова швидкість стрижня і v – лінійна швидкість даної точки.  Між напруженістю електричного поля та різницею потенціалів (напругою) існує однозначний зв’язок, який для однорідного поля (${{\vec{E}}}$ = const) виражається співвідношенням (1.20). Але в даній задачі безпосередньо за ним знайти напругу U на кінцях стрижня неможливо, бо напруженість поля E в ньому змінюється від точки до точки, як показано на рис. 11-3. Проте, якщо графік подумки поділити на вузькі смужки шириною Δrі так, аби напруженість Ei в межах однієї смужки можна було вважати однаковою, то за виразом (1.20) напруга на окремій смужці ΔUi ≈ EiΔrі, а на всьому стрижні U ≈ Σ(EiΔrі), що чисельно дорівнює сумарній площі S всіх виділених ділянок на графіку: U ≈ S. Зрозуміло, що при зменшенні ширини смужок точність отриманого виразу буде підвищуватись і в границі Δrі → 0 стане абсолютною. При цьому величина S зрівняється з площею трикутника ΔОАl на графіку. Отже, $U=\frac{1}{2}{{E}_{A}}l$, і, згідно з виразом (1),
|
Провідники зі струмом у магнітному полі
|
Задачі з цієї теми вимагають використання теоретичних відомостей з механіки (див. [І], розділи ІІ, V ). При розрахунках за умовчанням прийнято g = 10 м/с2. |
Задача 3.12. На горизонтальній поверхні, що знаходиться у спрямованому під кутом Θ = 60° до вертикалі магнітному полі з індукцією B = 0,1 Тл, лежить перпендикулярний до напряму поля стрижень масою m = 0,2 кг і довжиною l = 0,3 м. Визначити, за якої найменшої величини струму I у стрижні він почне ковзати при коефіцієнті тертя \(\mu=0,2\).
Задача 3.13. Стрижень довжиною l = 20 см і масою m = 50 г на двох однакових нитках підвісили на одному рівні перпендикулярно до напрямку горизонтального магнітного поля B = 0,2 Тл. Визначити, при якій мінімальній силі струму I0 в стрижні одна з ниток лусне, якщо міцність кожної на розрив F0 = 0,3 Н.
Задача 3.14. Каркас у формі трьох сторін квадрата з мідного (ρ = 8,9 г/см3) дроту перерізом S = 2,8 мм2 вільно підвісили на горизонтальній осі та вмістили у вертикальне магнітне поле з індукцією B = 10 мТл. Визначити кут відхилення \(\varphi\) каркаса від вертикалі при пропусканні по ньому струму I = 50 A.
Задача 3.12. На горизонтальній поверхні, що знаходиться у спрямованому під кутом Θ = 60° до вертикалі магнітному полі з індукцією B = 0,1 Тл, лежить перпендикулярний до напряму поля стрижень масою m = 0,2 кг і довжиною l = 0,3 м.
Визначити,
за якої найменшої величини струму I у стрижні він почне ковзати при коефіцієнті тертя \(\mu=0,2\).
|
Дано: m = 0,2 кг
\(\mu=0,2\)
B = 0,1 Тл
\(\Theta=30^{\circ}\)
|
|
I - ?
|
Розв'язання
Розташування стрижня відносно поля відображає рис. 12 7.
При протіканні струму на стрижень, окрім сил тяжіння \(m\vec{g}\) та нормального тиску \(\vec{N}\) з боку поверхні, діє ще й сила Ампера \(\vec{F}_{A}\) (рис. 12-1 7-1), котра, як зрозуміло з умови, спрямована під кутом Θ до поверхні, тож може спричинити ковзання стрижня.
тяжіння \(m\vec{g}\) та нормального тиску \(\vec{N}\) з боку поверхні, діє ще й сила Ампера \(\vec{F}_{A}\) (рис. 12-1 7-1), котра, як зрозуміло з умови, спрямована під кутом Θ до поверхні, тож може спричинити ковзання стрижня.
Згідно з положеннями механіки ([І], ф-ла (2.14)), мінімальна необхідна для подолання тертя горизонтальна складова сили Ампера FAcosΘ (рис. 12-1) має дорівнювати
|
FcosΘ = μN, |
(1) |

де μ – коефіцієнт тертя і N – нормальна реакція опори, що визначається силою тяжіння mg та вертикальною складовою сили Ампера FAsinΘ. При цьому, залежно від напряму струму, можливі два випадки: струм спрямовано "на нас" (рис.12-1а), або "від нас" (рис.12-1б). Відповідно, реакція опори N та необхідна для подолання тертя сила Ампера FA у випадках а) і б) є різними:
${{N}_{1}}=mg-{{F}_{1A}}\sin \Theta \quad \Rightarrow \quad {{F}_{1A}}=\frac{\mu mg}{\cos \Theta +\mu \sin \Theta }$; |
(2а) |
|
${{N}_{2}}=mg+{{F}_{2A}}\sin \Theta \quad \Rightarrow \quad {{F}_{2A}}=\frac{\mu mg}{\cos \Theta -\mu \sin \Theta }$. |
(2б) |
Тож, зважаючи на формулу (3.8а), отримаємо наступні дві відповіді:
\(I_{1}=\frac{\mu{mg}}{Bl(\cos\Theta+\mu\sin\Theta)}\) ≈ 13,5 A;
\(I_{2}=\frac{\mu{mg}}{Bl(\cos\Theta-\mu\sin\Theta)}\) ≈ 17,1 A.
Наостанку зауважимо таке. Із виразу (2б) видно, що у випадку б) за умови \(\cos\Theta=\mu\sin\Theta\), або
$\operatorname{tg}\Theta =\frac{1}{\mu }$,
величина FA → ∞, тобто ніякий струм не зрушить стрижень з місця. Зрозуміло, що так само буде й з усяким іншим тілом і при будь-якій природі сили, що намагається його пересувати по опорі. Тому величина
$\Theta =\operatorname{arctg}\frac{1}{\mu }$
називається "кутом тертя" і визначає теоретичну межу можливості переміщення вантажів по горизонтальній поверхні штовханням.
Задача 3.13.
Стрижень довжиною l = 20 см і масою m = 50 г на двох однакових нитках горизонтально підвісили перпендикулярно до напрямку горизонтального магнітного поля B = 0,2 Тл.
Визначити,
при якій мінімальній силі струму I0 в стрижні одна з ниток лусне, якщо міцність кожної на розрив F0 = 0,3 Н.
|
Дано: l = 20 см = 0,2 м
m = 50 г = 0,05 кг
F0 = 0,3 Н
B = 0,2 Тл
|
|
I0 - ?
|
Розв'язання

Відповідно до правила правого гвинта та умови задачі, сили натягу ниток \(\vec{F}\), Ампера \(\vec{F}_{А}\) та тяжіння \(m\vec{g}\), що діють на стрижень, є спрямовані вертикально, як показано на рис. 13. Отже, при рівновазі, враховуючи формулу (3.8a),маємо:
\(mg+IlB=2F\).
Якась із ниток порветься при струмі I0, за якого сила натягу сягне граничної можливої величини F = F0. Отже,
\(mg+I_{0}lB=2F_{0}\) \(\Rightarrow\) \(I_{0}=\frac{2F_{0}-mg}{Bl}=2,75\) A.
Задача 3.14.
Каркас у формі трьох сторін квадрата з мідного (ρ = 8,9 г/см3) дроту перерізом S = 2,8 мм2 вільно підвісили на горизонтальній осі та вмістили у вертикальне магнітне поле з індукцією B = 10 мТл.
Визначити
кут відхилення \(\varphi\) каркаса від вертикалі при пропусканні по ньому струму I = 50 A.
|
Дано: S = 3 мм2 = 3·10–6 м2
B = 10 мТл = 10–2 Тл
I = 50 A
|
|
\(\varphi\) - ?
|
Розв'язання
Уведемо позначення m і l для маси та довжини однієї сторони каркаса.
Просторове розташування підвішеного в магнітному полі каркаса зі струмом визначається силами тяжіння та Ампера, що діють на його сторони. В початковому (вертикальному) положенні каркаса магнітне поле, згідно з формулою (3.8), діє тільки на нижню сторону каркаса із перпендикулярною до нього горизонтальною силою \(\vec{F}_{А}\) (рис. 14а), котра відхиляє площину каркаса від вертикалі. При цьому з'являються й сили \(\vec{F}_{А1}\), \(\vec{F}_{А2}\), прикладені до бічних сторін. Але вони є паралельні до осі підвісу (рис. 14б) й зрівноважені, тож не впливають на розташування каркаса. Отож, згідно із статикою ([І], ф-ла (5.4)), каркас відхиляється від вертикалі на кут, при якому сумарний момент сил тяжіння та поперечної до осі обертання OO′ сили Ампера дорівнює нулю.
Для складання потрібного рівняння моментів урахуємо таке. Плечі ОР сил тяжіння (рис.14в), що діють на бічні сторони каркаса, дорівнюють (l·sinφ)/2, (рис. 14в). Відповідно, їхній сумарний момент М1 = 2mg(l/2)·sinφ = mgl·sinφ. Для нижньої сторони плече сили тяжіння OQ є вдвічі більшим, отож її момент М2 = mgl·sinφ. А плече сили Ампера дорівнює lcosα і її момент М3 = FA·lcosφ. Отже, умова рівноваги каркаса М1 + М2 = М3 має вигляд:
FA·lcosφ = 2mglsinφ.
Відтак, виразивши силу Ампера за формулою (3.8) і масу однієї сторони каркаса через густину та об'єм дроту як m = ρlS , отримаємо наступну відповідь:
\(\mathrm{tg}\varphi=\frac{IBl}{2\rho{Slg}}=\frac{IB}{2\rho{Sg}}\).
Обчислення дають:
\(\mathrm{tg}\varphi=1\) \(\Rightarrow\) \(\varphi=\mathrm{arctg}(0,93)=43^{\circ}\).
Явище електромагнітної індукції
При обчисленнях скрізь прийнято g = 10 м/с2.
Задача 3.15. Потік крізь уміщену в однорідне магнітне поле плоску рамку дорівнює \(\Phi=10\) мВб. Визначити середню ЕРС індукції \(\mathcal{\E}_{с}\), яка виникне в рамці при її повороті за час \(\tau=2\) c на кут \(\varphi=180^{\circ}\) навколо осі перпендикулярної до напрямку поля.
Задача 3.16. Перпендикулярну до напрямку магнітного поля B = 100 мкТл прямокутну рамку площею \(S=50\) см2, яка містить N = 100 витків і має опір R = 0,5 Ом, починають обертати з кутовою швидкістю \(\omega = 200\pi\) (рад/с) навколо осі, що проходить через середини протилежних сторін. Визначити залежність I(t) сили струму в рамці від часу та його величину через n = (1/4) оберту.
Задача 3.17. При повороті в магнітному полі перпендикулярної до його напряму дротяної рамки на кут \(\alpha_{1}=180^{\circ}\) навколо осі, що лежить у площині рамки, заряд, який проходить по ній, дорівнює q1 = 3,6 мкКл, а при повороті на деякий кут \(\alpha_{2}\) він складає q2 = 0,9 мкКл. Визначити величину \(\alpha_{2}\).
Задача 3.18. Металевий стрижень довжиною l = 25 см, що знаходиться в магнітному полі В = 100 мТл, обертається навколо одного кінця з кутовою швидкістю ω = 2 рад/с в перпендикулярній до напряму поля площині. Визначити напругу (різницю потенціалів Δφ) на кінцях стрижня.
Задача 3.19. На дві довгі паралельні металеві шини, замкнені з одного боку на резистор R = 100 мОм і вміщені у вертикальне магнітне поле B = 0,5 Тл так, що їхня площина складає кут $\vartheta =20{}^\circ $ з горизонтом, поклали й відпустили провідну поперечку масою m = 20 г. Нехтуючи опором шин і поперечки, визначити, до якої максимальної швидкості vm вона розженеться при зісковзуванні з коефіцієнтом тертя \(\mu=0,3\), якщо відстань між шинами l = 20 см.
Задача 3.20. Обмотка шкільного реостата є щільно намотана в один шар на циліндричну керамічну трубку діаметром D = 8 см і має довжину l = 30 см. Вважаючи магнітне поле обмотки однорідним, визначити її індуктивність L, якщо при струмі I = 1,5 А індукція поля всередині B = 2 мТл.
Задача 3.21. При зміні сили струму в котушці на \(\Delta{I}\) = 1 A енергія її магнітного поля змінилася в n = 4 рази. Визначити, якою була сила струму I1 в котушці.
Задача 3.15
Потік крізь уміщену в однорідне магнітне поле плоску рамку дорівнює \(\Phi=10\) мВб.
Визначити
середню ЕРС індукції \(\mathcal{\E}_{с}\), яка виникне в рамці при її повороті за час \(\tau=2\) c на кут \(\varphi=180^{\circ}\) навколо осі перпендикулярної до напрямку поля.
|
Дано: S = 200 см2 = 2·10-2 м2
\(\Phi=10\) мВб = 10-2 Вб
\(\tau=2\) c
\(\varphi=180^{\circ}\)
|
|
\(\mathcal{\E}_{с}\) - ?
|
Розв'язання
Відповідно до формули (3.11a) та умови задачі середня ЕРС індукції в рамці дорівнює
|
\(\mathcal{\E}_{с}=\frac{\Phi-\Phi_{2}}{\tau}\), |
(1) |

де \(\Phi\) – задане початкове, а \(\Phi_{2}\) – кінцеве значення магнітного потоку крізь рамку. При цьому
$\Phi ={{\Phi }_{0}}\cos \alpha $,
де Ф0 – потік при перпендикулярному розташуванні площини рамки відносно поля, і \(\alpha\) (рис.15 10 показати кут) – початковий кут між нормаллю \(\vec{n}\) до площини рамки та напрямом поля \(\vec{B}\). Відповідно, кінцевий потік
${{\Phi }_{2}}={{\Phi }_{0}}\cos \left( \alpha +180{}^\circ \right)=-\Phi $.
Отже, згідно з виразом (1), шукана середня ЕРС індукції при повороті рамки дорівнює
\(\mathcal{\E}_{с}=\frac{2\Phi}{\tau}=0,1\) В.
Зауваження. При розв'язуванні задачі могло здатися, що при повороті на \(180^{\circ}\) площина рамки займає ідентичне до вихідного кінцеве положення, тож кінцевий потік дорівнює початковому й середня ЕРС індукції \(\mathcal{\E}_{с}=0\). Але це не так, бо магнітний потік крізь рамку є алгебраїчною величиною (див. п.1.4), і має не лише певну абсолютну величину, а й відповідний знак, який відповідно до умови змінюється на протилежний.
Задача 3.16
Перпендикулярну до напрямку магнітного поля B = 100 мкТл прямокутну рамку площею \(S=50\) см2, яка містить N = 100 витків і має опір R = 0,5 Ом, починають обертати з кутовою швидкістю \(\omega = 200\pi\) (рад/с) навколо осі, що проходить через середини протилежних сторін.
Визначити
залежність I(t) сили струму в рамці від часу та його величину I1 через n = (1/4) оберту.
|
Дано: \(S=50\) см2 = 5·10–3 м2
N = 100
\(\omega = 200\pi\ {рад/с}\)
B = 100 мкТл = 10–4 Тл
n = (1/4)
R = 0,5 Ом
|
|
I(t) - ?, I1 - ?
|
Розв'язання
За законом Ома (2.13) сила струму в рамці дорівнює відношенню ЕРС індукції, що визначається законом Фарадея (3.13), до опору рамки:
|
$I(t)=-\frac{N}{R}{{\Phi }_{1}}^{\prime }$, |
(1) |
де ${{\Phi }_{1}}$ – магнітний потік крізь один виток, який за формулою  (3.10) дорівнює
(3.10) дорівнює
\(\Phi_{1}=BS\cos\alpha\).
Отже, і враховуючи, що при обертанні рамки з кутовою швидкістю $\omega $ кут \(\alpha\) (рис. 16 11-1) в довільний момент часу складає \(\alpha=\omega{t}\), маємо:
${{\Phi }_{1}}=BS\cos \omega t$,
тож повний потік крізь рамку (формула (3.12)) дорівнює
\(\Phi=NBS\cos(\omega{t})\),
і, згідно з виразом (1) і враховуючи, що, ${{\left( \cos \omega t \right)}^{\prime }}=-\omega \sin \omega t$, отримуємо шукану залежність струму від часу:
$I(t)=\frac{N\omega BS}{R}\sin \omega t={{I}_{m}}\sin \omega t$
де ${{I}_{m}}=\frac{N\omega BS}{R}$ – максимальна величина струму в рамці, яка за даними умови складає
${{I}_{m}}\approx 63$ мА.
За чверть оберту рамка повертається на 90°, отже
${{I}_{1}}\approx 63$ мА.
Задача 3.17. При повороті в магнітному полі перпендикулярної до його напряму рамки на кут \(\alpha_{1}=180^{\circ}\) навколо осі, що лежить у площині рамки, заряд, який проходить по ній, дорівнює q1 = 3,6 мкКл, а при повороті на деякий кут \(\alpha_{2}\) він складає q2 = 0,9 мкКл.
Визначити
величину \(\alpha_{2}\).
|
Дано: \(\alpha_{1}=180^{\circ}\) \(q_{1}=3,6\) мкКл
\(q_{2}=0,9\) мкКл
|
|
\(\alpha_{2}\) - ?
|
Розв'язання
Очевидною причиною проходження по рамці заряду $q$ є індукційний струм ${{I}_{i}}$, який виникає при зміні магнітного потоку крізь неї внаслідок зміни орієнтації в магнітному полі, тобто – кута $\alpha $. Але потрібна для отримання відповіді залежність $q\left(\alpha \right)$ не є очевидною, бо невідомо, як саме магнітний потік та індукційний струм змінюються з часом. Тому спочатку розглянемо, який заряд $\Delta {{q}_{i}}$ проходить по рамці за довільний малий проміжок часу $\Delta {{t}_{i}}$, врахувавши, що за означенням (2.1а)
$\Delta {{q}_{i}}={{I}_{i}}\Delta {{t}_{i}}$,
де ${{I}_{i}}$ – середня сила індукційного струму, що за законом Ома (2.13) визначається опором рамки $R$ і середньою ЕРС індукції, котра наближено виражається формулою (3.11а):
${{\E}_{i}}\approx -\frac{\Delta {{\Phi }_{i}}}{\Delta {{t}_{i}}}$.
Отже,
${{I}_{i}}\approx -\frac{1}{R}\frac{\Delta {{\Phi }_{i}}}{\Delta {{t}_{i}}}$
і
$\Delta {{q}_{i}}\approx -\frac{\Delta {{\Phi }_{i}}}{R}$.
Відповідно, заряд, що проходить по контуру за весь час повороту
$q=\sum{\Delta {{q}_{i}}}$ $\Rightarrow $ $q=\frac{\sum{\Delta {{\Phi }_{i}}}}{R}=\frac{{{\Phi }_{0}}-\Phi }{R}$,
де ${{\Phi }_{0}}$ і ${\Phi }$ – початкове та кінцеве значення потоку при повороті контуру.
Таким чином, відповідно до формули (3.10а) і, враховуючи, що $\cos {{\alpha }_{1}}=-1$, маємо:
$\frac{{{q}_{2}}}{{{q}_{1}}}=\frac{1-\cos {{\alpha }_{2}}}{2}$
звідки для заданих значень заряду отримуємо наступну відповідь:
$\cos {{\alpha }_{2}}=\frac{1}{2}\quad \Rightarrow \quad {{\alpha }_{2}}$ = 60°.
Задача 3.18. Металевий стрижень довжиною l = 25 см, що знаходиться в магнітному полі В = 100 мТл, обертається навколо одного кінця з кутовою швидкістю ω = 2 рад/с в перпендикулярній до напряму поля площині. Визначити напругу (різницю потенціалів Δφ) на кінцях стрижня.
|
Дано: l = 25 см В = 100 мТл ω = 2 рад/с |
|
Δφ – ? |
Розв'язання

Вище (Зад. 3.11) цю задачу вже було розв'язано прямим розглядом дії магнітного поля на рухомі заряди. Але зручніше зробити це на основі закону електромагнітної індукції (ЕМІ) (розділ ІІІ, п. 1.4). А саме. Уявімо, що кінець А стрижня ковзає по дротяному кільцю радіуса l, а нерухомий кінець О з'єднано провідником з якоюсь точкою С , рис 18. (замість наведеного тут рис. 12 взяти скоригований рис. із зад. 3.11 і провести в ньому ще один радіус ОС по ходу руху), так що утворюється провідний контур АОС, в якому через зміну площі при обертанні стрижня виникає ЕРС та індукційний струм. В такому разі стрижень постає як джерело струму з різницею потенціалів Δφ на полюсах (кінцях), котра підлягає визначенню.
За законом Ома в замкненому електричному колі різниця потенціалів на полюсах джерела відрізняється від ЕРС (див. розділ ІІ, ф-ла (2.11)). Але в нашому удаваному колі (контурі АОС) ніякого струму насправді немає, тому шукана різниця потенціалів Δφ = φА – φО збігається з ЕРС індукції й за виразом (3.11а) та формулою (3.10а)) складає
$\frac{S}{T}=\frac{\Delta S}{\Delta t}\quad \Rightarrow \quad \frac{\Delta S}{\Delta t}=\frac{1}{2}\omega {{l}^{2}}$.
Підставивши це значення у вираз (1), дістанемо наступну відповідь:
$\Delta \varphi =\frac{1}{2}B\omega {{l}^{2}}$ = 6,25 мВ.
Задача 3.19.
На дві довгі паралельні металеві шини, замкнені з одного боку на резистор R = 0,01 Ом і вміщені у вертикальне магнітне поле B = 0,5 Тл так, що їхня площина складає кут $\vartheta =30{}^\circ $ з горизонтом, поклали й відпустили провідну поперечку масою m = 20 г. Нехтуючи опором шин і поперечки,
визначити,
до якої максимальної швидкості vm вона розженеться при зісковзуванні з коефіцієнтом тертя \(\mu=0,1\), якщо відстань між шинами l = 20 см.
|
Дано: l = 20 см = 0,2 м
R = 100 мОм= 0,1 Ом
B = 0,5 Тл
$\vartheta =20{}^\circ $
m = 20 г = 0,02 кг
\(\mu = 0,3\)
|
|
vm - ?
|
Розв'язання
Шини з резистором і поперечка утворюють замкнений провідний контур площею ${S}$ (рис. 19а 14-1а), магнітний потік крізь  який $\Phi =BS\cos \vartheta $ при зісковзуванні поперечки змінюється з часом і створює відповідну ЕРС ${{\E}_{i}}$ та індукційний струм ${{I}_{i}}$. Через це на поперечку, крім сил тяжіння $m\vec{g}$ та тертя ${{\vec{F}}_{т}}$, діє сила Ампера ${{\vec{F}}_{A}}$ (п. 1.3), котра відповідно до правила Ленца (п. 1.4) є гальмівною й спрямована, як показано на рис.19б.
який $\Phi =BS\cos \vartheta $ при зісковзуванні поперечки змінюється з часом і створює відповідну ЕРС ${{\E}_{i}}$ та індукційний струм ${{I}_{i}}$. Через це на поперечку, крім сил тяжіння $m\vec{g}$ та тертя ${{\vec{F}}_{т}}$, діє сила Ампера ${{\vec{F}}_{A}}$ (п. 1.3), котра відповідно до правила Ленца (п. 1.4) є гальмівною й спрямована, як показано на рис.19б.
Після вивільнення поперечка починає рухатися з прискоренням, тож швидкість зміни потоку зростає з часом. Тому ЕРС індукції і сила індукційного струму, тож і гальмівна сила Ампера (ф-ла 3.8а), що діє на поперечку, будуть поступово збільшуватись, а прискорення – зменшуватись, аж поки зовсім зникне. Відтак поперечка буде рівномірно рухатись із набутою на цей момент максимальною швидкістю vm.
Таким чином, умовою максимуму швидкості поперечки є компенсація проєкцій прикладених до поперечки сил на напрям руху (вісь Х). Отже (див. рис. 19 б),
|
$mg\sin \vartheta ={{F}_{т}}+{{F}_{A}}\cos \vartheta $ |
(1) |
З механіки ([І], п. 2.3) відомо, що
${{F}_{т}}=\mu N$,
де сила нормальної реакції опори ${N}$, яка в нашому випадку зрівноважує нормальні складові (проєкції на вісь Y) сил тяжіння та Ампера і дорівнює
$N=mg\cos \vartheta +{{F}_{A}}\sin \vartheta $.
Таким чином,
|
${{F}_{т}}=\mu mg\cos \vartheta +\mu {{F}_{A}}\sin \vartheta $. |
(2) |
Підставивши це значення у вираз (1), після елементарних перетворень отримаємо:
|
${{F}_{A}}=mg\cdot \frac{\sin \vartheta -\mu \cos \vartheta }{\cos \vartheta +\mu \sin \vartheta }$, |
(3) |
звідки зможемо визначити індукційний струм, а відтак і шукану максимальну швидкість поперечки. А саме, згідно з отриманим виразом і формулою (3.8а),
${{I}_{i}}=\frac{mg}{lB}\cdot \frac{\sin \vartheta -\mu \cos \vartheta }{\cos \vartheta +\mu \sin \vartheta }$,
а за законами Ома (2.13) та Фарадея (3.11)
${{I}_{i}}=\frac{{{\Phi }'}}{R}$,
де $R$ – опір контуру, а \({{\Phi }'}\) – швидкість зміни потоку крізь нього, котра відповідно до формули (3.10), визначається індукцією поля ${B}$ та швидкістю зміни площі зафарбованого прямокутника на рис. 19 б), що дорівнює добутку відстані між шинами на швидкість руху поперечки: ${S}'={lv}$. Тож маємо наступний вираз сили індукційного струму через поперечку
$I=\frac{Blv\cos \vartheta }{R}$,
і після підстановки його в рівність (4) та елементарних перетворень отримаємо загальну відповідь задачі:
$v=\frac{mgR}{{{B}^{2}}{{l}^{2}}}\cdot \frac{\operatorname{tg}\vartheta -\mu }{\cos \vartheta +\mu \sin \vartheta }$.
Обчислення дають
v = 12 см/с.
Задача 3.20.
Обмотка шкільного реостата є щільно намотана в один шар на циліндричну керамічну трубку діаметром D = 8 см і має довжину l = 30 см. Вважаючи магнітне поле обмотки однорідним,
визначити
її індуктивність L, якщо при струмі I = 1,5 А індукція поля всередині B = 2 мТл.
|
Дано: d = 1 мм = 10-3 м
D = 8 см = 8·10-2 м
l = 30 см = 0,3 м
I = 1,5 А
B = 2 мТл = 2·10-3 Тл
|
|
L - ?
|
Розв'язання
За означенням (3.14) та формулою (3.12) індуктивність обмотки
$L=\frac{N{{\Phi }_{1}}}{I}$,
де \(\Phi_{1}\) – магнітний потік крізь один виток і N – кількість витків в обмотці, яка дорівнює
\(N=\frac{l}{d}\).
За умовою поле всередині обмотки є однорідне, тобто скрізь однакове за величиною й напрямом. Отже, за формулою (3.10a)
${{\Phi }_{1}}=B\frac{\pi {{D}^{2}}}{4}$,
де $\left( \pi {{D}^{2}}/4 \right)=S$ – площа витка.
Відтак, підставивши вирази N та \(\Phi_{1}\) у вихідну формулу, дістанемо загальну відповідь:
\(L=\frac{\pi{l}D^{2}B}{4dI}\)
і після обчислень
L= 2 мГн.
Задача 3.21.
При зміні сили струму в котушці на $\Delta I$ = 1 A енергія її магнітного поля змінилася в n = 4 рази.
Визначити,
якою була сила струму ${{I}_{1}}$ в котушці.
|
Дано: ΔІ = 1 А n = 4 |
|
І1 - ? |
Розв'язання
Відповідь задачі можна знайти одразу, бо крім заданої різниці кінцевого та початкового значень струму
|
$\left| {{I}_{2}}-{{I}_{1}} \right|=\Delta I$, |
(1) |
в умові через відношення енергій W магнітного поля (формула 3.16), опосередковано задано і їхнє відношення:
|
$\frac{{{I}_{2}}}{{{I}_{1}}}=\sqrt{\frac{{{W}_{2}}}{{{W}_{1}}}}$. |
(2) |
Але, позаяк не вказано, як змінюється струм, треба окремо розглядати два випадки: А) струм збільшується і Б) струм зменшується.
А) Якщо струм збільшується, маємо:
$\left\{ \begin{align} & {{I}_{2}}={{I}_{1}}+\Delta I \\ & \frac{{{I}_{2}}}{{{I}_{1}}}=\sqrt{n} \\\end{align} \right.\quad \quad \Rightarrow \quad \quad {{I}_{1}}=\frac{\Delta I}{\sqrt{n}-1}$.
Б) При зменшенні струму
$\left\{ \begin{align} & {{I}_{2}}={{I}_{1}}-\Delta I \\ & \frac{{{I}_{2}}}{{{I}_{1}}}=\frac{1}{\sqrt{n}} \\\end{align} \right.\quad \quad \Rightarrow \quad \quad {{I}_{1}}=\frac{\sqrt{n}\Delta I}{\sqrt{n}-1}$.
Числові відповіді:
${{I}_{1}}$ = (1 А, або 2 А).
3. Задачі для самостійної роботи
|
Рівень А |
|
|
3.22. |
Індукція магнітного поля, що створюється струмом у намотаному на дві рознесені котушки дроту, в певній точці становить ${{\vec{B}}_{0}}$. Якою буде індукція \({{\vec{B}}}\) при перемотуванні дроту в напрямку струму зі швидкістю в 1,5 раза більшою за швидкість напрямленого руху електронів усередині провідника? [${{\vec{B}}}$ = ${{\vec{B}}_{0}}$] |
|
3.23. |
Два взаємно перпендикулярні круглі кільця зі струмом зіставлені центрами. Визначити індукцію магнітного поля в центрі кілець, якщо кожне створює в ньому поле 495 мкТл. [700 мкТл] |
| 3.24. |
Визначити індукцію магнітного поля в центрі дротяного квадрата, що підключений до джерела струму протилежними вершинами, якщо кожна сторона створює в центрі поле з індукцією В. [0] |
| 3.25. |
Куб, що спаяний з однакових дротин, протилежними вершинами підключено до джерела струму. Визначити індукцію магнітного поля в центрі куба В0, якщо одна сторона створює в ньому магнітне поле з індукцією В1. [В0 = 0] |
| 3.26. |
Кожен із двох довгих паралельних дротів із однаковим струмом створює в місці розташування іншого магнітне поле з індукцією В. Визначити індукцію поля посередині між дротами за умови, що їхні струми спрямовані: а) однаково; б) протилежно. [0; 4В] |
|
Довгий прямий провідник із струмом у деякій точці створює магнітне поле з індукцією ${{\vec{B}}_{0}}$. Якою вона стане, якщо провідник перегнути під прямим кутом так, аби ця точка опинилась на продовженні однієї із сторін кута? $\left[ {{{\vec{B}}}_{0}}/2 \right]$ |
|
| 3.28. |
Електрон (m = 9,1·10–31 кг, q = 1,6·10–19 Кл) із швидкістю 106 м/с влітає в магнітне поле й рухається далі по колу радіуса 5 мм. Знайти індукцію поля В. [5,7 мТл] |
| 3.29. |
Перпендикулярно до магнітного поля з індукцією 10 мТл влітає електрон, який має кінетичну енергію 30 кеВ. Визначити радіус кривини траєкторії подальшого руху електрона. [58 мм] |
| 3.30. |
Визначити прискорення електрона, який рухається зі швидкістю 1Мм/с по колу в однорідному магнітному полі з індукцією 10 Тл. Питомий заряд електрона 1, 76·1011 Кл/кг. [1, 76·1015 м/с2] |
| 3.31. |
Визначити питомий заряд частинки, яка рухається по колу радіуса 41,5 мм зі швидкістю 105 м/с в магнітному полі з індукцією 90 мТл . [4,82·107 Кл/кг] |
| 3.32. |
У нерухомому провіднику зі струмом, який вміщено в магнітне поле, напрямленого руху атомів немає. Чому в такому разі на нього діє магнітна сила Ампера? |
| 3.33. |
На одиницю довжини прямого провідника зі струмом 0,2А в магнітному полі з індукцією 10 мТл діє сила Ампера 1 мН/м. Під яким кутом до напряму поля розташовано провідник? [30°] |
| 3.34. |
По стрижню довжиною 25 см і масою 0,5 кг, який лежить на горизонтальній поверхні у вертикальному магнітному полі, пропускають електричний струм, поступово збільшуючи його величину. Чому дорівнює індукція поля, якщо при коефіцієнті тертя 0,2 стрижень починає ковзати, коли струм досягає 50 А. [80 мТл] |
| 3.35. |
По прямокутній рамці площею 5 см2, що розташована паралельно до напряму магнітного поля з індукцією 10 мТл, протікає струм 1 А. Визначити обертовий момент, який діє на рамку. [5 мкН·м] |
| 3.36. |
Провідне кільце діаметром 20 см і опором 10 мОм, знаходиться в перпендикулярному до нього магнітному полі, індукція котрого змінюється зі швидкістю 100 мТл/с. Визначити силу струму в кільці. [≈ 0,3 А] |
| 3.37. |
В котушці індуктивності, що має 500 витків, магнітний потік за 0,5 c рівномірно змінюється від 7 мВб до 4 мВб. Визначити ЕРС, що виникає в котушці. [4 В] |
|
Визначити індуктивність котушки, в якій в при зміні струму на 2 А за 1 с індукується середня ЕРС 20 мВ. [2, 5 мГн] |
|
| 3.39. |
Знайти середню швидкість зміни власного магнітного потоку крізь поперечний переріз соленоїда з 2000 витків, якщо при відключенні від джерела струму в ньому індукується середня ЕРС 25 В. [12,5 мВб/с ] |
| 3.40. |
Круглий дротяний виток радіусом 10 см і опором 100 мОм знаходиться в перпендикулярному до його площини магнітному полі з індукцією 20 мТл. Який заряд пройде по витку при його розтяганні в лінію за діаметральні точки? [12,6 мКл] |
| Рівень Б | |
|
3.41. |
Дротяний коловий контур із струмом перекручують у формі "вісімки" й перегинають так, що утворюються два однакові складені круглі витки. Взявши до уваги, що індукція магнітного поля в центрі колового контуру є обернено пропорційна його радіусу, визначити її величину в центрі утворених витків, якщо у вихідному контурі вона складала В0. [4В0] |
| 3.42. |
Магнітне поле створюється трьома рівновіддаленими один від одного паралельними прямими провідниками зі струмом. Визначити його індукцію на осі симетрії струмів, якщо кожен провідник створює на ній поле з індукцією В. Розглянути випадки: а) один струм спрямований протилежно до інших; б) напрями всіх струмів однакові. [а) 2В; б) 0] |
| 3.43. |
Магнітне поле створюється довгим прямим провідником із струмом, який зігнуто під прямим кутом. Визначити, який модуль має та як напрямлений вектор індукції \({{\vec{B}}}\) в точці, що розташована на перпендикулярі до площини провідника над вершиною кута, якщо розпрямлений провідник створює в ній поле із заданою з індукцією В0. $\left[ {{B}_{0}}/\sqrt{2}\right]$, паралельно до бісектриси кута згину. |
|
Прискорений електричним полем електрон влітає в магнітне поле з індукцією 10 мТл і рухається далі по колу радіуса 1 мм. Яку прискорювальну напругу пройшов електрон? [9 В] |
|
|
3.45. |
Електрон влітає в область простору із взаємно перпендикулярними електричним (Е = 10 кВ/м) і магнітним (В = 10 мТл) полями й відтак рівномірно та прямолінійно рухається зі швидкістю v = 2·106 м/c. Визначити напрям його руху. [30° до напряму магнітного поля] |
| 3.46. |
Електрон, який із швидкістю 106 м/с влітає в зону взаємно паралельних електричного (Е = 100 В/м) і магнітного (В = 100 мкТл) полів перпендикулярно до їхнього напрямку. З яким прискоренням він буде рухатися далі? [2,5·1013 м/с2] |
| 3.47. |
Електрон, прискорений напругою 45 В, влітає в однорідне магнітне поле з індукцією 100 мкТл під кутом 30° до його напрямку. Визначити радіус і крок гвинтової траєкторії та період обертання електрона по ній. [1,1 м; 12,3 м; 3,6 мкс] |
|
Електрон, що пройшов прискорювальну напругу U = 4,5 кВ, потрапляє в однорідне магнітне поле і рухається в ньому по гвинтовій лінії з радіусом R = 8 см і кроком h = 30 см. Визначити індукцію магнітного поля B. [2,4 мТл] |
|
| 3.49. |
Дротяне кільце радіуса R зі струмом І знаходиться в однорідному магнітному полі з індукцією В, що напрямлене перпендикулярно до площини кільця. Визначити силу Ампера, що діє: а) на малу ділянку ηR (η <<1) і б) на все кільце. [а) 2πηRB; б) 0] |
|
По похилій площині з кутом нахилу 30°, яка знаходиться в перпендикулярному до неї однорідному магнітному полі, з певним прискорення зісковзує з тертям горизонтальний брусок довжиною 20 см і масою 100 г. Визначити індукцію поля, якщо при пропусканні по бруску струму 50 А він починає з таким самим прискоренням ковзати вгору. [0,2 Тл] |
|
| 3.51. |
Мідний (ρ = 8,9 г/см3) стрижень діаметром 5 мм горизонтально підвішено на двох нитках і вміщено в перпендикулярне до нього горизонтальне магнітне поле з індукцією 50 мТл. Якої величини струм слід пропустити по стрижню, аби він став невагомим? [35 А] |
| 3.52. |
Квадратну дротяну рамку зі стороною 10 см із увімкненим у неї конденсатором ємністю 100 мкФ розмістили в перпендикулярні до її площини однорідному магнітному полі. Визначити, який заряд накопичиться на конденсаторі при зміні індукції поля зі швидкістю [5 нКл] |
| 3.52. |
Короткозамкнену дротяну котушку опором 160 Ом, що складається з 1000 витків перерізом 40 см2, вмістили в спрямоване вздовж її осі однорідне магнітне поле. Яка кількість теплоти буде виділятися в котушці за одиницю часу при рівномірній зміні його індукції зі швидкістю 1 мТл/с? [0,1 мДж/с] |
| 3.53 |
Квадратну рамку зі стороною 4 см і опором 2 Ом вміщено в перпендикулярне до її площини магнітне поле з індукцією 10 мТл. Визначити заряд, який пройде по рамці при її повороті на 180 навколо осі, що лежить у її площині. [16 мкКл] |
| 3.54. |
Електричне коло опором300 Ом живиться від генератора постійного струму. Яка напруга подається на вхід кола, якщо на обертання ротора генератора витрачається потужність 50 Вт при втратах на тертя 4%? [120 В] |
|
Рівень В |
|
| 3.55. |
Заряджена частинка починає горизонтально рухатись із швидкістю 5·104 м/с у вертикальних магнітному та електричному полях із заданими характеристиками 125 мТл і 10 В/см, відповідно. Визначити, під яким кутом до горизонту рухатиметься частинка на момент, коли вперше опиниться над початковою точкою. [45°] |
|
Шайба маси 50 г і зарядом 25 мКл починає рухатися по гладкій горизонтальній поверхні у взаємно перпендикулярних горизонтальних електричному (Е = 12,5 В/см) і магнітному (В = 4 мТл) полях. Визначити, через який час шайба відірветься від поверхні. [8 с] |
|
|
По довгій похилій площині з кутом нахилу 30° до горизонту, що вміщена в паралельне до її ребра магнітне поле з індукцією 55 мТл, починає зісковзувати шайба із масою 25 г і зарядом 10 Кл. Якої максимальної швидкості вона набуде при коефіцієнт тертя з площиною 0,2. [15 см/с] |
|
| 3.58. |
При вміщенні атома водню в магнітне поле циклічна частота ω (кутова швидкість) його обертання навколо ядра змінилася на η =10–4 %. Вважаючи, що площина колової орбіти електрона є перпендикулярною до напрямку поля й має радіус r = 0,53 пм, визначити індукцією поля В.$\left[ 2\eta \sqrt{\frac{m}{4\pi {{\varepsilon }_{0}}{{r}^{3}}}}\approx 0,47 Тл\right]$ |
| 3.59. |
На провідник із струмом у формі половини кола, що вміщений в паралельне до його площини однорідне магнітне поле, діє сила Ампера 78,5 мН. Якою вона ста, коли провідник повернули на 90° навколо осі, що проходить через його кінці? [50 Н] |
| 3.60. |
Жорстке кільце діаметром 10 см із дроту перерізом 5 мм2 є розташовано перпендикулярно до магнітного поля з індукцією 1 Тл. Яка механічна напруга (сила натягу на одиницю площі перерізу дроту) виникне в кільці при пропусканні по ньому струму 5 А? [50 кПа] |
| 3.61. |
Довгий вертикальний П-подібний каркас із товстого дроту з ковзною провідною перетинкою масою 1 г і опором 2,5 мОм, яку утримують у спокої, вміщено в перпендикулярне до площини каркасу магнітне поле з індукцією 20 мТл. Якої максимальної швидкості набуде перетинка після вивільнення, якщо відстань між сторонами каркасу 50 см і тертя відсутнє? [25 см/с] |
| 3.62. |
На двох паралельних горизонтальних провідних шинах з відстанню між ними 20 см, які з одного кінця замкнено на резистор 100 мОм і вміщено у вертикальне магнітне поле з індукцією 0,5 Тл, лежить металева поперечка. Яку силу треба прикладати до неї, аби тягти зі швидкістю ? Тертя та опір шин і стержня не враховувати. [100 мН] |
| 3.63. |
На зігнуту під кутом α = 60° в горизонтальній площині й уміщену у вертикальне магнітне поле В = 1 мТл металеву шину впоперек поклали таку саму пряму шину-перемичку. Визначити силу струму в утвореному провідному контурі при переміщенні перемички вздовж бісектриси кута α зі швидкістю v = 30 см/с, якщо опір одиниці довжини шини складає r =1 мОм/м. (Підказка. Розглянути ЕРС, яка виникає в контурі при якомусь дуже малому переміщенні перемички). $\left[ I=\frac{Bv}{3r}=0,1A \right]$ |
| 3.64. |
На двох паралельних металевих стрижнях, які розташовані на відстані 10 см м один від одного в горизонтальній площині й уміщені у вертикальне магнітне поле з індукцією 0,1 Тл, лежить провідна поперечка маси 100 г. Визначити, до якої швидкості розженеться перетинка, якщо після підключення до кінців стрижнів джерела струму із внутрішнім опором 100 мОм вона починає ковзати з прискоренням 0,1 м/с2. Тертям та опором стрижнів і поперечки знехтувати. [10 м/с] |
| 3.65. |
Визначити ККД двигуна, якщо в момент підключення до джерела постійної напруги струм в обмотці його ротора складає 15 А, а в усталеному режимі — 9 А. [40%] |
|
3.66. |
Іграшковий електровоз, який живиться від батарейки з ЕРС 4,5 В, споживає робочий струм 200 мА. Яку потужність розвиває його двигун, якщо при повному гальмуванні ротора струм зростає до 300 мА? [300 мBт] |