ФІЗИКА. Вчимося розв'язувати задачі. "ЕЛЕКТРИКА І МАГНЕТИЗМ". Компенсаційний курс
Розділ ІІ. Постійний електричний струм
Закон Ома
Задача 2.11. Визначити відносну похибку ε виміру напруги на резисторі R = 10 Ом вольтметром із власним опором RV = 100 Ом.
Задача 2.12. Визначити додатковий опір RД, який треба підключити до вольтметра із власним опором RV = 10 кОм, аби розширити його діапазон вимірювань у n = 10 разів.
Задача 2.13. Визначити опір резистора (шунта) Rш, який слід приєднати до амперметра із власним опором RA = 0,6 Ом, аби розширити діапазон вимірювань у n = 10 разів.
Задача 2.14. Напруга на кінцях заданого ланцюжка (рис. 14) UАВ = 10 В, а опори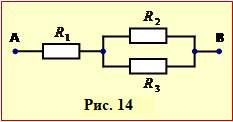 резисторів R1 = 3,5 Ом, R2 = 2 Ом, R3 = 6 Ом. Визначити струми I1, I2, I3 та напруги U1, U2, U3 на всіх резисторах.
резисторів R1 = 3,5 Ом, R2 = 2 Ом, R3 = 6 Ом. Визначити струми I1, I2, I3 та напруги U1, U2, U3 на всіх резисторах.
Задача 2.15. Резистор з опором R = 10 Ом і невідомий резистор Rx, що з’єднані між собою один раз послідовно, а інший паралельно, підключають до джерела із внутрішнім опором r = 2 Ом. Визначити опір Rx невідомого резистора, якщо в обох випадках струм у ньому однаковий.
Задача 2.16. Струм у підключеному до джерела резисторі R1 = 2 Ом складає I1 = 5 А, а напруга на підключеному натомість резисторі R2 = 120 Ом U2 = 12 В. Знайти струм короткого замикання джерела I0.
Задача 2.17. Два джерела з ЕРС і внутрішніми опорами ${{\E}_{1}}$ = 2 В, r1 = 0,4 Ом та ${{\E}_{2}}$ = 1,5 В, r2 = 0,6 Ом з’єднан0 однойменними полюсами. Визначити різницю потенціалів на клемах Δφ і силу струму в джерелах I.
Задача 2.18. Два ідеальні (без внутрішнього опору) джерела ${{\E}_{1}}$ = 4,5 В, ${{\E}_{2}}$= 2В і три резистори R1 = 1,5 Ом, R2 = 1 Ом, R = 4 Ом, є з'єднані, як показано на рис.18. Визначити величину і напрям струму в кожному резисторі.
${{\E}_{2}}$= 2В і три резистори R1 = 1,5 Ом, R2 = 1 Ом, R = 4 Ом, є з'єднані, як показано на рис.18. Визначити величину і напрям струму в кожному резисторі.
Задача 2.11
Визначити
відносну похибку ε виміру напруги на резисторі R = 10 Ом вольтметром із власним опором RV = 100 Ом.
|
Дано: R = 10 Ом RV = 100 Ом
|
|
ε - ?
|
Розв'язання
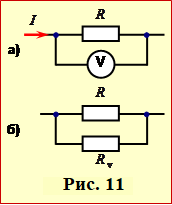
Вольтметр підключається до резистора паралельно і показує напругу на утвореному ланцюжку (рис. 11) опором (формула 2.16а)
|
${{R}_{0}}=\frac{{{R}_{V}}R}{{{R}_{V}}+R}$ |
(1) |
 Тож виміряна UV та істинна U напруги за законом Ома (2.10) дорівнюють UV = IR0 і U = IR, де І – струм у підвідних проводах, який уважатимемо незмінним. Отже, відносна похибка виміру
Тож виміряна UV та істинна U напруги за законом Ома (2.10) дорівнюють UV = IR0 і U = IR, де І – струм у підвідних проводах, який уважатимемо незмінним. Отже, відносна похибка виміру
$\varepsilon =\frac{U-{{U}_{V}}}{U}$ = $\frac{R-{{R}_{0}}}{R}$
і, з урахуванням виразу (1), складає
|
$\varepsilon =\frac{{{R}}}{{{R}_{V}}+R}$ ≈ 9 %. |
(2) |
З приводу отриманого результату слід зробити два зауваження.
1.Теоретично струми в проводах до і після підключення вольтметра мають відрізнятися через зміну опору даної ділянки кола. Але спричинена цим можлива зміна струму є настільки незначною, що не вартує уваги.
2. Як видно з виразу (2), для забезпечення достатньої точності вимірів вольтметр має мати доволі великий власний опір. До прикладу, при допустимій похибці ε ≤ 1% має бути RV ≥ 100R. Тому для прецизійних (надточних) вимірювань використовують інші, непрямі методи визначення напруги.
Задача 2.12
Визначити
додатковий опір RД, який треба підключити до вольтметра із власним опором RV = 10 кОм, аби розширити його діапазон вимірювань у n = 10 разів.
|
Дано: RV = 10 кОм
n = 10
|
|
RД - ?
|
Розв’язання
Кожен вольтметр може безпосередньо вимірювати лише напруги, котрі не перевищують певної величини Um, яка визначає його діапазон вимірювань (шкалу). Але шкалу вольтметра можна розширити, якщо безпосередньо подавати на нього не всю вимірювану напругу, а тільки її визначену частку. Для цього до вольтметра послідовно підключають додатковий опір ("добавку") – резистор із заданим опором RД (рис.12).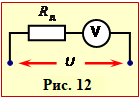
Необхідну величину RД легко розрахувати. Позаяк струм у складових ланцюжка вольтметр-добавка однаковий, то відповідно до закону Ома (2.10),
$\frac{U}{{{U}_{V}}}=\frac{{{R}_{}}+{{R}_{V}}}{{{R}_{V}}}$ $\Rightarrow $ ${{R}_{Д}}={{R}_{V}}\left( \frac{U}{{{U}_{V}}}-1 \right)$,
де U – подана напруга, і UV, RV – напруга на вольтметрі та його власний опір.
За умовою при UV = Um подана напруга U має дорівнювати nUm, отже
для розширення шкали вольтметра в n разів до нього треба послідовно підключити додатковий опір
RД = (n – 1)RV,
який, згідно з даними умови, дорівнює 90 кОм.
Задача 2.13
Визначити
опір резистора (шунта) Rш, який слід приєднати до амперметра із власним опором RA = 0,6 Ом, аби розширити діапазон вимірювань у n = 10 разів.
.
|
Дано: RA = 0,9 Ом
n = 10
|
|
Rш - ?
|
Розв’язання
За змістом і логікою розв'язування дана задача є аналогом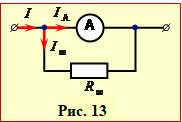 попередньої. А саме, для розширення діапазону вимірювань (шкали) до амперметра паралельно підключають "шунт" – резистор із заданим опором Rш (рис. 13),– за допомогою котрого від амперметра відгалужують надлишковий струм величиною
попередньої. А саме, для розширення діапазону вимірювань (шкали) до амперметра паралельно підключають "шунт" – резистор із заданим опором Rш (рис. 13),– за допомогою котрого від амперметра відгалужують надлишковий струм величиною
\(I_{ш}=I-I_{А}\),
де І – вимірюваний струм, ІА – струм, що проходить через амперметр. За умовою І = nІА, отже,
Іш = (n–1)ІА,
і, позаяк напруга на амперметрі та шунті однакова, відповідно до закону Ома (2.10),
для розширення шкали амперметра в n разів до нього треба паралельно підключити шунт опором
${{R}_{ш}}=\frac{{{R}_{A}}}{n-1}$.
За умовою n = 10, отже, відповідь
Rш = 0,1 Ом.
Задача 2.14
 Напруга на кінцях заданого ланцюжка (рис. 14) UАВ = 10 В, а опори резисторів R1 = 3,5 Ом, R2 = 2 Ом, R3 = 6 Ом.
Напруга на кінцях заданого ланцюжка (рис. 14) UАВ = 10 В, а опори резисторів R1 = 3,5 Ом, R2 = 2 Ом, R3 = 6 Ом.
Визначити
струми I1, I2, I3 та напруги U1, U2, U3 на всіх резисторах.
|
Дано: UAB = 10 В
R1 = 3,5 Ом
R2 = 2 Ом
R3 = 6 Ом
|
|
I1, I2, I3 - ?
U1, U2, U3 - ?
|
Розв’язання
Замінимо у початковій схемі резистори R2, R3 на один еквівалентний з опором R23 (формула (2.16а))
|
\(R_{23}=\frac{R_{2}R_{3}}{ R_{2}+R_{3}}=1,5\ {Ом}\) |
(1) |
отримаємо послідовне з’єднання резисторів R23 і R1 (рис.14-1) із загальним опором R0 = R23 + R1, напруга на якому дорівнює UAB. Отже, за законом Ома (2.10) загальний струм у ланцюжку, тож у резисторі R1, струм дорівнює
\(I_{0}=I_{1}=\frac{U}{R_{0}}=\frac{U}{R_{23}+R_{1}}=2\ {А}\),
і напруга
\(U_{1}=I_{0}R_{1}=7\ {В}\),
Відповідно, напруга на резисторах R2 і R3 дорівнює
|
\(U_{23}= U_{АВ}-U_{1}=3\ {В}\), |
(2) |
а струми становлять
|
|
\(I_{2}=\frac{U_{23}}{R_{2}}=1,5\ {А}\); \(I_{3}=\frac{U_{23}}{R_{3}}=0,5\ {А}\). |
|
Враховуючи співвідношення (2) і формулу (1) вирази струмів I2, I3 можна переписати, як
\(I_{2}=I_{0}\frac{R_{3}}{R_{2}+R_{3}}\);
\(I_{3}=I_{0}\frac{R_{2}}{R_{2}+R_{3}}\).
і сформулювати наступний алгоритм обчислення:
при паралельному з’єднанні двох резисторів струм в одному дорівнює загальному струмові, помноженому на опір іншого й поділеному на їхній сумарний опір.
”Інший” резистор називається ”стороннім опором”, а сформульований рецепт обчислення – ”правилом стороннього опору” і використовується в електротехніці при практичних розрахунках.
Задача 2.15
Резистор опором R = 10 Ом і невідомий резистор Rx, що з’єднані між собою один раз послідовно, а інший паралельно, підключають до джерела із внутрішнім опором r = 2 Ом.
Визначити
опір Rx невідомого резистора, якщо в обох випадках струм у ньому однаковий.
|
Дано: r = 2 Ом
R = 10 Ом
|
|
Rx - ?
|
Розв’язання
Якщо позначити загальний опір підключених до джерела резисторів при послідовному з'єднанні (рис.15а) як R1, і при паралельному (рис.15б) як R2, а сили струму як І1 й І2, то за законом Ома (2.13)
|
${{I}_{1}}=\frac{\E}{{{R}_{1}}+r}$; ${{I}_{2}}=\frac{\E}{{{R}_{2}}+r}$. |
(1) |
За умовою струм через резистор Rx у другому випадку є такий самий як і в першому, тобто І1. Отже за розглянутим у попередній задачі "правилом стороннього опору" можна записати:
|
${{I}_{1}}={{I}_{2}}\frac{R}{{{R}_{1}}}$ $\Rightarrow $ $\frac{{{I}_{2}}}{{{I}_{1}}}=\frac{{{R}_{1}}}{R}$ |
|
і, почленно поділивши вирази (1),
|
$\frac{{{R}_{1}}}{R}=\frac{{{R}_{1}}+r}{{{R}_{2}}+r}$. |
(2) |
Відтак, зробивши в цьому виразі підстановки
${{R}_{1}}=R+{{R}_{x}}$;
${{R}_{2}}=\frac{R{{R}_{x}}}{R+{{R}_{x}}}$.
й розв'язавши отримане рівняння, дістанемо наступну відповідь:
\(R_{x}=\frac{R^{2}}{r}=50\) Ом.
(Вказівка. При розв'язуванні рівняння варто ввести заміну Rх = ηR і шукати параметр η).
Задача 2.16
Струм у підключеному до джерела резисторі R1 = 2 Ом складає I1 = 5 А, а напруга на підключеному натомість резисторі R2 = 120 Ом U2 = 12 В.
Визначити
струм короткого замикання джерела I0.
|
Дано: R1 = 2 Ом
I1 = 5 А
R2 = 120 Ом
U2 = 12 В
|
|
I0 - ?
|
Розв’язання
Струмом короткого замикання джерела називається струм, який виникає при його "закорочуванні", тобто з'єднанні полюсів дротом із гранично малим опором R = 0. Отже, за законом Ома (2.13) маємо:
|
|
${{I}_{0}}=\frac{\E}{r}$ |
(1) |
де \(\E\) і r – ЕРС і внутрішній опір джерела.
Так само, відповідно до виразів закону Ома (2.13) і (2.7), можна скласти систему рівнянь
|
$\begin{align} & {{I}_{1}}=\frac{\E}{{{R}_{1}}+r} \\ & {{U}_{2}}=\frac{\E}{{{R}_{1}}+r}{{R}_{2}} \\ \end{align}$ |
(2) |
і знайти величини $\E$ та r, а відтак за формулою (1) – шуканий струм короткого замикання I0. Але, позаяк у рівняннях (2) опір джерела r є "зав'язаний" на опори R1, R2, визначення величин $\E$ та r порізно прямими підстановками потребує громіздких викладок. Проте струм I0 можна знайти одразу, застосовувати наступний штучний спосіб.
Перепишемо вираз (1) і рівняння (2) в "перевернутому" вигляді й, зробивши підстановку
\(\frac{r}{\E}=\frac{1}{{{I}_{0}}}\),
отримаємо:
$\begin{align} & \frac{1}{{{I}_{1}}}-\frac{1}{{{I}_{0}}}=\frac{{{R}_{1}}}{\E} \\ & \frac{1}{{{U}_{2}}}-\frac{1}{{{I}_{0}}{{R}_{2}}}=\frac{1}{\E} \\ \end{align} $.
Відтак, почленно помноживжи друге рівняння на R1 та прирівнявши праві частини, легко отримаємо наступну загальну відповідь
${{I}_{0}}=\frac{{{I}_{1}}{{U}_{2}}\left( {{R}_{2}}-{{R}_{1}} \right)}{\left( {{U}_{2}}-{{I}_{1}}{{R}_{1}} \right){{R}_{2}}}$
та числове значення
I0 = 29,5 А.
Задача 2.17
Два джерела з ЕРС і внутрішніми опорами ${{\E}_{1}}$=2 В, \(r_{1}= 0,4\) Ом та ${{\E}_{2}}$= 1,5 В, \(r_{2}=0,6\) Ом з’єднан0 однойменними полюсами.
Визначити
різницю потенціалів на клемах Δφ і силу струму в джерелах I.
|
Дано: ${{\E}_{1}}$ = 2В ${{\E}_{2}}$=1,5В r1 = 0,4 Ом r2 = 0,6 Ом |
|
Δφ-?, I -?
|
Розв’язання
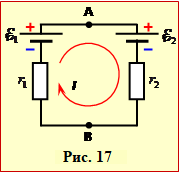 Джерела утворюють нерозгалужене коло (рис. 17) з двох ділянок А-В і В-А, з однаковим струмом I1 = I2 = І. Тож, увівши позначення φА – φВ = Δφ, за законом Ома (2.10) і виразом (2.7) маємо:
Джерела утворюють нерозгалужене коло (рис. 17) з двох ділянок А-В і В-А, з однаковим струмом I1 = I2 = І. Тож, увівши позначення φА – φВ = Δφ, за законом Ома (2.10) і виразом (2.7) маємо:
|
$\frac{-\Delta \varphi +{{\E}_{1}}}{{{r}_{1}}}=\frac{\Delta \varphi -{{\E}_{2}}}{{{r}_{2}}}\quad \Rightarrow \quad \Delta \varphi =\frac{{{\E}_{1}}{{r}_{2}}+{{\E}_{2}}{{r}_{1}}}{{{r}_{1}}+{{r}_{2}}}$ = 1,8 В. |
(1) |
|
І = 0,5 А. |
|
Отримані відповіді можна знайти й дещо інакше. А саме.
Указані джерела сполучені однойменними полюсами й утворюють батарею, до якої не підключено навантаження. Тож різниця потенціалів Δφ на полюсах А і В збігається з ЕРС і визначається формулами (2.20) і (2.21):
$\Delta \varphi =\frac{{{r}_{1}}{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}}\left( \frac{{{\E}_{1}}}{{{r}_{1}}}+\frac{{{\E}_{2}}}{{{r}_{2}}} \right)=\frac{{{\E}_{1}}{{r}_{2}}+{{\E}_{2}}{{r}_{1}}}{{{r}_{1}}+{{r}_{2}}}$ = 1,8 В.
Величину струму І теж можна визначити альтернативно, розглядаючи джерела як замкнене коло із загальною ЕРС $\E$ = ${{\E}_{1}}$– ${{\E}_{2}}$ і опором r = r1 + r2. У такому разі за законом Ома
$I=\frac{{{\E}_{1}}-{{\E}_{2}}}{{{r}_{1}}+{{r}_{2}}}$ = 0,5 А.
На завершення варто зауважити таке. Знайдений струм розряджає указані джерела, навіть коли вони не підключені до зовнішнього кола. Тому реально в батареї з'єднують тільки ідентичні елементи живлення, для яких І = 0.
Задача 2.18
Два ідеальні (без внутрішнього опору) джерела ${{\E}_{1}}$=4,5В, ${{\E}_{2}}$=2В і три резистори R1 = 1,5 Ом, R2 = 1 Ом, R = 4 Ом, є з'єднані, як показано на рис.18.
три резистори R1 = 1,5 Ом, R2 = 1 Ом, R = 4 Ом, є з'єднані, як показано на рис.18.
Визначити
величину і напрям струму в кожному резисторі.
|
Дано: ${{\E}_{1}}$ = 4,5 В, ${{\E}_{2}}$= 2ВR1 = 1,5 Ом R2 = 1 Ом R = 4 Ом |
|
I, I1, I2 - ?
|
Розв’язання
Напрямки шуканих струмів, які показано на рис. 18-1, фактично є очевидними. При заданій полярності джерел φА > φВ, отже, в резисторі R струм іде від А до В. А, з огляду на величини ЕРС, напрям струму в джерелах є такий, як у попередній задачі, бо через відсутність сторонніх сил у резисторі R він не впливає на напрямки струмів .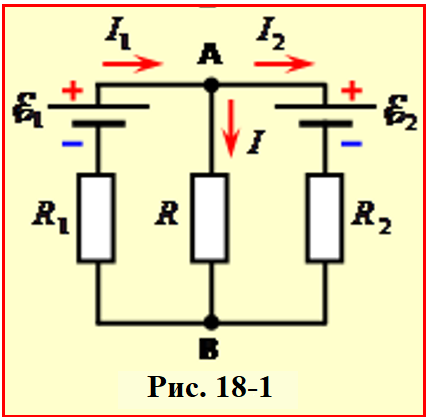
Що ж до величини струмів, то вона визначається законом Ома (2.12) для резистора R і (2.11) для R1 та R2 . Окрім того, за законом збереження заряду струм І1 в т. А розгалужується на І та І2 без зміни їхньої сумарної величини. Тож у відповідності із сказаним можна скласти наступну систему рівнянь:
|
${{I}_{1}}{{R}_{1}}={{\varphi }_{B}}-{{\varphi }_{A}}+{{\E}_{1}}$; ${{I}_{2}}{{R}_{2}}={{\varphi }_{A}}-{{\varphi }_{B}}-{{\E}_{2}}$; ${I}{R} ={{\varphi }_{A}}-{{\varphi }_{B}}$ ${{I}_{1}} =I+{{I}_{2}}$. |
|
${{I}_{1}}=\frac{{{\E}_{1}}\left( R+{{R}_{2}} \right)-{{\E}_{2}}R}{R{{R}_{1}}+{{R}_{1}}{{R}_{2}}+{{R}_{2}}R}$ = 1,26 A;
${{I}_{2}}=\frac{{{-\E}_{2}}\left( R+{{R}_{1}} \right)+{{\E}_{1}}R}{R{{R}_{1}}+{{R}_{1}}{{R}_{2}}+{{R}_{2}}R}$ = 0,61 A;
$I=\frac{{{\E}_{1}}{{R}_{2}}+{{\E}_{2}}{{R}_{1}}}{R{{R}_{1}}+{{R}_{1}}{{R}_{2}}+{{R}_{2}}R}$ = 0,65 A.