physics.zfftt.kpi.ua

Перш ніж розглядати наведені приклади варто уважно прочитати рекомендації по розв'язуванню задач цього типу.

Задача 2.4. Визначити довжину та діаметр намотаного на котушку мідного дроту масою 28 г і  опором 54,1 Ом. Густина міді D = 8900 кг/м³, питомий опір ρ = 17 нОм·м.

Задача 2.5. Плоский конденсатор ємністю C = 100 пФ заповнено  діелектриком із проникністю \(\varepsilon=2,1\) і питомим опором \(\rho\) = 10¹⁰ Ом·м. Визначити силу струму через конденсатор (струм ''витоку'') при напрузі U = 100 В.

Задача 2.6. Графітовий та залізний стрижні однакового перерізу з'єднують послідовно. Визначити, при якому відношенні довжин сумарний електричний опір стрижнів не залежатиме від температури. Термічний коефіцієнт опору графіту α₁ = –0,8·10^–3 K^–1; заліза α₂ = 6·10^–3 K^–1; відповідні питомі опори \(\rho_{1}= 40\) мкОм·м і \(\rho_{2}= 0,12\) мкОм·м.

Задача 2.7. При пропусканні через електричну лампу струму I₁ = 4 мА при початковій температурі t₁ = 20 °C напруга на вольфрамовій нитці розжарювання складає U₁ = 100 мВ. Визначити робочу температуру нитки t₂ при напрузі U₂ = 220 В і струмі I₂ = 0,7 A. Термічний коефіцієнт опору вольфраму α = 4,8·10^–3 K^–1.

Задача 2.8. Електричний опір послідовного з'єднання двох резисторів дорівнює R₀₁ = 8 Ом, а паралельного R₀₂ = 1,5 Ом. Визначити опір кожного резистора.

Задача 2.9. Потенціометр із повним опором R₀ включено в електричне коло в точках a і b, як  показано на рис.9. Показати графік залежності опору R всього потенціометра між точками a і b від опору r його правої частини.

Задача 2.10. Визначити опір R_ab між вершинами a-b сітки, виготовленої з дротин однакового опору R (рис.10).

Задача 2.4

Визначити

довжину та діаметр намотаного на котушку мідного дроту, якщо його маса 28 г і  електричний опір 54,1 Ом. Густина міді D = 8,9·10³ кг/м³, питомий опір ρ =17 нОм·м.

Розв’язання

Електричний опір і маса провідника відомими співвідношеннями пов'язані з розмірами (рис. 4) та відповідними характеристиками речовини:

Тож, почленно помноживши ці вирази, отримаємо довжину

$l=\sqrt{\frac{Rm}{\rho D}}$ = 100 м,

а поділивши – площу поперечного перерізу дроту:

$S=\sqrt{\frac{\rho m}{DR}}$ = 3,14·10^–2 мм²

і відтак – його діаметр:

$d=2\sqrt{\frac{S}{\pi }}$= 0,2 мм.

Задача 2.5

Плоский конденсатор ємністю C = 100 пФ заповнено  діелектриком із проникністю \(\varepsilon=2,1\) і питомим опором \(\rho\) = 10¹⁰ Ом·м. 

Визначити

силу струму через конденсатор (струм ''витоку'') при напрузі U = 100 В.

Розв’язання

Будь-який реальний діелектрик має хоча й дуже великий, але скінченний питомий опір. Тому через конденсатор, що перебуває під напругою, протікає певний "струм витоку". Тож у контексті задачі конденсатор є провідником із  заданим питомим опором \(\rho\) певним перерізом  S (площею обкладок), довжиною d (відстанню між ними, рис.5)

Задача 2.6.

Графітовий та залізний стрижні однакового перерізу з'єднують послідовно.

Визначити,

при якому відношенні довжин сумарний електричний опір стрижнів не залежатиме від температури. Термічний коефіцієнт опору графіту α₁ = –0,8·10^–3 K^–1, заліза α₂ = 6·10^–3 K^–1; відповідні питомі опори \(\rho_{1}= 40\) мкОм·м і \(\rho_{2}= 0,12\) мкОм·м.

Розв’язання

Температурна залежність опору обох стрижнів визначається однією формулою (2.9а). Але, позаяк α₁ і α₂ мають різний знак, опори стрижнів змінюються в протилежному напрямку: якщо в одному опір зростає, то в іншому зменшується і навпаки. Через це за відповідних умов у з’єднаних стрижнях вказані зміни можуть компенсуватись.

При послідовному з'єднанні резисторів опори додаються (формула (2.15)), отже, згідно з виразом (2.9а),  загальний опір стрижнів R при довільній температурі t складає:

\(R=R_{1}+R_{2}=R_{01}(1+\alpha_{1}t)+R_{02}(1+\alpha_{2}t)\) =

=\((R_{01}+R_{02})+(R_{01}\alpha_{1}+R_{02}\alpha_{2})t\),

де R₀₁, R₀₂ – опори при t = 0 °C. Звідси випливає, що величина R не залежатиме від температури, якщо

\((R_{01}\alpha_{1}+R_{02}\alpha_{2})t=0\)      \(\Rightarrow\)      \(R_{01}\alpha_{1}=-R_{02}\alpha_{2}\)      \(\Rightarrow\)      \(\frac{R_{01}}{R_{02}}=-\frac{\alpha_{2}}{\alpha_{1}}\).

З отриманого співвідношення, взявши до уваги однаковість перерізів стрижнів і формулу (2.8), знайдемо відповідь: 

\(\frac{l_{2}}{l_{1}} =  –\frac{\rho_{1}\alpha_{1}}{\rho_{2}\alpha_{2}}\) ≈ 44.

Варто зауважити, що такий принцип іноді використовують для нівелювання температурної залежності параметрів прецизійних електровимірювальних приладів.

 Задача 2.7

При пропусканні через електричну лампу струму I₁ = 4 мА при робочій температурі t₁ = 20 °C напруга на вольфрамовій нитці розжарювання складає U₁ = 100 мВ.

Визначити

робочу температуру нитки t₂ при напрузі U₂ = 220 В і струмі I₂ = 0,7 A. Термічний коефіцієнт опору вольфраму α = 4,8·10^–3 K^-1.

Розв’язання

За законом Ома (2.10) указані в умові струми та напруги по суті задають  значення R₁ і R₂ опору нитки розжарювання лампи, відповідно, при початковій t₁ і шуканій робочій температурі t₂:

R₁ = 25 Ом;  R₁ = 314,3 Ом.

Отже, згідно з виразом (2.9а), можна записати

$\frac{{{R}_{2}}}{{{R}_{1}}}=\frac{1+\alpha {{t}_{2}}}{1+\alpha {{t}_{1}}}$

і після простих перетворень отримати відповідь задачі:

Наведений розв'язок ілюструє метод вимірювання температури, що зветься "термометром опору" й дозволяє вимірювати високі та низькі температури в  діапазонах, які є недоступні для традиційних рідинних термометрів. При цьому для визначення температури якогось об'єкта із ним приводять у контакт і вимірюють опір R датчика – резистора із відомими значеннями R₀ і α. У такому разі за виразом (1) вимірювана температура дорівнює

де n = (R/R₀)_.

Задача 2.8. Електричний опір послідовного з'єднання двох резисторів дорівнює R₀₁ = 8 Ом, а паралельного R₀₂ = 1,5 Ом.

Визначити

опір кожного резистора.

Розв’язання

Якщо позначити опір одного з резисторів як R, то при послідовному з'єднанні (формула 2.15) опір іншого складе R₀₁– R. Отже, для паралельного з"єднання  (формула (2.1а)) маємо:

$\frac{R\left( {{R}_{01}}-R \right)}{{{R}_{01}}}={{R}_{02}}$   $\Rightarrow $   ${{R}^{2}}-{{R}_{01}}R+{{R}_{01}}{{R}_{02}}=0$

або в числах

${{R}^{2}}-8R+12=0$.

Корені цього рівняння дорівнюють

R₁ = 6 Ом;     R₂ = 2 Ом

і є відповідями задачі.

Задача 2.9

Потенціометр із повним опором R₀ включено в електричне коло в точках a і b, як  показано на рис.9.

Показати

графік залежності опору R всього потенціометра між точками a і b від опору r його правої частини.

Розв’язання

Потенціометр являє собою резистор, споряджений ковзним контактом а (повзунком), що залежно від способу включення дозволяє регулювати або струм, або напругу на інших ділянках кола.

Як зрозуміло з рис. 9 і 9-1 а-в, повзунок ділить опір потенціометра на дві паралельно з'єднані частини з опорами r і (R₀ – r). Отже, за формулою (2.16б) загальний опір між точками а і b в залежності від r складає

$R\left( r \right)=\frac{r\left( {{R}_{0}}-r \right)}{{{R}_{0}}}$. 

На графіку ця залежність зображується параболою з максимумом R_m = (R₀/4), як показано на рис.9-1 г

З приводу отриманого результату слід зауважити таке. Графік R(r) наочно показує, що після проходження повзунка через середнє положення величина R у зворотньому порядку набуває всіх попередніх значень. Тому розглянуте включення потенціометра в коло реально не має сенсу і на практиці не використовується. 

 Задача 2.10

Визначити

опір R_ab між вершинами a-b сітки, виготовленої з дротин однакового опору R (рис.10).  

 Дано:

Розв’язання

Сітка являє собою з'єднання 12 однакових резисторів R  (рис. 10-1а), котре не є ані паралельним, ані послідовним, отже, знайти відповідь безпосередньо за формулами (2.15), або (2.16) неможливо. Але задачу спрощує симетрія електричної схеми сітки, через що струми в симетричних гілках і потенціали симетричних вузлів збігаються. Тож не  важко збагнути, що з'єднання, або роз'єднання гілок у таких точках не вплине на розподіл струмів і потенціалів, тому при розрахунках сітку можна замінити більш простою еквівалентною схемою. Далі розглянуто дві такі можливості.

1. Якщо попарно з'єднати всі симетричні відносно діагоналі a-b вузли (рис. 10-1б), а потім за формулами (2.15а) та (2.16а) поступово ''згорнути'' отриману схему, як показано на рис.10-1в-д, то врешті дістанемо одну еквівалентну гілку (рис. 10е) і наступну відповідь:

R₀ = 1,5R.

2. Розірвавши схему в т. f, отримаємо вихідну еквівалентну схему рис. 10-2а і чинячи, як раніше (рис. 10-2 б-в), дістанемо ту саму відповідь.

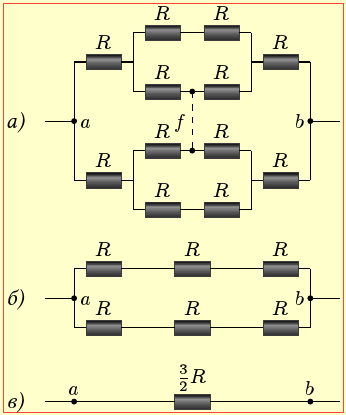
На завершення зауважимо, що розглянутий ланцюг є симетричним лише в електричному сенсі й реально зовсім не має складатися з геометрично упорядкованих однакових дротяних квадратиків.