ФІЗИКА. Вчимося розв'язувати задачі. "ЕЛЕКТРИКА І МАГНЕТИЗМ". Компенсаційний курс
Розділ ІІ. Постійний електричний струм
Характеристики електричного струму
|
При аналізі характеристик електричного струму носії розглядаються як частинки ідеального газу й використовуються відповідні співвідношення з молекулярно-кінетичної теорії. |
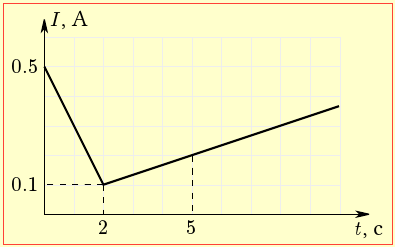
Задача 2.1. Сила електричного струму I у провіднику змінюється з часом t, як показано на графіку I(t). Визначити заряд q, який проходить провідником за перші 5 с.
Задача 2.2. За борівською моделлю атома електрон в атомі Гідрогену рухається навколо ядра по коловій орбіті радіуса R = 53 пм. Заряд електрона e = 1,6·10–19 Кл, маса m = 9,1·10–31 кг. Визначити силу еквівалентного струму I, що створюється цим рухом.
Задача 2.3. Густина струму в мідній дротині складає j = 1 А/мм2. Оцінити шлях S, який проходить кожен носій струму за час переміщення уздовж дротини на відстань l = 5 мм при температурі 20°С, прийнявши їхню концентрацію на рівні концентрації атомів.
Задача 2.1
Сила електричного струму I у провіднику змінюється з часом t, як показано на графіку. рис. 1.
Визначити
заряд q, який проходить провідником за перші 5 с.
|
Дано: I(t)
t1 = 0
t2 = 5 c
|
|
q - ?
I0 - ?
|
Розв’язання
При зміні сили струму з часом порція заряду \(\Delta{q_{k}}\), що в якийсь момент tk проходить провідником за малий проміжок часу \(\Delta{t_{k}}\), наближено складає
\(\Delta{q}_{k}\approx{I}(t_{k})\cdot\Delta{t}_{k}\)
і чисельно дорівнює площі відповідної вузької смужки на графіку I(t) шириною Δtk, рис. 1. Відповідно, заряд за весь заданий час наближено визначається сумарною площі таких смужок:
$q\approx \sum\limits_{k}{{{I}_{k}}\Delta {{t}_{k}}}$.
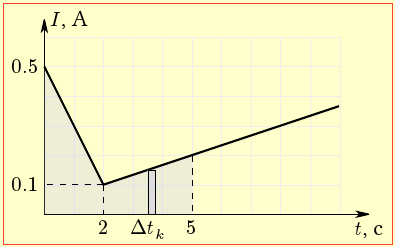
Зрозуміло, що при при зменшенні інтервалів \(\Delta{t_{k}}\) похибка розрахунку зменшується, тож точна величина q чисельно дорівнює площі виділеної ділянки графіка I(t), котра, як видно з рис. 1, утворює з осями координат дві стичні трапеції. Тож, обчисливши їхню сумарну площу за даними умови, дістанемо таку відповідь:
\(q=1,05\) (Кл).
Задача 2.2
За борівською моделлю атома електрон в атомі Гідрогену рухається навколо ядра по коловій орбіті радіуса R = 53 пм (рис. 2). Заряд електрона e = 1,6·10–19 Кл, маса m = 9,1·10–31 кг.
Визначити
силу еквівалентного струму I, що створюється цим рухом.
|
Дано: R = 53 пм = 53·10–12 м
e = 1,6·10–19 Кл
m = 9,1·10–31 кг
|
|
I - ?
|
Розв’язання
 Згідно із завданням, йдеться про величину заряду q, який за одиницю часу переноситься електроном крізь розташовану на його шляху уявну площинку при обертанні навколо ядра. Отже,
Згідно із завданням, йдеться про величину заряду q, який за одиницю часу переноситься електроном крізь розташовану на його шляху уявну площинку при обертанні навколо ядра. Отже,
| I = еn, |
(1) |
де n – частота обертання, тобто кількість обертів електрона по орбіті за 1 с.
Величину n не важко знайти, позаяк вона визначається доцентровим прискоренням ([І], ф-ла (1.28)) електрона, котре дорівнює відношенню сили його притягання до ядра (формула (1.3)) та масою. Тож
| 4π2n2R = $\frac{k{{e}^{2}}}{m{{R}^{2}}}$ $\Rightarrow $ $n=\frac{{{e}}}{2\pi R}\sqrt{\frac{k}{mR}}$. |
|
Відтак за виразом (1) знаходимо відповідь:
$I=\frac{{{e}^{2}}}{2\pi R}\sqrt{\frac{k}{mR}}$,
де k = (1/4πε0) = 9·109 м/Ф.
Обчислення дають:
І = 1,05·10–3 А ≈ 1 мА.
Задача 2.3.
Густина струму в мідній дротині складає j = 1 А/мм2.
Оцінити
шлях S, який проходить кожен носій струму за час переміщення уздовж дротини на відстань l = 5 мм при температурі 20°С, прийнявши їхню концентрацію на рівні концентрації атомів.
|
Дано: j = 1 А/мм2 = 106 А/м2
l = 5 мм = 5·10–3 м
t = 20°С
|
|
S - ?
|
Розв’язання
Упорядкований рух носіїв струму в металах, якими є вільні електрони, відбувається на тлі їхнього хаотичного теплового руху і в певному сенсі нагадує повільне зміщення (дрейф) рою комах під дією легкого вітерцю. Тому швидкість упорядкованого руху носіїв, яку називають дрейфовою швидкістю, є характеристикою не окремих носіїв, а всієї їхньої сукупності. Що ж до поодиноких носіїв, то через хаотичність теплового руху пройдений кожним із них шлях S набагато перевищує зміщення l уздовж провідника і складає
S = vt,
де v – середня швидкість теплового руху носіїв, і t = (l/u) – час їхнього переміщення (дрейфу) вздовж провідника на відстань l із дрейфовою швидкістю u. Отже шуканий шлях
|
\(S=\frac{v}{u}l\). |
(1) |
Дрейфову швидкість u можна визначити з формули (2.4) як
|
\(u=\frac{j}{en}\) |
(2) |
через задані густину струму j і відомий заряд e та концентрацію носіїв n = (N/V), що визначається їхньою кількістю в якомусь виділеному об'ємі провідника.
Величину n можна визначити з основних положень молекулярно-кінетичної теорії ([II], розділ І, п. 1.1). Дійсно, за умовою кількість носіїв у провіднику дорівнює кількості атомів N, отож складає
N = νNА,
де ν (моль) – кількість речовини у провіднику, NА – стала Авогадро (кількість атомів в одному молі). А об'єм
$V=\frac{m}{\rho }=\frac{\nu M}{\rho }$,
де ρ – густина, а m і M – маса виділеної частини провідника та молярна маса його речовини. Отже, для концентрації атомів, тож і носіїв струму, маємо
| $n=\frac{\rho {{N}_{A}}}{M}$. |
(3) |
Відтак за формулою (2) визначаємо дрейфову швидкість u:
|
|
$u=\frac{jM}{e\rho {{N}_{A}}}$, |
(4) |
де e = 1,6·10–19 Кл, NА = 6,02·1023 моль-1, густина міді ρ =(m/V) = 8,9·103 кг/м3, молярна маса M = 64·103 кг/моль. Обчислення дають
u ≈ 10–4 м/с = 0,1 мм/с.
Швидкість теплового руху носіїв (електронів) оцінимо за формулою середньоквадратичної швидкості частинок ідеального газу ([ІІ], ф-ла (1.9)):
\(v\approx\sqrt{\frac{3kT}{m}}\),
де k = 1,38·10-23 Дж/К – стала Больцмана, m = 9,1·10-31 кг – маса електрона, T = 293 К (20 °С). Тож
v ≈ 105 м/с.
Відтак, за отриманими значеннями v i u з формули (1) знайдемо наступну оцінку шляху, який проходить окремий носій за час дрейфу уздовж провідника на відстань l = 5 мм:
S ≈ 5000 км.
Отже, цей вражаючий результат свідчить, що спрощене уявлення про рух носіїв струму вздовж провідника зі струмом є вельми умовним.