physics.zfftt.kpi.ua

У механізмах і машинах окрім тіл, які обертаються навколо нерухомої осі чи здійснюють плоскі рухи (колеса, маховики, шатуни), використовують і так звані гіроскопи – масивні симетричні обертові тіла, осі обертання яких не є жорстко закріпленими і можуть змінювати напрям під час руху. Строга теорія гіроскопа є досить складною, тому обмежимося лише спрощеним розглядом окремих властивостей гіроскопів.

Зв’язок між векторами \( \vec{L} \)  і \( \vec{\omega} \). Визначимо вектор моменту імпульсу \(\vec{L}\) симетричного однорідного тіла, яке обертається зі сталою кутовою швидкістю \(\vec{\omega}\) навколо закріпленої осі, що збігається з його віссю симетрії. Для цього розглянемо сумарний момент імпульсу \({\Delta\vec{L}_i}\) будь-якої пари однакових симетричних частинок тіла масами Δm_i, які мають швидкості  \({\vec{v}_i}\) та  \({\vec{v}_i{'}}={-\vec{v}_i}\) (рис 7.8):

\( \Delta \vec{L_{i}}=\left[ {{{\vec{r}}}_{i}},\Delta {{m}_{i}}{{{\vec{v}}}_{i}} \right]+\left[ {{{\vec{r}}}_{i}}^{\prime },\Delta {{m}_{i}}{{{{\vec{v}}'}}_{i}} \right] \) = \( \left[ {{{\vec{r}}}_{i}},\Delta {{m}_{i}}{{{\vec{v}}}_{i}} \right]-\left[ {{{\vec{r}}}_{i}}^{\prime },\Delta {{m}_{i}}{{{\vec{v}}}_{i}} \right] \) = \( \left[ \left( {{{\vec{r}}}_{i}}-{{{\vec{r}}}_{i}}^{\prime } \right),\Delta m\vec{v} \right]=\left[ {{{\vec{r}}}_{i{i}'}},\Delta m\vec{v} \right] \).

Оскільки вектор \(\vec{r}_{i}{'}=\left(\vec{r}_i-\vec{r}_i{'}\right) \) лежить на діаметрі кола, по якому рухаються частинки (див. рис. 7.9а), вектор їхнього сумарного моменту імпульсу  \(\Delta {{\vec{L}}_{i}}\)    за напрямом збігається з вектором кутової швидкості тіла \(\vec{\omega}\). Із подібних парних елементів складається все симетричне тіло, тому його повний момент імпульсу а \(\vec{L}\) напрямлений так само. В такому разі, враховуючи (7.16), маємо:

Отже, вектор моменту імпульсу симетричного тіла, що обертається навколо закріпленої осі симетрії, дорівнює добутку його моменту інерції відносно цієї осі на вектор кутової швидкості і не залежить від положення точки відліку на осі обертання. Якщо ж вісь обертання не збігається з віссю симетрії тіла, то вектор  \( \vec{L} \) складає якийсь кут α з вектором \( \vec{\omega } \) (рис. 7.9б). Тому, обертаючись разом із тілом, вектор \( \vec{L}\) описує конус, а його кінець рухається по колу в перпендикулярній до осі обертання площині. Отже, вектор моменту імпульсу тіла  за будь-який елементарний проміжок часу dt набуває приросту, вектор якого \( \mathrm{d}\vec{L}\) є дотичним до цього кола і перпендикулярним до осі обертання. У відповідності до рівнянням (7.6), це означає, що на тіло діє певний момент сил однакового з \( \mathrm{d}\vec{L} \) напрямку. Він створюється поперечними силами реакції опор (підшипників) \( {\vec{F}}'\) і \({\vec{F}}''\), які виникають через асиметричність розподілу маси тіла відносно осі обертання. Відповідно, з боку осі на підшипники діють такі самі сили протилежного напрямку, котрі можуть призвести до швидкого зносу чи навіть руйнування підшипників і спричинюють шкідливі вібрації пристрою, в якому закріплені підшипники. Тому при виготовленні обертових деталей та вузлів механізмів і машин забезпечують їхнє балансування, тобто максимально симетричний розподіл маси відносно осі обертання.

Вільний зрівноважений гіроскоп.

Як говорилося, гіроскопом називається масивне симетричне тіло (маховик), що може обертатися з великою швидкістю навколо осі симетрії. Зазвичай гіроскоп уміщують у так званий кардановий підвіс, який являє собою систему з трьох концентричних рухомих кілець[9] (рис. 7.10а). Маховик і кільця можуть вільно обертатися навколо взаємно перпендикулярних осей АА', ВВ' і DD' (рис.7.10б), що забезпечує можливість орієнтації осі гіроскопа АА' у будь-якому напрямі. Тому гіроскоп у кардановому підвісі називається вільним гіроскопом. Зазвичай одна з точок осі гіроскопа є закріпленою, і її називають точкою опори гіроскопа. У показаному на рис. 7.10 гіроскопі точкою опори є спільний центр кілець. Нарешті, якщо точка опори збігається з центром мас маховика, то гіроскоп називають зрівноваженим.

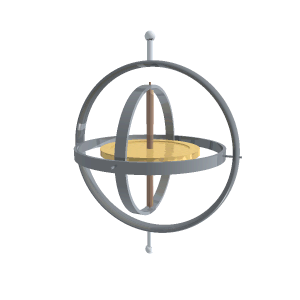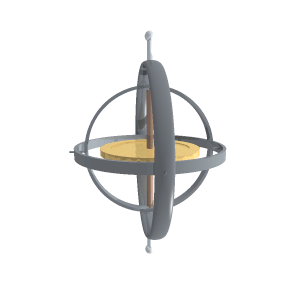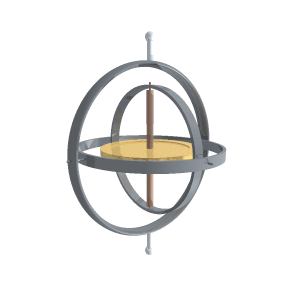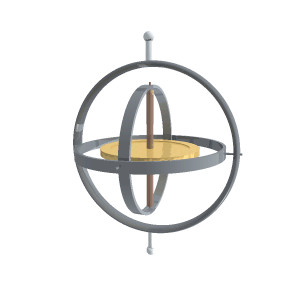Очевидно, що сума моментів усіх зовнішніх сил, які діють на вільний зрівноважений гіроскоп, дорівнює нулю. Тому, згідно із законом збереження моменту імпульсу, напрям осі гіроскопа буде лишатися незмінним навіть, якщо його каркас буде рухатися довільним чином. На цьому базується робота гірокомпаса – приладу, який дозволяє визначати напрям у просторі, не використовуючи магнітне поле Землі.

З властивостями гіроскопа можна познайомитися, переглянувши фільми за наведеними нижче посиланнями

Гіроскопічний ефект.

Якщо на гіроскоп почне діяти зовнішній момент сил, то його момент імпульсу буде змінюватись у відповідності до рівняння моментів (7.7):

При цьому вісь гіроскопа поводиться досить несподівано. Якщо у зображеному на рис. 7.11а вільному зрівноваженому гіроскопі (кардановий підвіс не показано) спробувати повернути вісь гіроскопа АА' за годинниковою стрілкою навколо перпендикулярної до неї горизонтальної осі ВВ', приклавши дві антипаралельні сили (пару сил) \({{\vec{F}}_{1}}\) – \({{\vec{F}}_{2}}\), то всупереч очікуванням вісь гіроскопа повернеться не у вертикальній площині навколо горизонтальної осі ВВ', а в горизонтальній площині навколо вертикальної осі DD'. Така поведінка осі гіроскопа під дією зовнішніх сил називається гіроскопічним ефектом. Хоча цей ефект важко сприймається, він прямо випливає з рівняння моментів. Справді, прикладена пара сил створює відносно точки опори гіроскопа О момент \(\vec{M}\), який за правилом правого гвинта напрямлений уздовж горизонтальної осі ВВ' (рис. 7.11а). Тож за з рівнянням (7.29) такий самий напрям має і вектор приросту моменту імпульсу гіроскопа \(d\vec{L}\). А це означає, що вектор \(\vec{M}\), а з ним і вісь гіроскопа АА' , повертається в горизонтальній площині навколо вертикальної осі _{DD ′}.

          Уявімо тепер тепер, що кільце, в діаметральних точках якого А, А'  зафіксована в підшипниках вісь гіроскопа, розташоване горизонтально і рівномірно обертається в підшипниках навколо вертикальної осі DD ′ (рис 7.11б). Тоді разом із кільцем у горизонтальній площині обертається і вісь гіроскопа АА′  та вектор його моменту імпульсу \(d\vec{L}\). Позаяк він залишається в горизонтальній площині, вектор його приросту \(d\vec{L}\)  теж обертається в горизонтальній площині і є перпендикулярним до  \(\vec{L}\), тобто до осі гіроскопа. Згідно з (7.29), це означає, що при вимушеному обертанні осі гіроскопа на нього діє якийсь напрямлений горизонтально момент сил . Цей момент створюється вертикальними силами реакції , в підшипниках осі гіроскопа (рис. 7.11б). У свою чергу такі самі протилежно напрямлені сили і діють з боку осі на підшипники. Ці сили називають гіроскопічними силами, а створюваний ними момент – гіроскопічним моментом. Значні гіроскопічні сили виникають, наприклад, у підшипниках масивних роторів турбін кораблів при різких змінах курсу та у штормову погоду, або в підшипниках карданних валів автомобілів на крутих віражах, що може призвести до руйнування підшипників.

          Але гіроскопічний ефект знаходить і корисні застосування зумовлені тим, що гіроскоп чинить спротив зміні напрямку осі обертання. Приміром, масивні гіроскопи використовують для стабілізації положення  корабля, або вагонів монорейкової залізниці. Прояви гіроскопічного ефекту спостерігаються й при їзді на велосипеді чи мотоциклі, позаяк колеса швидко обертаються і “працюють” як гіроскопи. Це не дає байкеру падати при русі по прямій. При поворотах він також використовує гіроскопічний ефект. Відхиляючись при повороті від вертикалі, велосипедист повертає вісь переднього (кермового) колеса у вертикальній площині навколо напрямку руху, внаслідок чого виникає гіроскопічний момент, який повертає вісь колеса в горизонтальній площині, спонукаючи велосипед повертати в бік нахилу велосипедиста.

Прецесія гироскопа

      Ще одним проявом гіроскопічного ефекту є так званий прецесійний рух осі гіроскопа, або просто прецесія. Розглянемо це явище на прикладі відомої дитячої іграшки дзиґи – симетричного тіла, яке може швидко обертатись навколо власної осі на горизонтальній опорі як незрівноважений гіроскоп. Поставлена вертикально нерухома дзиґа неодмінно завалюється під дією сили тяжіння. Але розкручена  дзиґа  не падає навіть якщо відхилена – її вісь описує конус навколо вертикалі (рис. 7.12).  Такий рух називається прецесією осі.
     Поведінка осі дзиґи принципово не відрізняється від поведінки осі зрівноваженого гіроскопа і повністю пояснюється рівнянням моментів . Справді, сила тяжіння  \(m\vec{g}\)  , яка прикладена в центрі мас дзиґи,  створює зовнішній момент  \(\vec{M}\)  відносно точки опори О. Вектор \(\vec{M}\), тож  і вектор приросту моменту імпульсу  \(d\vec{L}\) , весь час  є перпендикулярними до вертикальної площини, в якій лежить вісь дзиґи та збіжний із нею за напрямом вектор \(d\vec{L}\). Тому вектор моменту імпульсу та вісь дзиґи під дією сили тяжіння не наближаються до площини точки закріплення, а прецесують – описують конуси навколо вертикалі ОZ із незмінним кутом розкриття. (Насправді через неодмінну наявність тертя в точці О та опору повітря обертання дзиґи буде поступово уповільнюватись, а кут α – зростати, і згодом дзиґа таки впаде).

     Знайдемо  кутову швидкість (частоту) прецесії Ω, скориставшись рис. 7.12 (початок вектора  \(\vec{L}\) знаходиться в т. О).  За час dt  кінець вектора  \(\vec{L}\)  рухається навколо осі ОZ по колу радіуса Lsinα  і за час dt повертається на кут dφ = dL/Lsinα . А за рівнянням моментів dL = Mdt . Звідси для кутової швидкості прецесії

 Ω =  dφ/dt  виходить:

Модуль моменту сили тяжіння відносно точки О дорівнює добутку її величини на відстань від центра мас дзиґи до осі OZ (плече), отже, у виразі (7.30) M = mgbsinα, де b – відстань від точки опори О до центра мас дзиґи С. Урахувавши також, що модуль моменту імпульсу \({L=I\omega}\), де ω – кутова швидкість обертання дзиґи навколо власної осі, отримаємо вираз кутової швидкості прецесії дзиґи

Варто зауважити, що завдяки прецесії кожна точка гіроскопа, крім обертання навколо власної осі із  кутовою швидкістю ω,  рухається ще і з кутовою швидкістю прецесії Ω навколо осі, що проходить через точку опори. Тому використаний при виведенні формули (7.31) вираз є наближеним. Але при великій частоті обертання  Ω << ω, і похибка є неістотною.

Зрозуміло, що вираз (7.30) чинний не лише для дзиґи, на яку діє момент сил тяжіння, а й для будь-якого незрівноваженого гіроскопа, що перебуває під дією зовнішнього моменту сил \(\vec{M}\). Тому доцільно співвідношення (7.30) записати  векторно в загальному  вигляді. Урахувавши напрямки векторів \(\vec{L}\), \(\vec{M}\) і \(\vec{\Omega}\), отримаємо:

Із цього виразу випливає цікава особливість прецесійного обертання осі гіроскопа: зовнішній момент сил визначає не кутове прискорення, як для "звичайного" тіла, а саму кутову швидкість прецесії. Отже, щойно зникає зовнішній момент, одразу припиняється й прецесія. Тому таку прецесію називають вимушеною.