physics.zfftt.kpi.ua

 

Увага. Тут і далі по замовчуванню прийнято наступні умови:

– світлові пучки  є параксіальні, тобто тонкі й не розбіжні;

– показники заломлення води й скла, відповідно, дорівнюють 1,33 і 1,5 .

Задача 2.1. Визначити кут відхилення \(\vartheta\) променя двогранним плоским дзеркалом із кутом між гранями \(\varphi\) при відбиванні в перпендикулярній до ребра площині.

Задача 2.2. Визначити, під яким кутом падає світло на межу поділу двох середовищ із відношенням показників заломлення k = 1,5, якщо відбитий та заломлений промені є взаємно перпендикулярні.

Задача 2.3. Спостерігач розглядає  порожню непрозору кубічну посудину з кулькою на дні так, що повністю бачить стінку посудини, але не бачить дна (див. рис. 3 в розв'язку). Визначити, до якого найменшого рівня h слід наповнити посудину водою, аби спостерігач  побачив кульку, якщо вона знаходиться на відстані S = 10 см від видимого краю дна.

Задача 2.4. На поверхні дотику двох пластин з показниками заломлення n₁ = 1,35 i n₂ = 1,95 та товщиною по h = 2 см зафарбовано круг радіусом r = h. Визначити радіус тіні R, яку відкидатиме круг на поверхню іншої пластини, якщо над його центром розмістити точкове джерело світла S на: А) першій пластині; В) другій пластині.

Задача 2.5. Промінь світла під кутом \(\alpha=60^{\circ}\) падає  з повітря  на скляну плоскопаралельну пластину товщиною d = 3 см. Визначити зміщення x променя внаслідок проходження пластини.

Задача 2.6. Пучок променів падає  на аркуш паперу під кутом \(\alpha=60^{\circ}\). Визначити, на яку відстань  S зміститься світна цятка на папері, якщо на нього покласти скляну пластину товщиною d = 5 см.

Задача 2.7. Рибалці в човні, котрий прямо під собою розглядає камінець на дні ставка, здається, що він знаходиться на глибині h = 3 м. Визначити справжню глибину ставка H.

Задача 2.8. Промінь, який падає на трикутну призму під кутом \(\alpha=30^{\circ}\) і виходить під кутом  \(\beta=60^{\circ}\), відхиляється на кут \(\delta=45^{\circ}\). Визначити заломний кут призми \(\varphi\).

Задача 2.9. Промінь світла під малим кутом падає на бічну грань скляної призми із заломним кутом \(\varphi=0,1\) рад. Визначити кут відхилення \(\delta\) променя призмою.

Задача 2.10. Промінь світла падає на бічну грань скляної призми із заломним кутом  \(\varphi=60^{\circ}\) і непрозорою основою. Визначити мінімальне значення кута падіння \(\alpha_{m}\), при якому світло проходитиме крізь призму.

 

Задача 2.1

Визначити

кут відхилення \(\vartheta\) променя двогранним плоским дзеркалом із кутом між гранями \(\varphi\) при відбиванні в перпендикулярній до ребра площині.

Дано: \(\varphi\)

\(\vartheta\) - ?

Розв’язання

На рис. 1 з урахуванням закону відбивання (2.2) показано хід променя, що падає й відбивається на першій грані дзеркала під якимось кутом \(\alpha_{1}\), а на другій – під відповідним кутом \(\alpha_{2}\), та шуканий кут відхилення \(\vartheta\), тобто кут між напрямами променя, що падає на першу грань дзеркала, та того, що відбивається від  другої.

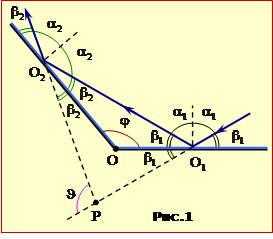
Показані також усі інші кути, що потрібні для розв’язування задачі.

Із рис. 1 видно, що кут відхилення \(\vartheta\) є зовнішнім кутом трикутника PO₁O₂, отже

\(\vartheta=2\beta_{1}+2\beta_{2}=2(\beta_{1}+\beta_{2})\).

А з  трикутника O₁OO₂ маємо

\(\beta_{1}+\beta_{2}=180^{\circ}-\varphi\),

Отже шуканий кут відхилення

\(\vartheta=360^{\circ}-2\varphi\).

В отриманій відповіді заслуговує на увагу те, що цей кут не залежить від напрямку падаючого променя й визначається тільки величиною двогранного кута \(varphi\). Зокрема, якщо \(\varphi=90^{\circ}\), то \(\vartheta=180^{\circ}\). Тобто, прямокутне двогранне дзеркало будь-які промені, що падають у перпендикулярній до його ребра площині, відбиває у зворотньому напрямі. А тригранне прямокутне дзеркало, як можна довести, має таку властивість  узагалі незалежно від напрямку падаючих променів. Це використовується у так званих кутових відбивачах, якими, зокрема, є катафоти автомобілів і велосипедів, а також рефлектори на ранцях школярів.

Задача 2.2

Визначити,

під яким кутом \(\alpha\) падає світло на межу поділу двох середовищ із відношенням показників заломлення k = 1,5, якщо відбитий та заломлений промені є взаємно перпендикулярні.

Дано: k = 1,5 \(\varphi=90^{\circ}\)

\(\alpha\) - ?

Розв’язання

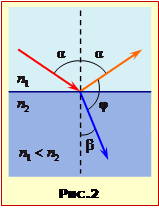Із рис. 2, на якому показано хід довільного променя при падінні світла на межу поділу з оптично менш густого середовища (n₁ < n₂), видно, що \(\alpha+\varphi+\beta=180^{\circ}\). Отже, при \(\varphi=90^{\circ}\) кут заломлення \(\beta=90^{\circ}-\alpha\), і $\sin \beta =\cos \alpha $. Тож за заоном заломлення (2.3)

$\frac{{{n}_{2}}}{{{n}_{1}}}=\operatorname{tg}\alpha $,

Числова відповідь  залежить послідовності проходження світлом середовищ, тож є два випадки:

1)    \(\frac{n_{2}}{n_{1}}=k\)     і    \(\alpha_{1}=\mathrm{arctg}{1,5}=56,3^{\circ}\);

2)    \(\frac{n_{2}}{n_{1}}=\frac{1}{k}\)   і  \(\alpha_{2}=\mathrm{arctg}\frac{1}{1,5}=33,7^{\circ}\).

Корисно звернути увагу на те, що одне з цих значень є кутом падіння, а інше – кутом заломлення, незалежно від послідовності проходження світлом середовищ.

 

Задача 2.3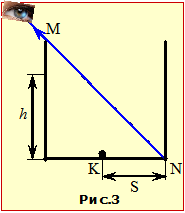

Спостерігач розглядає  порожню непрозору кубічну посудину з кулькою на дні так, що повністюбачить стінку посудини, але не бачить дна (рис. 3).

Визначити,

до якого найменшого рівня h слід наповнити посудину водою, аби спостерігач  побачив кульку, якщо вона знаходиться на відстані S = 10 см від видимого краю дна .

Дано: n = 1,33 S = 10 см

h - ?

Розв’язання

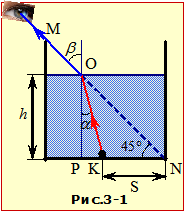З умови випливає, що, аби спостерігач бачив кульку, відбите нею світло має заломлюватися на поверхні води під заданим кутом β = 45° (див. рис 3-1) і падати на неї під відповідним кутом α, що за законом заломлення (2.3) задовольняє умову:

\(\sin\alpha=\frac{1}{n\sqrt{2}}\).

(1)

Отже, при заданому положенні кульки величина α по суті теж є відомою. Це дозволяє визначити потрібну висоту рівня води h з рис. 3-1, на якому довжина відрізка KN = S, враховуючи кут зору, PN = h, і

PK  = h – S.

У той же час 

PK = htg\(\alpha\),

тож, прирівнявши праві частини наведених виразів, отримаємо:

 $h=\frac{S}{1-\operatorname{tg}\alpha }$

Відтак, виразивши тангенс через синус і врахувавши значення (1), після нескладних викладок дістанемо відповідь:

$h=\frac{S}{1-\sqrt{2{{n}^{2}}-1}}$ \(=26,9\) см. 

В отриманій відповіді може здивувати, що потрібна висота рівня води не залежить від розмірів посудини. Але це пояснюєься кубічною формою посудини, через що при змінїї її розмірів кут зору,  тож і кут падіння променя на поверхню води, не змінюються. 

Задача 2.4

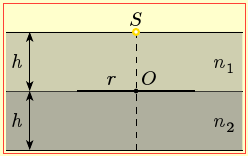
На поверхні дотику двох пластин з показниками заломлення n₁ = 1,35 i n₂ = 1,95 і товщиною по h = 2 см зафарбовано круг радіусом r = h.

Визначити 

радіус тіні R, яку відкидатиме круг на поверхню іншої пластини, якщо над його центром розмістити точкове джерело світла S на:

А) першій пластині;

В) другій пластині.

Дано: h = 2 см \(n_{1}\) = 1,35 \(n_{2}\) = 1,95

R - ?

Розв’язання

А) У цьому випадку світло переходить з оптично менш густого середовища в більш густе, й заломлюється,як показано на рис. 4-1а. За законом заломлення (1.3) радіус тіні

\(R=r+h\mathrm{tg}\beta\).

При цьому за умовою r  = h,

$R=h(1+\operatorname{tg}\beta )$,

тож, виразивши тангенс через синус, як

$\operatorname{tg}\beta =\frac{\sin \beta }{\sqrt{1-{{\sin }^{2}}\beta }}=\frac{1}{\sqrt{\left( 1/{{\sin }^{2}}\beta  \right)-1}}$,

дістанемо

$R=\left( 1+\frac{1}{\sqrt{\left( 1/{{\sin }^{2}}\beta  \right)-1}} \right)$.

За умовою α = 45°, отже величина \(1/\sin^{2}\beta\) за законом заломлення (2.4) складає

\(\frac{1}{\sin^{2}\beta}=\frac{2n_{2}^{2}}{n_{1}^{2}}\),

і шуканий радіус тіні

\(R=h\left(1+\frac{1}{\sqrt{2(n_{2}/n_{1})^{2}-1}}\right)\approx3,1\) см.

 

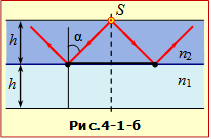Б) В цьому випадку світло падає на межу поділу з більш густого середовища, тому, перш ніж виконувати обчислення, слід з'ясувати, чи зможе світло взагалі пройти через межу поділу. Для цього за допомогою формули (1.4) знаходимо граничний кут для заданих речовин речовин:

\(\alpha_{0}=\mathrm{arcsin}\left(\frac{n_{1}}{n_{2}}\right)=43,8^{\circ}\).

Так що кут падіння (\(45^{\circ}\))крізь межу дотику пластин не пройде  жоден промінь (див. п. 2.2), і вся вона буде затінена.  Тож формально відповідь записується як

\(R\to\infty\).

 

Задача 2.5

Промінь світла під кутом \(\alpha=60^{\circ}\) падає  з повітря  на скляну плоскопаралельну пластину товщиною d = 3 см.

Дано: \(\alpha\) = \(60^{\circ}\) n = 1,5 d = 3 см

x - ?

Розв’язання

На рис. 5-1 із необхідними позначеннями показано хід променя крізь плоскопаралельну пластинку. Тож на основі  закону заломлення світла  (1.3) для верхньої та нижньої граней можна записати:

\(\frac{\sin\alpha}{\sin\beta}=n\),    \(\frac{\sin\beta}{\sin\alpha^{\prime}}=\frac{1}{n}\).

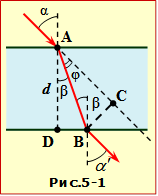
З цих виразів випливає, що \(\alpha^{\prime}=\alpha\), тобто промінь, не змінюючи напрякму, зміщується на певну відстань x = BC, яку треба визначити. 

Для отримання відповіді скористаємося рисунком 5.1, на якому трикутник ΔАВС є прямокутним із гіпотенузою АВ = (d/cosβ). тож

$x=AB·sinφ =\frac{d\sin \varphi }{\cos \beta }$,

де

$\varphi =\alpha -\beta $.

Далі, скориставшся формулою синуса різниці кутів, дістанемо:

$x=\frac{d\sin \left( \alpha -\beta  \right)}{\cos \alpha }$ = $d\frac{\sin \alpha \cos \beta -\cos \alpha \sin \beta }{\cos \beta }$ =

= $d\left( \sin \alpha -\cos \alpha \operatorname{tg}\beta  \right)$

У цьому виразі кут $\beta$ задовольняє закон заломлення світла. Тож,  виразивши $\operatorname{tg}\beta $ через $\sin \beta $, відповідно до закону заломлення (1.3), отримаємо остаточну відповідь:

 $x=d\sin \alpha \left( 1-\frac{\cos \alpha }{\sqrt{{{n}^{2}}-{{\sin }^{2}}\alpha }} \right)$ =\(1,53\) см.

 

Задача 2.6

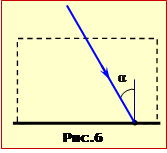Вузький паралельний пучок променів падає на аркуш паперу під кутом \(\alpha=60^{\circ}\) і створює світлову пляму (рис. 6).

Визначити

відстань  S на яку зміститься цятка, якщо на папір покласти скляну (n = 1,5) пластину товщиною d = 5 см.

Дано: α = 60° n = 1,5 d = 5 см

S - ?

Розв’язання

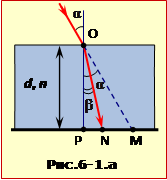Нехай спочатку світна цятка розміщена в точці M (рис. 6-1.а). Після того як на папір поклали пластину, цятка внаслідок заломлення переміститься в точку N.

Шукана відстань S = MN. З рисунка видно, що

S = PM – PN = \(d(\mathrm{tg}\alpha-\mathrm{tg}\beta)\).

(1)

Величину \(\mathrm{tg}\beta\) легко визначити через відомі тригонометричні співвідношення та закон заломлення (1.3), згідно з яким \(\sin\beta=\sin\alpha/n\)

\(d(\mathrm{tg}\beta=\frac{\sin\beta}{\cos\beta}=\frac{\sin\beta}{\sqrt{1-\sin^{2}\beta}}=\frac{\sin\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\).

Підставивши цей вираз у формулу (1), дістанемо відповідь:

\(S=d\left(\mathrm{tg}\alpha-\frac{\sin\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)\).

Обчислення дають:

\(S=5\cdot\left(\sqrt{3}-\frac{\sqrt{3}}{2\cdot\sqrt{1,5^{2}-3/4}}\right)\approx\) 5,1 см.

Одержати відповідь у цій задачі також можна інакше.

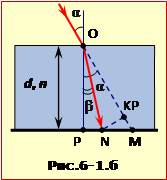Дійсно, якщо з точки N опустити перпендикуляр на лінію OM (рис. 16-2.б), то з трикутника NKM: NM = NK/\(\cos\alpha\). Відрізок NK = x був визначений у задачі 2.5 формула (4).

Отже маємо:

\(S=d\mathrm{tg}\alpha\left(1-\frac{\cos\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)=d\left(\mathrm{tg}\alpha-\frac{\sin\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)\).

 

Задача 2.7.

Рибалці в човні, котрий прямо під собою розглядає камінець на дні ставка, здається, що він знаходиться на глибині 3 м. 

Визначити

справжню глибину ставка H.

Дано: h= 3 м n = 1,33

H - ?

Розв’язання

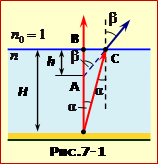Відповідно до закону заломлення світла (2.3), відбиті від камінця промені світла на виході з води заломлюються під більшим кутом, аніж падають, як показано на рис. 7-2. Тому при потраплянні в  око рибалки вони створюють хибне враження, що камінець знаходиться в т. А на глибині h, меншій ніж справжня глибина H. При цьому, як зрозуміло з рисунка,

$\frac{H}{h}=\frac{\operatorname{tg}\beta }{\operatorname{tg}\alpha }$

або, беручи до уваги малість кутів,

$\frac{H}{h}=\frac{\beta }{\alpha }$   $\Rightarrow $   $H=h\frac{\beta }{\alpha }$

де відношення кутів, згідно із законом заломлення (1.3а), дорівнює відношенню показників заломлення води n та повітря n₀ = 2. Отже, справжня глибина ставка

\(H=nh=4\) м.

 

 

Задача 2.8

Промінь, який падає на призму під кутом \(\alpha=30^{\circ}\) і виходить під кутом  \(\beta=60^{\circ}\), відхиляється на кут \(\delta=45^{\circ}\).

Визначити

заломний кут призми \(\varphi\).

Дано: α1 = 30° α2 = 60° δ = 45°

φ - ?

Розв’язання

Позначимо кут заломлення на першій грані \(\beta_{1}\), а кут падіння на другу грань \(\beta_{2}\) (рис.8-1).

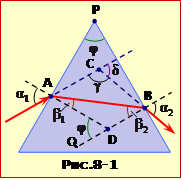Кут відхилення променя \(\delta\) – то є кут між напрямками променя, що вийшов з призми та променя, що падає на призму. Він є зовнішнім кутом трикутника ΔABC, отже

В цьому трикутнику \(\angle\)BAC = \(\alpha_{1}-\beta_{1}\) і \(\angle\)ABC = \(\alpha_{2}-\beta_{2}\). Тому

Прирівнюючи праві частини виразів (1) і (2), отримаємо:

Зовнішній кут \(\angle\)ADQ трикутника ABD дорівнює заломному кутові призми \(\varphi\), оскільки він утворений перпендикулярами до бічних граней призми. Отже

Підставивши цей вираз у формулу (3), дістанемо відповідь:

\(\delta=\alpha_{1}+\alpha_{2}-\varphi\)     \(\Rightarrow\)     \(\varphi=\alpha_{1}+\alpha_{2}-\delta=30^{\circ}+60^{\circ}-45^{\circ}\)

 

Задача 2.9

Промінь світла під малим кутом падає на бічну грань скляної призми із заломним кутом \(\varphi=0,1\) рад.

 

 кут відхилення \(\delta\) променя призмою.

 

Дано: φ = 0,1 рад n = 1,5

δ - ?

Розв’язання

Скористаємося результатами задачі 2.8 (формули (3) і (4)):

Відтак залишається визначити суму кутів \(\alpha_{1}\) та \(\alpha_{2}\). При малих кутах \(\sin\alpha\approx\alpha\), отже, за законом заломлення (1.3) можна наближено записати

де n – показник заломлення призми. Підставивши вирази (3) у формулу (1) і врахувавши співвідношення, (2) отримаємо:

\(\delta=n(\beta_{1}+\beta_{2})-(\beta_{1}+\beta_{2})=(n-1)\varphi\).

Таким чином, при малих кутах падіння кут відхилення променя в призмі з малим заломним кутом залежить тільки від показника заломлення та заломного кута.

Виконаємо обчислення:

\(\delta=(1,5-1)\cdot{0,1}=0,05\) рад = \(2,86^{\circ}\).

 

Задача 2.10

Промінь світла падає на бічну грань скляної призми із заломним кутом  \(\varphi=60^{\circ}\) і непрозорою основою. Визначити мінімальне значення кута падіння \(\alpha_{m}\), при якому світло проходитиме крізь призму.

Дано: n = 1,5 φ = 60°

αm - ?

Розв’язання

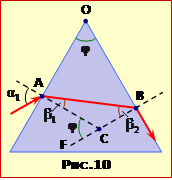На рис.10 показаний хід граничного променя крізь призму і відповідні кути.

Світло буде проходити крізь призму за умови

\(\beta_{2}\le\beta_{г}\),

(1)

де \(\beta_{г}\) – граничний кут, для якого відповідно до формули (2.7), умову (1) можна записати, як

\(\sin\beta_{2}\le\frac{1}{n}\).

З іншого боку (див. задачу 2.8, формула (4))

відповідно до цього світло проходить крізь призму за умови

\(\sin(\varphi-\beta_{1})\le\frac{1}{n}\).

З виразів (1) і (2) слідує, що найбільшій величині \(\beta_{1}=\beta_{г}\) відповідає таке значення \(\beta_{1}=\beta_{m}\), при якому

За законом заломлення (1.3) найменшому значенню \(\beta_{1}=\beta_{m}\) відповідає шуканий найменший кут падіння \(\alpha_{1}=\alpha_{m}\), причому

\(\sin\beta_{m}=\frac{\sin\alpha_{m}}{n}\).

Підставляючи цей вираз в рівність (3) і використовуючи відому тригонометричну формулу, одержимо

\(\frac{1}{n}=\sin\varphi\cdot\frac{1}{n}\sqrt{n^{2}-\sin^{2}\alpha_{m}}-\frac{1}{n}\sin\alpha_{m}\cos\varphi\)     \(\Rightarrow\)

\(\Rightarrow\)     \(1+\sin\alpha_{m}\cos\varphi=\sin\varphi\sqrt{n^{2}-\sin^{2}\alpha_{m}}\).

Зведемо останній вираз в квадрат і виконаємо перетворення:

\(\sin^{2}\alpha_{m}+2\sin\alpha_{m}\cos\varphi+1-n^{2}\sin^{2}\varphi=0\).

Рішення цього квадратного рівняння відносно \(\sin\alpha_{m}\)  дає

\(\sin\alpha_{m}=-\cos\varphi+\sqrt{\cos^{2}\varphi-1+n^{2}\sin\varphi}=-\cos\varphi+\sin\varphi\sqrt{n^{2}-1}\).

(Другий корінь не має фізичного змісту).

Виконаємо обчислення:

\(\sin\alpha{m}=-\cos{60^{\circ}}+\sin{60^{\circ}}\sqrt{1,5^{2}-1}\)     \(\Rightarrow\)      \(\alpha_{m}=27,9^{\circ}\).