ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс

◄ Предыдущая: 1.3. Дзеркала і лінзи Следующая: 2. Приклади розв’язування задач ►

Розділ I. Геометрична оптика

1.4. Загальні рекомендації з розв'язування задач

Побудова зображень

Задачі цього типу вимагають копіткої роботи й передбачають наступні "правила гри":

  • незалежно від кутів і відстаней на кресленнях, промені вважаються параксіальними (див. п. 1.3);
  • аби відобразити на кресленні тип і тонкість лінзи, її зображують у вигляді відрізка із стрілками, або "вилками" на кінцях (рис.16.13) для збиральної та розсіювальної лінзи, відповідно;
  • зображуваним предметом теж є стрілка (рис .16. 7, 16.10), отже побудова зображення полягає у графічному визначенні положення її кінців.
  • при побудові зображення, предмета, що дотикається до  головної оптичної осі лінзи (дзеркала) й розташований перпендикулярно,  дозволено не будувати зображення точки дотику;
  • при побудові зображення точки, що лежить на головній оптичній осі, заборонено додавати перпендикулярний допоміжний відрізок, зводячи  задачу до визначення зображення точки, що не лежить на осі;
  • побудова ходу променів виконується за допомогою тільки  лінійки  без використання шкали.
  • усі промені, що виходять з однієї точки, після проходження через лінзу (дзеркало) самі, чи їхні продовження, теж перетинаються в одній точці. Тож для отримання зображення точки достатньо двох променів, що виходять з неї.

При розв'язуванні задач на побудову зображень корисно керуватись такими порадами.

1.

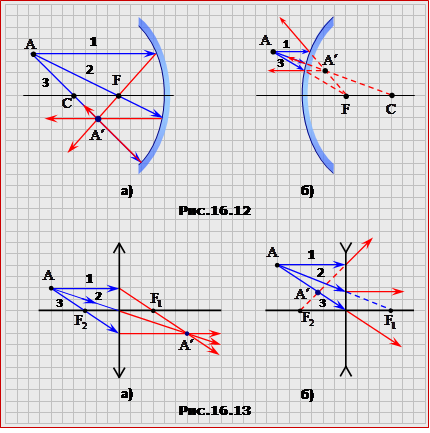
 Для побудови зображення А′  точки А  без вимірювань (рис.16.12 (на б) поставити 2), рис.16.13(2 і 3 поміняти місцями)) слід користатися трьома "зручними" променями, хід яких є заздалегідь відомий, а саме,

промінь 1, який іде паралельно до головної оптичної осі приладу;

промінь 2, який проходить через фокус;

промінь 3, який проходить через оптичний центр приладу.

 

 

2. 

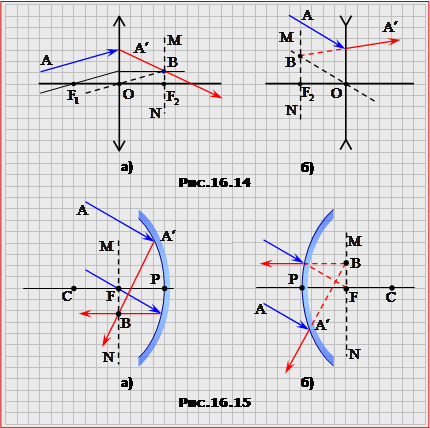
В деяких задачах за умовою можна використати тільки один з названих зручних променів (як, приміром, при побудові зображення точки, що лежить на головній оптичній осі (рис.16.11б). У такому разі за другий  приймають довільний промінь і будують його хід, як показано на рис. 16.14 і рис.16.15.( перенести А′, як на 16.14)

 Побудову слід виконувати в такій послідовності:

а) показати фокальну площина MN;

б) паралельно до заданого променя АА' провести один із ”зручних“ допоміжних променів і знайти точку його перетину В з фокальною площиною;

в) через точки А' і В провести шуканий допоміжний промінь.

 

 

3.

Однією з типових задач на побудову є визначення розташування та характеристик лінзи за заданими положеннями якоїсь точки та її зображення. При цьому

  • пряма, що проходить через точку A та її зображення A', перетинає головну оптичну вісь в центрі лінзи (дзеркала) С, рис.16.12, 16.13;
  • точка A та її дійсне зображення A' розташовуються по різні боки від головної оптичної осі (рис.16.12а, 16.13а), а при уявному зображенні – по один бік (рис.16.12б, 16.13б).

 

 

 

 Розрахункові задачі

А. Відбивання і заломлення світла. Розв'язуючи задачі такої тематики, варто пам'ятати наступне.

1)

Коли світло падає на межу поділу з оптично більш густого середовища, то, перш  ніж приступати до викладок, корисно знайти граничний кут і пересвідчитися, чи проходять промені крізь межу поділу середовищ, чи зазнають повного відбивання.

 

 

2)

Якщо за умовою кути падіння і заломлення малі (як це завжди є при візуальних спостереженнях), то при розв'язуванні задачі слід користуватися наближенням малих кутів \(\sin\alpha\approx\mathrm{tg}\alpha\approx\alpha\), і виражати їх у радіанах. Це значно спрощує викладки й обчислення, а інколи є й необхідною умовою отримання розв'язку.

В. Формула дзеркала й лінзи. Формули дзеркала (1.6) і тонкої лінзи (1.10) є ідентичні. Тому в обох випадках задачі на визначення характеристик зображень  розв'язуються за однаковою схемою. А саме, необхідно

1)

На ескізному рисунку показати орієнтовні положення лінзи (дзеркала), предмета і його зображення без ходу променів та позначити відповідні відстані. (У найпростіших ситуаціях цього можна не робити).

 

 

2)

Скласти робочі рівняння: записати формулу лінзи (дзеркала) з урахуванням додаткових умов задачі, таких, як задана відстань між предметом та екраном, збільшення, тощо. При цьому слід ураховувати правило знаків, зокрема те, що фокусні відстані  (або оптичні сили) вгнутого дзеркала і збиральної лінзи є завжди додатні, а опуклого дзеркала та розсіювальної лінзи – від'ємні. При цьому коли знак шуканої відстані не є очевидним, вона при викладках уважається додатньою. Істину покаже знак відповіді:  "+" означатиме дійсну, а "–" уявну величину.

 

 

3)

У деяких задачах складання рівнянь і розв'язування задачі полегшується, якщо скористатись оборотністю світлових променів, яка полягає в тому, що предмет та його зображення можна міняти ролями. Це випливає із законів відбивання та заломлення світла.

 

 

4)

Розв'язати отримане рівняння (або систему рівнянь) і знайти аналітичну відповідь (формулу), яка показує положення, розміри та характер зображення. Відтак за допомогою лінійки виконати креслення з побудовою ходу променів. Це потрібно для ілюстрації та перевірки правильності відповіді. (До прикладу, чи часом не вийшло, що за розрахунками зображення є уявне, а хід променів засвідчує протилежне).

◄ Предыдущая: 1.3. Дзеркала і лінзи Следующая: 2. Приклади розв’язування задач ►