ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
2. Приклади розв'язування задач
2.2. Дифракція світла
Задача 2.6. Видиме світло, що містить усі кольори від фіолетового (λ1 = 390 нм) до червоного (λ2 = 750 нм), після проходження крізь дифракційну ґратку потрапляє на екран. Визначити кількість дифракційних спектрів N, яку буде видно по один бік екрана.
Задача 2.7. Дифракційну ґратку, що містить n = 45 штрихів на 1 мм, опромінюють монохроматичним світлом. Визначити його довжину хвилі \(\lambda\), якщо кут між напрямами на головні дифракційні максимуми порядків m1 = 1 та m2 = 2 складає \(\Theta=1,6^{\circ}\).
Видиме світло, що містить усі кольори від фіолетового (λ1 = 390 нм) до червоного (λ2 = 750 нм), після проходження крізь дифракційну ґратку потрапляє на екран.
Визначити,
кількість дифракційних спектрів N, яку буде видно по один бік екрана.
|
Дано: λ1 = 390 нм λ2 = 750 нм |
|
N – ? |
Розв'язання
В умові не вказано відстань $h$ від ґратки до екрана та його ширину, тож може здатися, що задача є некоректна. Проте це не так, як показує аналіз залежносі від довжини хвилі $\lambda $ положення на екрані $Е$ (рис. 2.6)
$x=h\operatorname{tg}\varphi $
дифрагованих променів з різною довжиною хвилі, а саме. Зважаючи на специфіку функції $\operatorname{tg}\varphi $, при зміні кута дифракції і довжини хвилі в області великих значень зміна величини $x$ різко пришвидшується, так що довгохвильова зона дифракційнго спектра на екрані виявляється сильно розтягненою порівняно з корткохвильовою. Через це червона межа ((${{\lambda }_{2}}$)) одного спектра може опинитися від центра екрана далі, ніж фіолетова (${{\lambda }_{1}}$) наступного. В такому разі, через накладання променів з різною довжиною хвилі, в зоні перекриття впорядкованого розташування кольорів на екрані, тобто дифракційного спектра, не буде.
Отже, всупереч висловленим напочатку сумнівам, кількість спектрів, які можна побачити на екрані, залежить не від його розмірів і відстані до ґратки, а від межових кутів спектрів, які визначаються формулою (2.10). Зокрема, для сусідніх спектрів
$d\sin {{\varphi }_{2}}=m{{\lambda }_{2}}$
і
$d\sin {{\varphi }_{1}}=(m+1){{\lambda }_{1}}$,
де ${{\varphi }_{2}}$ і ${{\varphi }_{1}}$ – кути дифракції для червоних (${{\lambda }_{2}}$) променів у спектрі порядку $m$ та фіолетових (${{\lambda }_{1}}$) у наступному. При цьому умовою перекривання спектрів є
${{\varphi }_{2}}$ > ${{\varphi }_{1}}$,
отже,
m${{\lambda }_{2}}$ > (m+1)${{\lambda }_{1}}$.
Відтак, розв’язавши цю нерівність, отримаємо
$m$ > $\frac{{{\lambda }_{1}}}{{{\lambda }_{2}}-{{\lambda }_{1}}}$ $\Rightarrow $ $m$ > 1,1.
Позаяк за змістом число $m$ є ціле, отриманий розв'язок означає, що перекривання спектрів починається з другого порядку. Таким чином, на екрані буде видно весь спектр першого порядку й частину другого від початку до довжини хвилі ${{\lambda }}$, для якої кут дифракції ${{\varphi }}$ збігається з кутом дифракції ${{\varphi }_{1}}$ фіолетових променів (${{\lambda }_{1}}$) у спектрі третього порядку. Отже,
$\left\{ \begin{array}{*{35}{l}} {} & d\sin {{\varphi }_{1}}=2\lambda \\ {} & d\sin {{\varphi }_{1}}=3{{\lambda }_{1}} \\\end{array} \right.\quad \Rightarrow \quad \lambda =\frac{3}{2}{{\lambda }_{1}}=585$ нм,
що відповідає жовтому кольору.
Задача 2.7
Дифракційну ґратку, що містить n = 45 штрихів на 1 мм довжини, по нормалі опромінюють монохроматичним світлом.
Визначити
його довжину хвилі \(\lambda\), якщо кут між напрямами на головні дифракційні максимуми порядків m1 = 1 та m2 = 2 складає \(\Theta=1,6^{\circ}\).
|
Дано: n = 45 1/мм
m1 = 1
m2 = 2
Θ = 1,6°
|
|
λ - ?
|
Розв’язання
Відповідно до дифракційної формули (2.10),
| $d\sin \varphi ={{m}_{1}}\lambda $, |
(1) |
|
|
\(\d\sin(\varphi+\Theta)=m_{2}\lambda\), |
(2) |
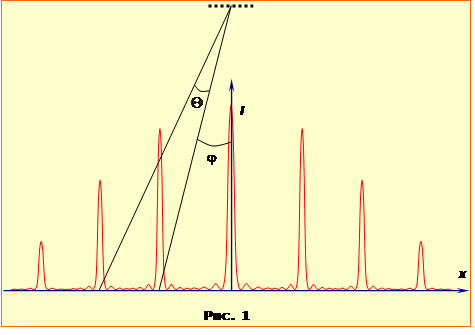
де \(\varphi\) – кут дифракції для першого і \(\(\varphi+\Theta)\) для другого головного максимума (рис.1), і d – період гратки, що визначається кількістю штрихів на одиницю довжини ґратки як
\(d=\frac{1}{n}\).
Далі подамо вираз (2) у вигляді
|
|
\(\frac{m_{2}\lambda}{d}=\sin\varphi\cos\Theta+\sin\Theta\cos\varphi\) |
|
і, зробивши заміну
\(\cos\varphi=\sqrt{1-\sin^{2}\varphi}\)
і, взявши до уваги, що 1,6° = 0,028 рад << 1, отже, \(\cos\Theta=1\) і \(\sin\Theta=\Theta\) (рад), отримаємо:
\(\frac{m_{2}\lambda}{d}=\sin\varphi+\Theta\sqrt{1-\sin^{2}\varphi}\).
Звідси, врахувавши, що за формулою (1)
\(\sin\varphi=m_{1}\lambda/d\),
після перетворень і обчислень дістанемо наступну загальну відповіль:
\(\lambda=\frac{\Theta}{N\sqrt{(m_{2}-m_{1})^{2}+m_{1}^{2}\Theta}}=\frac{\Theta}{N\sqrt{1+\Theta^{2}}}\approx\frac{\Theta}{N}\)
та числове значення шуканої довжини хвилі:
\(\lambda\approx{620}\) нм.