ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
1.Теоретичні відомості.
1.1. Рівняння координати та параметри гармонічних коливань
Визначальною рисою механічних гармонічних коливань є те, що вони відбуваються в обмеженій області простору й характеризуються строгою повторюваністю. Це відображує наступне рівняння координати при гармонічних коливаннях точки:
|
|
\(x={{x}_{m}}\cos \left( \frac{2\pi }{T}t+{{\varphi }_{0}} \right)\), |
(1.1) |
або
|
|
$x={{x}_{m}}\sin \left( \frac{2\pi }{T}t+{{\varphi }_{0}}^{\prime } \right)$, |
(1.1а) |
де \(\varphi_{0}^{\prime}=\varphi_{0}+\pi/2\).
Постійні величини xm, T, \(\varphi_{0}\) є параметрами – кількісними характеристиками – коливань і називаються, відповідно, амплітудою, періодом і фазою. Їхній зміст наочно ілюструє рис. 1.1
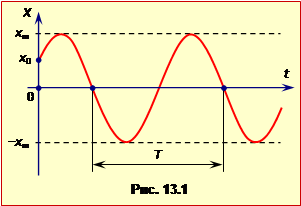
Амплітуда xm (її також часто позначають як А) – то є максимальне зміщення точки з положення рівноваги. Вона визначає "розмах" коливань: усі можливі значення координати коливної точки лежать в інтервалі \(\left[-x_{m},\ x_{m}\right]\).
Період T – це проміжок часу, протягом якого відбувається одне повне коливання, тобто час, через який рух точки в точності повторюється.
Періодичність руху при коливаннях характеризують також лінійною ν та циклічною (коловою) ω частотою.
Линійна частота дорівнює кількості коливань, що відбуваються за 1 с:
|
|
\(\nu=\frac{1}{T}\), |
(1.2) |
і вимірюється у герцах (Гц). 1 Гц = 1 с−1 – частота, при якій за 1 с відбувається одне коливання. При високих частотах використовують кілогерци (1 кГц = 103 Гц) і мегагерци (1 МГц = 106 Гц).
Циклічна (колова) частота є пов'язана з періодом і лінійною співвідношеннями:
|
|
\(\omega=\frac{2\pi}{T}=2\pi\nu\). |
(1.3) |
Циклічна частота вимірюється у радіанах за секунду (рад/с, або 1/с).
Використовуючи співвідношення (1.3), рівняння гармонічних коливань (1.1) можна записати через частоту:
|
|
\(x=x_{m}\cos(\omega{t}+\varphi_{0})\), |
(1.4) |
або
|
|
\(x=x_{m}\cos(2\pi\nu{t}+\varphi_{0})\) |
(1.4а) |
Фазою \(\varphi\) називається значення аргументу тригонометричної функції в наведених рівняннях:
\(\varphi=\frac{2\pi}{T}t+\varphi_{0}=\omega{t}+\varphi_{0}=2\pi\nu{t}+\varphi_{0}\).
Відповідно, величина ${{\varphi }_{0}}=\varphi \left( 0 \right)$ є початковою фазою коливань. Вона залежить від вибору моменту початку відліку часу й може мати будь-яке значення в інтервалі від 0 до \(2\pi\) рад.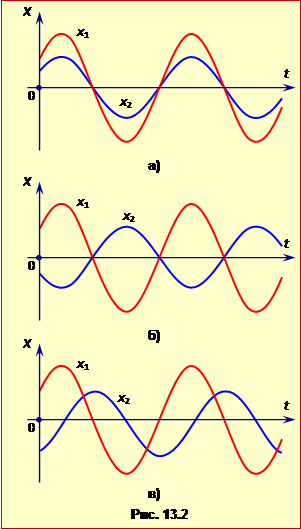
Фаза визначає поточний стан коливного тіла. Відповідно, різниця фаз \(\delta=\varphi_{01}-\varphi_{02}\) визначає узгодженість у часі коливань із однаковою частотою. Якщо різниця фаз \(\delta=0\) (рис.1.2а), то говорять, що коливання відбуваються "у фазі" або ''синфазно'', а при \(\delta=\pi\) (рис.1.2б) – "у протилежних фазах" або "в протифазі". В інших випадках говорять, що коливання відбуваються із "зсувом фаз" \(\delta\) (до прикладу, на рис.1.2б зсув фаз складає \(\pi\), а на рис.1.2в \(\delta=\frac{\pi}{2}\)).