ФІЗИКА. Вчимося розв'язувати задачі. "ЕЛЕКТРИКА І МАГНЕТИЗМ". Компенсаційний курс
Розділ І. Електричне поле
1.4. Зв’язок між напруженістю та потенціалом
Між напруженістю \(\vec{E}\) та потенціалом φ існує тісний зв’язок, який можна з'ясувати на прикладі роботи однорідного електричного поля \(\vec{E}\) = const на переміщенні $\Delta \vec{r}$ якогось заряду q між заданими точками 1 і 2 (рис. 1.8).
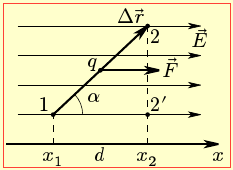
Ця робота через напруженість визначається як A = F·Δr·cosα = qE(x2 – x1) і як Α = q(φ1 − φ2) – через потенціал. Отже,
|
${{E}}=-\frac{{{\varphi }_{2}}-{{\varphi }_{1}}}{{{x}_{2}}-{{x}_{1}}}$, |
(1.19) |
або лаконічніше
|
$E=\frac{U}{d}$, |
(1.20) |
де E — модуль напруженості, U = φ1 − φ2 — спад напруги між точками 1 і 2, d = x2 – x1 — відстань між ними, відрахована в напрямку поля.
Аби сформулювати загальний зміст отриманого результату, зважимо на таке:
1. Вираз (1.19) є чинним при будь-якому взаємному розташуванні точок 1 і 2. При цьому коли кут α гострий (як на рис. 1.8), то φ1 > φ2, а коли тупий – навпаки, φ2 > φ1. Це означає, що в напрямку поля потенціал завжди зменшується.
2. При переміщенні заряду з т. 2 вздовж відрізка 2-2′ кут α = 90°, тож А = 0 і φ2 = φ2′. Це стосується й усіх інших точок площини, що проходить через т.2 перпендикулярно до напрямку поля.
3. Величина d = Δr·|cosα| є найменшою можливою відстанню між точками із заданою різницею потенціалів. Отже, вздовж напрямку поля швидкість зміни потенціалу Δφ/Δx є найбільшою.
Таким чином,
|
вектор напруженості електричного поля є скрізь напрямлений в бік найшвидшого зменшення потенціалу й по модулю дорівнює цій швидкості |
|
Слід зауважити, що це співвідношення встановлено тут для однорідного поля (\(\vec{E}\) = const ), тож у випадку неоднорідного поля (\(\vec{E}\) ≠ const) вираз (1.20) є непридатним для обчислень. Але, попри це, він якісно правильно відображає властивості поля й у загальному випадку. Зокрема те, що
|
про присутність електричного поля в заданій точці свідчить не наявність у ній певного потенціалу \(\varphi\), а лише його зміна \(\Delta\varphi\) ≠ 0 при переміщенні в сусідні точки. |
До прикладу, коли \(\varphi\ne{0}\), але \(\Delta\varphi=0\), то електричне поле відсутнє (\(\vec{E}=0\)). І навпаки, якщо в певній області простору із зарядженими тілами напруженість поля \(\vec{E}=0\), то це означає не нульову величину потенціалу, а лише його сталість (φ = const) у цій області.
Із співвідношення (1.20) також випливає, що
|
на межі двох середовищ не можливі стрибки потенціалу, |
бо це означало би необмежено велику напруженість поля.
Задля наочності електричне поле часто "зображують" на рисунку у вигляді сукупностей силових ліній та еквіпотенціальних поверхонь.
Силовою лінією (інакше – лінією поля) називається лінія, дотична до якої в кожній точці збігається з напрямом вектора напруженості поля в цій точці.
Еквіпотенціальною поверхнею (або поверхнею рівного потенціалу) називається поверхня, у всіх точках якої потенціал поля має однакове значення.
При будь-якому переміщенні еквіпотенціальною поверхнею у виразі (1.13) \(\cos\alpha=0\) і \(\alpha=90^{\circ}\). Це означає, що
|
силові лінії та еквіпотенціальні поверхні є взаємно ортогональні, тобто вектор \(\vec{E}\) у кожній точці поля спрямовано по нормалі до еквіпотенціальної поверхні, що проходить через цю точку. |
До прикладу, для поля точкового заряду (рис. 1.9 а, б) силові лінії є радіальними променями, а еквіпотенціальні поверхні – концентричними сферами (на рисунку – колами). Для однорідного поля силові лінії є паралельними рівновіддаленими променями, а еквіпотенціальні поверхні – перпендикулярними до них рівновіддаленими площинами (рис.1.9в). У зв'язку з цим зауважимо, що величина d у виразі (1.20) – то є відстань між двома заданими еквіпотенціальними поверхнями однорідного електричного поля.
