ФІЗИКА. Вчимося розв'язувати задачі. "ЕЛЕКТРИКА І МАГНЕТИЗМ". Компенсаційний курс: 1.3. Потенціал

ФІЗИКА. Вчимося розв'язувати задачі. "ЕЛЕКТРИКА І МАГНЕТИЗМ". Компенсаційний курс

◄ Предыдущая: 1.2. Принцип суперпозиції. Поле системи зарядів Следующая: 1.4. Зв’язок між напруженістю та потенціалом ►

Розділ І. Електричне поле

1.3. Потенціал

Потенціал. Сила, що діє на заряджену частинку в заданому електричному полі, визначається тільки величиною її заряду та координатами . Тому (див. [І], п. 4.2) робота поля при переміщенні частинки між будь-якими точками 1 і 2, не залежить від пройденого шляху і дорівнює спадові її потенціальної енергії:

A = W₁ – W₂.

(1.11)

Ця робота є прямо пропорційна силі (1.2), що діє на частинку, тож і її зарядові. Тому

відношення роботи А сил електричного поля зарядів при переміщенні зарядженої частинки між двома точками до її заряду q є характеристикою самого поля і називається різницею потенціалів (φ₁ − φ₂) між цими точками:

${{\varphi }_{1}}-{{\varphi }_{2}}=\frac{{{W}_{1}}-{{W}_{2}}}{q}=\frac{A}{q}$.

(1.12)

Указану різницю потенціалів інакше називають спадом напруги, або просто напругою й позначають одним символом:

φ₁ – φ₂ = U.

Отже, вираз роботи електростатичного поля при переміщенні заряду має вигляд:

Α = q(φ₁ − φ₂)

(1.13)

або

A = qU

(1.13а)

Різниця потенціалів (напруга) вимірюється у вольтах (В), 1 В = 1 Дж/Кл – це різниця потенціалів у таких двох точках поля, при переміщенні між якими заряду q = 1 Кл виконується робота A = 1 Дж.

Для елементарних частинок, зокрема електронів, джоуль є загрубою мірою роботи та енергії, й натомість використовують зручнішу позасистемну одиницю – електронвольт (еВ). За означенням

1 еB дорівнює енергії, що її отримує електрон у прискорювальному полі при переміщенні між точками з напругою 1 B.

Отже, згідно із формулою (1.13),

1 еВ = ${1,6}\cdot{10}^{-19}$ Дж.

Таким чином,

потенціал $\varphi$ є енергетичною характеристикою електричного поля.

Співвідношення (1.12) визначає тільки різницю потенціалів між заданими точками. А сам потенціал і потенціальна енергія є визначеними тільки відносно обраного нульового рівня – точки (чи множини точок), де потенціал приймається рівним нулю. Зважаючи на це, можна дати наступне означення:

потенціалом $\varphi$ електричного поля називається відношення його роботи A₀ при переміщенні частинки з даної в нульову точку до її заряду q:

$\varphi=\frac{A_{0}}{q}$.

(1.14)

Інакше кажучи,

потенціал $\varphi$ чисельно дорівнює роботі поля при переміщенні одиничного позитивного заряду з даної точки в нульову точку.

При цьому вибір нульової точки є довільним і визначається лише міркуваннями зручності. До прикладу, в електротехніці та електроніці нульову точку потенціалу обирають на земній поверхні, а в фізиці – на "на нескінченності", тобто в точках, що знаходяться безмежно далеко від зарядів, які створюють поле.

Обчислення потенціалу ґрунтується на принципом суперпозиції, за яким

потенціал φ поля довільної системи зарядів у кожній точці дорівнює сумі потенціалів φ_і полів складових частин системи:

$\varphi=\varphi_{1}+\varphi_{2}+…+\varphi_{n}$$=\sum{{{\varphi }_{i}}}$.

(1.15)

Для маленького зарядженого тіла (точкового заряду) потенціал визначає наступна

формула потенціалу поля точкового заряду:

$\varphi =k\frac{q}{\varepsilon r}=\frac{q}{4\pi {{\varepsilon }_{0}}\varepsilon r}$,

(1.16)

або

$\varphi =k\frac{q}{\varepsilon r}$, k = (1/4πε₀) = 9·10⁹ Ф/м.

(1.16а)

Отже, для потенціалу поля системи точкових зарядів маємо:

$\varphi =k\sum{\frac{{{q}_{i}}}{\varepsilon {{r}_{i}}}}$.

(1.17)

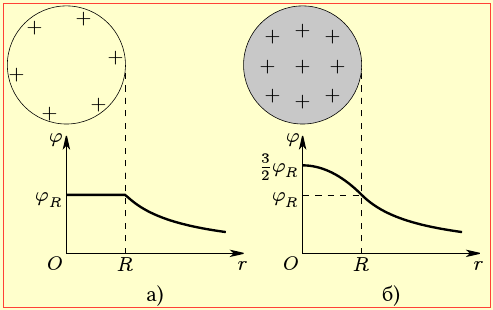
За розглянутою схемою визначають і потенціал поля протяжного зарядженого тіла: спочатку його ''розбивають'' на малі (точкові) ділянки, а потім відповідно до виразу (1.15) методами вищої математики визначають сумарний потенціал і за симетричного розподілу заряду отримують відповідну формулу. Зокрема,

потенціал поля сфери радіуса R із зарядом q, який рівномірно розподілено по поверхні або об'єму, назовні (на відстанях r ≥ R від центра) збігається з потенціалом поля точкового заряду, розміщеного в центрі, й за формулами (1.16) та (1.16а), відповідно, дорівнює

$\varphi=\frac{q}{4\pi\varepsilon\varepsilon_{0}r}$ або

$\varphi =k\frac{q}{\varepsilon{r}}$, k = (1/4πε₀) = 9·10⁹ Ф/м.

(1.18)

Всередині через відсутність поля (див. п. 1.2) потенціал є скрізь однаковий і збігається з потенціалом поверхні:

${{\varphi }_{R}}=k\frac{q}{R}$.

(1.18а)

Графік залежності φ(r) для поля сфери показано на рис. 1.9 а.

Такою самою (1.18) є й залежність φ(r) назовні (r ≥ R) рівномірно зарядженої по об'єму провідної кулі, позаяк в ній надлишковий заряд завжди зосереджено на поверхні.

Вираз (1.18) і відповідний графік φ(r) лишаються чинними й назовні (r ≥ R) рівномірно зарядженої по об'єму кулі з діелектрика. Але всередині через зменшення напруженості потенціал у напрямку центра зростає, як показано на рис. 1.7.