ФІЗИКА. Вчимося розв'язувати задачі. "ЕЛЕКТРИКА І МАГНЕТИЗМ". Компенсаційний курс
Розділ І. Електричне поле
1.2. Принцип суперпозиції. Поле системи зарядів
Дослід свідчить, що електричні поля не взаємодіють між собою – вони діють на заряди, але не одне на одного. Це відображує принцип суперпозиції, за яким
|
вектор напруженості електричного поля довільної системи зарядів у кожній точці дорівнює сумі векторів напруженості полів, створюваних у цій точці кожним із зарядів системи окремо (за відсутності інших): |
||
|
|
\(\vec{E}=\vec{E}_{1}+\vec{E}_{2}+…+\vec{E}_{n}=\sum\limits_{i=1}^{n}\vec{E}_{i}\). |
(1.7) |
Принцип суперпозиції разом із законом Кулона дозволяє визначати характеристики полів, що створюються як дискретними сукупностями зарядів, так і протяжними зарядженими тілами.
Поле системи точкових зарядів можна розрахувати безпосередньо за виразом (1.7). Для цього в ньому слід за формулою (1.6) визначити модулі Еі та додати самі вектори \(\vec{E}_{i}\), як це ілюструє рис. 1 .4 для найпростішої системи – двох точкових зарядів.

Подібно розраховують і поле протяжного зарядженого тіла: його подумки поділяють на елементарні (точкові) ділянки, відтак на основі формули (1.6) записують вираз напруженості поля окремої ділянки і відповідними математичними методами додають (інтегрують) напруженості полів усіх ділянок. При цьому для тіл правильної форми із симетричним розподілом заряду виходять прості загальні формули, як у наступних прикладах.
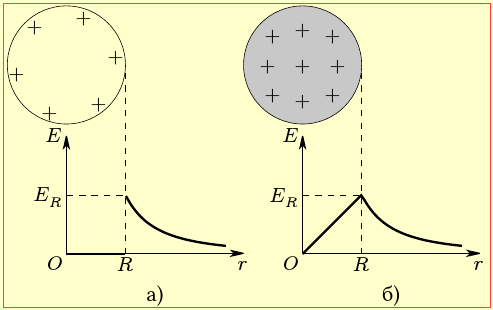
Поле сферичної оболонки. При рівномірному розподілі заряду q по поверхні сфери радіуса R створюється електричне поле, що скрізь має радіальний напрям і назовні (на відстанях r ≥ R від центра) збігається з полем розміщеного в центрі точкового заряду такої самої величини q і має таку саму напруженість E (формула (1.6)). Зокрема на поверхні
|
$E_{R}=\frac{q}{4\pi {{\varepsilon }_{0}}R^{2}}$. |
(1.8) |
Всередині сфери (r < R), як показано на рис. 1.5а, поле відсутнє:
|
$\vec{E}$ = 0. |
(1.8а) |
Поле кулі радіуса R із рівномірно розподіленим по об'єму зарядом q назовні (на відстанях від центра r ≥ R ) теж збігається з полем точкового заряду й визначається формулою (1.6), а всередині (r < R) лінійно зростає від 0 в центрі до значення (1.8) на поверхні (рис. 1. 5б).
Стосовно наведених положень варто сказати наступне. Радіальний напрям полів розглянутих тіл легко встановити на основі принципу суперпозиції, подумки розсікаючи їх паралельними площинами на множину кілець чи дисків, і враховуючи, що поля таких складових елементів є спрямовані вздовж діаметра сфери чи кулі. Що ж до формул, то отримати їх методами елементарної фізики не можна. Але на підтримку виразу (1.8а) можна вказати, що всередині будь-якої зарядженої замкненої поверхні напрямки полів двох малих ділянок на кінцях однієї хорди є зустрічними.
Поле рівномірно зарядженої нескінченної площини. З огляду на міркування симетрії можна зрозуміти, що таке поле є однорідне (\(\vec{E}\) = const) і спрямоване перпендикулярно до площини (рис. 1.6а). Величина його напруженості визначається наступною простою формулою, яку, проте теж не можна отримати елементарно:
|
|
$E=\frac{\sigma }{2{{\varepsilon }_{0}}\varepsilon }$, |
(1.9) |
де
|
|
$\sigma =\frac{\Delta q}{\Delta S}$ |
|
– поверхнева густина заряду (Кл/м2), тобто заряд, що припадає на одиницю площі зарядженої поверхні.
Примітка. Нескінченна площина – то є абстракція. Проте практично таке саме поле створює й реальна плоска пластина на малих порівняно з її розмірами відстанях.
У випадку двох паралельних заряджених площин напруженість поля за принципом суперпозиції визначається як \(\vec{E}\) = \(\vec{E}_{1}\) + \(\vec{E}_{2}\) і є не однаковою між та поза пластинами. Зокрема, напруженість поля плоского конденсатора (див. п.1.5), де знаки зарядів є різні, а величина σ однакова, поле поза пластинами відсутнє, а між ними – спрямоване від ”+“ до ”–“ (рис. 1.6б) і має напруженість рівну подвоєній напруженості поля одної пластини:
|
$E=\frac{\sigma }{{{\varepsilon }_{0}}\varepsilon }$. |
(1.10) |