ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Задачі для самостійної роботи
Рівновага довільного тіла
Рівень Б
|
5.57. |
Під яким найменшим кутом до горизонту може стояти драбина, приставлена до гладенької вертикальної стіни, якщо коефіцієнт тертя драбини по підлозі дорівнює \(\mu\)? Вважати, що центр ваги знаходиться посередині драбини. [\(\mathrm{arctg}(2\mu)\)] |
|
5.58. |
Людина масою 60 кг підіймається легкою драбиною довжиною 4 м, що приставлена до гладенької стіни під кутом \(\alpha=30^{\circ}\). На яку висоту може піднятися людина, якщо максимальна сила тертя спокою між драбиною і підлогою дорівнює 200 Н? [2 м] |
|
5.59. |
Куб маси m стоїть на горизонтальній площині. При якому мінімальному коефіцієнті тертя куб можна перекинути через ребро горизонтальною силою, перпендикулярною до ребра? Чому вона дорівнює? [0,5; mg/2] |
|
5.60. |
Якою найменшою силою та при якому найменшому коефіцієнті тертя можна перекинути через ребро куб маси 50 кг, що лежить на горизонтальній площині? [177 H; 1/3] |
|
5.61. |
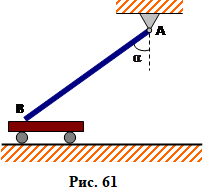
Однорідний стрижень маси m, шарнірно закріплений одним кінцем, іншим спирається на візок, утворюючи з вертикаллю кут \(\alpha\), рис. 61. Якою найменшою горизонтальною силою візок можна зрушити при коефіцієнт тертя між ним і стрижнем \(\mu\): а) ліворуч; б) праворуч? $\left[ a)\frac{\mu mg}{2\left( 1+\mu \operatorname{ctg}\alpha \right)}; б)\frac{\mu mg}{2\left( 1-\mu \operatorname{ctg}\alpha \right)},\mu <\operatorname{tg}\alpha \right]$
|
|
5.62. |
|
|
5.63. |
Котушку з мотком ниток, яка лежить на шорсткому столі, починають горизонтально тягти за довгий вільний кінець нитки. Як поведеться котушка: буде намотуватися на нитку, чи розмотуватись? |
|
5.64. |
Котушку тягнуть за нитку по столу зі сталою швидкістю так, що вона не обертається. Вказані на рис. 64 розміри котушки є задані. 1. Який кут \(\varphi\) утворює нитка з горизонтом? 2. Чому дорівнює сила натягу нитки F при масі котушки з нитками m і коефіцієнті тертя ковзання котушки \(\mu\)? $\left[ \varphi =\arccos \frac{r}{R};\quad F=\frac{mg}{\mu +\operatorname{ctg}\varphi } \right]$
|
Рівень B
|
5.65. |
|
|
5.66. |
|
|
5.67. |
|
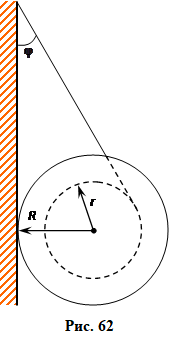 Котушка з нитками, підвішена до стіни (рис. 62), перебуває в рівновазі. При якому найменшому коефіцієнті тертя між котушкою й стіною це є можливо, якщо кут між ниткою й стіною
Котушка з нитками, підвішена до стіни (рис. 62), перебуває в рівновазі. При якому найменшому коефіцієнті тертя між котушкою й стіною це є можливо, якщо кут між ниткою й стіною 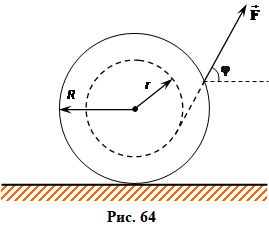
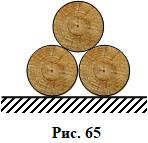 На дві однакові колоди, що впритул
На дві однакові колоди, що впритул 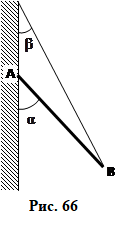 Однорідний стрижень
Однорідний стрижень 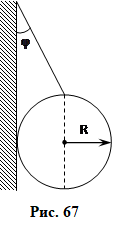 Куля радіусом R = 30 см і масою m = 7 кг , яку підвішено д
Куля радіусом R = 30 см і масою m = 7 кг , яку підвішено д