ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Задачі для самостійної роботи
Рівновага тіла, що не може обертатися
Рівень А
|
5.20. |
Два хлопці, перетягаючи канат, прикладають до його кінців протилежно спрямовані сили величиною F і 1,5F . Чому дорівнює сила натягу каната? [F] |
|
5.21. |
Тіло на горизонтальній поверхні перебуває в спокої, коли прикладена до нього горизонтальна сила не перевищує 1 H. Коефіцієнт тертя між тілом та поверхнею \(\mu=0,1\). Визначити вагу тіла. [10 H] |
|
5.22. |
Через прикріплений до стелі блок перекинули мотузку, один кінець якої закріплено на підлозі, а до іншого прив'язано тягар масою 10 кг. Визначити силу, з якою блок діє на стелю. [200 H] |
|
5.23. |
До середини мотузки, кінці котрої закріплено на однаковій висоті, підвісили тягар масою 15 кг. Визначити силу натягу мотузки, якщо провис її частин складає 30° до горизонту. [150 H] |
|
5.24. |
Довести, що ніяку мотузку чи трос неможливо натягнути строго горизонтально. |
|
5.25. |
Канат, який лежить на столі, частково звисає. Визначити коефіцієнт тертя між канатом і столом, якщо при звисанні на 25% довжини він починає зісковзувати. [1/3] |
|
5.26. |
Дошку, на якій лежить брусок, підіймають за один кінець. При якому куті нахилу дошки до горизонту брусок почне ковзати, якщо при коефіцієнт тертя складає 0,25? [\(14^{\circ}\)]. |
|
5.27. |
З якою найменшою горизонтальною силою треба притискати брусок маси 5 кг до вертикальної стіни, аби запобігти його зісковзуванню при коефіцієнті тертя 0,1? [500 H] |
|
5.28. |
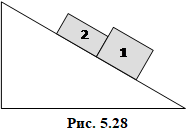
На похилу площину поклали два бруски (рис. 5.18) масами m1 = 1 кг і m2 = 0,6 кг. Коефіцієнти тертя між брусками та поверхнею \(\mu_{1}=0,3\) і \(\mu_{2}=0,1\). Визначити максимальний кут нахилу площини, при якому бруски ще не будить ковзати. [\(\alpha=12,7^{\circ}\)]
|
|
5.29. |
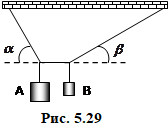
Підвішені на нитках тягарці А і В з'єднали горизонтальною нитяною перетинкою, як показано на рис. 5.19. Кути складають: \(\alpha=60^{\circ}\), \(\beta=30^{\circ}\). Знайти масу тягаря В, якщо маса тягаря А дорівнює 3 кг. [2 кг]
|
Рівень Б
|
5.30. |
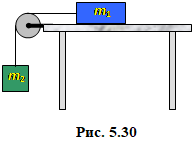
Вантажі m1 = 2 кг і m2 = 1 кг з'єднані ниткою, перекинутою через блок на краю стола (рис. 5.9) і перебувають у рівновазі. Визначити: а) силу тертя, що діє на вантаж m1 і б) силу реакції осі, що діє на блок. [10 Н; 14 Н]
|
|
5.31. |
Сила тертя, що діє на тіло маси 1 кг, яке лежить на похилій площині, дорівнює 6 H. Визначити силу нормальної реакції опори, що діє на нього. [8 H] |
|
5.32. |
На тіло, що лежить на столі, діють спрямовані під кутом \(120^{\circ}\) одна до одної горизонтальні сили F1 = 1,0 H, F2 = 2,0 H і F3 = 3,0 H. Визначити величину та напрям сили тертя, котра діє на тіло. [1,73 H, \(30^{\circ}\) до напрямку F1] |
|
5.33. |
Посередині вулиці треба підвісити на тросі ліхтар маси 10 кг так, аби його висота над землею була не меншою, ніж 5 м при висоті стовпів 6 м і відстані між ними 10 м. Якої мінімальної міцності трос для цього можна взяти? [250 H]. |
|
5.34. |
Якою горизонтальною силою F треба притискати брусок масою 1 кг до похилої площини з кутом нахилу до горизонту \(\alpha=30^{\circ}\), аби він перебував у рівновазі при коефіцієнті тертя о,1? [4,8 H ≤ F ≤ 6,8 Н] |
|
5.35. |
|
|
5.36. |
|
|
5.37. |
|
|
5.38. |
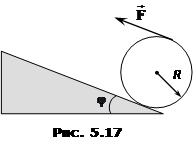
Циліндр маси m утримують у рівновазі на похилій площині з кутом нахилу \(\varphi\) паралельною до неї силою $\vec{F}$, рис. 5.17. Визначити: а) мінімальний коефіцієнт тертя, при якому це є можливо, і б) величину F . [а) \(\mu\ge(1/2)\mathrm{tg}\varphi\)]; б) \((mg/2)\sin\varphi\)
|
|
5.39. |
Визначити відношення жорсткостей пружин, якщо жорсткості їхнього паралельного та послідовного з'єднань відносяться, як 4,5 : 1. [2] |
|
5.40. |
Циліндр маси M за кінець намотаної на нього нитки утримують на горизонтальній підставці. Підставку прибирають і одночасно починають тягти вгору за нитку так, що циліндр лишається на незмінній висоті. Визначити силу натягу нитки і чи буде вона зрівноважувати силу тяжіння. [Mg, ні] |
|
5.41. |
Куля масою 5 кг спирається на дві гладкі похилі площини з кутами нахилу 35° і 20° до горизонту. З якою силою вона тисне на кожну з площин? [20 H; 34 H] |
|
5.42. |
Балку масою 1000 кг і довжиною 2 м горизонтально підвісили на двох тросах однакової довжини, один з яких закріплено за кінець балки, а інший – на відстані a = 25 см від її протилежного краю. Знайти натяг кожного троса. [5,5 кН; 4,2 кН] |
|
5.43. |
До гладкої вертикальної стіни на нитці довжиною 4 см підвішено кулю масою 300 г і радіусом 2,5 см. Визначити силу тиску кулі на стіну. [1,25 Н] |
Рівень B
|
5.44. |
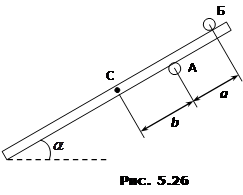
Дошка знаходиться між двома горизонтальними стрижнями А і Б, рис. 5.26. Кут α = 30°, a = 10 см, b = 15 см (т. С – центр ваги). При якій величині коефіцієнта тертя μ між стрижнями та дошкою вона перебуватиме в спокої? [ μ ≥ 0,143]
|
|
5.45. |
Людина масою m тягне на себе за мотузку ящик масою M, який лежить на підлозі. Коефіцієнт тертя між людиною з ящиком та підлогою дорівнює μ. Яку мінімальну силу має прикладати людина, аби тягти ящик? [\(0,5g\sqrt{(M-m)^{2}+\mu(M+m)^{2}}\)] |
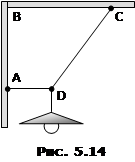 Ліхтар вагою P = 50 H закріплено двома шнурами, як показано на рис. 5.
Ліхтар вагою P = 50 H закріплено двома шнурами, як показано на рис. 5.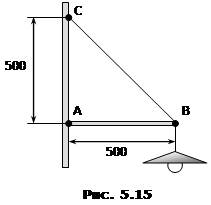 Ліхтар вагою P = 50H на горизонтальному шарнірному упорі АВ
Ліхтар вагою P = 50H на горизонтальному шарнірному упорі АВ 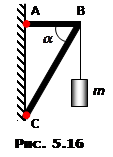 На кронштейні (рис. 5.16) висить вантаж масою m = 100 кг. Визначити сили, що діють на стрижні AB і BC, якщо вони утворюють кут
На кронштейні (рис. 5.16) висить вантаж масою m = 100 кг. Визначити сили, що діють на стрижні AB і BC, якщо вони утворюють кут