ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв’язування задач
Динаміка рівномірного руху по колу
Рівень А
|
2.81. |
На якій максимальній відстані від центра горизонтального диска, що обертається навколо своєї осі з частотою 33 об/хв, може лежати шайба при коефіцієнті тертя між нею й диском 0,2? [≈17 см] |
|
2.82. |
Байкер рухається по опуклому мосту круглого профілю радіусом 100 м. При якій найменшій швидкості байк на вершині мосту перестане тиснути на нього? [≈98,5 км/год] |
|
2.83. |
По опуклому мосту з радіусом кривини 50 м зі швидкістю 36 км/год рухається авто масою 1 т. З якою силою воно тисне на середину мосту? [8 кH] |
|
2.84. |
Авто маси 2 т рухається зі швидкістю 36 км/год угнутим мостом із радіусом кривини 100 м. З якою максимальною силою авто тисне на міст? [22 кH] |
|
2.85. |
Лижник із сталою швидкістю 10 м/с рухається прямою трасою спочатку по опуклій, а потім по угнутій ділянках однакового радіуса кривини 20 м. У скільки разів відрізняється вага лижника у найвищій та найнижчій точках шляху? [3] |
|
2.86. |
Кулю, що прикріплена до кінця легкого стрижня, рівномірно обертають у вертикальній площині. Визначити масу кулі, якщо різниця сил натягу стрижня при його вертикальному розташуванні складає 20 Н. [1 кг] |
|
2.87. |
Кулю, прикріплену до кінця легкого стрижня довжиною 80 см, рівномірно обертають у вертикальній площині. Знайти максимальну можливу частоту обертання (об/с), якщо стрижень витримує потрійну вагу кулі. [0,8 об/с] |
|
2.88. |
Гирю масою 500 г, прив'язану до мотузки довжиною 1 м, обертають у вертикальній площині з частотою 3 об/с. Визначити силу натягу мотузки у найнижчій та найвищій точках траєкторії. [183 H; 173 H] |
|
2.89. |
Кульку на нитці довжиною l = 1 м обертають по колу в горизонтальній площині так, що нитка утворює кут 45° із вертикаллю. Знайти швидкість і період обертання кульки. [2,6 м/с; 1,7 с] |
|
2.90. |
З якою максимальною швидкістю можна обертати в горизонтальній площині кулю масою 2 кг на нитці завдовжки 1 м, яка витримує навантаження до 100 H? [7 м/с] |
Рівень Б
|
2.91. |
Горизонтальний диск, на якому на відстані 16 см від осі лежить тіло масою 250 г, починають розкручувати з прискоренням 0,5 рад/с2. А) визначити, при якій кутовій швидкості обертання та через який час тіло почне ковзати по диску; Б) побудувати графік залежності радіальної складової сили тертя, що діє на тіло, від його кутової швидкості. [А) 5 рад/с; Б) натисніть ліву кнопку "миші"] |
|
2.92. |
Порожнисту кулю із внутрішнім радіусом 2 м обертають навколо вертикальної осі з частотою n = 30 об/хв. На якій висоті від дна встановилася вміщена в кулю кулька, що обертається разом з нею? [1 м] |
|
2.93. |
По опуклому мосту радіусом кривини 90 м зі швидкістю 54 км/год рухається авто масою 2 т. У точці мосту, напрям від якої до центра кривини мосту складає кут \(\alpha\) з вертикаллю, авто тисне на міст із силою 14,4 кH. Визначити величину \(\alpha\). [\(8,2^{\circ}\)] |
|
2.94. |
Швидкість байка 54 км/год, коефіцієнті тертя між шинами та покриттям автодрому 0,3. Якого найменшого радіуса віраж може закласти байкер та на який кут від вертикалі він має при цьому нахилитись? [76,5 м; ≈17°] |
|
2.95. |
Потяг рухається зі швидкістю 72 км/год колією ширини 1,5 м. Визначити, на скільки зовнішня рейка має бути розташована вище за внутрішню на закругленні радіусом 800 м, аби колеса не чинили бічного тиску на рейки. [7,65 см] |
|
2.96. |
Байкер рухається по вертикальній циліндричній стіні діаметром d = 10 м. Якою має бути найменша швидкість байка, аби він не впав при коефіцієнті тертя між колесами та стіною 0,3? [65,7 км/год] |
|
2.97. |
|
|
2.98. |
|
|
2.99. |
Радіус Місяця приблизно в 3,7 рази, а маса у 81 разів є менші, ніж у Землі. Визначити прискорення вільного падіння на Місяці. [1,66 м/с2] |
|
2.100. |
Яку тривалість мала би доба на Землі, якби тіла на екваторі були би невагомі? [1,41 год] |
|
2.101. |
Чому дорівнює перша космічна швидкість для планети, маса і радіус якої є вдвічі більші, ніж у Землі. [16,8 км/год] |
|
2.102. |
Чому дорівнює висота орбіти штучного супутника Землі, якщо його орбітальна швидкість складає 7,5 км/с? [700 км] |
|
2.103. |
Визначити першу космічну швидкість для планети з такою густиною, як у Землі, але з удвоє меншим радіусом. [≈4 км/с] |
|
2.104. |
Обчислити першу космічну швидкість для Місяця, якщо на ньому прискорення вільного падіння є в 6 разів менше за земне. Радіус Місяця є в 3,7 рази менший за радіус Землі. [1,68 км/с] |
|
2.105. |
Визначити висоту орбіти та лінійну швидкість геостаціонарного штучного супутника, тобто такого, що рухається в екваторіальній площині без зміни положення відносно поверхні Землі. [≈36,6 тис. км; 3,1 км/с] |
|
2.106. |
Визначити середню густину планети радіусом 10000 км, якщо швидкість її супутника на коловій орбіті радіусом 105 км дорівнює 4,1 км/с. [6 г/см3] |
Рівень В
|
2.107. |
У вагоні потяга, що рухається зі швидкістю 72 км/год по закругленню радіусом 200 м, зважують на пружинних вагах вантаж масою 5 кг. Якої відносної похибки (%) при цьому припускаються? [2%] |
|
2.108. |
$\left[ F=\frac{{{m}_{1}}{{m}_{2}}{{v}^{2}}}{\left( {{m}_{1}}+{{m}_{2}} \right)l} \right]$ |
|
2.109. |
Підвішена до стелі на гумовій нитці кулька маси m рухається в горизонтальній площині по колу так, що нитка утворює з вертикаллю заданий кут \(\alpha\). Чому дорівнює кутова швидкість ω кульки, якщо довжина не розтягненої нитки та її жорсткість складають l0 і k, відповідно. $\left[ \omega =\sqrt{\frac{kg}{mg+k{{l}_{0}}\cos \alpha }} \right]$ |
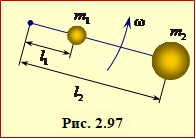 Дві кульки маси m1 = 50 г і m2 = 100 г
Дві кульки маси m1 = 50 г і m2 = 100 г 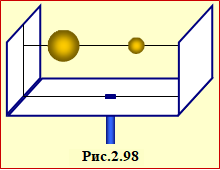 Намистинки (матеріальні точки) масами m1 і m2 = 2m1 нанизали на горизонтальну спицю,
Намистинки (матеріальні точки) масами m1 і m2 = 2m1 нанизали на горизонтальну спицю, 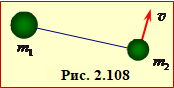 Дві кулі масами
Дві кулі масами