ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
2. Приклади розв'язування задач
2.6. Обертовий рух. Кочення.
Задача 1.26. Авто рухається по колу радіуса R = 250 м зі сталою швидкістю v = 36 км/год. Визначити залежність від часу: 1. Модуля переміщення та побудувати графік \(\left| \Delta \vec{r}\left( t \right) \right|\); 2. Координат x(t), y(t); 3. Проєкцій швидкості vx(t), vy(t) і прискорення ax(t), ay(t) та обчислити їхні модулі.
Задача 1.27. Диск рівномірно обертається навколо своєї осі, котра рухається горизонтально зі сталою швидкістю v0 = 2 м/с. Визначити швидкість v2 заданої точки 2 диска, якщо швидкість заданої точки 1 дорівнює v1 = 1 м/с.
Задача 1.28. Колесо радіуса R котиться горизонтальною площиною без ковзання зі швидкістю \( {v}_{0}\). Визначити швидкість v та прискорення \( {a}\) указаної точки на ободі, якщо її радіус обертання складає кут \( \alpha \) із вертикаллю.
Задача 1.29. Котушка радіуса R із шаром ниток радіусом r лежить на шорсткій горизонтальній поверхні. Визначити, в якому напрямі та з якою швидкістю u покотиться котушка, якщо нитку горизонтально потягнути за вільний кінець із швидкістю \( {v}\).
Задача 1.30. Із указаної точки на ободі колеса радіуса R, яке котиться горизонтальною площиною без ковзання, відлітає кусочок бруду. Визначити найменшу швидкість u колеса, при якій бруд знов потрапить у ту саму точку колеса при такому самому її розташуванні відносно осі.
Задача 1.31. Два тягарці різної маси, що з'єднані ниткою, перекинутою через нерухомий блок радіуса R, спочатку утримують на одному рівні, а потім вивільнюють. Відтак вони без ковзання нитки за час τ = 1 с розійшлися на відстань nR один від одного. Визначити кут повороту блоку \( \varphi \) та набуте за цей час прискорення \( \vec{a}\) указаною точкою, якщо R = 10 см і n = 3.
| Задача 1.25 |
| Задача 1.26 |
Авто рухається по колу радіуса R = 250 м зі сталою швидкістю v = 36 км/год.
Визначити залежність від часу:
1. Модуля переміщення та побудувати графік \(\left| \Delta \vec{r}\left( t \right) \right|\) ;
2. Координат x(t), y(t);
3. Проєкцій швидкості vx(t), vy(t) і прискорення ax(t), ay(t) та обчислити їхні модулі.
|
Дано: R = 250 м
v = 10 м/с
\(\alpha=60^{\circ}\)
|
|
\(\left| \Delta \vec{r}(t)\right|\) - ?
x(t), y(t) - ?
vx(t), vy(t), v - ?
ax(t), ay(t), a - ?
|
Розв’язання
Умову задачі відображає рис. 26a.
1. Величину переміщення знайдемо за теоремою косинусів із трикутника AOC:
\(\left| \Delta \vec{r} \right|=\sqrt{{{R}^{2}}+{{R}^{2}}-2{{R}^{2}}\cos \varphi }=2R\cdot \left| \sin \frac{\varphi }{2} \right|\ .\)
Із геометрії відомо, що центральний кут φ = SR (рад), де S – довжина дуги кола між точками А і С, тобто пройдений шлях. Позаяк рух авто є рівномірним, то S = vt, і
|
\(\varphi =\frac{vt}{R}.\) |
(1) |
Тоді
\(\left| \Delta \vec{r} \right|=2R\left| \sin \left( \frac{vt}{2R} \right) \right|=500\left| \sin (0,02t) \right|.\)
Графік переміщення за час двох повних обертів руху 2T показано на рис. 26б.
2. З рис. 1.26а видно, що координати авто визначаються, як
\(x=R\cos \varphi ,\ \ y=R\sin \varphi \ .\)
Зробивши в цих виразах заміну (1), дістанемо:
|
\(x=R\cos \left( \frac{vt}{R} \right)=250\cos \left( 0,04t \right),\ \ \ \ \ y=R\sin \left( \frac{vt}{R} \right)=250\sin \left( 0,04t \right)\ .\) |
Звідси, відповідно до виразів (1.7а) і (1.7б), знайдемо:
\(v_{x}= x'(t)=-v\sin \left( \frac{vt}{R} \right)=-10\sin \left( 0,04t \right)\ ;\)
\(v_{y}= y'(t)=-v\cos \left( \frac{vt}{R} \right)=10\cos \left( 0,04t \right)\ .\)
3. Проєкції вектора прискорення визначаються аналогічно з виразів (1.7) і (1.8) :
\(a_{x}= v{{'}_{\text{x}}}=x''(t)=-v\sin \left( \frac{vt}{R} \right)=-0,4\cos \left( 0,04t \right)\ ;\)
\(a_{y}= v{{'}_{\text{y}}}=y''(t)=v\cos \left( \frac{vt}{R} \right)=-0,4\sin \left( 0,04t \right)\ .\)
Модуль прискорення
|
\(a=\sqrt{a_{\text{x}}^{2}+a_{\text{y}}^{2}}=\frac{{{v}^{2}}}{R}\) = 0,4 м/с2. |
Зауважимо, що отриманий результат є цілком передбачуваним – адже при рівномірному русі по колу прискорення тіла є доцентровим і визначається формулою (1.28).
| Задача 1.26 |
| Задача 1.27 |
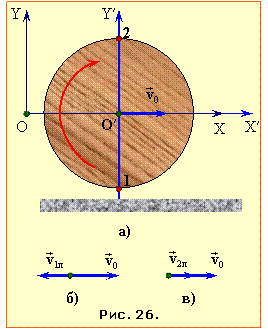 Диск рівномірно обертається навколо своєї осі, котра рухається горизонтально зі сталою швидкістю v0 = 2 м/с, рис. 26а.
Диск рівномірно обертається навколо своєї осі, котра рухається горизонтально зі сталою швидкістю v0 = 2 м/с, рис. 26а.
Визначити
швидкість v2 заданої точки 2 диска, якщо швидкість точки 1 дорівнює v1 =1м/с.
|
Дано: v1 = 1 м/с
v0 = 2 м/с
|
|
v2 - ?
|
Розв’язання:
Точки диска обертаються навколо осі й рухаються разом з нею. Тож для аналізу їхнього руху крім нерухомої системи відліку ХОY (рис. 1.27а), введемо й зв'язану з віссю диска рухому систему відліку X'O'Y', що має відносно нерухомої швидкість v0 і в якій швидкості точок диска ${\vec{v}}'$ є лінійними швидкостями їхнього обертального руху (див. п. 1.5). Тож за законом додавання швидкостей (1.10) для будь-якої точки диска можна записати:
|
$\vec{v}$ = ${\vec{v}}'$ + ${{\vec{v}}_{0}}$ $\Rightarrow $ ${{v}_{x}}={{{v}'}_{x}}+{{v}_{0}}$ |
(1) |
За умовою швидкість т. 1 в нерухомій системі відліку v1 < v0, що означає, що вектор ${{\vec{{v}'}}_{1}}$ є антипаралельним до \(\vec{v}_{0}\) (рис. 26б). Отже, диск обертається за годинниковою стрілкою, і в точці 2 вектори${{\vec{{v}'}}_{2}}$ і \({{\vec{v}}_{0}}\) є збіжні за напрямом (рис. 26в). Тому для проєкцій маємо: v0x = v0, ${{{v}'}_{1x}}$ = – v′, v2х = v2, і для кожної з точок формула (1) у проєкціях виглядає, як
\(v_{2}=v′+v_{0}\)
\(v_{1x}=-v′+v_{0}\)
Звідси випливає наступний результат:
|
\( {{v}_{2}}=-{{v}_{1x}}+2{{v}_{0}} .\) |
|
В умові задачі напрям руху точки 1 в нерухомій системі відліку ХОY не вказано. Тому, залежно від швидкості обертання диска і величини u, є можливі два випадки: 1) точка 1 відносно нерухомої системи відліку рухається праворуч, тоді v1x = v1, і 2) точка 1 рухається ліворуч, тож v1x = –v1. Тож задача має дві відповіді:
|
${{v}_{2}}=-{{v}_{1}}+2{{v}_{0}}$ = 3 м/с, і \({{v}_{2}}=v+2{{v}_{0}}=5\ \text{м/с}\ .\) |
| Задача 1.27 |
| Задача 1.28 |
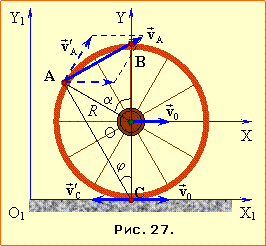 Колесо радіуса R котиться горизонтальною площиною без ковзання зі швидкістю \( {v}_{0}\).
Колесо радіуса R котиться горизонтальною площиною без ковзання зі швидкістю \( {v}_{0}\).
Визначити
швидкість v та прискорення а указаної точки на ободі, якщо її радіус обертання складає кут \( \alpha \) із вертикаллю.
|
Дано: \( {v}_{0}\) |
|
vА - ? а - ? |
Розв’язання
Пов'яжемо нерухому систему відліку XOY із площиною, а рухому X′O′Y′ – із віссю колеса, рис. 27. В такому разі швидкість осі колеса \( \vec{v}_{0}\) є швидкістю рухомої системи відліку, а лінійна швидкість обертання точки А навколо осі О′ \({{{\vec{v}}'}_{A}}\) – відносною швидкістю цієї точки. Тоді, згідно із законом додавання швидкостей (1.10), швидкість точки А відносно площини складає
\({{\vec{v}}_{A}}={{{\vec{v}}'}_{A}}+{{\vec{v}}_{0}}\).
Із паралелограма векторів на рис. 1.27, який відображає записану рівність, видно, що кут між векторами \( \vec{v}_{0}\) та \( \vec{v}_{A}^{\prime}\) дорівнює заданому кутові \( \alpha \). Тож за теоремою косинусів
\( {v}_{A}=\sqrt{(v^{\prime})^{2}+v_{0}^{2}+2v^{\prime}v_{0}\cos\alpha}\).
Позаяк кочення відбувається без ковзання, кожна точка колеса, що дотикається до площини, є відносно неї нерухомою:
\(\vec{v}_{с}=\vec{v}_{0}+\vec{v}_{с}^{\prime}\) = 0.
Отже,
\({{\vec{v}'}_{c}}\) = –\( \vec{v}_{0}\) \(\Rightarrow \) vс′ = v0.
Зрозуміло, що величина швидкості точки А є такою самою:
vА′ = v0.
Прискорення а′ точок колеса відносно його осі є доцентровим (формула (1.28)), отже на ободі його величина складає
\( {a}^{\prime}=\frac{v^{\prime{2}}}{R}=\frac{v_{0}^{2}}{R}\).
Відносно площини величина прискорення а така сама, позаяк вісь колеса відносно площини рухається без прискорення (див. п. 1.2).
| Задача 1.28 |
| Задача 1.29 |
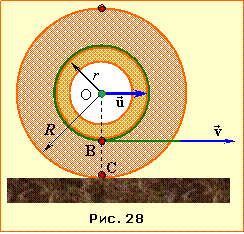 Котушка радіуса R із шаром ниток радіусом r лежить на шорсткій горизонтальній поверхні, рис. 28.
Котушка радіуса R із шаром ниток радіусом r лежить на шорсткій горизонтальній поверхні, рис. 28.
Визначити,
в якому напрямі і з якою швидкістю u покотиться котушка, якщо нитку горизонтально потягнути за вільний кінець із швидкістю \( {v}\).
|
Дано: R, r
\( {v}\)
|
|
\( {u}\) - ? |
Розв’язання
За умовою поверхня є шорсткою, тож котушка котитиметься по ній без ковзання. Це означає, що кожна точка котушки, що дотикається, на мить стає нерухомою відносно площини, ніби "пришпиленою" до неї. Тож при коченні без ковзання котушка в кожен момент часу лишень обертається навколо осі С, яка через це називається миттєвою віссю. При цьому очевидно, що напрям обертання котушки навколо миттєвої осі збігається із напрямом прикладеної до нитки сили. Отже, котушка буде рухатися праворуч, намотуючись на нитку (що без наведеного аналізу може здатися неочікуваним).
Швидкість \( {v}\), з якою тягнуть нитку, і шукана швидкість \( {u}\) осі О є лінійними швидкостями їхнього обертання навколо миттєвої осі С. Тому, позаяк кутова швидкість є однакова для усіх точок обертового тіла,то згідно з формулою (1.26) маємо:
\( \frac{v}{R-r}\) = \( \frac{u}{R}\) \(\Rightarrow \) \(u=\frac{R}{R-r}v\).
Наостанку зауважимо, що миттєва вісь існує не лише при коченні без ковзання, а й при деяких інших рухах тіл, що спрощує розв'язування відповідних задач механіки твердого тіла.
| Задача 1.29 |
| Задача 1.30 |
Із указаної точки на ободі колеса радіуса R, яке котиться горизонтальною площиною без ковзання, відлітає кусочок бруду.
Визначити
найменшу швидкість u колеса, при якій бруд знов потрапить у ту саму точку колеса при такому самому її розташуванні відносно осі.
|
Дано: R |
|
\( {u}\)-? |
Розв’язання
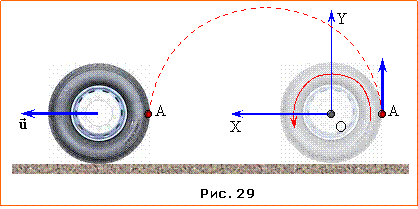 На рис. 29 показано початкове та кінцеве положення колеса, що задовольняє умову задачі. При цьому за час t між відривом і потраплянням бруду на колесо воно має здійснити щонайменше один повний оберт і пройти відстань \( {S}=2\pi{R}\). Отже, необхідна швидкість колеса складає
На рис. 29 показано початкове та кінцеве положення колеса, що задовольняє умову задачі. При цьому за час t між відривом і потраплянням бруду на колесо воно має здійснити щонайменше один повний оберт і пройти відстань \( {S}=2\pi{R}\). Отже, необхідна швидкість колеса складає
| \( {u}=\frac{2\pi{R}}{t}\). | (1) |
Для визначення часу t перейдемо в систему відліку колеса ХOY, в якій бруд відлітає й рухається далі вертикально із початковою величиною швидкості u та прискорення g . При цьому через половину часу польоту він опиняється в найвищій точці й має нульову миттєву швидкість. Отже,
\(u=\frac{gt}{2}\quad \Rightarrow \quad t=\frac{2u}{g}\).
Підставивши це значення t у вираз (1), отримаємо відповідь:
\(u=\frac{\pi Rп}{u}\) \( \Rightarrow \) \( u=\sqrt{\pi{gR}}\).
| Задача 1.30 |
| Задача 1.31 |
Два тягарці різної маси, що з'єднані ниткою, перекинутою через нерухомий блок радіуса R, спочатку утримують на одному рівні, а потім вивільнюють. Відтак вони без ковзання нитки за час τ = 1 с розійшлися на відстань nR один від одного.
Визначити
кут повороту блоку \( \varphi \) та набуте за цей час прискорення \( \vec{a}\) указаною точкою, якщо R = 10 см і n = 3.
|
Дано: R= 10 см n=3 t = 1 с, |
|
\(\varphi\) -? \(\vec{a}\) -? |
Розв’язання
За відсутності ковзання точки на ободі блоку та кожен із тягарців за вказаний час проходять однакові шляхи
|
$S=\frac{nR}{2}.$ |
(1) |
Отже, кут повороту блоку складає
|
\( \varphi=\frac{S}{R}=\frac{n}{2}\) (рад) = 86°. |
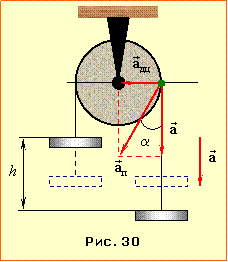 Далі визначаємо прискорення \(\vec{a}\) точок на ободі. Через різну вагу, тягарці рухаються прискорено, тож точки блоку змінюють не лише напрям, а й величину швидкості. Через це вони, крім доцентрового прискорення \({{\vec{a}}_{дц}}\) (див. п. 1.5), мають лінійне прискорення \({{\vec{a}}_{л}}\), котре показує, як швидко розганяється блок. Воно визначається приростом величини швидкості точки за одиницю часу і спрямоване по дотичній до блоку, як показано на рис. 30, і збігається з прискоренням тягарців.
Далі визначаємо прискорення \(\vec{a}\) точок на ободі. Через різну вагу, тягарці рухаються прискорено, тож точки блоку змінюють не лише напрям, а й величину швидкості. Через це вони, крім доцентрового прискорення \({{\vec{a}}_{дц}}\) (див. п. 1.5), мають лінійне прискорення \({{\vec{a}}_{л}}\), котре показує, як швидко розганяється блок. Воно визначається приростом величини швидкості точки за одиницю часу і спрямоване по дотичній до блоку, як показано на рис. 30, і збігається з прискоренням тягарців.
Таким чином, зміна вектора швидкості точок блоку визначається вектором повного прискорення
|
$\vec{a}={{\vec{a}}_{\text{л}}}+{{\vec{a}}_{\text{дц}}}$. |
Його модуль дорівнює
|
$ {a}=\sqrt{a_{дц}^{2}+a_{л}^{2}} $, |
(2) |
а напрям складає з ниткою кут α, що визначається співвідношенням:
|
$ \mathrm{tg}{\alpha}=\frac{a_{дц}}{{a}_{л}}$. |
(3) |
За відсутності ковзання нитки лінійне прискорення та швидкість точки на ободі блоку збігаються з прискоренням і швидкістю тягарців, які визначаються рівняннями кінематики (п. 1.3). Зокрема, враховуючи вираз (1), з рівняння (1.16) знаходимо:
| $ {{a}_{л}}=\frac{nR}{t^{2}}$. | (4) |
Далі з рівняння швидкості (1.16) визначаємо кінцеву швидкість тягарця
v = aлt = $ \frac{nR}{t}$
та за формулою (1.28) – величину доцентрового прискорення:
| aдц = \({{\left( \frac{nR}{t} \right)}^{2}}\cdot \frac{1}{R}\) = naл. | (5) |
Відтак за формулами (2), (4) і (5) знаходимо модуль вектора повного прискорення:
${{a}_{\text{л}}}\sqrt{{{n}^{2}}+1}$ = $\frac{R}{{{t}^{2}}}n\sqrt{{{n}^{2}}+1}$,
і за формулою (3) – його напрям:
α = arctg(n).
Обчислення дають:
а = 0,95 м/с2, α = 71,6°.