ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв’язування задач
Гідростатичний тиск. Сполучені посудини. Гідравлічні механізми
Задача 6.1. Циліндричне й два конічні відра однакового об'єму й висоти є вщент заповнені водою заданої маси m. Визначити силу тиску води на дно кожного відра, якщо радіуси отвору та основи в конічних відрах відрізняються вдвічі.
Задача 6.2. Визначити глибину h водойми, якщо тиск на невелике тіло на дні є в k = 3 рази більший ніж на поверхні. Атмосферний тиск P0 = 100 кПа, густина води ρ = 1 г/см3.
Задача 6.3. Довгу запаяну з одного боку й відкачану скляну трубку занурили відкритим кінцем у посудину зі ртуттю під кутом $\alpha=30{}^\circ$ до вертикалі. Визначити довжину l стовпчика ртуті в трубці при атмосферному тиску Р0 = 750 мм. рт. ст.
Задача 6.4. Кубічний акваріум об'ємом 150 л ущент заповнено водою (ρ = 1 г/см3). Визначити силу гідростатичного тиску на стінку акваріума.
Задача 6.5. Циліндри гідравлічного підйомника (див. п. 6.1) площею перерізу S1 = 1 м2 та S2 =25 см2 заповнено технічною олією (ρ = 0,8 г/см3). Нехтуючи вагою поршнів і тертям, визначити висоту h2, на яку підніметься малий поршень, якщо на платформу (великий поршень) покласти вантаж масою m = 200 кг.
Задача 6.6. В одне коліно сполучених посудин із ртуттю (ρр = 13,6 г/см3) наливають шар машинної олії (ρ0 = 0,75 г/см3) товщиною h0 = 40 см, а в інше – воду (ρв = 1 г/см3) до рівня олії. Визначити товщину шару води hв.
Задача 6.7. Для заміни колеса автівку масою 1 т її хочуть підважити за передній бампер гідравлічним домкратом із відношенням площ поршнів (S/S1) = 250 і ККД η = 80%. Визначити, яку силу для цього треба прикладати до малого поршня, якщо відстань від переднього бампера до центра ваги автівки складає п'яту частину його відстані до задньої осі.
Задача 6.1.
Циліндричне й два конічні відра однакового об'єму й висоти є вщент заповнені водою заданої маси m.
Визначити
силу тиску води на дно кожного відра, якщо радіуси отвору та основи в конічних відрах відрізняються вдвічі.
|
Дано: m R2 = 2R1 |
|
F0, F1 F2 - ? |
Розв’язання
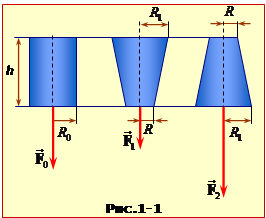
Профілі та розміри відер показано на рис. 1-1.
Сила гідростатичного тиску (6.2) на дно кожного відра визначається, як
| F = ρghS = πρghR2 |
(1) |
Для циліндричного відра величина hS = V – об'єм налитої води, отже, сила тиску на дно дорівнює її вазі:
| F = mg. |
|
У конічних відрах сили тиску на дно теж визначаються формулою (1):
| F1 = πρghR12; F2 = πρghR22. |
|
Тож вони є не однаковими й відрізняються від ваги води так, що
| ${{F}_{1}}=mg\frac{R_{1}^{2}}{{{R}^{2}}};\quad {{F}_{2}}=mg\frac{R_{2}^{2}}{{{R}^{2}}}$ |
|
Тому, врахувавши, що висота та місткість відер за умовою є однакові й R2 = 2R1, за формулами об'єму циліндра $V=h\pi R_{0}^{2}$ та зрізаного конуса \( {V}=\frac{1}{3}\text{ }\!\!\pi\!\!\text{ }h \left( {{R}^{2}}+R_{1}^{2}+R{{R}_{1}} \right) \) після елементарних викладок (зробіть самостійно!) знайдемо наступні значення шуканих сил:
${{F}_{1}}=\frac{3}{7}mg;\quad {{F}_{2}}=\frac{12}{7}mg$.
Як видно, сила тиску на дно в розширеному догори відрі є менша, а в звуженому – більша, ніж вага налитої води. Останній ефект, який називають "гідростатичним парадоксом", 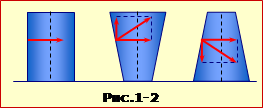
може здатися дивним, але має просте пояснення. Справа в тому, що вода у відрі взаємодіє не лише із дном, а й зі стінкою, причому сили тиску скрізь діють по нормалі до поверхні (рис. 1-2). Тож у циліндричному відрі вони є горизонтальними й не впливають на силу тиску на дно. В конічному відрі з розширеним верхом бічні сили спрямовані під деяким кутом до горизонту вгору і частково компенсують силу притягання mg води до землі, тим самим зменшуючи силу тиску на дно. А ось у звуженому догори відрі бічні сили, навпаки, створюють додатковий тиск на дно, що й пояснює гідростатичний парадокс.
Задача 6.2.
Визначити,
на якій глибині h в озері тиск, який діє на занурене тіло, буде у k = 3 рази більший за тиск на поверхні. Атмосферний тиск P0 = 100 кПа, густина води ρ = 1 г/см3.
|
Дано: k = 3
P0 = 100 кПа
ρ = 1 г/см3
|
|
h - ? |
Розв’язання
Тиск на тіло, що занурене в рідину з відкритою поверхнею, складається з атмосферного тиску P0 та гідростатичного тиску (6.2) на глибині занурення:
P = P0 + ρgh.
За умовою задачі P = kP0, отже,
Задача 6.3. Довгу запаяну з одного боку й відкачану скляну трубку занурили відкритим кінцем у посудину зі ртуттю під кутом $\alpha=30{}^\circ$ до вертикалі .
Визначити
довжину l стовпчика ртуті в трубці при атмосферному тиску Р0 = 750 мм.рт.ст.
|
Дано: α =30°
Р0 = 750 мм.рт.ст.
|
|
l - ? |
Розв’язання
 Історично склалося так, що на практиці атмосферний тиск вимірюють не в паскалях (Па), а в позасистемних одиницях – міліметрах ртутного стовпа, причому за означенням 1 мм.рт.ст. дорівнює гідростатичному тискові стовпчика ртуті висотою 1 мм.
Історично склалося так, що на практиці атмосферний тиск вимірюють не в паскалях (Па), а в позасистемних одиницях – міліметрах ртутного стовпа, причому за означенням 1 мм.рт.ст. дорівнює гідростатичному тискові стовпчика ртуті висотою 1 мм.
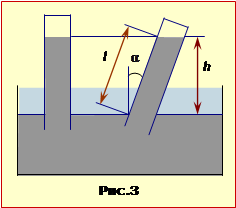
При зануренні ртуть у трубці під дією атмосферного тиску підніметься над рівнем у посудині на висоту h (див. рис. 3), при якій гідростатичний тиск (6.2) стовпчика зрівняється з атмосферним. Отже, за умовою, h = 750 мм. Тож очевидно, що шукана довжина стовпчика ртуті
$ {l}=\frac{h}{\cos \text{ }\!\!\alpha\!\!\text{ }} $ = 86,6 см.
Задача 6.4. Кубічний акваріум об'ємом 150 л ущент заповнено водою (ρ = 1 г/см3).
Визначити
силу гідростатичного тиску на стінку акваріума.
|
m = 150 кг |
|
F - ? |
Розв’язання
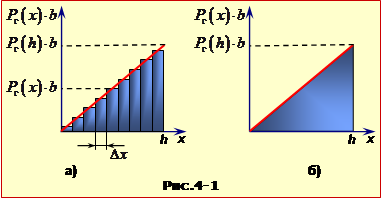
Якщо позначити ребро куба як а, то за формулою (6.2) тиск води на стінку при переміщенні вглиб лінійно зростає від нуля на поверхні до величини Р = ρga на дні, як показано на рис. 4-1. Тому для підрахунку сили тиску води на всю стінку подумки розділимо її на вузькі горизонтальні смужки шириною Δhi і площею ΔSi = а·Δhі, одну з яких показано на рис. 4-1. Тоді тиск Pi і сила тиску ΔFi на стінку в межах смужки
Pi ≈ ρghі, ΔFi ≈ Pi·ΔSi = аPiΔhі.
Відповідно, сила тиску на всю стінку
| $F\approx a\sum{{{P}_{i}}\Delta {{h}_{i}}}$ = aS |
(1) |
Записаний вираз є наближеним, бо в межах кожної смужки тиск на різних рівнях все ж не є однаковим. Але, якщо смужки поступово звужувати, вказана похибка буде зменшуватись, і в границі взагалі зникне. При цьому ''сходинки'' на графіку зіллються у відрізок прямої, й величина S у виразі (1) стане чисельно рівною площі трикутника, утвореного графіком P(h):
$S=\frac{1}{2}P(a)\cdot a$.
Отже, сила тиску води на стінку акваріума дорівнює
$F=\frac{1}{2}\rho g{{a}^{3}}$ $\Rightarrow $ ${F=\frac{mg}{2}}$.
У числах
F = 750 Н.
На завершення варто зауважити наступне. Сила тиску на кожну з чотирьох стінок складає (mg/2) – половину ваги всієї води. Тож може виникнути думка, що сила тиску на 4 стінки дорівнює 2mg, тобто вдвічі перевищує вагу всієї налитої води. Але такий "парадокс" є фейком, бо сума модулів векторів різного напрямку не дорівнює модулю їхньої суми. Тож насправді величина (модуль) сумарної сили тиску води на стінки акваріума дорівнює нулю.
Задача 6.5
Циліндри гідравлічного підйомника (див. п. 6.1) площею перерізу S1 = 1 м2 та S2 =25 см2 заповнено технічною олією (ρ = 0,8 г/см3). Нехтуючи вагою поршнів і тертям,
визначити
висоту h2, на яку підніметься малий поршень, якщо на платформу (великий поршень) покласти вантаж масою m = 200 кг.
|
Дано: S1 = 1 м2
S2 = 25 см2
m = 200 кг
ρ = 0,8 г/см3 |
|
h2 - ? |
Розв’язання
Рівноважне положення невагомих поршнів визначається рівністю тисків на основи циліндрів, які створюються атмосферою, стовпами рідини та покладеним вантажем. Але про атмосферний тиск не має сенсу говорити, бо він однаково діє на обидва поршні.
Згідно з виразом (6.2), платформа й малий поршень спочатку розташовуються на одному рівні, рис. 5а. Але після вміщення вантажу (рис. 5б) платформа опускається на певну відстань h1, а поршень піднімається на відповідну відстань h2, доки створювані вантажем і надлишковим стовпом води тиски P1 = (mg/S1) і P2 = ρg(h1+h2) не зрівняються.
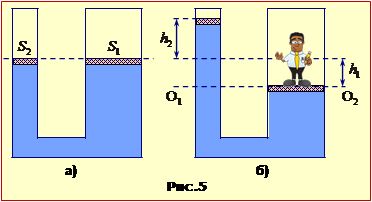 |
Отже,
|
\(\frac{m}{{{S}_{1}}}=\text{ }\!\!\rho\!\!\text{ }\left( {{h}_{1}}+{{h}_{2}} \right).\) |
(1) |
При цьому зміна об'ємів рідини в циліндрах є однакова, тож
|
\({{S}_{1}}{{h}_{1}}={{S}_{2}}{{h}_{2}}\) $\Rightarrow \quad {{h}_{1}}=\frac{{{S}_{2}}}{{{S}_{1}}}{{h}_{2}}$. |
(2) |
Підставивши отриманий вираз h1 у рівняння (1), після елементарних перетворень знайдемо наступну точну відповідь:
|
|
${{h}_{2}}=\frac{m}{{\rho }{\left( {{S}_{1}}+{{S}_{2}} \right)}}$. |
|
Але, позаяк за умовою величина S2 складає всього 0,25% від S1, відповідь можна без утрати точності записати більш лаконічно:
${{h}_{2}}=\frac{m}{\rho {{S}_{1}}}=25\text{см}$.
|
|
Задача 6.6. В одне коліно сполучених посудин із ртуттю (ρр = 13,6 г/см3) наливають шар машинної олії (ρ0 = 0,75 г/см3) товщиною h0 = 40 см, а в інше – воду (ρв = 1 г/см3) до рівня олії.
Визначити
товщину шару води hв.
|
Дано: h0 = 40 см
ρ0 = 0,75 г/см3
ρв = 1,0 г/см3
ρр = 13,6 г/см3
|
|
hв - ? |
Розв’язання
Оскільки \(\rho_{в}>\rho_{o}\), то межа поділу ртуті з водою O1- O2 проходить нижче, ніж для ртуті з олією, рис. 6-1.
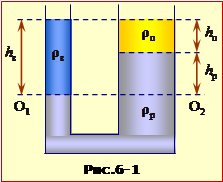 |
Тож, позаяк гідростатичний тиск (6.2) стовпа води висотою hв зрівноважується сумарним тиском стовпів олії (h0) та витісненої ртуті (hр), маємо:
ρвhв = ρ0h0 + ρрhр.
Відтак, зробивши очевидну заміну hр = hв – h0, отримаємо відповідь:
\({{h}_{\text{в}}}=40,8\ \text{см}.\)
Для заміни колеса автівку масою m = 1 т її хочуть підважити за передній бампер гідравлічним домкратом із відношенням площ поршнів (S/S1) = 250 і ККД η = 80%.
яку силу F1 для цього треба прикладати до малого поршня, якщо відстань l1 від переднього бампера до центра ваги автівки складає п'яту частину його відстані l до задньої осі.
|
Дано: m = 1 т l1 = 0,2 l |
|
F1 - ? |
Розв'язання
Для відриву передніх коліс автівки від землі (підважування), прикладена до бампера сила F має створювати відносно задньої осі (точніше – точок дотику коліс до землі) момент М1 = F1′l, який здатен подолати момент сили тяжіння М2 = mg(l–l1), див. рис. 6.7. За умовою М1 = М2, і
${{F}}=\frac{l-{{l}_{1}}}{l}mg=0,8mg$.
У такому разі шукана сила, згідно із співвідношення (6.4), мала би складати F1′ = (S1/S)F. Але через утрати енергії, які відображує ККД домкрата, реально до малого поршня треба прикласти силу F1 = F1′/η. Отже,
${{F}_{1}}=\frac{0,8mg}{\eta \left( {S}/{{{S}_{1}}}\; \right)}=40$ Н