physics.zfftt.kpi.ua

Задача 5.17. Дві маленькі кульки масами m₁ = 100 г та m₂ = 60 г з'єднані між собою тонким стрижнем масою m = 40 г і довжиною l = 20 см. Визначити,  на якій відстані Х_с від першої кульки знаходиться центр ваги системи.

Задача 5.18. Довести, що центр ваги трикутної пластини знаходиться на перетині медіан.

Задача 5.19. Визначити положення  центра ваги пластини заданої (рис. 5. 18) конфігурації та розмірів.

Задача 5.20. В однорідній квадратній пластинці зі стороною a = 1 м зроблено отвір радіуса r = (a/4), як показано на рис. 5. 19. Визначити, на якій відстані R від центра квадрата знаходиться центр ваги пластинки.

Задача 5.17

Дві маленькі кульки масами m₁ = 100 г та m₂ = 60 г з'єднані між собою тонким стрижнем масою m = 40 г і довжиною l = 20 см. 

Визначити, 

на якій відстані Х_с від першої кульки знаходиться центр ваги системи.

Розв’язання

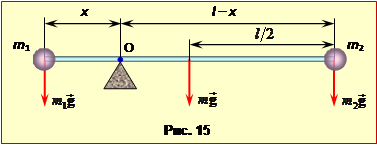
Якщо стрижень підперти в центрі ваги системи О,  (рис. 15), то система буде зрівноважена, тобто алгебраїчна сума моментів сил тяжіння \( {m}_{1}\vec{g}\), \( {m}_{2}\vec{g}\) і \( {m}\vec{g}\) відносно осі O дорівнюватиме нулю. Плечі цих сил показані на рис. 15 (враховано, що центр ваги стрижня знаходиться посередині). Отже маємо:

${{m}_{1}}g{{XR}_{c}}-mg\frac{l}{2}-{{m}_{2}}g\left( l-{{X}_{c}} \right)=0$,

звідки

X_c = $\frac{{{m}_{2}}+\left( {m}/{2}\; \right)}{m+{{m}_{1}}+{{m}_{2}}}l$ = 8 см.

Варто зауважити, що цей результат можна було б отримати одразу за загальною формулою (5.5а), підставивши задані маси m₁, m₂, m та координати кульок:  х₁ = 0,  х₂ = l – Х_с 0, х = (l/2).

Задача 5.18.

Довести,

що центр ваги трикутної пластини знаходиться на перетині медіан.

Розв’язання

Подумки розіб'ємо пластину на вузькі смужки паралельні до однієї із сторін трикутника. Очевидно, що центр ваги мужки знаходиться на її середині, а всього трикутника – на медіані даної сторони. Позаяк це стосується будь-якої зі сторін, то

центр ваги  трикутника є розташований на перетині його медіан.

Задача 5.19

Визначити 

координати центра ваги пластини заданої конфігурації та розмірів (рис. 16) .

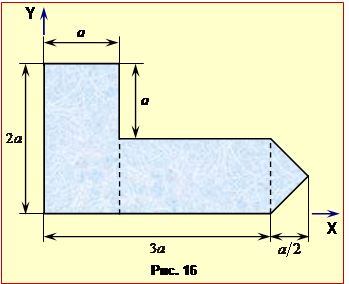
Розв’язання

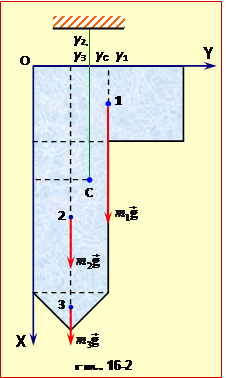
Жорстко зв'яжемо з пластиною систему координат XOY й подумки підвісимо її за удаваний центр ваги С один раз, як показано на рис. 16-1, а другий – як на рис.16-2. При цьому, позаяк в обох положеннях пластина є зрівноваженою, координати центра ваги можна знайти через рівняння моментів (5.4).

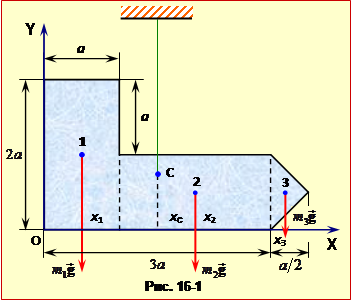
Для складання цих рівнянь поділимо пластину на два прямокутники 1, 2 та прямокутний трикутник 3, як показано штриховими лініями, і врахуємо, що центри ваги прямокутників знаходяться на перетині діагоналей, а трикутника – на перетині медіан. У такому разі при першій орієнтації для кожної частини пластини плече сили тяжіння відносно осі С через координати її центра ваги  x₁, x₂, x₃ та центра ваги всієї пластини X_c виражаються як h₁ =  X_c – x₁,   h₂ = x₂– X_c,  h₃  = x₃– X_c, відповідно. Відтак, приписавши в рівнянні (5.4) знак "+" моментам, які діють за годинниковою стрілкою, отримаємо:

\(-{{m}_{1}}\left( {{X}_{\text{c}}}-{{x}_{1}} \right)+{{m}_{2}}\left( {{x}_{2}}-{{X}_{\text{c}}} \right)+{{m}_{3}}\left( {{x}_{3}}-{{X}_{\text{c}}} \right)=0. \)

Звідси для координати центра ваги пластини  х_с маємо:

Координату Y_с центра ваги знайдемо, аналогічно визначивши плечі сил і записавши рівняння (5.4) для другої орієнтації пластини:

Варто зауважити, що формули (1) і (2) збігаються  з виразами (5.5а) і 5.5б) так, ніби кожен фрагмент пластини є матеріальною точкою відповідної маси, розміщеною в його центрі ваги.

Перейдемо до обчислень. Позначимо як m масу квадрата зі стороною a. Тоді, як зрозуміло з умови задачі, маси частин пластини складають

m₁ = m₂ = 2m,       m₃ = m/4.     

При цьому координати "х" точок 1, 2, 3  дорівнюють:

\( {{x}_{1}}=\frac{a}{2};\ \ \ \ \ \ \ {{x}_{2}}=2a;\ \ \ \ \ \ \ \ {{x}_{3}}=3a+\frac{a}{6}=\frac{19a}{6}\)

(враховано, що точка перетину медіан трикутника ділить їх відношення 1 : 2).

Аналогічно для координат "y" маємо:

\( {{y}_{1}}=a;\ \ \ \ \ \ \ {{y}_{2}}={{y}_{3}}=\frac{a}{2}. \)

Підставивши знайдені величини у формули (1) і (2), отримаємо відповідь:

\({{X}_{\text{c}}}=\frac{139a}{102}\approx 1,36a\)

і

\( {{Y}_{\text{c}}}=\frac{25a}{34}\approx 0,74a. \)

Задача 5.20

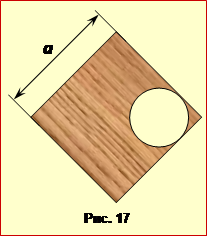В однорідній квадратній пластинці зі стороною a = 10 см (рис. 17) зробили отвір радіуса r =(a/4), як показано на .

Визначити,

на якій відстані Х від центра квадрата знаходиться центр ваги пластинки.

Розв’язання

Якщо подумки ''вставити на місце'' видалену частину, (рис.17-1), то утвориться суцільний квадрат, який при  підвішуванні в геометричному центрі O буде зрівноважений. Це означає, що сили тяжіння, котрі діють на пластинку з отвором \( {m}\vec{g}\) та на "вставку" \( {m}_{1}\vec{g}\),  відносно осі О створюють моменти однакової величини. Отже,

де Х_с = ОС – шукане плече сили тяжіння, що діє на пластинку з отвором,  а  l = ОС₁– плече сили тяжіння, що діє на "вставку".

Відношення мас і величина l легко знаходяться з рис. 5.19-1 і складають

$\frac{{{m}_{1}}}{m}$ = $\frac{{{S}_{1}}}{{{S}_{0}}-{{S}_{1}}}$ = $\frac{\pi }{16-\pi }$,

де  S₁ = π(a/4)² – площа отвору,  S₀ = a² – площа суцільного квадрата, та

l = $\frac{a\sqrt{2}}{4}$,

Відтак підставивши отримані величини у вираз (1), після обчислень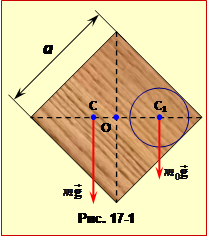

отримаємо відповідь:

R = 8,6 см.