ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс: Рівновага тіла, що не може обертатися

ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс

◄ Previous: Приклади розв'язування задач Next: Рівновага тіла з закріпленою віссю обертання ►

Приклади розв'язування задач

Рівновага тіла, що не може обертатися

Відповіді наведено для g = 10 м/с².

Задача 5.1. Вантаж маси M підвісили до стелі на канаті довжиною l і масою m. Визначити та показати на графіку залежність сили натягу каната Т від відстані x до точки кріплення вантажу.

Задача 5.2. Через два паралельні гладкі стрижні, що закріплені в одній горизонтальній площині на відстані 2l = 50 см, перекинуто нитку з двома тягарями однакової маси m₁ = m₂ = m, розташованими на одному рівні. Визначити: 1. На яку висоту h піднімуться тягарі, якщо посередині між стрижнями підвісити й повільно опустити до положення рівноваги гирю масою m₀ = km, де k = 1,2. 2. Чи буде ця рівновага стійкою?

Задача 5.3. Визначити, за якого мінімального коефіцієнта тертя μ клин із кутом α при забиванні в колоду не вислизатиме назад. Вагою клина знехтувати.

Задача 5.4. Дві невагомі пружини однакової довжини мають коефіцієнти жорсткості k₁ та k₂. Знайти жорсткість k складеної пружини, яка утвориться при з'єднанні цих пружин: 1) паралельно впритул і 2) послідовно.

Задача 5.5. Із двох однакових тонкостінних порожнистих півкуль радіуса R = 10 см, які щільно дотикаються одна до одної, відкачали повітря до тиску P = 80 кПа й підвісили їх до стелі так, аби лінія дотику була горизонтальна. Визначити найбільшу масу m тягаря, який можна підвісити до нижньої півкулі, аби вона не відірвалася при атмосферному тиску P₀ = 100 кПа. Товщиною стінок і масою півкуль знехтувати.

Задача 5.1.

Вантаж маси M підвісили до стелі на канаті довжиною l і масою m.

Визначити та показати на графіку

залежність T(x) сили натягу каната Т від відстані x від точки кріплення вантажу.

Дано:

M, m, l

T(x) - ?

Розв’язання

Натяг каната створюється не лише підвішеного вагою вантажу, а й вагою самого каната, що є рівномірно розподілена по його довжині. Тож у певній точці каната сила натягу дорівнює

T = (M + m′)g,

де m′ – маса частини каната між цією точкою та точкою кріплення вантажу, рис. 1а.

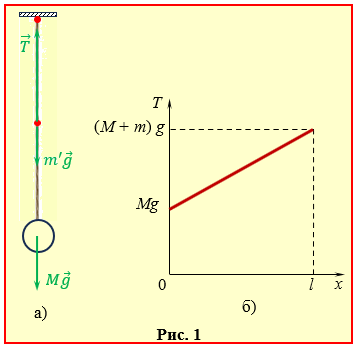
Очевидно, що

${m}'=m\frac{x}{l} $,

де m – маса всього каната, х – відстань від даної точки каната до точки кріплення вантажу.

Отже, відповідь задачі:

T(x) =$\left( M+m\frac{x}{l} \right)$g

(1)

Графік залежності T(x) наведено на рис. 1б.

Зауважимо, що при m = 0 сила натягу T = Mg не залежить від відстані х. Тож вираз (1) формально доводить положення, котре в задачах динаміки приймається по умовчанню: в невагомих нитках (мотузках, тощо) сила натягу є скрізь однакова.

Задача 5.2.

Через два паралельні гладкі стрижні, що закріплені в одній горизонтальній площині на відстані 2l = 50 см, перекинуто нитку з двома тягарями однакової маси m, розташованими на одному рівні.

Визначити

1. На яку висоту h піднімуться тягарі, якщо посередині між стрижнями підвісити й повільно опустити до положення рівноваги гирю масою m₀ = km, де k = 1,2.

2. Чи буде ця рівновага стійкою?

Дано:

2l = 50 см

m₀ = km

k = 1,2

h - ?

Розв’язання

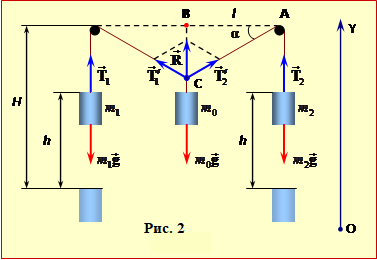
На рис. 2 схематично показано початкове та кінцеве положення тіл і сили, що діють на них.

Після підвішування в т А гиря опускається до т. А′, а тягарі підіймаються на шукану висоту h. При цьому відстань від точки кріплення гирі до кожного стрижня збільшується від заданого значення l до величини

${{l}_{1}}=\frac{l}{\cos \alpha }$.

Отже,

$h=l\left( \frac{1}{\cos \alpha }-1 \right)$

(1)

Таким чином, задача зводиться до визначення кута провисання нитки α, котрий залежить від співвідношення k мас гирі та тягарів. Величину α легко знайти з першої умови рівноваги твердого тіла (5.3), позаяк модулі всіх сил натягу однакові (для ниток, які утримують тягарі, це очевидно, а для тих, що утримують гирю, випливає з відсутності тертя в стрижнях):

${T}'={T}''=T$.

(2)

Справді, тягарі зрівноважуються натягом ниток

T = mg,

а гиря – рівнодійною $\vec{R}$ = ${\vec{T}}'$ + ${\vec{T}}''$, модуль якої складає (див. рис. 2)

$R=2T\sin \alpha $ = $2mg\sin \alpha $

(3)

і дорівнює m₀g. Отже, порівнюючи величини R і T, дістанемо

${{m}_{0}}=2m\sin \alpha $

і, врахувавши співвідношення m₀ = km, –

$\sin \alpha =\frac{k}{2}$ $\Rightarrow $ $\cos \alpha =\sqrt{1-{{\left( {k}/{2}\; \right)}^{2}}}$.

Відтак із виразу (1) отримаємо відповідь:

$ {h}=l\left(\frac{1}{\sqrt{1-{{\left( {k}/{2}\; \right)}^{2}}}}-1 \right)$ = 6,25 см.

Формальна відповідь на запитання, чи є рівновага стійкою, випливає з виразу (3). Дійсно, якщо гирю подумки трохи підняти (опустити) то сила R стане меншою (більшою) за m₀g, і після вивільнення гиря повернеться у вихідне положення. Отже, рівновага є стійкою.

На завершення з'ясуємо, чому в тексті наголошено на повільному опускання гирі. Справа в тому, що рівновага, або відсутність сил, які діють тіло, означає відсутність у нього прискорення, проте не швидкості. Тож, якщо після підвішування гирю просто відпустити, то, розігнавшись при вільному опусканні, вона за інерцією проскочить положення рівноваги, тож у момент зупинки величина R перевищуватиме m₀g. Відтак гиря почне прискорено підійматися, і все повториться у зворотньому порядку. Іншими словами, гиря буде здійснювати коливання, і поставлене в задачі запитання не матиме однозначної відповіді. Саме через це за умовою рух гирі не є вільним.

Задача 5.3.

Визначити,

за якого мінімального коефіцієнта тертя μ клин із кутом α при забиванні в колоду не вислизатиме назад. Вагою клина знехтувати.

Дано:

α = 30°

μ_min - ?

Розв’язання

На забитий в колоду клин діють сили нормальної реакції $ \vec{N}_{1}$, $ \vec{N}_{2}$, які виштовхують його, та сили тертя $ \vec{F}_{1}$, $ \vec{F}_{2}$, що утримують (рис. 2а). Очевидно, що клин не може обертатися, тож задля зручності будемо вважати, що всі сили є прикладені в одній точці (рис. 2б).

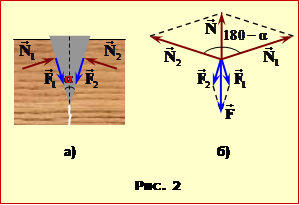Аби клин не вислизав, рівнодійні сил тиску $ \vec{N}=\vec{N}_{1}+\vec{N}_{2}$ та тертя $ \vec{F}=\vec{F}_{1}+\vec{F}_{2}$ мають бути зрівноважені:

$ \vec{N}+\vec{F}=0\ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ {F=N.}$

(1)

Із міркувань симетрії випливає, що $ {{N}_{1}}={{N}_{2}}$ і $ {{F}_{1}}={{F}_{2}}$. Тож (див. рис. 2б) умова рівноваги (1) набуває вигляду:

$ 2{{N}_{1}} \cos \left( 90{}^\circ -\frac{\alpha }{2} \right)$ = $2{{F}_{1}} \cos \frac{\alpha }{2}$ $\Rightarrow $ $\frac{{{F}_{1}}}{{{N}_{1}}}=\operatorname{tg}\frac{\alpha }{2}$

Звідси, позаяк сила тертя спокою ${{F}_{1}}\le \mu {{N}_{1}}$ (див. розділ 2, п. 2.4), отримуємо відповідь:

$ \mu\ge\mathrm{tg}\frac{\alpha }{2}$ $\Rightarrow $ μ_min = 0,27.

Задача 5.4.

Дві невагомі пружини однакової довжини мають коефіцієнти жорсткості k₁ та k₂.

Знайти

жорсткість k складеної пружини, яка утвориться при з'єднанні цих пружин: 1) паралельно впритул; 2) послідовно.

Дано:

k₁, k₂

k - ?

Розв’язання

Згідно із законом Гука (2.11) жорсткість пружини дорівнює відношенню прикладеної сили до видовження:

$k=\frac{F}{x}$.

(1)

У цьому й полягає задача.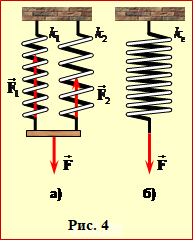

1) При навантаженні паралельно з'єднаних впритул пружин різної жорсткості (рис. 4a) перекосом перетинки можна нехтувати. В такому разі видовження кожної пружини збігається з видовженням системи: х₁ = х₂ = х, і за законом Гука (2.11) сили пружності в них складають:

$ {F}_{1}={k}_{1}x,\ \ \ {F}_{2}={k}_{2}x $.

Ці сили зрівноважують прикладену до системи силу F, отже,

$ {k}_{1}x\ + \ {k}_{2}x $ = $ {k}x $ $\Rightarrow $ $k={{k}_{1}}+{{k}_{2}}$

Одержана відповідь очевидно узагальнюється й на випадок паралельного з'єднання довільної кількості пружин:

$k=\sum{{{k}_{i}}}$

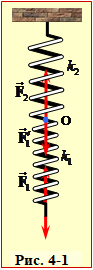
2) Розглянемо тепер умову рівноваги системи послідовно з'єднаних пружин, до якої прикладено силу $ \vec{F}$ (рис. 3-1). Безпосередньо вона прикладається до першої пружини і зрівноважується тільки силою $ \vec{F}_{1}$:

${{F}_{1}}=F.$

Відповідно, на нижній кінець другої пружини (точка О) безпосередньо діє лише перша пружина із силою ${{\vec{F}}_{1}}^{\prime }$, котра зрівноважується силою натягу другої пружини ${{\vec{F}}_{2}}$:Отже,

$F_{2}=F^{\prime}_{1}$.

Сили $ \vec{F}_{1}$ і $\vec{F}_{1}^{\prime}$ визначаються деформацією однієї пружини, тож

$F^{\prime}_{1}=F_{1}$.

Відтак із записаних рівностей випливає, що

$ {F}={{F}_{1}}={{F}_{2}}.$

(2)

Загальне видовження послідовно з'єднаних пружин дорівнює сумі видовжень кожної з них:

$ {x}={{x}_{1}}+{{x}_{2}}.$

Отже, згідно з виразом (1),

$\frac{F}{k}$ = $\frac{{{F}_{1}}}{{{k}_{1}}}+\frac{{{F}_{2}}}{{{k}_{2}}}=F\left( \frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}} \right)$,

і, враховуючи співвідношення (2), отримуємо:

$\frac{1}{k}=\frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}}$ $\Rightarrow $ $k=\frac{{{k}_{1}}{{k}_{2}}}{{{k}_{1}}+{{k}_{2}}}$

Для довільної кількості послідовно з'єднаних пружин розрахункова формула має наступний вигляд:

$ \frac{1}{k}=\sum\frac{1}{{{k}_{i}}}. $

Задача 5.5

Із двох однакових тонкостінних порожнистих півкуль радіуса R = 10 см, які щільно дотикаються одна до одної, відкачали повітря до тиску P = 80 кПа й підвісили їх до стелі так, аби лінія дотику була горизонтальна.

Визначити

найбільшу масу m тягаря, який можна підвісити до нижньої півкулі, щоби вона не відірвалася при атмосферному тиску P₀ = 100 кПа. Товщиною стінок і масою півкуль знехтувати.

Дано:

R = 10 см

P = 80 кПа

P₀= 100 кПа

m₀ - ?

Розв’язання

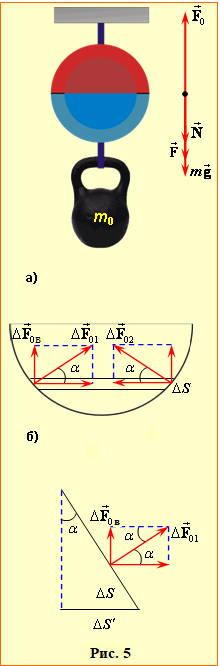
Невагома за умовою нижня півкуля утримується від падіння силою атмосферного тиску $\vec{F}_{0}$, яка долає вагу гирі $m\vec{g}$, силу залишкового тиску повітря всередині $\vec{F}$ і силу $\vec{N}$ (рис. 5а), з якою верхня півкуля діє на нижню. При цьому, за третім законом Ньютона (розділ ІІ, п. 2.2) з такою самою за величиною силою нижня півкуля притискається до верхньої. Тож, позаяк за умовою рівноваги

$\vec{F}_{0}$ + $m\vec{g}$ + $\vec{F}$ + $\vec{N}$ = 0,

сила, з якою півкулі притискаються одна до одної, дорівнює

N = F₀ – F – mg

(1)

Зрозуміло, що при збільшенні ваги тягаря притискання між півкулями буде зменшуватись і врешті зникне. Тож, шукану критичну масу тягаря m₀, котру можна розглядати як максимально допустиму при утриманні нижньої півкулі, або як мінімальну, необхідну для її відриву, знайдемо, поклавши в рівності (1) N= 0:

m₀g = F₀ – F

(2)

Далі визначимо величини F₀ і F, для чого на поверхні нижньої півкулі виділимо тонку горизонтальну смужку і подумки розчленуємо її на однакові малі діаметральні ділянки $ \Delta{S}$ (рис.7-1б). Тоді, позаяк сила тиску є перпендикулярна до поверхні, на кожну пару таких ділянок діють рівні за модулем сили $\vec{F}_{01}$ і $\vec{F}_{02}$, які лежать в одній вертикальній площині й зустрічно спрямовані під однаковими кутами $ \alpha $ до горизонту. Тож їхні горизонтальні складові є компенсовані, й рівнодійна напрямлена вертикально вгору. З таких парних ділянок складається вся смужка, а зі смужок – вся півкуля. Тому сила атмосферного тиску F₀, що діє на нижню півкулю, дорівнює сумі $ \Delta {{F}_{0B}}$ вертикальних складових сил тиску на кожну ділянку $ \Delta S $. Як видно з рис. 5б, їхня величина визначається, як

$\Delta {{F}_{B}}=\Delta {{F}_{0}}\sin \alpha $

а через атмосферний тиск P₀ – як

$\Delta {{F}_{B}}={{P}_{0}}\Delta S\sin \alpha ={{P}_{0}}\Delta {S}'$

де $ \Delta {S}'$ – площа проєкції ділянки $ \Delta{S}$ на горизонтальну площину. Отже, модуль сили атмосферного тиску на всю поверхню

$ {{F}_{0}}=\sum{{{F}_{0B}}={{P}_{0}}{S}',}$

де $ {S}'=\pi {{R}^{2}}$ – площа проєкції на горизонтальну площину всієї нижньої півсфери, котра являє собою круг радіуса R. Урахувавши це, маємо:

$ {{F}_{0}}=\pi {{R}^{2}}{{P}_{0}}. $

Аналогічно знаходимо й силу F залишкового тиску повітря всередині півкуль:

$ {F}=\pi {{R}^{2}}P. $

Відтак, підставивши отримані значення вирази F₀ і F у вираз (1), дістанемо відповідь:

$ {{m}_{0}}=\frac{({{P}_{0}}-{{P}_{1}})\pi {{R}^{2}}}{g}$ ≈ 63 кг.

◄ Previous: Приклади розв'язування задач Next: Рівновага тіла з закріпленою віссю обертання ►