ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс: Прямолінійний рух одного тіла та зв'язаних тіл

ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс

◄ Предыдущая: Приклади розв’язування задач Следующая: Зв'язок між імпульсом і силою ►

Приклади розв’язування задач

Прямолінійний рух одного тіла та зв'язаних тіл

Задача 2.1. Вантажівка рухається прямою дорогою зі швидкістю v₀ = 36 км/год. Визначити: а) відстань S від місця розвантаження, на якій водій має вимкнути двигун, аби вчасно зупинитися без використання гальм; б) час руху t до зупинки із вимкненим двигуном при коефіцієнті опору (відношенні сили опору до ваги авто) μ = 0,5.

Задача 2.2. На горизонтальному столі знаходяться зв'язані ниткою бруски масами m₁ і m₂. Визначити прискорення брусків a та сила натягу нитки T, якщо коефіцієнти тертя між ними та столом, відповідно, складають $ \mu_{1}$ і $ \mu_{2}$, і до першого прикладено горизонтальну силу F.

Задача 2.3. Горизонтальну дошку, на якій лежить шайба маси m, починають підіймати за один кінець. Визначити та побудувати графік залежності сили тертя F, що діє на шайбу, від кута нахилу дошки до горизонту α при заданому коефіцієнті тертя μ.

Задача 2.4. Підлогою тягнуть за мотузку ящик масою m = 100 кг, прикладаючи силу під кутом до горизонту. Коефіцієнт тертя між ящиком та підлогою μ = 0,5. Визначити найменшу силу ${{\vec{F}}_{\min }}$, якою можна рухати ящик.

Задача 2.5. Брусок знаходиться на похилій площині, кут нахилу якої до горизонту α можна змінювати за допомогою вертикального штока (упора). Знайти величину кута α₀, при якій брусок із стану спокою найшвидше спуститься від упора до основи при коефіцієнті тертя μ = 0,14.

Задача 2.6. Два тягарці масою M кожен, які зв'язані перекинутою через нерухомий блок ниткою, спочатку утримують на одному рівні. Потім до одного підвішують важок масою m і вивільняють систему. Визначити: а) прискорення a тягарців та час t, за який вони розійдуться на відстань H за відсутності ковзання нитки; б) силу натягу нитки $ {T}_{0}$, на якій підвішено важок, та силу тиску $ {F}$ на вісь блока.

Задача 2.7. На початку підйому та спуску ліфт має однакове прискорення. Визначити його величину a, якщо вага тіл у ліфті при підйомі в n = 1,5 рази перевищує вагу при спуску.

Задача 2.8. Повітряна куля загальною масою M = 1000 кг опускається зі сталою швидкістю. Визначити масу баласту m, яку треба скинути, аби куля почала підійматися з тою самою швидкістю. Піднімальна (архімедова) сила, що діє на кулю, F = 9700 H.

Задача 2.1

Задача 2.1

Вантажівка рухається прямою дорогою зі швидкістю v₀ = 36км/год.

Визначити:

а) відстань S від місця розвантаження, на якій водій має вимкнути двигун, аби вчасно зупинитися без використання гальм;

б) час руху t до зупинки із вимкненим двигуном при коефіцієнті опору (відношенні сили опору до ваги авто) μ = 0,5.

Дано:

v₀ = 36 км/год

$ \mu={0{,}5}$

S - ? t - ?

Розв'язання

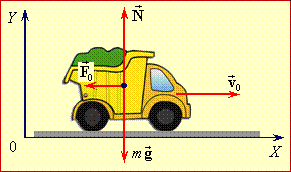
а) При вимкненому двигуні на вантажівку діють три сили: тяжіння $ {m}\vec{g}$, нормальна реакція опори $ \vec{N}$ та сила опору $ \vec{F}_{0}$ (рис. 2.1). Зрозуміло, що вертикальні сили є компенсовані:

$ {m}\vec{g}+\vec{N}$ = 0.

Отже,

$ {m}\vec{a}=\vec{F}_{0}$,

або у проекціях на напрям руху (вісь OX)

$ {m}a_{x}=-F_{0}$.

Знак мінус стоїть тому, що вектор $ \vec{a}$ є протилежним до напрямку руху. Сила опору визначається, як $ {F}_{0}=\mu{mg}$, отже

$ {a}_{x}=-\mu{g}$.

Відтак за формулою (1.19а) знаходимо шлях вантажівки до зупинки:

$ {S}=\frac{v_{0}^{2}}{2\mu{g}}$ ≈ 100 м.

б) Для визначення часу руху вантажівки до зупинки використаємо рівняння швидкості $ {v}_{x}$ (1.16), звідки з урахуванням знаків проєкцій отримуємо:

$ {v}_{0}-\mu{mgt}={0}$ $ \Rightarrow $ $ {t}=\frac{v_{0}}{\mu{g}} = 20{,}4$ c.

Величину t також можна знайти і з рівняння ІІ закону Ньютона (2.4), згідно з яким зміна імпульсу вантажівки $ \Delta{\vec{p}}=-m\vec{v}_{0}$ дорівнює імпульсові сили опору за час руху до зупинки $ \vec{F}_{0}{t}$. Позаяк ці вектори мають однаковий напрям, то

$ {mv}_{0}=F\Delta{t}$ $ \Rightarrow $ $ \Delta{t}=\frac{mv_{0}}{F}=\frac{mv_{0}}{\mu{mg}}=\frac{v_{0}}{\mu{g}}$,

що, природньо, збігається з раніше отриманим результатом.

Задача 2.3

Задача 2.2

На горизонтальному столі знаходяться зв'язані ниткою бруски масами m₁ і m₂.

Визначити

прискорення брусків a та сила натягу нитки T, якщо коефіцієнти тертя між ними та столом, відповідно, складають $ \mu_{1}$ і $ \mu_{2}$, і до першого прикладено горизонтальну силу F.

Дано:

m₁, m₂

μ₁, μ₂

a - ?

T - ?

Розв'язання

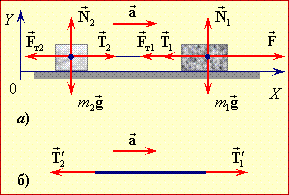
На бруски діють сили тяжіння $ {m}_{1}\vec{g}$, $ {m}_{2}\vec{g}$, реакції опори $ \vec{N}_{1}$, $ \vec{N}_{2}$, тертя $ \vec{F}_{т1}$, $ \vec{F}_{т2}$, прикладена сила $ \vec{F}$ та сили натягу нитки $ \vec{T}_{1}$ і $ \vec{T}_{2}$ = –$ \vec{T}_{1}$, рис. 2.2.

Позаяк прискорення тіл однакові, і сили тяжіння та реакції опори компенсовані, то рівняння руху (2.5) брусків мають вигляд:

$ \vec{F}+\vec{F}_{т1}+\vec{T}_{1}=m_{1}\vec{a}$,

$ \vec{T}_{2}+\vec{F}_{т2}=m_{2}\vec{a}$.

Для розрахунків перепишемо їх через проєкції векторів на напрям руху (вісь ОХ), врахувавши, що Т₁ = Т₂=Т, F_т1 = μ₁m₁g і F_т2 = μ₂m₂g:

F – μ₁m₁g – Т =m₁a,

Т – μ₂m₂g = m₂a.

(1)

Далі, додавши праві та ліві частини рівнянь (1), знайдемо прискорення брусків:

$ {F}-(\mu_{1}m_{1}+\mu_{2}m_{2})g=(m_{1}+m_{2}){a}$ $ \Rightarrow $

$ {a}=\frac{{F}-(\mu_{1}m_{1}+\mu_{2}m_{2})g}{m_{1}+m_{2}}$.

(2)

Відтак, підставивши вираз прискорення (2) у будь-яке з рівнянь (1), для сили натягу нитки отримаємо:

${T}=\frac{{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}\left[ F+\left( {{\mu }_{2}}-{{\mu }_{1}} \right){{m}_{1}}g \right] $.

Отже, сила натягу нитки, що з'єднує бруски, визначається різницею коефіцієнтів тертя. Тож μ₁ = μ₂ наявність тертя на неї взагалі не впливає.

Наостанку зауважимо, що вираз прискорення (2) за змістом є настільки очевидний, що його можна було би записати одразу. Але попередні міркування і викладки були наведені як ілюстрація загального алгоритму застосування другого закону Ньютона.

Задача 2.4

Задача 2.3

Горизонтальну дошку, на якій лежить шайба маси m, починають підіймати за один кінець.

Визначити та побудувати графік

залежності сили тертя F, що діє на шайбу, від кута нахилу дошки до горизонту α при заданому коефіцієнті тертя μ.

Дано

F(α)-?

Розв'язання

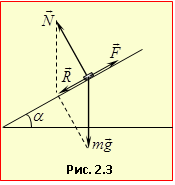
На шайбу діють сили: тяжіння $ {m}\vec{g}$ і нормальної реакції площини $ \vec{N}$ та тертя $ \vec{F}$. При порівняно невеликих кутах нахилу, поки не почалося ковзання тіла, $\vec{F}$ – це сила тертя спокою. Згідно з формулою (2.13) вона зрівноважує рівнодійну решти сил $\vec{R}=m\vec{g}+\vec{N}$ (рис. 2.3), модуль якої R = mgsinα. Отже, при невеликих $ \alpha $ сила тертя залежить від кутах нахилу площини за законом

$ {F}=mg\sin\alpha $.

(1)

При збільшенні кута $ \alpha $ сила тертя спокою F зростає і при певному куті $ \alpha_{0}$, який називають "кутом тертя", досягає максимально можливого значення μN (формула (2.14)). Сила N компенсує нормальну до площини складову сили тяжіння, тож максимальна сила тертя спокою F_m = μmgcosα₀. Відтак, враховуючи вираз (1), маємо:

mgsinα₀ = μmgcosα₀, → α₀= arctgμ.

При кутах нахилу площини α > α_0,коли шайба рухається, на неї діє сила тертя ковзання

${F}=\mu{mg}\cos\alpha $.

Таким чином, сила тертя між шайбою та площиною в залежності від кута нахилу площини виражається однією з формул: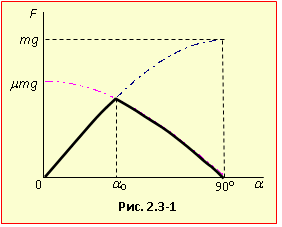

1. $ {F}=mg\sin\alpha $ при $ {0}\le\alpha\le\alpha_{0}$;

2. $ {F}=\mu{mg}\cos\alpha $ при $ \alpha_{0}<\alpha\le{90}^{\circ}$.

($ \alpha_{0}=\mathrm{arctg}\mu $).

Отже, графік $ {F}(\alpha) $, рис. 2.3-1, складається з відрізка синусоїди (1) і відрізка косинусоїди (2).

Задача 2.2

Задача 2.4

Підлогою тягнуть за мотузку ящик масою m = 100 кг, прикладаючи силу під кутом до горизонту. Коефіцієнт тертя між ящиком та підлогою μ = 0,5.

Визначити

найменшу силу ${{\vec{F}}_{\min }}$, якою можна рухати ящик.

Дано:

m = 100 кг

μ = 0,5

α_min - ?

F_min- ?

Розв'язання

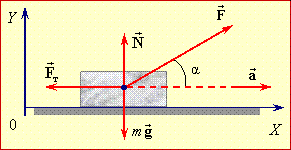
На ящик діють сили тяжіння $ {m\vec{g}}$, нормальної реакції опори $ \vec{N}$, тертя $ \vec{F}_{т}$ та натягу мотузки $ \vec{F}$, що дорівнює прикладеній силі (рис. 2.4).

За ІІ законом Ньютона (2.5) рівняння руху ящика має вигляд

$ \vec{F}+m\vec{g}+\vec{N}+\vec{F}_{\mathrm{т}}=m\vec{a}$.

Ящик рухається горизонтально (a_y = 0, a_x = a), тож у проекціях на осі координат маємо

OX: $ {F}\cos\alpha-F_{т}={ma}$,

OY: $ {F}\sin\alpha+N-mg={0}$.

Урахувавши, що сила тертя $ {F}_{\mathrm{т}}=\mu{N}$, отримуємо систему рівнянь

$\left\{ \begin{matrix} F\cos \alpha -\mu N=ma, \\ F\sin \alpha +N-mg=0 \\ \end{matrix} \right.$,

з якої знайдемо прикладену натягу мотузки, при якій ящик рухається із прискоренням а:

$ {F}=\frac{\mu{mg}+ma}{\cos\alpha+\mu\sin\alpha}$.

Її мінімальна величина, потрібна для руху ящика, відповідає умові a = 0 і складає

$ {F}_{0}=\frac{\mu{mg}}{\cos\alpha+\mu\sin\alpha}$.

(1)

З умови задачі випливає, що сила F при певному значенні кута α є найменшою, тобто тягти ящик найлегше. Чому це так, можна зрозуміти, проаналізувавши залежність F₀(α) при малих та при великих значеннях α. Справді, при малих кутах косинус є близький до одиниці і майже не змінюється при збільшенні кута, тоді як синус швидко зростає. Тому знаменника у виразі (1) зростає, а величина F₀ зменшується. При великих кутах все відбувається навпаки – косинус стрімко зменшується, тоді як синус майже не змінюється, і F₀ збільшується. Тож при певному значенні кута α = α_min знаменник у виразі (1)

$ {f}(\alpha)=\cos\alpha+\mu\sin\alpha $

(2)

буде максимальним, а необхідна для пересування ящика сила F₀ – мінімальною.

Для визначення величини α_min уведемо позначення $ \mu=\mathrm{tg}\varphi $. Тоді формула (2) набуває вигляду

$ f(\alpha)=\cos\alpha+\frac{\sin\varphi}{\cos\varphi}\sin\alpha=\frac{\cos{(\alpha-\varphi)}}{\cos\varphi}$.

Кут $ \varphi $ є незмінним, тож функція $ {f}(\alpha)$ досягає максимуму за умови $ \cos{(\alpha-\varphi)}={1}$, тобто при $ \alpha_{\mathrm{min}}=\varphi $. Отже натяг мотузки мінімальний при

$ \mathrm{tg}\alpha_{\mathrm{min}}=\mu$ $ \Rightarrow $ $ \alpha_{\mathrm{min}}=\mathrm{arctg}\mu $ = 26,6°.

(3)

Примітка. Якщо ви з математики вже знаєте похідні, відповідь можна знайти простіше, взявши та прирівнявши до нуля похідну функції (2):

$ {f}^{\prime}(\alpha)=-\sin\alpha+\mu\cos\alpha $ $ \Rightarrow $

$ -\sin\alpha_{\mathrm{min}}+\mu\cos\alpha_{\mathrm{min}}=0$,

звідки

$ \alpha_{\mathrm{min}}=\mathrm{arctg}\mu $.

що, збігається з (3).

Урахувавши отриманий для tgα вираз (3) і замінивши за відомими формулами cosα i sinα у виразі (1) через tgα, після елементарних спрощень отримаємо другу відповідь:

${{F}_{\min }}=\frac{\mu mg}{\sqrt{1+{{\mu }^{2}}}}$ ≈ 450 Н.

Задача 2.5

Задача 2.5

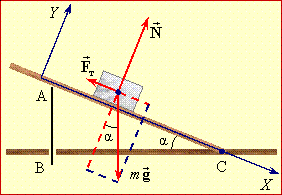
Брусок знаходиться на дошці із закріпленим кінцем, кут нахилу якої до горизонту α можна змінювати за допомогою вертикального упора (штока)на рис. 2.5.

Знайти,

при якій величині кута α₀ брусок із стану спокою найшвидше спуститься від упора до точки кріплення дошки при коефіцієнті тертя μ = 0,14.

Дано:

$ \mu={0{,}14}$

$ \alpha_{m}$-?

Розв'язання

Очевидно, що, аби отримати відповідь, спочатку треба встановити залежність t(α) часу спуску бруска від кута нахилу дошки.

Умову задачі ілюструє рис. 2.5. На брусок діють сили тяжіння $ {m\vec{g}}$, реакції опори $ \vec{N}$ та тертя $ \vec{F}_{т}$, отже, рівняння руху (2.5) має вигляд:

$ {m}\vec{g}+\vec{N}+\vec{F}_{т}=m\vec{a}$,

і в проєкціях на осі координат:

OX: $ {mg}\sin\alpha-F_{т}=ma $,

OY: $ {N}-mg\cos\alpha={0} $ $\Rightarrow $

$ {N}=mg\cos\alpha $

(1)

Відтак, урахувавши, що F_т = μN = μmgcosα, з першого рівняння системи (1) визначимо прискорення бруска

$ {a}=g(\sin\alpha-\mu\cos\alpha)$,

і, за рівнянням (1.16), час проходження рим відстані l між точками А і С:

$ {t}=\sqrt{\frac{2l}{g(\sin\alpha-\mu\cos\alpha)}}$.

(2)

Згідно з отриманим виразом, цей час руху бруска формально залежить від двох величин – α і l. Але l = l₀/cosα, де відстань між точками В і С l₀ = const. Тож величина t виражається, як

$t\left( \alpha \right)$ = $\sqrt{\frac{2{{l}_{0}}}{g\cos \alpha \left( \sin \alpha -\mu \cos \alpha \right)}}$,

і залежить тільки від кута α. Характер цієї залежності визначається поведінкою функції в знаменнику

$ {f}(\alpha)=\cos\alpha (\sin\alpha-\mu\cos\alpha )$,

(3)

котру не важко якісно проаналізувати так, як у попередній задачі. При малих кутах збільшення α спричинює зростання f(α) і зменшенням часу спуску. А в області великих кутів при збільшенні α функція f(α) спадає, і час спуску збільшується. Отже, при деякому куті α = α_m функція f(α) має максимум, і час спуску бруска є найменшим.

За канонами математики, щоби визначити величину α_m, треба знайти й прирівняти до нуля похідну f′(α):

$ {f}^{\prime}(\alpha)=-\sin\alpha (\sin\alpha-\mu\cos\alpha )+\cos\alpha (\cos\alpha+\mu\sin\alpha){=}$

$ {=}\sin^{2}\alpha+\cos^{2}\alpha+2\mu\sin\alpha\cos\alpha=\cos{2}\alpha+\mu\sin{2\alpha}$, отже,

$ \cos{2\alpha_{m}}+\mu\sin{2\alpha_{m}}={0}$, $\Rightarrow $ $\operatorname{tg}2\alpha =-\frac{1}{\mu }$.

Звідси при μ = 0,14 шуканий оптимальний кут нахилу площини до горизонту складає 41°.

Примітка. Безпосередньо з отриманого виразу виходить α_m = – 41°. Це пояснюється тим, що кут між віссю ОХ і напрямком руху бруска, котрий фігурує в рівняннях (1), є від'ємним.

Задача 2.7

Задача 2.6

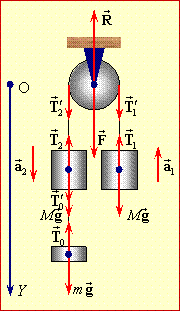
Два тягарці масою M кожен, зв'язані перекинутою через нерухомий блок ниткою, спочатку утримують на одному рівні. Потім до одного підвішують важок масою m і вивільняють систему.

Визначити:

а) прискорення a тягарців та час t, за який вони розійдуться на відстань H за відсутності ковзання нитки;

б) силу натягу нитки $ {T}_{0}$, на якій підвішено важок і силу тиску $ {F}$ на вісь блока.

Дано:

M, m

a - ?

t - ?

T - ?

F - ?

Розв'язання

Сили, що діють на кожне з тіл задачі, показані на рис. 2.6. Правий тягарець M взаємодіє з Землею (сила $ {M}\vec{g}$) та з ниткою (сила $ \vec{T}_{1}$). Так само на важок m діють сили $ {m}\vec{g}$ і $ \vec{T}_{0}$. Лівий тягарець M взаємодіє із Землею (сила $ {M}\vec{g}$) та двома нитками (сили $ \vec{T}_{2}^{\prime},\,\vec{T}_{0}^{\prime}$ ). На блок з боку ниток діють сили $ \vec{T}_{1}^{\prime},\,\vec{T}_{2}^{\prime}$. Ця дія передається на вісь блока, створюючи силу $ \vec{F}=\vec{T}_{1}^{\prime}+\vec{T}_{2}^{\prime}$.

а) Прискорення кожного з трьох тіл визначається ІІ законом Ньютона (2.5):

$ {M}\vec{g}+\vec{T}_{1}=M\vec{a}_{1}$,

$ M\vec{g}+\vec{T}_{0}+\vec{T}_{2}=M\vec{a}_{2}$,

(1)

$ {m}\vec{g}+\vec{T}_{0}=m\vec{a}_{2}$.

При цьому, позаяк блок є невагомий, і ковзання нитки відсутнє, прискорення і сили натягу кожної ниток однакові: $ {T}_{1}=T_{1}^{\prime}=T_{2}=T_{2}^{\prime}={T}$, $ {T}_{0}=T_{0}^{\prime}$ і $ {a}_{1}=a_{2}={a}$. Врахувавши це, запишемо рівняння (1) у проєкціях на напрямлену вертикально вниз вісь OY нерухому відносно осі блока :

$ {M}g-T=-M{a}$,

$ Mg+T_{0}-T=M{a}$,

(2)

$ mg-T_{0}=m{a}$.

Для визначення величини а додамо ліві та праві частини рівнянь (2), попередньо помноживши перше на (-1):

$ {mg}=(2M+m){a}$ $ \Rightarrow $ $ {a}=\frac{m}{2M+m}{g}$.

(3)

Тягарці рухаються в протилежних напрямках без початкової швидкості та з однаковим прискоренням а. Тож за шуканий час кожен пройде однаковий шлях $ {l}=H/2 $. Тому, згідно з рівняннями (1.16),

$ \frac{H}{2}=\frac{at^{2}}{2}$ $ \Rightarrow $ $ t=\sqrt{\frac{H}{a}}$.

Підставивши сюди вираз (3), отримуємо шуканий час:

$ {t}=\sqrt{\frac{2M+m}{m}\cdot\frac{H}{g}}$.

(4)

б) Силу натягу T₀ нитки, що з'єднує тягарець M із важком m, знайдемо з останнього рівняння (2), підставивши вираз (3):

$ {T}_{0}=m(g-a)=Mg\left(1+\frac{m}{2M+m}\right) $ $ \Rightarrow $ $ {T}_{0}=\frac{2Mg}{2M+m}{g} $.

Отже, сила тиску на вісь блока

$ {F}=T_{1}^{\prime}+T_{2}^{\prime}=2{T}$.

Величину T знайдемо з першого рівняння (2), підставивши вираз (3):

$ {T}=M(g+a)=Mg\left(1+\frac{m}{2M+m}\right) $ $ \Rightarrow $ $ {T}=\frac{2M(M+m)}{2M+m}{g}$.

Таким чином, шукана сила тиску на вісь блока дорівнює

$ {F}=\frac{4M(M+m)}{2M+m}{g}$.

Задача 2.8

Задача 2.7

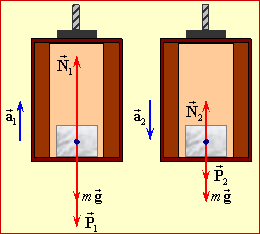
На початку підйому та спуску ліфт має однакове прискорення.

Визначити

його величину a, якщо вага тіл у ліфті при підйомі в n = 1,5 рази перевищує вагу при спуску.

Дано:

n = 1,5

a - ?

Розв'язання

На тіло діють сила тяжіння $ {m}\vec{g}$ та нормальна реакція опори (підлоги ліфта) $ \vec{N}$ (рис. 2.7). За означенням вага тіла $ \vec{P}$ – то є сила, з якою воно діє на підлогу ліфта. Отже, за третім законом Ньютона

$ \vec{P}=-\vec{N}$.

(1)

Згідно з другим законом Ньютона (2.5), для кожного випадку маємо:

	$ \vec{N}_{1}+m\vec{g}=m\vec{a}_{1}$,	(2)
	$ \vec{N}_{2}+m\vec{g}=m\vec{a}_{2}$.	(2)

Переписавши рівняння (2) у проекціях на напрям руху ліфта і врахувавши, що $ {a}_{1}=a_{2}={a}$, і P = N, отримаємо:

$ {P}_{1}=m(g+a)$ $ {P}_{2}=m(g-a)$ $ \Rightarrow $ $ \frac{P_{1}}{P_{2}}=\frac{g+a}{g-a}$.

Звідси, згідно з умовою $ \frac{P_{1}}{P_{2}}={n}$, дістанемо відповідь:

$ \frac{g+a}{g-a}={n}$ $ \Rightarrow $ \( {a}=\frac{n-1}{n+1}g= 2 м/с².

Задача 2.9

Задача 2.8

Повітряна куля загальною масою M = 1000 кг опускається зі сталою швидкістю.

Визначити

масу баласту m, який треба скинути, аби куля почала підійматися з такою самою швидкістю, якщо архімедова сила, що діє на кулю, F = 9700 H.

Дано:

M = 1000 кг

F = 9800 Н

m -?

Розв'язання

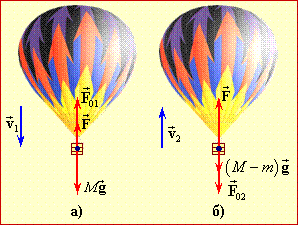
За умовою, попри те, що сила тяжіння $M\vec{g}$ та архімедова сила $\vec{F}$, що діють на кулю, не однакові, підйом є рівномірним. Отже, їхня різниця компенсується силою опору повітря ${{\vec{F}}_{01}}$, рис. 2.8а. Це стосується й сили опору ${{\vec{F}}_{02}}$ (рис. 2.8б), що діє на кулю після скидання баласту. При цьому, через рівність швидкостей підйому та спуску, сили опору за величиною теж однакові: ${F}_{01}$ = ${F}_{02}$. Піднімальну силу \){F}$ теж можна вважати однаковою, позаяк об'єм викинутог о баласту є набагато менший за об'єм кулі. Різняться тільки сили тяжіння: \(M\vec{g}$ при опусканні та \){(M-m)}\vec{g}$$ при підйомі. При цьому в обох випадках прискорення відсутнє, отже сили є компенсовані:

$\left\{ \begin{align} & Mg\quad \quad \ \ =F+{{F}_{0}} \\ & Mg-mg=F-{{F}_{0}} \\\end{align} \right.$.

Звідси після додавання лівих і правих частини рівнянь знайдемо відповідь:

$m=\frac{2\left( Mg-F \right)}{g}=60\text{ }\text{кг.}$

◄ Предыдущая: Приклади розв’язування задач Следующая: Зв'язок між імпульсом і силою ►

	\( \vec{N}_{1}+m\vec{g}=m\vec{a}_{1}\),	(2)
	\( \vec{N}_{2}+m\vec{g}=m\vec{a}_{2}\).	(2)