ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
2. Приклади розв'язування задач
2.2. Прямолінійний рівнозмінний рух одного тіла
Задача 1.9. Літак рухається прямолінійно спочатку зі швидкістю \(v_{0}\) = 720 км/год, а потім протягом t = 10 с рівно-прискорено так, що за останню секунду (проміжок часу \( \tau \) ) долає відстань S = 295 м. Визначити кінцеву швидкість літака \( {v}\).
Задача 1.10. Потяг, який рухається прямолінійно рівно-прискорено, на певній ділянці шляху збільшує швидкість на \( \Delta{v} \) = 60 км/год при середній швидкості \( \langle{v}\rangle \) = 40 км/год. Визначити швидкість поїзда \( {v}\) посередині згаданої ділянки.
Задача 1.11. Тіло вільно падає з висоти h = 25 м. Визначити його середню швидкість \( \langle{v}\rangle \) на другій половині шляху.
Задача 1.12. По похилій дошці знизу вгору пустили кульку. На відстані S = 30 см від початкової точки кулька побувала двічі: через t1 = 1 c та t2 = 2 c . Визначити мінімально можливу довжину дошки L. Тертя відсутнє.
Задача 1.13. Тіло кинули зі швидкістю \( {v}_{0}\) = 15 м/с вертикально вгору з балкона, розташованого на висоті h = 25 м. Визначити: а) максимальну висоту підйому H тіла над землею; б) час \( \tau \), через який воно впаде на землю; в) швидкість \( {v}\) тіла на момент падіння.
Задача 1.14. Кабіна ліфта висотою h = 2,25 м починає підійматись із прискоренням a = 0,5 м/с2. На момент, коли її швидкість досягла значення \( {v}_{0}=2,5 \) м/с, зі стелі відірвалася пластилінова кулька. Визначити: а) час \( \tau \) падіння кульки на підлогу, б) величину (модуль) переміщення \( {l}\) та в) шлях S, який пройшла кулька відносно шахти ліфта.
| Задача 1.9 |
Літак рухається прямолінійно спочатку зі швидкістю \(v_{0}\) = 720 км/год, а потім протягом t = 10 с рівно-прискорено так, що за останню секунду (проміжок часу τ = 1 c) долає відстань S = 295 м.
Визначити
кінцеву швидкість літака \( {v}\).
Розв'язання
|
Дано: v0 = 720 км/год=
=200 м/с
t = 10 c
τ = 1 c
S = 295 м
|
|
\( {v}\) - ? |
Літак починає прискорюватися при заданій швидкості v0, тож шукана кінцева швидкість визначається рівнянням
|
\( {v}=v_{0}+at \). |
(1) |
Потрібне для отримання відповіді прискорення а можна знайти через заданий шлях S. Для цього в напрямку руху літака спрямуємо вісь OX із початком відліку в точці початку розгону, рис. 9. Тоді рівняння кінцевої координати літака має вигляд:
|
\( {x}=v_{0}t+\frac{at^{2}}{2}\). |
(2) |
Із цього ж рівняння, замінивши t на t1 = t – τ, отримаємо вираз координати на передостанню секунду:
\( {x}_{1}\) = \( v_{0}(t-\tau)+\frac{a(t-\tau)^{2}}{2}\).
Отже, літака за останню секунду S = x – x1 визначається, як
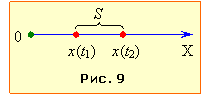
\( {S}=x-x_{1}\) = ${{v}_{0}}\tau +\frac{a\tau \left(2t-\tau \right)}{2}$,
Відтак після простих перетворень знайдемо прискорення
\( {a}=\frac{2(S-v_{0}\tau)}{{\tau}(2t-\tau)} \) = 10 м/с2
і за формулою (1) – кінцеву швидкість літака:
\( {v}\) = 300 м/с.
| Задача 1.10 |
Потяг, який рухається прямолінійно рівно-прискорено, на певній ділянці шляху збільшує швидкість на \( \Delta{v} \) = 60 км/год при середній швидкості \( \langle{v}\rangle \) = 40 км/год..
Визначити
швидкість поїзда \( {v}\) посередині згаданої ділянки.
|
Дано: \( \langle{v}\rangle \) = 40 км/год
\( \Delta{v}\) = 60 км/год
|
|
\( {v} \) - ? |
Розв'язання
В умові немає інформації про час руху потяга на згадуваній ділянці шляху. Тому пошук відповіді почнемо з формули (1.19), яка встановлює зв'язок між шляхом і швидкістю. Отже, увівши для початкової, кінцевої і шуканої швидкостей, а також прискорення і пройденого шляху відповідні позначення v1, v2, v, а, S, запишемо:
\({{v}^{2}}-v_{1}^{2}=aS\),
\({v_{2}^{2}-{v}^{2}}=aS\),
і, прирівнявши ліві частини, отримаємо:
| \({{v}^{2}}=\frac{v_{1}^{2}+v_{2}^{2}}{2}\) \(\Rightarrow \) v = \(\sqrt{{\left( v_{1}^{2}+v_{2}^{2} \right)}/{2}}\) | (1) |
Швидкості v1 і v2 можна виразити через задані величини \( \langle{v}\rangle \) і \( \Delta{v} \) за допомогою рівняння (1.16):
|
\(S={{v}_{1}}t+\frac{a{{t}^{2}}}{2}=\left( {{v}_{1}}+\frac{at}{2} \right)t\). |
Звідси, зробивши очевидні заміни S = \( \langle{v}\rangle\)t, a = (Δv/t) і v2 = v1 + Δv, дістанемо:
|
\({{v}_{1}}=\left\langle v \right\rangle -\frac{\Delta v}{2}\quad \ , \quad {{v}_{2}}=\left\langle v \right\rangle+\frac{\Delta v}{2}\) |
Відтак, підставивши отримані вирази у формулу (1), після спрощень отримуємо відповідь:
\( {v}=\sqrt{\langle{v}\rangle^{2}+\left(\frac{\Delta{v}}{2}\right)^{2}}\) = 50 км/год.
| Задача 1.11 |
Тіло вільно падає з висоти h = 25 м.
Визначити
його середню швидкість \( \langle{v}\rangle \) на другій половині шляху.
Дано:
| h = 25,0 м |
|
\( \langle{v}\rangle \)-? |
Розв'язання
Розв'яжемо задачу двома способами.
Спосіб 1. Середня швидкість тіла кульки дорівнює відношенню пройденого шляху (h/2) до часу його проходження Δt:
$\left\langle v \right\rangle =\frac{h}{2\Delta t}$,
Величина \( \Delta{t}=t_{2}-t_{1}\), де час проходження тілом верхньої половини шляху t1 і повний час руху t2 визначаються з рівняння (1.16):
\( \frac{h}{2}=\frac{gt_{1}^{2}}{2}\); \( \Rightarrow \) \( {t}_{1}=\sqrt{\frac{h}{g}}\);
\( {h}=\frac{gt_{2}^{2}}{2}\); \( \Rightarrow \) \( {t}_{2}=\sqrt{\frac{2h}{g}}\).
Отже,
\( \Delta{t}=t_{2}-t_{1}=\sqrt{\frac{h}{g}}\left(\sqrt{2}-1\right) \).
Відтак для шуканої і середньої швидкості виходить:
|
$\left\langle v \right\rangle =\frac{\sqrt{gh}}{2\left( \sqrt{2}-1 \right)}$ |
Помноживши цей вираз у чисельнику й знаменнику на $\left( \sqrt{2}+1 \right)$, відповідь можна подати також у наступному вигляді:
|
$\left\langle v \right\rangle =\frac{\sqrt{gh}}{2}\left( \sqrt{2}+1 \right)$. |
Обчислення дають
\(\left\langle v \right\rangle \) = 19 м/с
Спосіб 2. Відповідь можна отримати відразу за формулою (1.21) через швидкості тіла в кінці першої половини v1 та всього шляху v2, котрі за формулою (1.19а) дорівнюють
\({{v}_{1}}=\sqrt{gh}\) і \({{v}_{2}}=\sqrt{2gh}\)
Отже,
\(\left\langle v \right\rangle =\frac{\sqrt{gh}}{2}\left( \sqrt{2}+1 \right) \).
| Задача 1.12 |
Кулька, пущена вгору по похилій дошці, на відстані S = 30 см від початкового положення побувала двічі: через t1 = 1 c та t2 = 2 c .
Визначити
мінімально можливу довжину дошки L. Тертя відсутнє.
|
Дано: S = 30 см
t1 = 1 c
t2 = 2 c
|
|
L - ? |
Розв'язання
Кулька рухається вздовж дошки з наданою їй початковою швидкістю v0 і прискоренням a, що створюється "скочувальною" складовою сили тяжіння. Спочатку вона опиняється на відстані S в момент t1, підіймаючись угору, а потім у момент t2 знов опиняється в тому самому положенні, скочуючись. Отже, найменша необхідна довжина дошки дорівнює максимальній відстані L, на яку може віддалитися кулька від початкового положення.
Для визначення величини L спрямуємо вісь OX уздовж дошки, розмістивши початок координат в початковому положенні кульки (х0 = 0). У такому разі проєкція прискорення ах = – а, і, згідно з рівнянням (1.18),
| \(x=\frac{v_{0}^{2}-{{v}^{2}}}{2a}\). |
При максимальному віддаленні х = L швидкість кульки v = 0, отже,
| \( {L}=\frac{v_{0}^{2}}{2a}\). | (1) |
Величини v0 і a можна знайти з рівняння координати кульки (1.16). Поклавши x = S , отримаємо:
|
\( {S}=v_{0}t-\frac{at^{2}}{2}\) \(\Rightarrow \) \(a{{t}^{2}}-2{{v}_{0}}t+2S=0\), |
Коренями цього рівняння є задані моменти часу t1 і t2, тож за теоремою Вієта
${{t}_{1}}+{{t}_{2}}=\frac{2{{v}_{0}}}{a}$ i ${{t}_{1}}{{t}_{2}}=\frac{S}{2a}$,
і
\( {a}=\frac{2S}{t_{1}t_{2}}\), \( {v}_{0}=\frac{a(t_{1}+t_{2})}{2}=\frac{S(t_{1}+t_{2})}{t_{1}t_{2}}\).
Підставивши отримані величини у вираз (1), дістанемо відповідь:
\( {L}=\frac{S(t_{1}+t_{2})^{2}}{4t_{1}t_{2}}\) ≈ 34 см.
| Задача 1.13 |
Тіло кинули зі швидкістю \( {v}_{0}\) = 15 м/с вертикально вгору з балкона, розташованого на висоті h = 25 м.
Визначити:
а) максимальну висоту підйому H тіла над землею;
б) час \( \tau \), через який воно впаде на землю;
в) швидкість \( {v}\) тіла на момент падіння.
|
Дано: h = 25 м
v0 = 15 м/с
|
|
H - ?
τ - ?
v - ?
|
Розв'язання
Напрямимо вгору вісь OY з початком відліку на землі (рис. 13). У такому разі початкова координата тіла y0 = h, проєкції швидкості та прискорення \(v_{0y}=v_{0}\) і \(g_{y}=-g\), і, згідно з (1.16), 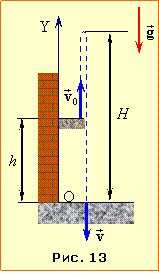 поточні координата та проєкція швидкості задовольняють рівняння:
поточні координата та проєкція швидкості задовольняють рівняння:
| \(y=h+v_{0}t-\frac{gt^{2}}{2}\), | (1) |
| vy = v0 – gt. | (2) |
а) У найвищій точці підйому швидкість тіла дорівнює нулю, тож час підйому:
| \(t=\frac{v_{0}}{g}\). |
Максимальна висота підйому дорівнює координаті тіла в цей момент:
\(H=h+v_{0}t-\frac{gt^{2}}{2}=h+\frac{v_{0}^{2}}{2g}\approx\) 36,5 м.
б) На момент падіння на землю t =\(\tau\) координата тіла y = 0:
\(y(\tau)=h+v_{0}\tau-\frac{g\tau^{2}}{2}=\) 0.
Розв'язавши це квадратне рівняння, знайдемо:
\(\tau=\frac{v_{0}+\sqrt{v_{0}^{2}+2gh}}{g}=\) 4,26 c.
(від'ємний корінь не має фізичного змісту).
в) Підставивши знайдене значення \(\tau\) в рівняння (2), дістанемо
vy = v0 – gτ= –26,75 м/с.
Знак "–" означає, що вектор швидкості в момент падіння тіла на землю напрямлений проти осі OY, тобто вертикально вниз.
| Задача 1.14 |
Кабіна ліфта висотою h = 2,25 м починає підійматися з прискоренням a = 0,5 м/с2. У момент, коли її швидкість досягла значення v0 = 2,5 м/с, зі стелі відірвалася пластилінова кулька.
Визначити:
а) час \( \tau \) руху кульки до підлоги;
б) переміщення \( {l}\) та
в) шлях S, який пройшла кулька відносно шахти.
|
Дано: h = 2,25 м
a = 0,5 м/с2
v0 = 2,5 м/с
|
|
τ - ? l - ? S - ? |
Розв'язання
Рух кульки, залежно від ситуації, зручно розглядати або відносно кабіни ліфта (система відліку O′Y′, рис. 1.14а), або відносно шахти (система відліку OY, рис. 1.14б).
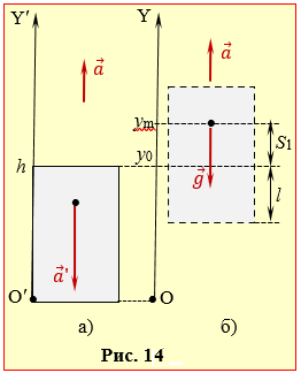 а) Для визначення часу падіння кульки є доцільно розглянути її рух відносно кабіни ліфта (рухомої системи відліку О′Y′ рис. 14а).
а) Для визначення часу падіння кульки є доцільно розглянути її рух відносно кабіни ліфта (рухомої системи відліку О′Y′ рис. 14а).
Відносно землі ліфт рухається з прискоренням \( \vec{a}\) а кулька – з прискоренням \( \vec{g}\). Тож відносно ліфта її прискорення \( \vec{a}^{\prime}=\vec{g}-\vec{a}\) має модуль
a′ = (a + g).
При цьому початкова швидкість кульки відносно ліфта ${{{v}'}_{0}}=0$ і початкова координата ${{{y}'}_{0}}=h$. Отже за рівнянням (1.16) її координата в довільний момент часу
\( {y}^{\prime}=h-\frac{(g+a)t^{2}}{2}\).
Тож на момент падіння t = \( \tau \), коли \( {y}^{\prime}\) = 0, маємо:
\( h-\frac{(g+a)t^{2}}{2}={0}\) \( \Rightarrow \) \( \tau=\sqrt{\frac{2h}{g+a}}\) = 0,65 c.
б) Величина переміщення l кульки в нерухомій системі відліку OY , що є пов'язана із шахтою ліфта (тобто землею), дорівнює відстані (модулю різниці координат) між точками падіння на підлогу та відриву кульки від стелі ліфта:
$l=\left| y(\tau )-h \right|$.
Прискорення кульки відносно шахти дорівнює g, отже,
\( {y}(\tau)=h+v_{0}\tau-\frac{g{\tau}^{2}}{2}\).
Відповідно, переміщення
| \( {l}=\left|v_{0}\tau-\frac{g\tau^{2}}{2}\right|={0,5}\) м. | (1) |
в) На рис. 1.14б умовно показано положення кабіни ліфта відносно шахти (в системі відліку OY) на момент падіння кульки на підлогу та її початкове (y0 = h) і найвище (ym) положення. З рисунка видно, що шлях S кульки складається з двох частин – шляху підйому до найвищої точки траєкторії S1 і шляху S2 падіння на підлогу ліфта, причому \( {S}_{2}=S_{1}+{l}\). Отже,
| \( {S}=S_{1}+S_{2}=2S_{1}+{l}\) |
Позаяк у найвищій точці підйому швидкість кульки v = 0, то згідно з формулою (1.19),
\( {S}_{1}=\frac{v_{0}^{2}}{2g}\) = 0,3 м,
і згідно з результатом (1) шуканий шлях кульки від точки відриву до підлоги ліфта складає
S = 1,1 м.