ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Розділ І. КІНЕМАТИКА
1.5. Рівномірний рух по колу
Одним із поширених простих рухів є рівномірний рух по колу, що визначається радіусом кола R та швидкістю v, яка в цьому випадку називається лінійною швидкістю.
Рівномірне обертання є циклічним рухом, тому його характеризують також періодом T і частотою n.
Періодом T (с) називається час, за який тіло здійснює один повний оберт по колу.
Частота n (об/с) – це кількість обертів, яку тіло здійснює за одиницю часу:
| \( {n}=\frac{1}{T} \). | (1.22) |
Зв’язок між швидкістю і періодом (частотою) обертання:
|
\(v=\frac{2\pi R}{T}=2\pi Rn\) |
(1.23) |
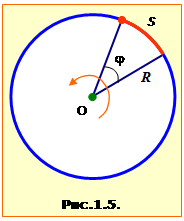
Крім указаних величин при описі колового руху точки та обертання твердого тіла використовують також кутові величини: кут повороту та кутову швидкість.
| \( \varphi=\frac{S}{R} \). | (1.24) |
| \( \omega=\frac{\Delta\varphi}{\Delta{t}} \). | (1.25) |
Лінійна та кутова швидкості пов'язані співвідношенням
| \( {v}=\omega{R} \), | (1.26) |
а кутова швидкість і період (частота) обертання – співвідношенням
| \( \omega=\frac{2\pi}{T}=2\pi{n} \). | (1.27) |
При рівномірному обертовому русі модуль лінійної швидкості не змінюється, але змінюється її напрям. Тому такий рух характеризується доцентровим прискоренням, модуль якого визначається виразами:
| aдц = \( \frac{v^{2}}{R}=4\pi^{2}n^{2}R=\frac{4\pi^{2}R}{T^{2}}=\omega^{2}R=\omega{v} \). | (1.28) |
Вектор доцентрового прискорення ${{\vec{a}}_{\text{дц}}}$ є напрямлений до центра кола, по якому рухається точка.