ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Розділ І. КІНЕМАТИКА
1.2. Відносність руху
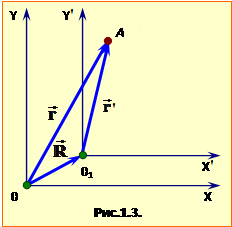
Положення тіла в просторі є визначеним не саме по собі, а тільки по відношенню до вибраної ''системи відліку'' – якогось іншого тіла й жорстко зв'язаної з ним системи координат. Те саме стосується й руху, тож він за самою природою є відносним. Через це положення точки та її рух у двох різних системах відліку – нерухомій (ХОY) та рухомій (Х′О′Y′) – визначаються різними, хоч і взаємопов'язаними, значеннями радіус-вектора, швидкості та прискорення. Радіус-вектори \( \vec{r}\) і \(\vec{r}^{\prime}\) точки в нерухомій та в рухомій системі відліку (рис.1.3) є зв'язані співвідношенням:
| \( \vec{r}={\vec{r}}'+\vec{R}\), | (1.9) |
де \( \vec{R} \) – радіус-вектор, що задає положення початку відліку рухомої системи відносно нерухомої (рис.1.3). Аналогічно для переміщень
| $\Delta \vec{r}=\Delta \vec{{r}'}+\Delta \vec{R}$ | (1.9а) |
Звідси відповідно до формули (1.4) випливає класичний закон додавання швидкостей:
| \( \vec{v}={\vec{v}}'+\vec{V}\) | (1.10) |
 |
тобто,
вектор швидкості тіла в нерухомій системі відліку \( \vec{v}\) дорівнює сумі вектора його швидкості в рухомій системі відліку ${\vec{v}}'$ та вектора швидкості \( \vec{V} \) рухомої системи відліку відносно нерухомої.
Швидкість \(\vec{v}^{\prime}\) тіла відносно рухомої системи через його швидкість \( \vec{v}\) у нерухомій системі визначається зворотнім співвідношенням:
| \( {\vec{v}^{\prime}}=\vec{v}-\vec{V}\). | (1.10а) |
Співвідношення (1.11) і (1.11а) є універсальними і виконуються в будь-яких системах відліку та при будь-яких рухах тіла. Але зв'язок між прискореннями є більш складним і залежить від систем відліку. І тільки в системах відліку, що рухаються одна відносно одної поступально, прискорення тіла \( \vec{a}\) і \({\vec{a}}'\) пов'язані таким самим співвідношенням, що й швидкості:
|
\(\vec{a}={\vec{a}}'+{{\vec{a}}_{0}}\) |
(1.11) |
i
|
\({\vec{a}}'=\vec{a}-{{\vec{a}}_{0}}\) |
(1.11а) |
де \( \vec{a}_{0}\) – прискорення рухомої системи відліку відносно нерухомої.