ФІЗИКА. Вчимося розв'язувати задачі. "СУЧАСНА ФІЗИКА". Компенсаційний курс
| Сайт: | physics.zfftt.kpi.ua |
| Курс: | physics.zfftt.kpi.ua |
| Книга: | ФІЗИКА. Вчимося розв'язувати задачі. "СУЧАСНА ФІЗИКА". Компенсаційний курс |
| Напечатано:: | |
| Дата: | Суббота, 27 июля 2024, 06:01 |
Оглавление
Частина 6. Вступ
|
Механіка Ньютона і електродинаміка Максвелла складають фундамент класичної фізики. Положення цих наук використовуються також в інших розділах фізики. Так наприклад, у класичній молекулярно-кінетичній теорії використовують уявлення ньютонівської механіки, а в оптиці - положення класичної теорії електромагнітного поля. Однак ці науки, як і інші фізичні теорії, мають обмежену область застосування. Виявилося, що закони класичної механіки не придатні до рухів зі швидкостями близькими до швидкості світла (\(c = 3\cdot{10}^{8}\) м/с) і рухів мікроскопічних частинок, якими є елементарні частинки і атоми. Тіла, що складаються з дуже великої кількості атомів, називаються макроскопічними, хоча вони можуть мати дуже малі за звичайними мірками розміри (наприклад, \(10^{-6}\) м або навіть менше). Аналогічно, закони класичної електродинаміки не дають правильного пояснення механізмів виникнення електромагнітного випромінювання і його взаємодії з частинками речовини. Аналіз причин обмеженості класичних теорій призвів до створення спеціальної теорії відносності (механіки надшвидких рухів, або як її ще називають - релятивістської механіки) і квантової механіки (теорії руху мікроскопічних частинок). Ці теорії, а також інші розділи фізики, що виникли на її основі, складають сучасну фізику. Звичайно, цей термін не слід розуміти буквально: "сучасна" фізика існує вже 100 років. Але в той ж час деякі її розділи (наприклад, теорія елементарних частинок і космологія) ще не завершені і знаходяться в стадії інтенсивного розвитку. Даний посібник містить основні положення з розділів: 18. Елементи спеціальної теорії відносності |
Розділ 18. Елементи спеціальної теорії відносності
|
Спеціальна теорія відносності (СТВ), створена Ейнштейном, вивчає рух тіл із субсвітловими (v ~ c) швидкостями в інерціальних системах відліку. Незастосовність до таких рухів співвідношень механіки Ньютона, як виявилося, пов'язана з принциповою помилковістю уявлень класичної фізики про деякі властивості простору і часу. Тому в широкому розумінні спеціальна теорія відносності є сучасною фізичною теорією простору і часу. У СТВ піддані ревізії і радикально змінені здавалося б непорушні уявлення про розмір тіл, проміжки часу, швидкості, імпульс і масу, енергію та ін. Теоретичні відомості |
18.1. Постулати СТВ
|
В основі спеціальної теорії відносності лежать два постулати (постулати – вихідні твердження, що приймаються в даній теорії без формально-логічного доказу. У фізиці постулати встановлюються на основі експериментальних фактів. Наприклад, постулатами класичної механіки є закони Ньютона). 1. Принцип відносності Ейнштейна:
Це означає, що
2. Постулат сталості швидкості світла:
У класичній фізиці принцип відносності був відомий тільки для механічних явищ (механічний принцип відносності називають ще принципом відносності Галілея). Після створення електродинаміки з'ясувалося, що він справедливий і для електромагнітних явищ. Виходячи з цього Ейнштейн постулював, що принцип відносності поширюється на фізичні явища будь-якої природи, тобто надав йому рангу абсолютного закону природи. Можна сказати, що принцип відносності затверджує повну рівноправність усіх інерціальних систем відліку. Другий постулат, на перший погляд, суперечить здоровому глузду. Дійсно, нехай у системі відліку, зв'язаній з Землею, закріплена лампочка, що світиться. Світло від неї поширюється у вакуумі в усі сторони зі швидкістю для спостерігача на Землі. Другий постулат стверджує, що відносно космічної ракети, яка пролітає повз спостерігача на Землі з великою швидкістю, світло цієї ж лампочки теж поширюється зі швидкістю . Це може здатися дивним, але численні експериментальні факти підтверджують цей висновок. Те, що світло від одного джерела поширюється у всіх системах відліку з однаковою швидкістю, свідчить про існування в природі граничної швидкості. Це означає, що
|
18.2. Відносність довжин і проміжків часу
|
Наслідки з постулатів СТВ різко суперечать багатьом принциповим положенням класичної механіки. Це насамперед стосується простору і часу. Класична фізика виходить з уявлень про абсолютність простору і часу. Але постулати СТВ свідчать про відносність простору і часу. |
|
З механіки відомо, що положення тіла в просторі відносне – його можна визначити тільки відносно обраної системи відліку. Але сам простір у класичній фізиці розглядався як абсолютний, тобто як єдиний для усього Всесвіту й однаковий за властивостями у всіх системах відліку. З цієї концепції випливає очевидний висновок: хоча координати будь-якої точки в двох системах відліку XOY і X′O′Y′ (рис.18.1) різні (\(X\ne{X}^{\prime}\), \(Y\ne{Y}^{\prime}\)) відстань l між двома точками А і В однакова. Інакше кажучи, взаємне положення точок і розміри тіл у класичній фізиці вважається абсолютними.
Точно так само і час вважався абсолютним. У різних часових поясах Землі поточні моменти часу виражаються різними числами, але одночасність двох подій, або проміжок часу, що розділяє дві події, вважаються абсолютними, тобто не залежними від вибору системи відліку. |
18.3. Відносність довжин і проміжків часу
|
Наслідки з постулатів СТВ різко суперечать багатьом принциповим положенням класичної механіки. Це насамперед стосується простору і часу. Класична фізика виходить з уявлень про абсолютність простору і часу. Але постулати СТВ свідчать про відносність простору і відносність часу. |
|
З механіки відомо, що положення тіла в просторі відносне – його можна визначити тільки відносно обраної системи відліку. Але сам простір у класичній фізиці розглядався як абсолютний, тобто як єдиний для усього Всесвіту й однаковий за властивостями у всіх системах відліку. З цієї концепції випливає очевидний висновок: хоча координати будь-якої точки в двох системах відліку XOY і X’O’Y’ (рис.18.1) різні (\(X\ne{X}^{\prime}\), \(Y\ne{Y}^{\prime}\)) відстань l між двома точками А і В однакова. Інакше кажучи, взаємне положення точок і розміри тіл у класичній фізиці вважається абсолютними.
Точно так само і час вважався абсолютним. У різних часових поясах Землі поточні моменти часу виражаються різними числами, але одночасність двох подій, або проміжок часу, що розділяє дві події, вважаються абсолютними, тобто не залежними від вибору системи відліку. |
18.4. Релятивістський закон додавання швидкостей
|
Сталість швидкості світла у вакуумі в різних системах відліку свідчить про те, що і формула додавання швидкостей класичної механіки (1.9) теж принципово невірна. У СТВ діє релятивістський закон додавання швидкостей. |
|
Системи відліку XOY та X′O′Y′ мають співпадаючі осі OX, O′X′ і однаково напрямлені осі OY, O′Y′ (та OZ, O′Z′), причому система відліку X′O′Y′ рухається в додатному напрямку осі OX зі швидкістю V = const. Якщо деяка матеріальна точка A (тіло) теж рухається паралельно осям X, X′, то зв′язок між швидкостями точок в цих системах відліку визначається релятивістським законом додавання швидкостей:
де vx – проекція швидкості точки в системі XOY, \(v_{x}^{\prime}\) – проекція швидкості в системі X′O′Y′. Для проекції \(v_{y}\), \(v_{y}^{\prime}\) і \(v_{z}\), \(v_{z}^{\prime}\) формули мають інший вигляд і в елементарній фізиці не розглядаються. Насамперед звернемо увагу на те, що при малих швидкостях (\(v_{x}\ll{c}\), \(V\ll{c}\)) величина \(v_{x}V/c^{2}\ll{1}\) та \(v_{x}^{\prime}V/c^{2}\ll{1}\), тобто формули СТВ (18.3) і (18.3а) автоматично трансформуються у відповідні класичні формули (1.9) і (1.10): \(v_{x}=v_{x}^{\prime}+V\) і \(v_{x}^{\prime}=v_{x}-V\). Іншою особливістю формул (18.3), (18.3а) є те, що при будь-яких значеннях \(v_{x}^{\prime}\) і V виходить \(v_{x}\le{c}\) (див. задачу 18.1). Зокрема, якщо \(v_{x}^{\prime}={c}\), то й \(v_{x}={c}\), тобто релятивістський закон додавання швидкостей узгоджується з постулатом сталості швидкості світла у вакуумі й існуванням граничної швидкості c. |
18.5. Релятивістський імпульс і маса
|
Одна з найважливіших динамічних характеристик руху – імпульс – теж має більш складні властивості, ніж вважалося в класичній механіці. |
|
Імпульс частинки, що швидко рухається (релятивістської частинки), і має швидкість v, визначається формулою релятивістського імпульсу:
Величина m, яка визначена формулою (18.5), називається релятивістською масою частинки, а m0 – масою спокою. Формулу (18.5) часто інтерпретують як свідчення залежності маси (інертності) від швидкості. При розгоні і наближенні швидкості тіла до значення c (\(v\to{c}\)) його інертність необмежено зростає (\(m\to\infty\)). Цим пояснюється неможливість руху тіла зі швидкістю, яка не тільки більша, але навіть точно рівна граничній швидкості c. Виключення складають так звані безмасові частинки, у яких m0 = 0, і швидкість точно дорівнює . Такими частинками є фотони. При малих швидкостях руху (\(v/c\to{0}\)) формули (18.5), (18.4а) і (18.4) дають: \(m=m_{0}\), (const) \(\vec{p}=m_{0}\vec{v}\), тобто при малих швидкостях руху справедливі твердження класичної механіки про те, що маса тіла є величина постійна й імпульс прямо пропорційний швидкості. |
18.6. Закон взаємозв'язку маси і енергії
|
У теорії відносності встановлюється також закон взаємозв'язку між масою та енергією, з якого, зокрема, випливає формула кінетичної енергії релятивістської частинки. |
|
У природі діє універсальний закон взаємозв'язку між масою та енергією, відповідно до якого будь-яке тіло має енергію
де m – релятивістська маса тіла, m0 – маса спокою, c – гранична швидкість. Величина E називається повною релятивістською енергією. Вона включає кінетичну енергію тіла і всі види внутрішньої енергії, але не включає "зовнішню" потенціальну енергію, тобто потенціальну енергію тіла у зовнішньому полі (наприклад, гравітаційному або електричному) і енергію взаємодії даного тіла з іншими тілами. Цей закон універсальний: він виконується для будь-яких матеріальних об'єктів, включаючи елементарні частинки, і за будь-яких умов. Зокрема, нерухома частинка має відповідну енергію спокою E0:
Це означає, що будь-яка частинка має певний запас енергії тільки завдяки самому факту свого існування, тобто
Відповідно до співвідношення (18.6), будь-якій зміні енергії \(\Delta{E}\) відповідає еквівалентна зміна маси \(\Delta{m}\), і навпаки:
Це стосується як енергії, так і маси спокою (формула (18.6б)), тобто енергія (і маса) спокою повинні при відповідних умовах перетворюватися в інші форми. Так і є в дійсності. Наприклад, при утворенні атомного ядра виділяється дуже велика енергія, і маса спокою ядра будь-якого елемента менша за суму мас спокою часток (нуклонів), з яких воно складається. |
|
Закон взаємозв'язку маси і енергії дозволяє одержати вираз для кінетичної енергії релятивістської частинки. Кінетична енергія T – це енергія руху. Тому вона дорівнює різниці повної енергії (формула (18.6)) і енергії спокою (18.6a) частинки:
або, відповідно до формули (18.5),
Ця формула теж суттєво відрізняється від класичної, але при \(v/c\ll{1}\) перетворюється на неї: \(T=\frac{m_{0}v^{2}}{2}\). (У цьому можна переконатися, використавши у виразі (18.9) відому з математики формулу наближених обчислень \((1+x)^{n}=1+nx\), якщо \(x\ll{1}\). У нас \(x=-v^{2}/c^{2}\), \(n=-1/2\)). |
Приклади розв'язування задач
Задача 18.1. Визначити власну довжину стержня l0, якщо в лабораторній системі відліку його швидкість v = c/2, довжина l = 1,00 м і кут між ним і напрямком руху \(\theta=45^{\circ}\).
Задача 18.2. Власний час життя нестабільної елементарної частинки \(\Delta{t}_{0}=10\) нс. У лабораторній системі відліку, відносно якої частинка рухається, час її життя \(\Delta{t}=20\) нс. Визначити відстань l, яку пролітає частинка в лабораторній системі відліку до розпаду.
Задача 18.3. Стержень пролітає з постійною швидкістю повз мітку, зроблену в нерухомій K- системі відліку. Час прольоту за годинником K-системи \(\Delta{t}=20\) нс. У системі відліку K’, зв'язаній зі стержнем, мітка рухається повз нього протягом \(\Delta{t}^{\prime}=25\) нс. Визначити власну довжину стержня l0.
Задача 18.4. Дві частинки рухаються назустріч одна одній зі швидкостями v1 = 0,50c і v2 = 0,75c (c – швидкість світла). Визначити: А) відносну швидкість частинок vвідн; Б) швидкість u, з якою зменшується відстань між частинками в лабораторній системі відліку.
Задача 18.5. Швидкість частинки відрізняється від швидкості світла на k = 0,01 %. Визначити відношення релятивістської маси частинки до її маси спокою m/m0.
Задача 18.6. Протон має імпульс p = 10,0 ГеВ/с, де – швидкість світла. Визначити відносну відміну k (у %) швидкості протона від швидкості світла c.
Задача 18.7. Визначити імпульс протона p, кінетична енергія котрого T = 500 МеВ.
Задача 18.8. Визначити роботу A, яку необхідно виконати, щоб змінити швидкість протона від v1 = 0,6c до v2 = 0,8c.
Задача 18.9. Енергія сонячного випромінювання, яке нормально падає щосекунди на одиничну площадку на поверхні Землі, дорівнює I = 1,4 кДж/(м2·с) (ця величина називається сонячною сталою і не враховує поглинання та розсіювання сонячного випромінювання атмосферою Землі). Прийнявши середній радіус земної орбіти R = 149,5·106 км і масу Сонця M = 2·1030 кг, визначити: А) масу \(\mu\), що втрачає Сонце за одиницю часу; Б) час t, за який маса Сонця зменшилася б на k = 1 % при незмінній інтенсивності випромінювання.
Задача 18.1
Визначити
власну довжину стержня l0, якщо в лабораторній системі відліку його швидкість v = c/2, довжина l = 1,00 м і кут між ним і напрямком руху \(\theta=45^{\circ}\).
|
Дано: v = c/2
l = 1,00 м
\(\theta=45^{\circ}\)
|
|
l0 - ?
|
Розв’язання
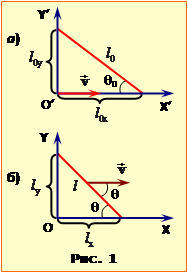 Нехай стержень у власній системі відліку X’O’Y’ (тобто такій, де він перебуває у спокої), розташований так, як показано на рис.1а. Його довжина в цій системі визначається довжинами відрізків l0x і l0y:
Нехай стержень у власній системі відліку X’O’Y’ (тобто такій, де він перебуває у спокої), розташований так, як показано на рис.1а. Його довжина в цій системі визначається довжинами відрізків l0x і l0y:
|
\(l_{0}=\sqrt{l_{0x}^{2}+l{oy}^{2}}\). |
(1) |
Для спостерігача лабораторної системи відліку XOY довжини відрізків, що відсікаються кінцями стержня на осях OX та OY, згідно з формулою (18.1), рівні:
\(l_{x}=l_{0x}\sqrt{1-\beta^{2}}\), \(l_{y}=l_{0y}\),
де \(\beta=v/c\). З рис.1б зрозуміло, що
\(l_{x}=l\cos\theta\), \(l_{y}=l\sin\theta\).
Тому
\(l_{0x}=\frac{l\cos\theta}{\sqrt{1-\beta^{2}}}\), \(l_{0y}=l\sin\theta\).
Підставивши ці вирази у формулу (1), одержимо:
\(l_{0}=l\sqrt{\frac{1-\beta^{2}\sin^{2}\theta}{1-\beta^{2}}}=1,00\cdot\sqrt{\frac{1-0,25\cdot{0,5}}{1-0,25}}=1,08\) м.
Задача 18.2
Власний час життя нестабільної елементарної частинки \(\Delta{t}_{0}=10\) нс. У лабораторній системі відліку, відносно якої частинка рухається, час її життя \(\Delta{t}=20\) нс.
Визначити
відстань l, яку пролітає частинка в лабораторній системі відліку до розпаду.
|
Дано: Δt0 = 10 нс
Δt = 20 нс
|
|
l - ?
|
Розв’язання
Проміжок часу між двома подіями в різних системах відліку зв'язаний співвідношенням (18.2):
\(\Delta{t}=\frac{\Delta{t}_{0}}{\sqrt{1-\beta^{2}}}\),
де \(\beta=v/c\). З цього співвідношення визначаємо швидкість руху частинки в заданій системі відліку
\(v=c\sqrt{1-(\Delta{t}_{0}/\Delta{t})^{2}}\).
Пройдений частинкою шлях
\(l=v\cdot\Delta{t}=c\cdot\Delta{t}\sqrt{1-(\Delta{t}_{0}/\Delta{t})^{2}}=3\cdot{10}^{8}\cdot{20}\cdot{10}^{-9}\cdot\sqrt{1-(10/20)^{2}}\approx{5,2}\) м.
Примітка
Під коренем стоїть відношення проміжків часу, тому при обчисленнях можна користуватися будь-якими, але однаковими, одиницями часу.
Задача 18.3
Стержень пролітає з постійною швидкістю повз мітку, зроблену в нерухомій K- системі відліку. Час прольоту за годинником K-системи \(\Delta{t}=20\) нс. У системі відліку K’, зв'язаній зі стержнем, мітка рухається повз нього протягом \(\Delta{t}^{\prime}=25\) нс.
Визначити
власну довжину стержня l0.
|
Дано: Δt = 20 нс
Δt′ = 25 нс
|
|
l0 - ?
|
Розв’язання
Для спостерігача K- системи відліку час прольоту стержня
|
\(\Delta{t}={l}/{v}\), |
(1) |
де v – швидкість стержня, l – його довжина в K – системі, яка зв'язана з власною довжиною l0 співвідношенням (18.1):
|
\(l=l_{0}\sqrt{1-\beta^{2}}\), |
(2) |
де \(\beta=v/c\).
У K′- системі стержень нерухомий і має довжину l0, тому час прольоту мітки повз нього
|
\(\Delta{t}^{\prime}=\frac{l_{0}}{v}\). |
(3) |
Підставивши у формулу (1) вираз (2) і врахувавши (3), знаходимо
\(\Delta{t}=\Delta{t}^{\prime}\sqrt{1-\beta^{2}}\) \(\Rightarrow\) \(v=c\sqrt{1-(\Delta{t}/\Delta{t}^{\prime})^{2}}\).
Підставивши це значення у формулу (3), одержимо
\(l_{0}=c\cdot\Delta{t}^{\prime}\cdot\sqrt{1-(\Delta{t}/\Delta{t}^{\prime})^{2}}=3\cdot{10}^{8}\cdot{2,5}\cdot{10}^{-8}\sqrt{1-(20/25)^{2}}=4,5\) м.
Задача 18.4
Дві частинки рухаються назустріч одна одній зі швидкостями v1 = 0,50c і v2 = 0,75c (c – швидкість світла).
Визначити:
А) відносну швидкість частинок vвідн;
Б) швидкість u, з якою зменшується відстань між частинками в лабораторній системі відліку.
|
Дано: v1 = 0,50c
v2 = 0,75c
|
|
vвідн - ?
u - ?
|
Розв’язання
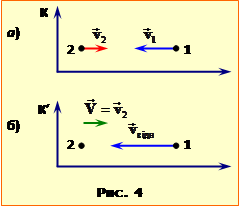 A) Для визначення відносної швидкості частинок перейдемо в систему відліку K′, яка має швидкість \(\vec{V}=\vec{v}_{2}\) відносно системи відліку K (рис.4). Тоді швидкість частинки 2 в K′ – системі \(\vec{v}_{2}^{\prime}=0\). Швидкість частинки 1 \(\vec{v}_{1}^{\prime}\) – то є швидкість її руху відносно частинки 2, тобто – шукана відносна швидкість: \(\vec{v}_{відн}=\vec{v}_{1}^{\prime}\). Отже, згідно з формулою (18.3), відносна швидкість частинок
A) Для визначення відносної швидкості частинок перейдемо в систему відліку K′, яка має швидкість \(\vec{V}=\vec{v}_{2}\) відносно системи відліку K (рис.4). Тоді швидкість частинки 2 в K′ – системі \(\vec{v}_{2}^{\prime}=0\). Швидкість частинки 1 \(\vec{v}_{1}^{\prime}\) – то є швидкість її руху відносно частинки 2, тобто – шукана відносна швидкість: \(\vec{v}_{відн}=\vec{v}_{1}^{\prime}\). Отже, згідно з формулою (18.3), відносна швидкість частинок
\(v_{відн}=\frac{v_{1}-v_{2}}{1+v_{1}\cdot{v}_{2}/c^{2}}=-\frac{0,5c+0,75c}{1+0,5c\cdot{0,75}c/c^{2}}=-\frac{1,25c}{1,376}=-0,91c=-2,73\cdot{10}^{8}\) м/с.
Знак "–" вказує напрям руху частинки 1 (протилежно напрямку осі OX).
Зауважимо, що навіть якби швидкості частинок були рівні c (частинки – фотони), їхня відносна швидкість була б
\(v_{відн}=\frac{c+c}{1+c\cdot{c}/c^{2}}=c\).
Це ілюструє граничність швидкості c.
Б) У лабораторній системі відліку частинки проходять за час t відстані l1 = v1t і l2 = v2t наближаючись одна до одної на відстань l = v1t + v2t = (v1 + v2)t Отже швидкість u з якою зменшується відстань між частинками в лабораторній системі відліку,
\(u=\frac{l}{t}=v_{1}+v_{2}=0,5c+0,75c=1,25c\).
Те, що отримана величина u > c ніяк не суперечить існуванню в природі граничної швидкості c. Знайдена величина є швидкістю зміни відстані між частинками для стороннього спостерігача. Але вона не є швидкістю руху жодної з частинок.
Задача 18.5
Швидкість частинки відрізняється від швидкості світла на k = 0,01 %.
Визначити
відношення релятивістської маси частинки до її маси спокою m/m0.
|
Дано: k = 0,01 %
|
|
m/m0 - ?
|
Розв’язання
Згідно з формулою (18.5)
|
\(\frac{m}{m_{0}}=\frac{1}{\sqrt{1-\beta^{2}}}\), |
(1) |
де \(\beta=v/c\), v – швидкість частинки, c – швидкість світла.
За умовою задачі
\(k=\frac{c-v}{c}\) \(\Rightarrow\) \(v=(1-l)\cdot{c}\) \(\Rightarrow\) \(\beta=1-k\)
Підставивши це значення у вираз (1), знаходимо
\(\frac{m}{m_{0}}\frac{1}{\sqrt{2k+k^{2}}}\approx\frac{1}{\sqrt{2k}}=70,7\)..
де ми знехтували k2 у порівнянні з 2k у зв'язку з малістю цієї величини.
Задача 18.6
Протон має імпульс p = 10,0 ГеВ/с, де – швидкість світла.
Визначити
відносну відміну k (у %) швидкості протона від швидкості світла c.
|
Дано: p = 10,0 ГеВ/с
|
|
k (%) - ?
|
Розв’язання
Відносна відміна швидкості частинки від швидкості світла визначається виразом
|
\(k=\frac{c-v}{c}=1-\frac{v}{c}=1-\beta\), |
(1) |
де \(\beta=v/c\).
Таким чином, розв'язання задачі зводиться до визначення \(\beta\). Для цього скористаємося виразом релятивістського імпульсу (18.4):
\(p=\frac{m_{0}v}{\sqrt{1-\beta^{2}}}\),
де m0 – маса спокою частинки.
Домножимо обидві частини на \(c^{2}\) і піднесемо цей вираз до квадрата:
\((pc^{2})^{2}=\frac{(m_{0}c^{2})^{2}v^{2}}{1-\beta^{2}}\) \(\Rightarrow\) \(\frac{p^{2}c^{2}}{E_{0}^{2}}=\frac{\beta^{2}}{1-\beta^{2}}\),
де \(E_{0}=m_{0}c^{2}=938,3\) МеВ – енергія спокою протона.
З цієї рівності після перетворень знаходимо \(\beta\)
\(\beta=\frac{1}{\sqrt{(E_{0}/pc)^{2}+1}}\),
і з виразу (1) дістаємо відповідь:
\(k=1-\frac{1}{\sqrt{(E)_{0}/pc)^{2}+1}}=1-\frac{1}{\sqrt{(938,3/10\cdot{10}^{3})^{2}+1}}=0,00473\approx0,44\) %.
Примітка. Для елементарних частинок основні одиниці виміру енергії (Дж) і імпульсу (кг·м/с) дуже незручні – занадто великі. Тому використовують позасистемні одиниці енергії: електрон-вольт (1 еВ = \(1,6\cdot{10}^{-19}\) Дж), мегаелектрон-вольт (читається «мев», 1 МеВ = \(10^{6}\) еВ) і гігаелектрон-вольт («гев», 1 ГеВ = \(10^{9}\) еВ). Для імпульсу швидких (релятивістських) частинок теж застосовують специфічну одиницю 1 ГеВ/с, де с – швидкість світла у вакуумі (а не позначення секунди). Це дуже зручно, тому що числові значення імпульсу в таких одиницях дорівнюють величині pc, яка часто зустрічається в задачах релятивістської механіки.
Задача 18.7
Визначити
імпульс протона p, кінетична енергія котрого T = 500 МеВ.
|
Дано: T = 500 МеВ
|
|
p - ?
|
Розв’язання
З формул повної енергії релятивістської частинки (18.6) і (18.6а) маємо:
|
\(mc^{2}=\frac{m_{0}c^{2}}{\sqrt{1-\beta^{2}}}\), |
(1) |
де \(\beta=v/c\).
Після піднесення до квадрата виразу (1), одержимо
\(m^{2}c^{4}=\frac{m_{0}^{2}c^{4}}{1-\beta^{2}}\) \(\Rightarrow\) \(m^{2}c^{4}-m^{2}v^{2}c^{4}=m_{0}^{2}c^{4}\).
Врахувавши, що \(m_{0}c^{2}=E_{0}\) – енергія спокою (формула (18.6б)) і mv = p – релятивістський імпульс (формула (18.4а)), отримуємо:
|
\(E^{2}-p^{2}c^{2}=E_{0}^{2}\) \(\Rightarrow\) \(p=\frac{1}{c}\sqrt{E^{2}-E_{0}^{2}}\). |
(2) |
Повна енергія E дорівнює сумі кінетичної енергії T і енергії спокою E0:
E = E0 + T.
Підставивши цей вираз у формулу (2), знаходимо:
\(p=\frac{1}{c}\sqrt{T(T+2E_{0})}\).
З довідкових таблиць для протона \(E_{0}=938,3\) МеВ. Крім того використаємо зручну одиницю імпульсу ГеВ/с (див. задачу 18.6):
\(p=\frac{1}{c}\sqrt{500(500+2\cdot{938,3})}=1090\ \frac{МеВ}{c}=1,09\ \frac{ГеВ}{c}\)
В одиницях СІ:
p = 5,8·10-19 кг·м/с.
Задача 18.8
Визначити
роботу A, яку необхідно виконати, щоб змінити швидкість протона від v1 = 0,6c до v2 = 0,8c.
|
Дано: v1 = 0,6c
v2 = 0,8c
|
|
A - ?
|
Розв’язання
Виконана над частинкою робота дорівнює зміні її кінетичної енергії (рівняння (4.4). Кінетична енергія релятивістської частинки визначається виразом (18.9), отже
\(A=T_{2}-T_{1}=E_{0}\left(\frac{1}{\sqrt{1-\beta_{2}^{2}}}-1\right)- \left(\frac{1}{\sqrt{1-\beta_{1}^{2}}}-1\right)=E_{0}\left(\frac{1}{\sqrt{1-\beta_{2}^{2}}}-\frac{1}{\sqrt{1-\beta_{2}^{2}}}\right)\).
де \(\beta_{1}=v_{1}/c\), \(\beta_{2}=v_{2}/c\).
Підставивши в цей вираз числові значення v1 = 0,6c, v2 = 0,8c і табличне значення для протона E0 = 938,3 МеВ, одержимо
\(A=938,3\left(\frac{1}{\sqrt{1-0,64}}-\frac{1}{\sqrt{1-0,36}}\right)\approx{391}\) МеВ.
Задача 18.9
Енергія сонячного випромінювання, яке нормально падає щосекунди на одиничну площадку на поверхні Землі, дорівнює I = 1,4 кДж/(м2·с) (ця величина називається сонячною сталою і не враховує поглинання та розсіювання сонячного випромінювання атмосферою Землі). Прийнявши середній радіус земної орбіти R = 149,5·106 км і масу Сонця M = 2·1030 кг,
Визначити:
А) масу \(\mu\), що втрачає Сонце за одиницю часу;
Б) час t, за який маса Сонця зменшилася б на k = 1 % при незмінній інтенсивності випромінювання.
|
Дано: I = 1,4 кДж/(м2·с) = 1,4·103 Дж/(м2·с)
R = 149,5·106 км = 1,495·1011 м
M = 2·1030 кг
k = 1 %
|
|
\(\mu\) - ?
t - ?
|
Розв’язання
А) Зменшення маси Сонця відбувається внаслідок випромінювання енергії. Відповідно до співвідношення (18.7), шукана втрата маси
|
\(\mu=W/c^{2}\), |
(1) |
де W – енергія, що випромінюється Сонцем за 1 c по всіх напрямках.
Зрозуміло, що на площадку \(\Delta{S}\), що розташована на відстані R від Сонця, припадає частка цієї енергії, рівна
\(\Delta{W}=\frac{W}{4\pi{R}^{2}}\Delta{S}\).
Відповідно на одиницю площі за 1 c падає енергія
\(I=\frac{W}{4\pi{R}^{2}}\).
Підставивши цей вираз у формулу (1), одержимо шукану втрату маси:
\(\mu=\frac{W\cdot{4}\pi{R}^{2}}{c^{2}}=\frac{1,4\cdot{10}^{3}\cdot{4}\pi\cdot{(1,49\cdot{10}^{11})^{2}}}{(3\cdot{10}^{8})^{2}}\approx4,3\cdot{10}^{9}\) кг/с.
Б) Втрата маси Сонця за шуканий час за умовою становить
\(\Delta{m}=kM\).
З іншого боку \(\Delta{m}=\mu\cdot{t}\) (\(\mu\) – втрата маси за одиницю часу), отже
\(t=\frac{\Delta{m}}{\mu}=\frac{kM}{\mu}=\frac{0,01\cdot{2}\cdot{10}^{30}}{4,3\cdot{10}^{9}}=4,65\cdot{10}^{18}\) c,
що складає приблизно 150 мільярдів років.
Розділ 19. Квантові властивості випромінювання
|
Хвильові уявлення про природу світла є неповними. Вони не дозволяють пояснити явища, які безпосередньо пов'язані з процесами випускання і поглинання тілами електромагнітного випромінювання. Причина полягає в тому, що в дійсності випромінювання не є неперервною хвилею, тобто поширенням створюваних джерелом електромагнітних коливань у середовищі. Воно випускається і поглинається у вигляді мікроскопічних частинок, які називають фотонами або квантами. Особливістю фотонів є те, що в залежності від умов вони виявляють і властивості частинок - корпускулярні (слово "корпускула" означає "частинка") властивості, - і властивості хвиль. Така подвійність властивостей, або як говорять, "дуалізм" є універсальною властивістю матерії. Вона притаманна також і мікрочастинкам речовини, наприклад, електронам. Явища, у яких виявляються корпускулярні властивості світла, називаються квантовими оптичними ефектами. Теоретичні відомості |
19.1. Фотони та їхні характеристики
|
Світло випускається джерелом у вигляді потоку особливих мікроскопічних частинок, які називають фотонами (слово "фотон" можна перекласти з грецької мови як "частинка світла"). Фотону властиві як корпускулярні характеристики – енергія, маса, імпульс, – так і хвильові характеристики (частота і довжина хвилі), що пов'язані між собою. |
|
Енергія фотона E визначається за формулою Планка
де \(\nu\) – лінійна частота випромінювання. Величина
є універсальною фізичною сталою і називається сталою Планка. У теорії, як правило, користуються циклічною частотою \(\omega=2\pi\nu\) і записують формулу (19.1) у вигляді
де величина
теж називається сталою Планка (читається "аш перекреслене" або "аш з рискою"). Енергію фотона можна виразити і через довжину хвилі випромінювання у вакуумі \(\lambda\):
де c – швидкість світла у вакуумі. |
|
Маса фотона відповідно до формул (18.6), (19.1), (19.1a) і (19.1б) формально може бути введена як
або
Оскільки швидкість фотона дорівнює c, то, у відповідності до формули (18.5), маса спокою фотона \(\color{darkblue}{m_{0}=0}\). Це означає, що фотон не може існувати в стані спокою. Єдиний можливий стан фотона - це рух зі швидкістю c. Тому при зіткненні з іншими частинками можливе тільки або поглинання фотона, або відскок без втрати швидкості. |
|
Імпульс фотона, відповідно до формул (18.4а), (19.2) та (19.2а), виражається як
або
Енергія й імпульс фотона пов'язані співвідношенням
|
19.2. Фотоефект
|
Одним з доказів квантової природи випромінювання є фотоефект – явище, що широко використовується в різних галузях науки і техніки. Основним експериментальним методом дослідження фотоефекту є вимірювання вольт-амперних характеристик фотоефекту, які дозволяють визначити закономірності фотоефекту. Явище фотоефекту можна зрозуміти тільки виходячи з квантової теорії та рівняння Ейнштейна, яке пояснює закономірності зовнішнього фотоефекту. |
|
Фотоефектом називається вивільнення електронів речовини під дією електромагнітного випромінювання (світла). Вивільнені електрони в залежності від умов або залишаються усередині речовини, що опромінюється, або виходять за її межі. У першому випадку фотоефект називається внутрішнім, а в другому – зовнішнім. При опромінюванні світлом зовнішній фотоефект спостерігається тільки в металах. Тому часто говорять, що (зовнішнім) фотоефектом називається виривання електронів з металу під дією світла. Під дією рентгенівського або гама-випромінювання виривання електронів можливе і з діелектриків. Однак цей ефект прийнято називати екзоелектронною емісією. |
|
Властивості зовнішнього фотоефекту можна встановити, вивчаючи вплив умов опромінювання на вольт-амперні характеристики (ВАХ) вакуумного фотоелемента, тобто залежностей сили струму у фотоелементі від прикладеної напруги. Фотоелемент – це вакуумний діод - лампу, що має два електроди: катод і анод, катод якого опромінюється світлом. Тому він називається фотокатодом. Електричне коло для вимірювання ВАХ схематично показане на рис.19.1. За допомогою регульованого джерела напруги (РДН) між анодом А і фотокатодом ФК створюється напруга U необхідної величини та полярності. Напруга вимірюється вольтметром V. При опромінюванні фотокатода у фотоелементі з'являються вільні електрони (фотоелектрони), і в колі виникає струм, який вимірюється гальванометром (чутливим амперметром) Г.
Загальний вид ВАХ показаний на рис.19.2. Область \(U\ge{0}\) відповідає прямій полярності напруги (зазначена у верхній частині рис.19.2), а \(U<0\) – відповідає зворотній полярності напруги (див. там же). При U > 0 фотоелектрони притягаються до анода, а при U < 0 – відштовхуються від нього.
Характерними рисами ВАХ є: 1) насичення струму, тобто те, що при заданих умовах освітлення струм не може бути більшим за деяку величину Iн – струму насичення; 2) наявність струму при \(U\le{0}\). Насичення струму пояснюється тим, що електрони вириваються з фотокатода не електричним полем, а світлом. Тому їх кількість залежить не від напруги, а від умов опромінювання. Отже, для струму насичення можна записати:
де ne – кількість електронів, що вириваються світлом з фотокатода за одиницю часу, \(e=1,6\cdot{10}^{-19}\) Кл – елементарний заряд. Наявність струму при \(U\le{0}\) пов'язана з тим, що фотоелектрони вилітають з катода з деякою початковою швидкістю і, відповідно, кінетичною енергією. За рахунок цієї енергії частина фотоелектронів потрапляє на анод за відсутності, або навіть за невеликої зворотної напруги на фотоелементі. Найменша (за модулем) зворотна напруга Uз, при якій припиняється струм, називається затримуючою (або запірною) напругою. При U = Uз кінетична енергія навіть найшвидших фотоелектронів на шляху від катода до анода повністю витрачається на здійснення роботи (формула (10.12)) проти гальмуючого поля анода. Тому
де Uз – затримуюча напруга, e і m – модуль заряду та маса електрона, v – максимальна швидкість, з якою електрони вилітають з катода при заданих умовах опромінювання. |
|
Дослідження впливу умов опромінення на параметри Iн і Uз вольтамперних характеристик фотоелементів з катодами з різних металів з урахуванням співвідношень (19.5) і (19.6) призвели до встановлення таких загальних закономірностей зовнішнього фотоефекту: 1. Кількість фотоелектронів, що вириваються за одиницю часу, прямо пропорційна інтенсивності опромінюючого світла і не залежить від його частоти. 2. Максимальна кінетична енергія фотоелектронів лінійно залежить від частоти опромінюючого світла і не залежить від його інтенсивності. 3. Для кожного металу існує своя червона межа фотоефекту – мінімальна частота \(\nu_{0}\) (максимальна довжина хвилі \(\lambda_{0}\)) опромінюючого світла, при якій ще спостерігається фотоефект. Також було виявлено, що фотоефект практично безінерційний, тобто фотоелектрони з'являються майже відразу після початку опромінювання. Час затримки, тобто інтервал часу між початком опромінювання і виходом фотоелектронів, для зовнішнього фотоефекту складає \(\tau\sim{10}^{-9}\) с. |
|
Жодну із закономірностей фотоефекту неможливо пояснити на основі класичних уявлень. Наприклад, згідно з цими уявленнями електрони мали б виходити з металу за рахунок енергії вимушених коливань, створюваних змінним електричним полем світлової хвилі. Енергія вимушених коливань електронів прямо пропорційна квадрату амплітуди напруженості електричного поля світлової хвилі, тобто її інтенсивності. Тому кінетична енергія фотоелектронів повинна була б залежати від інтенсивності опромінюючого світла, чого насправді не спостерігається. Явище фотоефекту легко зрозуміти в рамках елементарної квантової теорії фотоефекту, створеної Ейнштейном. Відповідно до цієї теорії, у кожному елементарному акті фотоефекту
Для виходу за межі металу електрон повинен витратити певну мінімальну енергію, яка називається роботою виходу електрона A. Робота виходу залежить від індивідуальних властивостей металу і є його табличною характеристикою. Нагадаємо, що робота виходу вимірюється в "електрон-вольтах" (еВ). 1 еВ – енергія, якої набуває електрон, пройшовши прискорюючу різницю потенціалів 1 В: 1 еВ = 1,6·10-19 Дж. Тепер, на основі закону збереження енергії можна записати: W = E – A, де W – кінетична енергія електрона, що вилетів, E – енергія поглинутого фотона. Якщо в розглянутому співвідношенні врахувати вирази \(W=mv^{2}/2\) та \(E=h\nu\), то вийде рівняння Ейнштейна для зовнішнього фотоефекту:
Примітка 1. Під v розуміють максимальну швидкість виходу електронів при заданій частоті опромінюючого світла. Примітка 2. Для енергії фотона можна також використовувати вирази (19.1б) або (19.1а):
|
|
Рівняння Ейнштейна пояснює всі закономірності зовнішнього фотоефекту. По-перше, згідно квантового механізму, поглинання фотона електроном - це не процес, а подія. Цим пояснюється безінерційність фотоефекту. По-друге, безпосередньо з рівнянь (19.7) і (19.7б) випливає висновок про лінійну залежність кінетичної енергії фотоелектронів від частоти опромінюючого світла. По-третє, з рівнянь (19.7) і (19.7a) очевидно, що вихід електрона з металу можливий тільки за умови \(h\nu\ge{A}\) або \(hc/\lambda\ge{A}\), тобто при частоті світла
З цього видно, що кожному металу властива своя червона межа фотоефекту
Якщо напруга на фотоелементі дорівнює запірній U = Uз, то рівняння (19.7а) можна записати у вигляді
де Uз – запірна напруга, взята за абсолютним значенням. І останнє. Відповідно до квантових уявлень інтенсивність світла I (формула (15.11)) прямо пропорційна кількості фотонів, що падають на освітлювану поверхню протягом одиниці часу:
де E – енергія одного фотона, \(\Delta{S}_{\perp}\) – площа опромінюваної поверхні, розташованої перпендикулярно напрямку променів, \(\Delta{N}\) – кількість фотонів, що падають на поверхню \(\Delta{S}_{\perp}\) протягом часу \(\Delta{t}\), n – те ж саме за 1с. Очевидно, що кількість електронів ne, що вириваються світлом за одиницю часу, теж прямо пропорційна кількості n падаючих фотонів. Цим пояснюється прямо пропорційна залежність між ne і I (перша з закономірностей зовнішнього фотоефекту). |
19.3. Тиск світла
|
Тиск світла на опромінювану поверхню зумовлений ударами фотонів, подібно до того, як тиск газу зумовлений ударами молекул об стінки посудини. Він чисельно дорівнює нормальній складовій сумарного імпульсу, що передається підчас зіткнень одиниці площі стінки за одиницю часу. |
|
Для світла відмінність полягає в тому, що фотони зтикаються з опромінюваною поверхнею не тільки абсолютно пружно (при відбиванні світла), але й абсолютно непружно (при поглинанні світла). Кількості тих та інших фотонів визначаються коефіцієнтом відбивання R даної поверхні, тобто відношенням кількості відбитих фотонів до загальної кількості падаючих фотонів. Розрахунок дає таку загальну формулу світлового тиску P:
де I – інтенсивність падаючого світла, \(\alpha\) – кут падіння, c – швидкість світла, R – коефіцієнт відбивання – відношення числа відбитих фотонів до числа падаючих. При нормальному падінні (\(\alpha=0\))
Для ідеального дзеркала (R = 1)
Для абсолютно поглинаючої (чорної) поверхні (R = 0)
Таким чином, на дзеркальну поверхню світло здійснює більший тиск, ніж на чорну. Це було використано П.М. Лебедєвим для експериментального доказу існування тиску світла. |
Приклади розв'язування задач
|
При розв'язуванні задач на квантові властивості випромінювання необхідно згадати порядок організації розв'язування задач й оформлення розв'язку (див. "Етапи розв'язування задач"). |
Задачі цього розділу розділені на дві групи
Приклади розв'язування задач. Фотони (світлові кванти)
|
Задачі, в яких розглядаються характеристики фотонів, не вимагають будь-яких спеціальних порад. |
Задача 19.1. Визначити частоту \(\nu\) та довжину хвилі \(\lambda\) у вакуумі випромінювання, маса фотонів якого дорівнює масі електрона \(m_{e}=9,1\cdot{10}^{-31}\) кг.
Задача 19.2. У деякій речовині довжина хвилі світла становить \(\lambda=414\) нм при енергії фотонів E = 2,0 еВ (1 еВ = 1,6·10-19 Дж). Визначити показник заломлення n цієї речовини.
Задача 19.3. Лазер випромінює в імпульсі \(N=2\cdot{10}^{19}\) фотонів з довжиною хвилі \(\lambda=694\) нм. Визначити середню потужність випромінювання лазера P, якщо тривалість імпульсу \(\tau=2\) мс.
Задача 19.4. Лазер випромінює імпульси з енергією E = 10 Дж і тривалістю \(\tau=10\) мкс. Промінь від цього лазера, що нормально падає на дзеркальну поверхню, сфокусований в цятку діаметром d = 5 мкм. Визначити середній тиск P, що його створює лазерний імпульс на поверхню.
Задача 19.1
Визначити
частоту \(\nu\) та довжину хвилі \(\lambda\) у вакуумі випромінювання, маса фотонів якого дорівнює масі електрона \(m_{e}=9,1\cdot{10}^{-31}\) кг.
|
Дано: m = 9,1·10-31 кг
|
|
ν, λ - ?
|
Розв’язання
Відповідь дають формули (19.2) і (19.2a), згідно з якими
\(\nu=\frac{mc^{2}}{h}\), \(\lambda=\frac{h}{mc}\).
Підставивши задане значення m та табличні константи c = 3·108 м/с, h = 6,63·10-34 Дж·с, отримаємо:
\(\nu=\frac{9,1\cdot{10}^{-31}\cdot{9}\cdot{10}^{16}}{6,62\cdot{10}^{-34}}\approx{1,24}\cdot{10}^{20}\) Гц,
\(\lambda=\frac{6,63\cdot{10}^{-34}}{9,1\cdot{10}^{-31}\cdot{3}\cdot{10}^{8}}=2,42\cdot{10}^{-12}\) м = 2,42 пм.
Отримані числа відповідають найбільш високочастотній (короткохвилевій) ділянці електромагнітного спектра – гамма-випромінюванню.
Задача 19.2
У деякій речовині довжина хвилі світла становить \(\lambda=414\) нм при енергії фотонів E = 2,0 еВ (1 еВ = 1,6·10-19 Дж).
Визначити
показник заломлення n цієї речовини.
|
Дано: λ = 414 нм = 4,14·10-7 м
E = 2,0 еВ = 3,2·10-19 Дж
|
|
n - ?
|
Розв’язання
Енергія фотона визначає довжину світлової хвилі \(\lambda_{0}\) у вакуумі (формула (19.1б)):
|
|
\(E=\frac{hc}{\lambda_{0}}\) \(\Rightarrow\) \(\lambda_{0}=\frac{hc}{E}\). |
(1) |
У середовищі довжина світлової хвилі зменшується згідно з формулою (16.4), отже
\(n=\frac{\lambda_{0}}{\lambda}\).
Підставивши сюди вираз (1), дістанемо відповідь:
\(n=\frac{hc}{\lambda{e}}=\frac{6,63\cdot{10}^{-34}\cdot{3}\cdot{10}^{8}}{4,14\cdot{10}^{-7}\cdot{3,2}\cdot{10}^{-19}}\) = 1,5.
Задача 19.3
Лазер випромінює в імпульсі \(N=2\cdot{10}^{19}\) фотонів з довжиною хвилі \(\lambda=694\) нм.
Визначити
середню потужність випромінювання лазера P, якщо тривалість імпульсу \(\tau=2\) мс.
|
Дано: N = 2·1019
λ = 694 нм = 6,94·10-7 м
\(\tau=2\) мс = 2·10-3 с
|
|
P - ?
|
Розв’язання
Енергія одного фотона, випроміненого лазером (формула (19.1б)),
\(\varepsilon=\frac{hc}{\lambda}\),
де h = 6,63·10-34 Дж·с – стала Планка, с = 3·108 м/с – швидкість світла.
Загальна енергія лазерного імпульсу
\(W=N\varepsilon=N\frac{hc}{\lambda}\).
Середня потужність імпульсу
\(P=\frac{W}{\tau}=\frac{Nhc}{\tau\lambda}\).
Підставивши у цю формулу числові значення величин, одержимо відповідь:
\(P=2,86\cdot{10}^{-3}\) Вт = 2,86 мВт.
Задача 19.4
Лазер випромінює імпульси з енергією E = 10 Дж і тривалістю \(\tau=10\) мкс. Промінь від цього лазера, що нормально падає на дзеркальну поверхню, сфокусований в цятку діаметром d = 5 мкм.
Визначити
середній тиск P, що його створює лазерний імпульс на поверхню.
|
Дано: E = 10 Дж
τ = 10 мкс = 10-5 c
d = 5 мкм = 5·10-6 м
|
|
P - ?
|
Розв’язання
Згідно з умовою задачі шуканий тиск визначається формулою (19.10б):
|
|
\(P=\frac{2I}{c}\), |
(1) |
де I – середня інтенсивність лазерного імпульсу, c – швидкість світла.
Відповідно до означення (15.11)
\(I=\frac{E}{\tau{S}}\frac{4I}{\pi{d}^{2}\tau}\),
де \(S=\pi{d}^{2}/4\) – площа поверхні, на яку сфокусоване випромінювання.
Підставивши вираз I у формулу (1), дістанемо
\(P=\frac{8E}{\pi{c}d^{2}\tau}\).
Обчислення дають:
\(P=3,4\cdot{10}^{8}\) Па.
Отримана величина \(n\approx3000\) разів перевищує атмосферний тиск. Тому за допомогою сфокусованого лазерного променя можна робити отвори у найтвердіших матеріалах, а також використовувати його як «лазерний скальпель» у хірургії.
Приклади розв'язування задач. Фотоефект
|
У задачах на фотоефект треба мати на увазі, що робота виходу електрона (таблична величина) для всіх речовин \(A\le{10}\) еВ. Якщо енергія фотона значно перевищує це значення, то роботою виходу можна знехтувати. У таких випадках може виявитися необхідним застосування формул релятивістської механіки (теорії відносності). Це буває у випадках, коли енергія фотона співвимірна або більша за енергією спокою електрона (\(h\nu\gtrapprox{m}_{0}c^{2}\)). |
Задача 19.5. При опроміненні металу світлом кінетична енергія фотоелектронів виявилося W = 2,0 еВ (1 еВ = 1,6·10-19 Дж). Визначити частку енергії (k %) поглинутого фотона, яка витрачається на роботу виходу, якщо червона межа фотоефекту з цього металу \(\lambda=278\) нм.
Задача 19.6. При почерговому опроміненні катода фотоелемента світлом з довжинами хвилі \(\lambda\) і \(n\lambda\) виявилося, що затримуючі напруги відрізняються в n2 разів. Визначити довжину хвилі червоної межі фотоефекту \(\lambda_{0}\).
Задача 19.7. За певних умов опромінення катода струм у фотоелементі припиняється при зворотній напрузі Uз = 2 В. Визначити максимальну швидкість v, з якою електрони будуть потрапляти на анод, якщо до фотоелемента прикласти пряму напругу Uп = Uз.
Задача 19.8. До якого максимального потенціалу \(\varphi_{m}\) зарядиться віддалена від інших тіл мідна кулька при її опроміненні ультрафіолетовим світлом з довжиною хвилі \(\lambda=140\) нм? Робота виходу електронів з міді A = 4 еВ (1 еВ = 1,6·10-19 Дж).
Задача 19.9. Ультрафіолетове випромінювання з довжиною хвилі \(\lambda=232\) нм нормально падає на платинову пластинку (робота виходу A = 5,29 еВ). Вважаючи, що всі фотоелектрони вириваються з максимальною швидкістю і рухаються назустріч падаючим фотонам, визначити імпульс p, що його одержує пластинка при вильоті кожного електрона.
Задача 19.5
При опроміненні металу світлом кінетична енергія фотоелектронів виявилося W = 2,0 еВ (1 еВ = 1,6·10-19 Дж).
Визначити
частку енергії (k %) поглинутого фотона, яка витрачається на роботу виходу, якщо червона межа фотоефекту з цього металу \(\lambda=278\) нм.
|
Дано: W = 2,0 еВ = 3,2·10-19 Дж
\(\lambda=278\) нм
|
|
k - ?
|
Розв’язання
Енергія поглинутого фотона E розподіляється між роботою виходу A та кінетичною енергією фотоелектрона W у відповідності до закону збереження енергії: E = A + W.
Шукана частка енергії
|
\(k=\frac{A}{E}=\frac{A}{A+W}\) \(\Rightarrow\) \(k=\frac{1}{1+W/A}\). |
(1) |
Згідно з формулою (19.8а)
\(A=\frac{hc}{\lambda_{9}}\).
Підставивши це значення у вираз (1), дістанемо
\(k=\frac{1}{1+\lambda{W}/(hc)}\).
Підставивши сюди числові значення величин, отримаємо відповідь
k = 0,69 = 69 %.
Задача 19.6
При почерговому опроміненні катода фотоелемента світлом з довжинами хвилі \(\lambda\) і \(n\lambda\) виявилося, що затримуючі напруги відрізняються в n2 разів.
Визначити
довжину хвилі червоної межі фотоефекту \(\lambda_{0}\).
|
Дано: λ1 = λ
λ2 = nλ
U1/U2 = n2
|
|
λ0 - ?
|
Розв’язання
Енергія фотона та робота виходу визначаються через довжини хвиль опромінюючого світла та червоної межі фотоефекту виразами (19.1б) та (19.8a). Кінетична енергія фотоелектронів визначається затримуючою напругою згідно із співвідношенням (19.6). Тому рівняння Ейнштейна (19.7) для вказаних двох випадків опромінення набувають вигляду:
|
\(\frac{hc}{\lambda}=\frac{hc}{\lambda_{0}}+eU_{1}\), |
\(\Rightarrow\) |
\(hc\left(\frac{1}{\lambda}-\frac{1}{\lambda_{0}}\right)=eU_{1}\) |
(1) |
|
\(\frac{hc}{n\lambda}=\frac{hc}{\lambda_{0}}+e\frac{U_{1}}{n^{2}}\) |
\(hc\left(\frac{1}{n\lambda}-\frac{1}{\lambda_{0}}\right)=\frac{eU_{1}}{n^{2}}\). |
У другому рівнянні враховано, що при збільшенні довжини хвилі енергія фотона зменшується, тому затримуюча напруга також зменшується. Поділивши ліві та праві частини рівнянь (1), після нескладних викладок отримаємо:
\(\lambda_{0}=(n+1)\lambda\).
Задача 19.7
За певних умов опромінення катода струм у фотоелементі припиняється при зворотній напрузі Uз = 2 В.
Визначити
максимальну швидкість v, з якою електрони будуть потрапляти на анод, якщо до фотоелемента прикласти пряму напругу Uп = Uз.
|
Дано: Uз = 2 В
Uп = Uз
|
|
v - ?
|
Розв’язання
Згідно із законом збереження енергії кінетична енергія електрона при попаданні на анод
|
W = W0 +eUп, |
(1) |
де W0 – кінетична енергія електрона при виході з катода, eUп – робота поля, створюваного у фотоелементі прямою напругою Uп (e = 1,6·10-19 Кл – елементарний заряд).
Згідно з співвідношенням (19.6), максимальна кінетична енергія електрона при виході з катода
W0 = eUз.
Тоді з рівнянням (1) максимальна кінетична енергія електрона при попаданні на анод
\(W=\frac{mv^{2}}{2}=e(U_{з}+U_{п})\).
Оскільки за умовою Uп = Uз, то
\(\frac{mv^{2}}{2}=2eU_{з}\) \(\Rightarrow\) \(v=2\sqrt{\frac{eU_{з}}{m}}\).
Взявши з таблиць масу електрона m = 9,1·10-31 кг, отримаємо
\(v=2\sqrt{\frac{1,6\cdot{10}^{-19}\cdot{2}}{9,1\cdot{10}^{-31}}}\approx1,2\cdot{10}^{6}\) м/с.
Задача 19.8
До якого максимального потенціалу \(\varphi_{m}\) зарядиться віддалена від інших тіл мідна кулька при її опроміненні ультрафіолетовим світлом з довжиною хвилі \(\lambda=140\) нм? Робота виходу електронів з міді A = 4 еВ (1 еВ = 1,6·10-19 Дж).
|
Дано: λ = 140 нм = 1,4·10-7 м
A = 4 еВ = 6,4·10-19 Дж
|
|
φm - ?
|
Розв’язання
Внаслідок фотоефекту кулька втрачає електрони, отже заряджається позитивно (Нагадаємо, що первісно всі тіла є електрично-нейтральними, тобто алгебраїчна сума зарядів в тілі дорівнює нулю. Тому втрата заряду одного знаку означає набуття тілом такого ж заряду протилежного знаку). При цьому в міру втрати електронів потенціал кульки поступово зростає. Тому вирвані електрони рухаються в усе сильнішому гальмівному електричному полі. Через певний час після початку опромінення позитивний потенціал кульки стає таким, що всі вирвані випромінюванням електрони повертаються назад на кульку. Інакше кажучи, встановлюється динамічна рівновага: кількості електронів, що вириваються та повертаються, стають однаковими. Тому потенціал кульки перестає збільшуватися. Процес встановлення динамічної рівноваги відбувається дуже швидко – практично миттєво. Згідно з формулою (10.13) для подолання притягання кульки електрон має виконати роботу
|
\(A_{0}=e\varphi\), |
(1) |
де \(\varphi\) – потенціал кульки, \(e=1,6\cdot{10}^{-19}\) Кл – елементарний заряд. Цю роботу електрон виконує за рахунок кінетичної енергії W, яку отримує від опромінюючого світла. Отже максимальна робота, яку може виконати електрон
A0max = W,
і з виразу (1), максимальний потенціал кульки
|
\(\varphi=\frac{W}{e}\). |
(2) |
Згідно з рівнянням Ейнштейна (19.7а) кінетична енергія вильоту електрона з кульки
\(\frac{mv^{2}}{2}=W=\frac{hc}{\lambda}-A\).
Отже з виразу (2) максимальний потенціал кульки дорівнює
\(\varphi_{m}=\frac{hc}{\lambda{e}}-\frac{A}{e}\).
Після підстановки числових значень величин у цю формулу, обчислення дають:
\(\varphi=4,87\) В.
Задача 19.9
Ультрафіолетове випромінювання з довжиною хвилі \(\lambda=232\) нм нормально падає на платинову пластинку (робота виходу A = 5,29 еВ). Вважаючи, що всі фотоелектрони вириваються з максимальною швидкістю і рухаються назустріч падаючим фотонам,
визначити
імпульс p, що його одержує пластинка при вильоті кожного електрона.
|
Дано: λ = 232 нм = 2,32·10-7 м
A = 5,29 еВ
|
|
p - ?
|
Розв’язання
Пластинка одержує імпульс внаслідок двох процесів: поглинання фотона та вильоту електрона. При поглинанні фотона, пластинка отримує імпульс p1, рівний імпульсу фотона (формула (19.3a)):
|
\(p_{1}=\frac{h}{\lambda}\). |
(1) |
При вильоті електрона пластинка одержує імпульс віддачі p2, котрий за величиною дорівнює імпульсу електрона: p2 = pe Згідно з формулою (4.3б)
|
\(p_{e}=\sqrt{2mW}\), |
(2) |
де W – кінетична енергія, m – маса електрона.
Кінетична енергія електрона визначається з рівняння Ейнштейна для фотоефекту (19.7а):
|
\(W=\frac{mv^{2}}{2}=\frac{hc}{\lambda}-A\). |
|
Підставивши цей вираз у формулу (2), дістанемо:
|
\(p_{2}=p_{e}\sqrt{2m\left(\frac{hc}{\lambda}-A\right)}\). |
(3) |
Отже повний імпульс, що його отримує пластинка, відповідно до виразів (1) і (3) дорівнює:
\(p=p_{1}+p_{2}=\frac{h}{\lambda}+\sqrt{2m\left(\frac{hc}{\lambda}-A\right)}\).
Підставивши у цю формулу числові значення величин і вионавши обчислення, одержимо відповідь:
\(p=1,35\cdot{10}^{-25}\) кг·м/с.
Розділ 20. Будова атома
|
Речовина складається з молекул і атомів. Атомом називається найменша частка даного хімічного елемента, яка є носієм всіх його фізичних і хімічних властивостей. Слово "атом" походить від от грецького слова "атомос", тобто "неподільний". Але в дійсності атом являє собою систему зі складною внутрішньою будовою і властивостями. Будова і властивості атомів не можуть бути пояснені за допомогою законів класичної фізики. Теоретичною базою атомної фізики є квантова механіка. Теоретичні відомості Приклади розв’язування задач |
20.1. Ядерна модель атома
|
Те, що атом має певну внутрішню будову, стало очевидним після відкриття електрона – елементарної частинки, що входить до складу атома. Електрон має негативний електричний заряд \(e=-1,6\cdot{10}^{-19}\) Кл і масу \(m=9,1\cdot{10}^{-31}\) кг. Атоми в цілому електрично нейтральні. Це означає, що окрім електронів до складу атома входить позитивно заряджена речовина. Експерименти по визначенню розподілу маси і заряду позитивної речовини атома (досліди Резерфорда) призвели до відкриття атомного ядра. Атомне ядро - це "серцевина" атома, у якій зосереджений позитивний заряд і майже вся (~ 99,95 %) маса атома. Розміри ядра приблизно у 1000 раз менші за розміри атома і не перевищують величини \(10^{-14}\) м. Це означає, що електрони атома розташовуються поза межами ядра на дуже великих (у порівнянні з розмірами ядра) відстанях і перебувають у русі. Для того, щоб не впасти на ядро під дією кулонівської сили притягання, електрони повинні рухатися навколо нього. Швидкість цього так званого орбітального руху \(v\sim{10}^{6}\) м/с, а частота \(\nu\sim{10}^{14}~{с}^{-1}\). При такій частоті обертання заряд електронів нібито "розмазується" і утворює "електронну хмару" або електронну оболонку, що оточує ядро атома. Таким чином, атом складається з масивного позитивного ядра і негативної електронної оболонки, яка оточує це ядро. Тому розміри і більшість фізичних і хімічних властивостей атомів визначаються розмірами і будовою електронних оболонок. Зазначені уявлення про будову атома називають ядерною моделлю атома. |
20.2. Квантові постулати Бора
|
Ядерна модель атома спирається на незаперечні експериментальні факти. Однак вона несумісна з законами класичної фізики. Відповідно до електромагнітної теорії будь-яка заряджена частка, що рухається з прискоренням, неперервно випромінює енергію. Під час руху навколо ядра електрон має доцентрове прискорення і, отже, повинен неперервно втрачати енергію на випромінювання. Тому електрон в атомі мав би рухатися по спіралі, наближаючись до ядра, і зрештою впасти на нього. Але атоми є стійкими системами і можуть необмежено довго існувати без зміни властивостей. Тому ми вимушені констатувати, що підчас руху в атомі електрон не випромінює енергії. Ця обставина, а також невідповідність інших властивостей атомів законам класичної фізики спонукали видатного датського фізика, одного з творців квантової механіки Н. Бора, до формулювання так званих квантових постулатів Бора. Перший постулат Бора (постулат стаціонарних станів) стверджує:
Другий постулат Бора (правило частот) говорить, що
Поглинати енергію атоми теж можуть тільки дискретними порціями з енергіями (частотами), що задовольняють умовам (20.1) і (20.2). Хоча постулати Бора різко суперечать законам класичної фізики, вони відображують незаперечні дослідні факти: стійкість атомів і дискретний (квантовий) характер електромагнітного випромінювання. Дискретність квантових станів у атомі та правило частот пояснюють лінійчастий і виключно індивідуальний характер спектрів випромінювання і поглинання розріджених атомарних газів: атом кожного хімічного елемента має властивий тільки йому дискретний набір спектральних ліній. |
|||||||||
20.3. Атом Ґідрогену
Постулати Бора відіграли вирішальну роль у виникненні квантової фізики. Вони пояснили деякі властивості атома Гідрогену і дозволили теоретично розрахувати його енергетичні рівні, тобто всі можливі значення енергії стаціонарних станів, і оптичні спектри, тобто всі можливі частоти, що можуть випромінювати і поглинати атоми Гідрогену.
|
Енергетичні рівні атома Гідрогену визначаються формулою
де m, e – маса і заряд електрона, \(\hbar=1,05\cdot{10}^{-34}\) Дж×с – стала Планка, \(k=\frac{1}{4\pi\varepsilon_{0}}=9\cdot{10}^{9}\) м/Ф. Величина
Тому у числовому вигляді формула (20.3) записується так:
Натуральне число n називається головним квантовим числом. Його можна розглядати як номер даного енергетичного рівня у порядку зростання енергії.
З формули (20.3б) зрозуміло, що зі збільшенням n рівні енергії зближуються і при \(n\to\infty\) зливаються, прямуючи до значення \(E_{\infty}=0\). Це означає, що атом іонізується, тобто відбувається відривання електрона від ядра. Стан n = 1 з мінімальною енергією E1 = E0 (см. вираз (20.3а)) є стійким. У цьому стані атом може перебувати нескінченно довго, тому він називається основним станом. Перейти в будь-який інший стан атом може тільки одержавши енергію ззовні. Тому всі стани з n > 1 називаються збудженими. Збуджені стани нестабільні. Атом може перебувати в збудженому стані тільки протягом малого проміжку часу \(\tau\sim{10}^{-8}\) c, по чому спонтанно (самодовільно) переходить у який-небудь стан з меншою енергією, випромінюючи фотон. Таким чином, для того щоб атоми випромінювали енергію, їх потрібно весь час яким-небудь способом переводити у збуджені стани. Наприклад, у світних трубках, що використовуються у світловій рекламі, це робиться за допомогою газового розряду, тобто електричного струму. |
|
Оптичний спектр, тобто набір усіх можливих частот, що їх можуть випромінювати атоми Гідрогену, визначається узагальненою формулою Бальмера. Ця формула випливає з умови (20.2), формули (20.3) і має вигляд:
де n2 – номер рівня, з якого відбувається перехід, n1 – номер рівня, на який відбувається перехід електрона в атомі. Величина
називається сталою Рідберга. Всі частоти природно групуються у спектральні серії. Серія – це сукупність усіх частот (спектральних ліній), обумовлених переходами на заданий рівень n1. На рис.20.1 стрілками вказані переходи, що утворять перші три серії у спектрі атомарного Гідрогену. Формула (20.4) визначає також частоти світла, що можуть поглинати атоми Гідрогену. При цьому n2 – номер рівня на який переходить електрон, а n1 – номер рівня, з якого відбувається перехід. |
Приклади розв'язування задач
При розв'язуванні задач на атом Гідрогену треба врахувати наступне.
|
1) |
Якщо електрон перебуває у збудженому стані, то він може перейти на будь-який з більш низьких енергетичних рівнів. Якщо такий рівень не є першим (\(n\ne{1}\)), то електрон і надалі може переходити на нижчі рівні. Як наслідок, в спектрі випромінювання спостерігається сукупність спектральних ліній, частоти яких визначаються узагальненою формулою Бальмера (20.4). При цьому утворюються спектральні серії - групи ліній, які обумовлені переходами електрона на заданий нижчій рівень n1 з усіх вищих рівнів n2 = n1 +1, n1 +2,… |
|
|
|
|
2) |
Якщо електрон знаходився в стані з головним квантовим числом n1, то при поглинанні кванта енергії \(h\nu\) він перейде в стан з головним квантовим числом n2 за умови \(h\nu=E_{2}-E_{1}\), де E1, E2 – енергії, що відповідають головним квантовим числам n2 та n2. Строго кажучи, енергія фотона повинна бути дещо більшою, оскільки частина енергії та імпульсу фотона передається атому як цілому і надає йому деяку швидкість. Однак цей ефект незначний і в елементарній фізиці не враховується. |
|
|
|
|
3) |
Атом Гідрогену може переходити в збуджений стан у результаті зіткнення з іншими атомами. В такому випадку зберігається імпульс системи та її повна енергія (вона включає кінетичну енергію атомів, енергію електрона в атомі до і після зіткнення, а при необхідності й енергію фотона). |
Задача 20.1. Згідно з теорією Бора, електрон в атомі Гідрогену може рухатися тільки по таких колових орбітах, для яких добуток імпульсу електрона на довжину орбіти кратний сталій Планка: \(mv\cdot{2}\pi{r}=nh\), n = 1, 2, 3,… Виходячи з цього, визначити кутову швидкість електрона \(\omega\) на другій орбіті (n = 2).
Задача 20.2. У спектрі випромінювання атомарного Гідрогену при заданих умовах збудження спостерігається тільки три спектральні лінії. Визначити довжини хвиль цих ліній \(\lambda_{1}\), \(\lambda_{2}\), \(\lambda_{3}\).
Задача 20.3. Збуджені атоми Гідрогену знаходяться на n-ому енергетичному рівні. Визначити повну кількість ліній N, що спостерігаються у спектрі випромінювання цих атомів.
Задача 20.4. Електрон в нерухомому атомі Гідрогену знаходиться на енергетичному рівні n2 = 2. Визначити швидкість v руху атома після випромінювання фотона.
Задача 20.5. На нерухомий атом Гідрогену налітає інший атом Гідрогену. До зіткнення обидва атоми знаходилися в основному стані (n1 = 1). Визначити мінімальну кінетичну енергію W1, яку повинен мати рухомий атом, щоб при прямому непружному зіткненні один з атомів випустив фотон.
Задача 20.1
Згідно з теорією Бора, електрон в атомі Гідрогену може рухатися тільки по таких колових орбітах, для яких добуток імпульсу електрона на довжину орбіти кратний сталій Планка:
\(mv\cdot{2}\pi{r}=nh\), n = 1, 2, 3,…
Виходячи з цього,
визначити
кутову швидкість електрона \(\omega\) на другій орбіті (n = 2).
|
Дано: \(mv\cdot{2}\pi{r}=nh\)
n = 2
|
|
ω - ?
|
Розв’язання
В теорії Бора рух електрона в атомі Гідрогену навколо ядра розглядається як рух точкового заряду під дією кулонівської сили, яка створює доцентрове прискорення. Тому згідно з рівнянням (2.5) та формулами (10.3) і (2.17) можна записати
|
\(\frac{ke^{2}}{r^{2}}=m\omega{r}\) \(\Rightarrow\) \(ke^{2}=m\omega^{2}r^{3}\), |
(1) |
де \(\omega\) – шукана кутова швидкість електрона, \(m=9,1\cdot{10}^{-31}\) кг – його маса,
\(k=\frac{1}{4\pi\varepsilon_{0}}=9\cdot{10}^{9}\) м/Ф.
Крім того враховано, що заряди електрона та ядра атома Гідрогену по модулю рівні \(e=1,6\cdot{10}^{-19}\) Кл. Зробимо в заданій у тексті задачі умові стаціонарності заміни \(v=\omega\cdot{r}\), \(h=h/2\pi=\hbar\), і об’єднаємо її з рівнянням (1):
\(\left\{ \begin{matrix} n\hbar=m\omega{r}^{2} \\ m\omega^{2}r^{3}=ke^{2} \\ \end{matrix} \right.\).
Розв’язавши отриману систему відносно , дістанемо
\(\omega=\frac{k^{2}e^{4}m}{\hbar^{3}n^{3}}=\frac{(9\cdot{10}^{9})^{2}\dot(1,6\cdot{10}^{-19})^{4}\cdot{9,1}\cdot{10}^{-31}}{(1,05\cdot{10}^{-34})^{3}2^{3}}=5,2\cdot{10}^{15}\) c-1.
Задача 20.2
У спектрі випромінювання атомарного Гідрогену при заданих умовах збудження спостерігається тільки три спектральні лінії.
Визначити
довжини хвиль цих ліній \(\lambda_{1}\), \(\lambda_{2}\), \(\lambda_{3}\).
|
Дано: N = 3 |
|
λ1, λ2, λ3 - ?
|
Розв’язання
Згідно з квантовим механізмом випромінювання і умовою (20.1) атом Гідрогену випромінює фотон при переході електрона з будь-якого збудженого енергетичного рівня на будь-який з більш низьких рівнів.
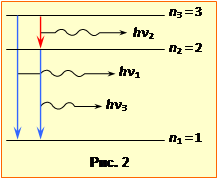 Якщо нижчий рівень сам є збудженим, то через короткий час (час життя збудженого стану) електрон знову переходить на один з більш низьких рівнів. Так продовжується, доки електрон не опиниться в основному стані. З наведених міркувань і схеми енергетичних рівнів (рис.2) неважко збагнути, що найвищий рівень, на якому знаходяться електрони в умовах задачі, відповідає головному квантовому числу n3 = 3. Тільки в цьому випадку можливі лише три переходи, показані стрілками на рис.2, і відповідно - три спектральні лінії з енергіями фотонів \(h\nu_{1}\), \(h\nu_{2}\), \(h\nu_{3}\). Частоти \(\nu_{1}\), \(\nu_{2}\), \(\nu_{3}\) визначаються формулою Бальмера (20.4). Врахувавши значення R = 3,29·1015 Гц, отримаємо
Якщо нижчий рівень сам є збудженим, то через короткий час (час життя збудженого стану) електрон знову переходить на один з більш низьких рівнів. Так продовжується, доки електрон не опиниться в основному стані. З наведених міркувань і схеми енергетичних рівнів (рис.2) неважко збагнути, що найвищий рівень, на якому знаходяться електрони в умовах задачі, відповідає головному квантовому числу n3 = 3. Тільки в цьому випадку можливі лише три переходи, показані стрілками на рис.2, і відповідно - три спектральні лінії з енергіями фотонів \(h\nu_{1}\), \(h\nu_{2}\), \(h\nu_{3}\). Частоти \(\nu_{1}\), \(\nu_{2}\), \(\nu_{3}\) визначаються формулою Бальмера (20.4). Врахувавши значення R = 3,29·1015 Гц, отримаємо
\(\nu_{1}=3,29\cdot{10}^{15}\left(1-\frac{1}{9}\right)=2,93\cdot{10}^{15}\) Гц,
\(\nu_{2}=3,29\cdot{10}^{15}\left(\frac{1}{4}-\frac{1}{9}\right)=4,58\cdot{10}^{14}\) Гц ,
\(\nu_{3}=3,29\cdot{10}^{15}\left(1-\frac{1}{4}\right)=2,47\cdot{10}^{15}\) Гц.
Довжини хвиль визначаються формулою (15.4a), отже
\(\lambda_{1}=\frac{c}{\nu_{1}}=\frac{3\cdot{10}^{8}}{2,93\cdot{10}^{15}}=102,7\) нм;
\(\lambda_{1}=\frac{c}{\nu_{1}}=\frac{3\cdot{10}^{8}}{4,58\cdot{10}^{14}}=656\) нм;
\(\lambda_{1}=\frac{c}{\nu_{1}}=\frac{3\cdot{10}^{8}}{2,47\cdot{10}^{15}}=121\) нм;
Задача 20.3
Збуджені атоми Гідрогену знаходяться на n-ому енергетичному рівні.
Визначити
повну кількість ліній N, що спостерігаються у спектрі випромінювання цих атомів.
|
Дано: n
|
|
N - ?
|
Розв’язання
 На рис. 3 схематично показані всі енергетичні рівні, на яких можуть перебувати електрони за умовою задачі.
На рис. 3 схематично показані всі енергетичні рівні, на яких можуть перебувати електрони за умовою задачі.
Відповідь на поставлене запитання можна отримати прямим підрахунком, взявши до уваги, що шукане число N дорівнює сумі кількостей всіх можливих переходів електронів на кожен з рівнів від першого до (n –1)-го. Очевидно, що таких можливих переходів є:
на перший рівень – n - 1,
на другий рівень – n – 2,
на третій рівень – n – 3,
………………………………………….
на (n - 1)-й рівень – 1.
Отримана числова послідовність є арифметичною прогресією з (n - 1) членів, причому a1 = n - 1, an-1 = 1. Сума арифметичної прогресії дорівнює добутку півсуми першого та останнього членів на їх кількість:
\(N=\frac{(n-1)+1}{2}(n-1)\) \(\Rightarrow\) \(N=\frac{n(n-1)}{2}\).
Примітка. Той, хто знає основи комбінаторики, може отримати відповідь коротше. У кожному переході беруть участь 2 з n рівнів. Тому кількість переходів дорівнює кількості комбінацій з n по 2:
\(N=C_{n}^{2}=\frac{n!}{2!{(n-2)!}}=\frac{(n-1)n}{2}\).
Задача 20.4
Електрон в нерухомому атомі Гідрогену знаходиться на енергетичному рівні n2 = 2.
Визначити
швидкість v руху атома після випромінювання фотона.
|
Дано: \(n_{2}=2\)
|
|
v - ?
|
Розв’язання
Фотон випромінюється при переході електрона зі збудженого рівня n2 = 2 на основний рівень n1 = 1. Енергія фотона W визначається співвідношенням (20.1) і формулою (20.3a):
|
\(W=E_{0}\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right)=\frac{3E_{0}}{4}\), |
(1) |
де E0 = 13,6 еВ.
Система атом – фотон є ізольованою, тому в ній зберігається імпульс. Оскільки до випромінювання імпульс системи дорівнював нулю, то
\(0=\vec{p}_{ф}+\vec{p}_{а}\) \(\Rightarrow\) \(\vec{p}_{а}=-\vec{p}_{ф}\),
де \(\vec{p}_{а}\), \(\vec{p}_{ф}\) – імпульси атома та випроміненого фотона. Таким чином, атом отримує імпульс "віддачі", рівний за величиною та протилежний за напрямком імпульсу фотона, що випромінюється. Імпульс фотона pф визначається через його енергію W співвідношенням (19.4):
\(p_{ф}=\frac{W}{c}\),
де c – швидкість світла.
В такому разі для модулів маємо:
\(\frac{W}{c}=mv_{а}\) \(\Rightarrow\) \(v=\frac{W}{m_{а}c}\),
де \(m_{а}=1,67\cdot{10}^{-27}\) кг – маса атома Гідрогену. Підставивши в цей вираз значення W з виразу (1), отримаємо
\(v=\frac{3E_{0}}{4m_{а}c}\).
Виразивши величину E0 = 13,6 еВ у джоулях і виконавши обчислення, дістанемо відповідь:
\(v=\frac{3\cdot{13,6}\cdot{1,6}\cdot{10}^{-19}}{4\cdot{1,67}\cdot{10}^{-27}\cdot{3}\cdot{10}^{8}}\approx\) 3,26 м/с.
Примітка. Внаслідок віддачі атом отримує не тільки імпульс, а й деяку кінетичну енергію Wа. Тому, строго говорячи, енергія фотона менша від значення (1) на величину Wа. Але підрахунок показує, що це абсолютно нехтовний ефект:
\(W_{а}=\frac{m_{а}v^{2}}{2}=8,87\cdot{10}^{27}\) Дж = \(5,5\cdot{10}^{-8}\) еВ.
В той же час енергія фотона
\(W=\frac{3\cdot{13,6}}{4}=10,2\) еВ.
Отже Wа << W.
Задача 20.5
На нерухомий атом Гідрогену налітає інший атом Гідрогену. До зіткнення обидва атоми знаходилися в основному стані (n1 = 1).
Визначити
мінімальну кінетичну енергію W1, яку повинен мати рухомий атом, щоб при прямому непружному зіткненні один з атомів випустив фотон.
|
Дано: n1 = 1
|
|
W1 - ?
|
Розв’язання
Зіткнення атомів відбувається з виконанням законів збереження енергії та імпульсу. При непружному зіткненні частина кінетичної енергії налітаючого атома перетворюється на внутрішню енергію, що означає перехід одного або двох атомів у збуджений стан. Мінімальна необхідна енергія очевидно відповідає переходу одного атома з основного стану (n1 = 1) у перший збуджений (n2 = 2). При зворотному переході цей атом випускає фотон.
За законом збереження енергії
|
\(W_{1}=W_{2}+\Delta{W}\), |
(1) |
де W1 – кінетична енергія атома, що налітає, W2 – кінетична енергія атомів після непружного зіткнення, \(\Delta{W}\) – зміна внутрішньої енергії, тобто енергія збудження.
Згідно виразами (20.1) і (20.3a)
|
\(\Delta{W}=E_{0}\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right)\). |
(2) |
За законом збереження імпульсу
|
\(p_{1}=p_{2}\), |
(3) |
де p1 – імпульс атома, що налітає, p2 – імпульс атомів після непружного удару.
Імпульс і кінетична енергія зв'язані співвідношенням (4.3б)
\(W=\frac{p^{2}}{2m}\) \(\Rightarrow\) \(p=\sqrt{2mW}\).
Тому вираз (3) можна записати у вигляді
|
\(\sqrt{2mW_{1}}=\sqrt{2\cdot{2}nW_{2}}\) \(\Rightarrow\) \(W_{1}=2W_{2}\), |
(4) |
де враховано, що після непружного удару атоми рухаються разом, як одна частинка з масою 2m (m – маса одного атома). З огляду на вирази (2) і (4), формула (1) набуває вигляду
\(W_{1}=\frac{W_{1}}{2}+E_{0}\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right)\) \(\Rightarrow\) \(W_{1}=E_{0}\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right)\).
Підставивши сюди значення E0 = 13,6 еВ, n1 = 1, n2 = 2, дістанемо:
\(W_{1}=2\cdot13,6\cdot\left(1-\frac{1}{4}\right)\) = 20,4 еВ.
Розділ 21. Атомне ядро
|
Не тільки атом, але й атомне ядро має складну будову та особливі властивості. Визначальними рисами ядер є їхня велика міцність і здатність ядер одних хімічних елементів перетворюватися на ядра інших елементів. Такі перетворення можуть відбуватися як спонтанно, так і під дією інших частинок. ("Спонтанно" означає "самодовільно", тобто без зовнішнього впливу.) Перетворення атомних ядер супроводжуються радіоактивним випромінюванням - потоками різних елементарних частинок, яким властива сильна біологічна дія. Деякі ядерні процеси супроводжуються виділенням великої кількості енергії. Це використовується для практичного одержання енергії. Наприклад, значну частку електричної енергії отримують на атомних електростанціях (АЕС). |
21.1. Склад атомного ядра
|
До складу атомного ядра входять масивні елементарні частинки двох видів, які називають загальним терміном нуклони. Загальна кількість нуклонів і співвідношення між кількостями нуклонів кожного виду визначають характеристики і властивості ядер, зокрема, - існування ізотопів. |
|
Існує два види нуклонів - протони і нейтрони. (Термін "нуклон" перекладається як "ядерна частинка) Протон – це позитивно заряджена елементарна частинка, що має електричний заряд і масу спокою (нагадаємо, що 1 а.о.м. = \(1,66\cdot{10}^{-27}\) кг). Відношення мас спокою протона й електрона \(m_{p}/m_{e}\approx{1836}\). Протон є найпростішим ядром – ядром атома звичайного Гідрогену. (термін "протон" у перекладі означає "найпростіший"). Нейтрон – це електрично нейтральна частинка. Маса спокою нейтрона \(m_{n}=1,00867\) а.о.м. (відношення мас спокою нейтрона й електрона \(m_{n}/m_{e}\approx{1839}\). |
|
Найважливішими характеристиками атомного ядра є електричний заряд і маса. Заряд ядра qя визначається визначається кількістю протонів, що входять до складу ядра і описується зарядовим числом ядра Z:
де \(e=1,6\cdot{10}^{-19}\) Кл – елементарний заряд. Зарядове число визначає також кількість електронів у нейтральному атомі, від якої залежать його хімічні властивості та положення даного елемента в періодичній системі Д.І. Менделєєва:
Маси нуклонів (в а.о.м.) близькі до 1, тому округлена маса ядра в а.о.м. чисельно дорівнює загальній кількості нуклонів. Загальна кількість нуклонів A, що входять до складу ядра, називається масовим числом ядра. Оскільки маса атома практично збігається з масою ядра, то масові числа ядер визначають і відносні атомні маси елементів, що також вказані в періодичній таблиці хімічних елементів. Число нейтронів N у ядрі
У ядерній фізиці використовують умовні позначення ядер, що включають символ хімічного елемента X, масове A і зарядове Z число ядра: \({}_{Z}^{A}\mathrm{X}\). Наприклад: Гелій \({}_{2}^{4}\mathrm{He}\), Нітроген \({}_{7}^{14}\mathrm{N}\) тощо. У літературі можна зустріти і таке позначення: \({}_{Z}X^{A}\) Так само роблять і з елементарними частинками. Наприклад: протон \({}_{1}^{1}{p}\), нейтрон \({}_{1}^{0}{n}\), електрон \({}_{-1}^{0}{e}\) та ін. (Оскільки протон – це ядро Гідрогену, тому для нього використовують також позначення \({}_{1}^{1}\mathrm{H}\)). |
|
Складною будовою атомного ядра пояснюється існування ізотопів. Ізотопами називаються різновиди атомів одного й того ж хімічного елемента, які відрізняються за масою. Ядра ізотопів хімічного елемента складаються з однакової кількості протонів і займають те ж саме місце у періодичній системі елементів, але відрізняються за кількістю нейтронів N і загальною кількістю нуклонів A. (термін "ізотоп" перекладається як "той, що займає те ж саме місце) Усі хімічні елементи мають ізотопи. Ізотопи одного елемента мають однакові хімічні і дуже близькі фізичні властивості. У ядерній фізиці для розрізнення ядер використовують термін "нуклід". Нуклід – це ядро (або сукупність ядер) із заданими значеннями масового і зарядового чисел, тобто із заданою кількістю протонів і нейтронів. Термін "нуклід" використовують і як синонім терміна "ізотоп". |
21.2. Енергія зв'язку атомного ядра
|
Нуклони в ядрі утримуються специфічними ядерними силами. Міцність ядра характеризується енергією зв'язку атомного ядра, яку можна визначити за відповідними формулами розрахунку енергії зв'язку. Зчеплення між нуклонами характеризується питомою енергією зв'язку нуклонів. |
|
Ядерні сили є проявом так званої сильної взаємодії. Сильна взаємодія – це фундаментальна взаємодія, тобто вона не зводиться ні до яким іншої. Ядерні сили мають різноманітні і складні властивості. Вкажемо тільки на деякі з них: 1. Ядерні сили є "найсильнішими" з усіх відомих сил. Зокрема, сили ядерного зчеплення між нуклонами в ядрі набагато переважають сили електричного відштовхування між протонами. 2. Ядерні сили є "зарядосиметричними" - вони не залежать від наявності або відсутності у частинок електричного заряду. 3. Ядерні сили є короткодіючими. Вони виявляються тільки на відстанях \(r\le{10}^{-15}\) м, тобто діють лише всередині атомного ядра. 4. Ядерні сили мають властивість насичення. Це означає, що кожен нуклон у ядрі може взаємодіяти тільки з обмеженою кількістю інших нуклонів. Останні дві властивості ядерних сил принципово відмінні від електромагнітних. Електромагнітні сили є дальнодіючими і не насичуються. Це означає, що у системі електрично заряджених частинок кожна з них взаємодіє з усіма іншими незалежно від кількості частинок і розмірів системи. |
|
Енергією зв'язку атомного ядра називається мінімальна енергія, яку необхідно витратити, щоб розділити ядро на окремі не взаємодіючі між собою нуклони. (Поняття енергії зв'язку стосується не тільки ядра, але й інших зв'язаних систем. Наприклад, енергія дисоціації молекули є не що інше, як енергія зв'язку). Енергія зв'язку є мірою міцності атомного ядра: чим міцніше ядро, тим більша енергія необхідна для його "руйнування" на окремі нуклони. Ядерні сили настільки великі, що в ядерних процесах стає помітним взаємозв'язок між масою та енергією (формула (18.6)). Це дозволяє розрахувати енергію зв'язку будь-якого атомного ядра за точними значеннями мас нуклонів і ядра. Відповідно до закону збереження енергії для гіпотетичного процесу поділу ядра на нуклони має місце очевидний енергетичний баланс:
де \(E_{я}\) – енергія спокою ядра, \(E_{зв}\) – енергія зв'язку, \(E_{нукл}\) – сумарна енергія спокою вільних нуклонів, що утворилися. Так як \(E_{нукл}>E_{я}\), то відповідно до закону Ейнштейна (формула (18.6)), сумарна маса нуклонів, що входять до складу ядра, більше за масу самого ядра. Цей висновок цілком підтверджується результатами точних вимірювань мас нуклідів за допомогою приладу, який називається мас-спектрометром . Підставивши в рівняння (21.3) співвідношення \(E=mc^{2}\), одержимо
де величина
називається дефектом маси ядра. У даному значенні цей термін використовується в елементарній фізиці. У ядерній фізиці дефектом маси називають іншу, але близьку за змістом, величину. |
|
З виразів (21.5) і (21.4) легко одержати розрахункові формули для енергії зв'язку ядра. Очевидно, що сумарна маса нуклонів, що входять у задане ядро
де Z – зарядове число ядра (кількість протонів), A – масове число (загальна кількість нуклонів), mp і mn – маси вільних протона і нейтрона. З урахуванням виразів (21.5) і (21.6) формула (21.4) набуває вигляду
У довідкових таблицях наводяться не маси ядер, а маси нейтральних атомів. Тому замість формули (21.7) використовують модифіковану формулу
де \(m_{н}\) – маса нейтрального атома Гідрогену \({}_{1}^{1}\mathrm{H}\) – маса нейтрального атома розглянутого ізотопу. У ядерній фізиці масу визначають в а.о.м (1 а.о.м. = 1,66\(\cdot{10}^{-27}\) кг), а енергію – в мегаелектронвольтах (МеВ) (1 МеВ = 106 еВ = \(1,6\cdot{10}^{-13}\) Дж). При цьому масі m1 = 1 а.о.м. відповідає енергія (енергетичний еквівалент) \(E_{1}=m_{1}c^{2}=931,5\) МеВ. Тому для практичних розрахунків замість формули (21.7а) зручно використовувати числову формулу
в якій маси виражені в а.о.м. |
|
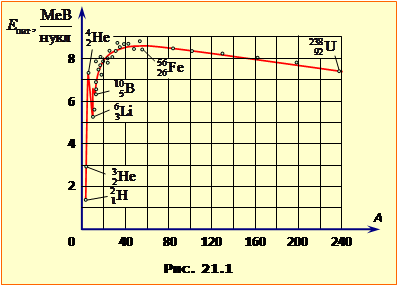
Зчеплення (зв'язок) окремого нуклона з усіма іншими нуклонами в ядрі характеризується усередненою величиною, що називається питомою енергією зв'язку нуклонів. Питома енергія зв'язку нуклонів \(E_{пит}\) – це відношення енергії зв'язку ядра \(E_{зв}\) до загальної кількості нуклонів A:
Величина Eпит складно залежить від багатьох факторів і не може бути виражена формулою, але існує чітка закономірність, показана умовним графіком на рис.21.1 (графік є умовним у тому сенсі, що масові числа ядер не формують безперервну послідовність). При збільшенні кількості нуклонів у ядрі A питома енергія \(E_{пит}\) спочатку різко зростає, досягаючи максимуму 8,8 МеВ/нукл при \(A=40\sim{50}\), а потім повільно монотонно спадає до \(\approx{7,6}\) Мев/нукл для нуклідів, розташованих у кінці періодичної системи (\(A=240\sim{250}\)).
Зростання \(E_{пит}\) на початковій ділянці пояснюється збільшенням кількості партнерів, з якими взаємодіє кожен нуклон у ядрі. Подальший хід залежності \(E_{пит}(A)\) пов'язаний із властивістю насичення ядерних сил. При значенні \(A\approx{40}\) кожний нуклон у ядрі вже має максимально можливу кількість партнерів, з якими може взаємодіяти. Тому подальше збільшення A ніяк не впливає на питому енергію ядерної взаємодії нуклонів. Однак між протонами діють сили електричного відштовхування, які послаблюють зчеплення між протонами і, відповідно, зменшують питому енергію зв'язку. Для електричних сил ефект насичення відсутній, тому зменшення питомої енергії зв'язку спостерігається до самого кінця періодичної системи. З цим же зв'язана і закономірна зміна співвідношення між кількістю нейтронів N і кількістю протонів Z при збільшенні загальної кількості нуклонів A, що показано умовним графіком на рис.21.2.
Відношення N/Z поступово збільшується від значення 1, типового для легких нуклідів, до значення 1,6 наприкінці періодичної системи. Ядра поступово нібито "розбавляються" нейтронами. Це призводить до збільшення відстані між протонами та послабленню електричного відштовхування між ними, а отже, й до підвищення міцності ядра. |
21.3. Природна радіоактивність
|
Хоча в цілому атомні ядра дуже міцні, у природі існують нестійкі нукліди. Ядра деяких ізотопів одних хімічних елементів спонтанно (самодовільно, без зовнішнього впливу) перетворюються на ядра інших елементів. Ця властивість називається природною радіоактивністю, а самі такі нукліди – радіоактивними ізотопами. Процес перетворення одних ядер на інші називається радіоактивним розпадом. Радіоактивні ядра випускають декілька видів радіоактивного випромінювання. Відповідно, існують різні види і схеми радіоактивного розпаду. Унаслідок розпаду кількість будь-якого радіоактивного нукліду безупинно зменшується відповідно до закону радіоактивного розпаду. |
|
У випадку природної радіоактивності спостерігається три види радіоактивного випромінювання: \(\alpha-\), \(\beta-\) і \(\gamma-\)випромінювання. \(\color{green}{\mathbf{\alpha-}}\)випромінювання – це потік \(\alpha-\)частинок, що являють собою ядра нукліду Гелію \({}_{2}^{4}\mathrm{He}\). Таким чином, \(\alpha-\)частинка має позитивний електричний заряд \(q_{\alpha}=Ze=3,2\cdot{10}^{-19}\) Кл і масу \(m_{\alpha}=4,00260\) а.о.м. (точніше, це маса нейтрального атома) \(\color{green}{\mathbf{\beta-}}\)випромінювання – це потік \(\beta-\)частинок, які являють собою не що інше, як електрони. Тому \(\beta-\)частинки позначають ще, як \(e^{-}\) або \({}_{-1}^{0}e\). \(\color{green}{\gamma-}\)випромінювання – дуже жорстке електромагнітне випромінювання, яке є потоком \(\gamma-\)квантів, тобто фотонів з дуже великою енергією (> 105 еВ) і дуже малою довжиною хвилі (\(<5\cdot{10}^{-12}\) м). Кінетичні енергії \(\alpha-\), \(\beta-\)частинок і енергія \(\gamma-\)квантів дуже великі. Тому радіоактивному випромінюванню властива сильна біологічна дія, і воно небезпечне для життя. Особливо це стосується \(\gamma-\)випромінювання, що має високу проникаючу здатність. Висока проникаюча здатність \(\gamma-\)випромінювання пояснюється тим, що \(\gamma-\)кванти (фотони) є нейтральними частинками. |
|
Відповідно до видів і назв частинок, що випускаються, розрізняють види і схеми радіоактивного розпаду. Перетворення ядер з випромінюванням \(\alpha-\)частинок називається \(\alpha-\)розпадом, а з випромінюванням \(\beta-\)частинок – \(\beta-\)розпадом. Ядерні процеси, як і будь-які інші, підпорядковані універсальним законам збереження імпульсу, енергії, електричного заряду. Крім того існує ще низка специфічних законів збереження, що діють у світі елементарних частинок. Зокрема, це закон збереження кількості нуклонів, відповідно до якого при різних перетвореннях ядер загальна кількість нуклонів не змінюється. Закони збереження заряду і кількості нуклонів означають, що
Цим визначаються схеми \(\alpha-\) і \(\beta-\)розпаду заданого нукліда X з утворенням нового нукліда Y: 1. \(\alpha-\)розпад:
1. \(\beta-\)розпад:
Зарядове і масове числа нукліда Y, що утворюється, визначається зазначеними законами збереження. Зарядове число ядра визначає місце елемента в періодичній системі. Тому зі схем (21.9) і (21.10) випливають так звані правила зміщення:
Як при \(\alpha-\)розпаді, так і при \(\beta-\)розпаді ядро, що утворилося звичайно перебуває в збудженому стані. Переходячи в основний стан, воно випускає один або декілька \(\gamma-\)квантів. Тому обидва види розпаду супроводжуються \(\gamma-\)випромінюванням. При \(\beta-\)розпаді випускається ще одна частинка, яка називається антинейтрино. Але в задачах елементарної фізики це не враховується. |
|
З часом кількість радіоактивного нукліда зменшується відповідно до закону радіоактивного розпаду:
де N – кількість радіоактивних ядер, що не розпалися на даний момент часу t, N0 – їх кількість у момент початку відліку, e = 2,718… – основа натуральних логарифмів. Коефіцієнт \(\lambda\) (1/с) називається сталою розпаду, яка є індивідуальною характеристикою кожного радіоактивного нукліду. Замість \(\lambda\) часто використовують обернену величину
яка називається тривалістю життя нукліду. З урахуванням виразу (21.12) закон радіоактивного розпаду записується так:
Величина \(\tau\) має простий зміст. При \(t=\tau\)
тобто можна сказати, що тривалість життя – це проміжок часу протягом якого кількість радіоактивних ядер зменшується в \(e\approx{2,72}\) рази. (див. рис.21.3). На практиці швидкість розпаду радіоактивного нукліду характеризують періодом піврозпаду T – проміжком часу, протягом якого розпадається половина вихідної кількості радіоактивного нукліду (див. рис.21.3) Період піврозпаду T пов'язаний з тривалістю життя співвідношенням
Закон розпаду через T записується у вигляді
|
21.4. Ядерні реакції
|
Перетворення атомних ядер відбуваються не тільки самодовільно підчас радіоактивного розпаду, але й вимушено в різних ядерних реакціях, тобто в результаті взаємодії ядра з елементарними частинками або іншими ядрами. Ядерні реакції супроводжуються виділенням або поглинанням енергії і характеризуються енергетичним виходом реакції, для визначення якого використовують відповідні формули розрахунку. До реакцій, в яких виділяється велика кількість енергії, належать реакція поділу важких ядер і реакція синтезу легких ядер. |
|
Оскільки ядерні сили дуже великі, в ядерних реакціях спостерігається помітна зміна маси спокою частинок, що беруть участь у реакції. Це означає, що відбувається помітне перетворення енергії спокою в інші види енергії, або навпаки. При цьому повна енергія зберігається: \(E_{п1}=E_{п2}\), де \(E_{п1}\) – повна енергія вихідних учасників реакції, \(E_{п2}\) – повна енергія продуктів реакції. Повна енергія частинки \(E_{п}\) дорівнює сумі енергії спокою E і кінетичної енергії Eк. Тому можна записати:
Строго кажучи, в енергетичний баланс входить і енергія електромагнітного випромінювання (\(\gamma\)-випромінювання), яким супроводжується реакція. Але ця енергія порівняно незначна, і нею можна знехтувати. Величина
називається енергетичним виходом ядерної реакції. З рівняння (21.16) випливає, що енергетичний вихід дорівнює різниці початкової і кінцевої енергій спокою системи:
або відповідно до формули (18.6 б),
де \(\Delta{m}=m_{1}-m_{2}\) – "дефект маси" реакції. При \(\Delta{m}>0\) (маса спокою в результаті зменшується) \(Q>0\) і реакція відбувається з виділенням енергії. Якщо ж \(\Delta{m}<0\) (маса спокою збільшується), то реакція супроводжується поглинанням енергії. |
|
При відомих точних значеннях мас усіх вихідних учасників і продуктів реакції формулою розрахунку енергетичного виходу є вираз (21.17а). Але енергетичний вихід можна розрахувати і через енергію зв'язку. Відповідно до співвідношення (21.3), для енергії спокою системи E та енергетичного виходу реакції Q можна записати:
Загальна кількість нуклонів, а отже їхня енергія спокою, у ядерних процесах зберігаються: Eн1 = Eн2. Тому
Отже,
Зокрема, якщо енергія зв'язку в результаті реакції збільшується, то така реакція відбувається з виділенням енергії. |
|
Однією з ядерних реакцій, підчас якої виділяється енергія, є реакція поділу масивних ядер. Нехай, наприклад, ядро із загальною кількістю нуклонів A1 розщеплюється на два однакових "осколки поділу", тобто на два інших ядра з A2 = A1/2 кожне. Тоді початкове і кінцеве значення енергії зв'язку системи можна виразити як \(E_{зв1}=A_{1}E_{пит1}\) і \(E_{зв2}=2A_{2}E_{пит2}=A_{1}E_{пит2}\), де \(E_{пит1}\), \(E_{пит2}\) – питомі енергії зв'язку нуклонів у вихідному ядрі та ядрах – продуктах розпаду. Відповідно до формули (21.18) енергетичний вихід \(Q=A_{1}(E_{пит2}- E_{пит1})\). Оскільки \(E_{пит2}> E_{пит1}\) (див. рис.21.1), то \(Q>0\), тобто енергія виділяється. Якщо взяти A1 = 240, то Eпит1 \(\approx{7,6}\) МеВ/нукл і. Тоді \(Q\approx{220}\) МеВ/ядро. (На практиці використовують розпад ядер урану \({}^{235}\mathrm{U}\) і плутонію \({}^{239}\mathrm{Pu}\). При цьому енергія, що виділяється трохи менша: \(\approx{200}\) МеВ/ядро. Це пов'язано з тим, що ймовірність розпаду ядра на осколки однакової маси порівняно невелика, і реальна зміна енергії зв'язку буде в середньому менше, ніж прийнято в даному розрахунку). Енергія, що виділяється при поділі ядер величезна. Для порівняння, підчас хімічної реакції горіння на кожен атом реагуючих речовин виділяється у \(\sim{10}^{8}\) менша енергія. |
|
Іншим типом реакцій з виділенням енергії є реакції синтезу легких ядер, тобто злиття двох легких ядер з утворенням більш масивного ядра. Прикладом може слугувати реакція синтезу важких ізотопів Гідрогену – дейтерію \({}_{1}^{2}\mathrm{H}\) і тритію \({}_{1}^{3}\mathrm{H}\) – з утворенням гелію і нейтрона: \({}_{1}^{2}\mathrm{H}+{}_{1}^{3}\mathrm{H}\longrightarrow{}_{2}^{4}\mathrm{He}+{}_{0}^{1}n\). У цій реакції виділяється енергія 17,6 МеВ що в перерахунку на один нуклон набагато більше, ніж у реакціях розпаду. Для здійснення реакції синтезу вихідні ядра повинні наблизиться "впритул" так щоб між ними почали діяти ядерні сили зчеплення. Але для цього ядра повинні мати дуже велику кінетичну енергію, достатню для подолання кулонівского відштовхування між ними. Необхідна енергія відповідає температурі \(\sim{10}^{8}\) К Тому реакції синтезу ядер називають термоядерними реакціями. Досягнення і підтримка таких температур являє собою дуже складну технічну проблему. У даний час проблема керованої термоядерної реакції поки що не розв'язана. Технічно реалізована тільки некерована вибухова реакція цього типу. |
Склад ядра; енергія зв'язку
|
При розв'язуванні задач на склад ядра кількість протонів визначається з періодичної таблиці елементів (таблиці Д.І. Менделєєва) за порядковим номером елемента. Якщо в умові задачі на обчислення енергії зв'язку ядра не вказані точні значення мас необхідних частинок і нуклідів, їх беруть з довідкових таблиць. Увага! У таких розрахунках неприпустиме округлення вихідних даних. Необхідно використовувати всі значущі цифри, зазначені в довідкових даних. Необхідно також звертати увагу на те, що саме подано в довідковій таблиці: маси ядер чи маси нейтральних атомів. У першому випадку для розрахунку використовується формула (21.7), а в другому – (21.7a) або (21.7б). |
Задача 21.1. Визначити питому енергію зв'язку Eпит нуклонів в ядрах \({}_{3}^{7}\mathrm{Li}\), \({}_{27}^{58}\mathrm{Co}\), \({}_{92}^{235}\mathrm{U}\) за заданими масами протона, нейтрона та нейтральних атомів.
Задача 21.2. Визначити енергію зв'язку ядра, яке має однакову кількість протонів і нейтронів, а його радіус у k = 1,5 разів менший, ніж у ядра \({}^{27}\mathrm{Al}\). Вважати середню густину ядерної речовини однаковою для всіх ядер.
Задача 21.1
Визначити
питому енергію зв'язку Eпит нуклонів в ядрах \({}_{3}^{7}\mathrm{Li}\), \({}_{27}^{58}\mathrm{Co}\), \({}_{92}^{235}\mathrm{U}\) за заданими масами протона, нейтрона та нейтральних атомів:
mp = 1,00728 а.о.м.,
mn = 1,00867 а.о.м.,
mLi = 7,01601 а.о.м.,
mCo = 57,93575 а.о.м.,
mU = 235,04394 а.о.м.
Розв’язання
Питома енергія зв'язку нуклонів визначається співвідношенням (21.8):
\(E_{пит}=\frac{E_{зв}}{A}\),
де \(E_{зв}\) – енергія зв'язку ядра, A – число нуклонів в ядрі, рівне масовому числу ізотопа.
Маси задані в а.о.м. тому для енергії зв'язку \(E_{зв}\) зручно використати формулу (21.7б).
Згідно з заданими величинами обчислюємо:
\({}_{3}^{7}\mathrm{Li}\): \(E_{зв}=\frac{3\cdot{1,00728}+4\cdot{1,00867}-7,01601}{7}\cdot{931,5}=5,36\) МеВ/нукл;
\({}_{27}^{58}\mathrm{Co}\): \( E_{зв}=\frac{27\cdot{1,00728}+31\cdot{1,00867}-57,93575}{58}\cdot{931,5}=8,51\) МеВ/нукл;
\({}_{92}^{235}\mathrm{U}\): \( E_{зв}=\frac{92\cdot{1,00728}+143\cdot{1,00867}-235,04394}{235}\cdot{931,5}=7,39\) МеВ/нукл;
Задача 21.2
Визначити
енергію зв'язку ядра, яке має однакову кількість протонів і нейтронів, а його радіус у k = 1,5 разів менший, ніж у ядра \({}^{27}\mathrm{Al}\). Вважати середню густину ядерної речовини однаковою для всіх ядер.
Маси:
протона mp = 1,00867 а.о.м.,
нейтрона mn = 1,00728 а.о.м.,
ядра \({}^{27}\mathrm{Al}\) mAl = 26,96661 а.о.м.
|
Дано: k = 1,5
mAl = 26,96661 а.о.м.
|
|
\(E_{зв}\) - ?
|
Розв’язання
З урахуванням рівності кількості протонів і нейтронів (Z = N A – Z), формула (21.7 б) для енергії зв'язку ядра набуває вигляду:
|
\(E_{зв}=(N(m_{p}+m_{n})-m)\cdot{931,5}\), |
(1) |
де mp, mn, m – маса протона, нейтрона і ядра, виражена в а.о.м.
Таким чином, розв'язування задачі зводиться до визначення m і N. Обидві величини знайдемо з умови незмінності середньої густини ядерної речовини \(\rho=m/V\) (V – об'єм ядра):
|
\(\frac{m}{V}=\frac{m_{Al}}{V_{Al}}\) \(\Rightarrow\) \(\frac{m}{m_{Al}}=\frac{V}{V_{Al}}\). |
(2) |
Будемо вважати ядра кулями, тоді \(V=\frac{4}{3}\pi{R}^{3}\) і \(V_{Al}=\frac{4}{3}\pi{(kR)^{3}}\). Врахувавши, що за умовою k = 3/2, із співвідношення (2) отримуємо:
|
\(m=\frac{8}{27}m_{Al}\). |
(3) |
Маса ядра приблизно дорівнює добутку маси одного нуклона mн на їх кількість у ядрі A. Тому m = 2Nmн, mAl = 27mн (27 – масове число для \({}^{27}\mathrm{Al}\)). Підставивши ці значення у вираз (2), знаходимо
\(2Nm_{н}=\frac{8}{27}27m_{н}\) \(\Rightarrow\) N = 4.
Знайдені значення N і m (формула (3)) підставляємо у формулу (1) і остаточно одержуємо:
\(E_{зв}=\left(4(m_{p}+m_{n})-\frac{8}{27}m_{Al}\right)\cdot{931,5}\).
Виконаємо обчислення:
\(E_{зв}=\left(4(1,00728+1,00867)-\frac{8}{27}\cdot{26,96661}\right)\cdot{931,5}=68,6\) МеВ.
Ядерні реакції
|
У задачах на ядерні реакції звичайно потрібно визначити ("розшифрувати") якусь невідому частинку, що бере участь у реакції і розрахувати енергетичний вихід реакції. Іноді завдання включає визначення швидкостей частинок - учасників реакції. 1. Для визначення "невідомого" учасника реакції слід скласти баланси масових і зарядових чисел, тобто прирівняти суми зазначених чисел у лівій і правій частинах реакції. Після цього знаходять A і Z шуканої частинки. 2. Методика розрахунку енергетичного виходу визначається наведеною в тексті задачі довідковою інформацією. Якщо вказані точні значення мас частинок, то використовується формула (21.17a). Якщо задані енергії зв'язку ядер або питомі енергії зв'язку нуклонів, то розрахунок виконується за формулою (21.18). У цих обчисленнях неприпустиме округлення вихідних цифрових даних і проміжних результатів 3. Для визначення величини і напрямку руху зазначених у завданні частинок використовується рівняння енергетичного балансу реакції (21.16) і рівняння балансу імпульсів (див. розділ 3 ("Закон збереження імпульсу"), формули (3.3) і (3.4)). |
Задача 21.3. У приведених нижче рівняннях ядерних реакцій:
а) \({}_{13}^{27}\mathrm{Al}+{}_{0}^{1}n\to{X}+ {}_{2}^{4}\mathrm{He}\);
б) \({}_{6}^{12}\mathrm{C}+{X}\to{}_{6}^{13}\mathrm{C}\);
в) \({}_{25}^{56}\mathrm{Mn}\to\mathrm{X}+{}_{-1}^{0}e\).
Визначити не вказані частинки X.
Задача 21.4. За допомогою табличних значень мас ядер нуклідів та протона й нейтрона
|
mLi = 7,01601 |
|
mBe = 7,01693 |
|
mO = 15,99491 |
|
mH = 2,01410 |
|
mHe = 4,00260 |
|
mN = 14,00307 |
|
mp = 1,00728 |
|
mn = 1,00867 |
(маси подані в а.о.м.). Визначити енергію Q наступних реакцій:
1) \({}_{3}^{7}\mathrm{Li}+{}_{1}^{1}p\to{}_{0}^{1}n+{}_{4}^{7}\mathrm{Be}\);
2) \({}_{8}^{16}\mathrm{O}+{}_{1}^{2}\mathrm{H}\to{}_{2}^{4}\mathrm{He}+{}_{7}^{14}\mathrm{N}\)
Задача 21.5. Вважаючи, що в одному акті поділу ядра \({}^{235}\mathrm{U}\) вивільняється енергія E = 200 МеВ, визначити: А) енергію W, що виділяється при поділі mU = 1 кг урану \({}^{235}\mathrm{U}\); Б) масу m кам'яного вугілля з теплотворною здатністю q = 30 МДж/кг яка еквівалентна в тепловому відношенні одному кілограму \({}^{235}\mathrm{U}\).
Задача 21.6. З ядер дейтерію (\({}^{2}\mathrm{H}\)) утворився гелій \({}^{4}\mathrm{He}\) масою mHe = 1 г. Визначити: А) енергію Q, що при цьому виділилася; Б) масу m кам'яного вугілля з теплотворною здатністю q = 30 МДж/кг, яку потрібно спалити для одержання такої ж кількості теплової енергії.
Задача 21.7. При бомбардуванні ядер Нітрогену \(\alpha-\)частинками (ядра гелію \({}_{2}^{4}\mathrm{He}\)) утворюються ядра Оксигену та протони:
\({}_{7}^{14}\mathrm{N}+{}_{2}^{4}\mathrm{He}\to{}_{1}^{2}p+{}_{8}^{17}\mathrm{O}\)
Визначити енергетичний вихід Q реакції, якщо кінетична енергія \(\alpha-\)частинки, що налітає, \(T_{\alpha}=4,0\) МеВ, а утворений протон вилітає під кутом \(\theta=60^{\circ}\) до напрямку руху \(\alpha-\)частинки і має кінетичну енергію Tp = 2,09 МеВ.
Задача 21.3
У приведених нижче рівняннях ядерних реакцій:
а) \({}_{13}^{27}\mathrm{Al}+{}_{0}^{1}n\to{X}+ {}_{2}^{4}\mathrm{He}\);
б) \({}_{6}^{12}\mathrm{C}+{X}\to{}_{6}^{13}\mathrm{C}\);
в) \({}_{25}^{56}\mathrm{Mn}\to\mathrm{X}+{}_{-1}^{0}e\).
Визначити
не вказані частинки X.
Розв’язання
У будь-якій ядерній реакції зберігаються зарядове Z і масове A числа:
\(\sum\limits_{i}Z_{ni}=\sum\limits_{i}Z_{ki}\), \(\sum\limits_{i}Z_{ni}=\sum\limits_{i}A_{ki}\),
де індекс "n" відповідає початковому значенню, "k" – кінцевому. Виконавши відповідні підрахунки для заданих реакцій, знаходимо:
|
а) \({}_{13}^{27}\mathrm{Al}+{}_{0}^{1}n\to{X}+ {}_{2}^{4}\mathrm{He}\) |
\({}_{11}^{24}\mathrm{X}={}_{11}^{24}\mathrm{Na}\) |
|
|
б) \({}_{6}^{12}\mathrm{C}+{X}\to{}_{6}^{13}\mathrm{C}\) |
\({}_{0}^{1}\mathrm{X}={}_{0}^{1}n\) |
|
|
в) \({}_{25}^{56}\mathrm{Mn}\to\mathrm{X}+{}_{-1}^{0}e\) |
\({}_{26}^{56}\mathrm{X}={}_{26}^{56}\mathrm{Fe}\) |
Задача 21.4
За допомогою табличних значень мас ядер нуклідів та протона й нейтрона
|
mLi = 7,01601 |
|
mBe = 7,01693 |
|
mO = 15,99491 |
|
mH = 2,01410 |
|
mHe = 4,00260 |
|
mN = 14,00307 |
|
mp = 1,00728 |
|
mn = 1,00867 |
(маси подані в а.о.м.)
Визначити
енергію Q наступних реакцій:
1) \({}_{3}^{7}\mathrm{Li}+{}_{1}^{1}p\to{}_{0}^{1}n+{}_{4}^{7}\mathrm{Be}\);
2) \({}_{8}^{16}\mathrm{O}+{}_{1}^{2}\mathrm{H}\to{}_{2}^{4}\mathrm{He}+{}_{7}^{14}\mathrm{N}\)
Розв’язання
Згідно з наведеними числовим даними, енергетичний вихід ядерної реакції слід визначати за формулою (21.7a), враховуючи при цьому енергетичний еквівалент \(c^{2}\cdot{1}\) а.о.м. = 931,5 МеВ
\(Q=\Delta{m}\cdot{931,5}\) МеВб
де \(\Delta{m}=m_{1}-m_{2}\) – різниця сумарних мас вихідних та кінцевих ділянок учасників реакції.
Для реакції 1)
Q = ((7,01601 + 1,00728) – (1,00867 + 7,01693))·931,5 = -1,64 МеВ.
Знак "–" свідчить про те, що дана реакція йде з поглинанням енергії (ендотермічна реакція), тобто вихідним продуктам необхідно надавати енергію, щоб дана реакція стала можлива. Звичайно кінетичну енергію надають більш легким частинкам (тут це протон), розганяючи їх в прискорювачах.
Для випадку 2)
Q = ((15,99491 + 2,01410) – (4,0026 + 14,00307)·931,5 = 3,11 МеВ.
В цій реакції енергія виділяється, і її називають екзотермічною реакцією.
Задача 21.5
Вважаючи, що в одному акті поділу ядра \({}^{235}\mathrm{U}\) вивільняється енергія E = 200 МеВ,
визначити:
А) енергію W, що виділяється при поділі mU = 1 кг урану \({}^{235}\mathrm{U}\);
Б) масу m кам'яного вугілля з теплотворною здатністю q = 30 МДж/кг яка еквівалентна в тепловому відношенні одному кілограму \({}^{235}\mathrm{U}\).
|
Дано: \({}^{235}\mathrm{U}\)
E = 200 МеВ
mU = 1 кг
q = 30 МДж/кг
|
|
W - ?
m - ?
|
Розв’язання
Енергія, що виділяється при поділі одного кілограма урану дорівнює
|
W = N·E, |
(1) |
де N – кількість атомів, що розпалися.
Число N знайдемо на підставі виразів (7.3) і (7.6):
|
\(\nu=\frac{m_{U}}{M}=\frac{N}{N_{0}}\) \(\Rightarrow\) \(N=\frac{m_{U}}{M}N_{0}\), |
(2) |
де \(M=235\cdot{10}^{-3}\) кг/моль – атомна маса урану, \(N_{0}=6,02\cdot{10}^{23}\) 1/моль – стала Авагадро. Підставивши значення N (формула (2)) у вираз (1), одержимо:
\(W=\frac{m_{U}}{M}N_{0}\cdot{E}=\frac{1}{235\cdot{10}^{-3}}\cdot{6,02}\cdot{10}^{23}\cdot{200}=5,12\cdot{10}^{26}\) МеВ = \(8,2\cdot{10}^{13}\) Дж.
При згорянні вугілля маси m виділяється кількість тепла (формула (8.18))
Q = qm \(\Rightarrow\) \(m=\frac{Q}{q}\).
За умовою енергії, що виділяються, однакові Q = W, тому еквівалентна маса вугілля
\(m=\frac{W}{q}=\frac{8,2\cdot{10}^{13}}{30\cdot{10}^{6}}=2,37\cdot{10}^{6}\) кг = 2733 т.
Задача 21.6
З ядер дейтерію (\({}^{2}\mathrm{H}\)) утворився гелій \({}^{4}\mathrm{He}\) масою mHe = 1 г.
Визначити:
А) енергію Q, що при цьому виділилася;
Б) масу m кам'яного вугілля з теплотворною здатністю q = 30 МДж/кг, яку потрібно спалити для одержання такої ж кількості теплової енергії.
|
Дано: 2H
4H
mHe = 1 г
q = 30 МДж/кг
|
|
Q - ?
m - ?
|
Розв’язання
Реакція утворення більш важких нуклідів з легких називається реакцією синтезу. Схема цієї реакції має вигляд:
\({}_{1}^{2}\mathrm{H}+{}_{1}^{2}\mathrm{H}\to{}_{2}^{4}\mathrm{He}\).
Енергія реакції дорівнює
E = (2mH - mHe)·931,5 МеВ,
де mH = 2,01410 а.о.м. – маса ядра дейтерію, mHe = 4,0026 а.о.м. – маса ядра гелію.
Виконаємо обчислення
E = (2·2,01410 – 4,00260)·931,5 = 23,846 МеВ.
В одному грамі гелію міститься кількість атомів (дивись формули (7.3), (7.6))
\(N=\frac{m_{\mathrm{He}}}{M}N_{0}=\frac{10^{-3}}{3\cdot{10}^{-3}}\cdot{10}^{23}=1,505\cdot{10}^{23}\),
тому загальна енергія, що виділилася, складає
\(Q=E\cdot{N}=3,59\cdot{10}^{24}\) МеВ =\(5,74\cdot{10}^{11}\) Дж.
Для одержання такої ж енергії з вугілля, необхідно спалити масу вугілля
\(m=\frac{Q}{q}=\frac{5,74\cdot{10}^{11}}{3\cdot{10}^{7}}=19140\) кг = 19,14 т.
Зауваження. Якщо порівняти результати цієї і попередньої задач, то стане очевидно, що термоядерна реакція (реакція синтезу) у багато разів ефективніша, ніж реакція поділу урану.
Задача 21.7
При бомбардуванні ядер Нітрогену \(\alpha-\)частинками (ядра гелію \({}_{2}^{4}\mathrm{He}\)) утворюються ядра Оксигену та протони:
\({}_{7}^{14}\mathrm{N}+{}_{2}^{4}\mathrm{He}\to{}_{1}^{2}p+{}_{8}^{17}\mathrm{O}\)
Визначити
енергетичний вихід Q реакції, якщо кінетична енергія \(\alpha-\)частинки, що налітає, \(T_{\alpha}=4,0\) МеВ, а утворений протон вилітає під кутом \(\theta=60^{\circ}\) до напрямку руху \(\alpha-\)частинки і має кінетичну енергію Tp = 2,09 МеВ.
|
Дано: Tα = 4,0 МеВ
θ = 60°
Tp = 2,09 МеВ
|
|
Q - ?
|
Розв’язання
Енергетичний вихід ядерної реакції можна визначити як різницю сумарної кінетичної енергії частинок, що утворилися в реакції, і сумарної кінетичної енергії вихідних ядер (формула (21.16а)):
|
Q = (Tp + TO) – (TN + \(T_{\alpha}\)) = Tp + TO - \(T_{\alpha}\). |
(1) |
Тут враховано, що ядро Нітрогену до реакції перебувало у спокої.
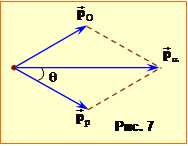
Таким чином, для отримання відповіді необхідно визначити кінетичну енергію ядра \({}^{17}\mathrm{O}\). Для цього скористаємося законом збереження імпульсу:
|
\(\vec{p}_{\alpha}=\vec{p}_{p}+\vec{p}_{O}\), |
(2) |
де \(\vec{p}_{\alpha}\), \(\vec{p}_{p}\), \(\vec{p}_{O}\) – вектори імпульсу відповідно \(\alpha-\)частинки, протона і Оксигену. Векторному рівнянню (2) відповідає діаграма імпульсів на рис.7. З неї очевидно, що модуль вектора \(\vec{p}_{O}\) легко визначити за теоремою косинусів:
\(p_{O}^{2}=p_{\alpha}^{2}-2p_{p}p_{\alpha}\cos\theta\).
Модуль імпульсу і кінетична енергія T зв'язані співвідношенням \(p^{2}=2mT\) (див. формулу (4.3б)), тому
\(2m_{O}T_{O}=2m_{p}T_{p}-4\sqrt{m_{\alpha}m_{p}T_{\alpha}T_{p}}\cos\theta\).
Звідси
\(T_{0}=\eta_{p}T_{p}+\eta_{\alpha}T_{\alpha}-2\sqrt{\eta_{\alpha}\eta_{p} T_{\alpha} T_{p}}\cos\theta\),
де введені позначення \(\eta_{p}=\frac{m_{p}}{m_{O}}=5,9287\cdot{10}^{-2}\), \(\eta_{\alpha}=\frac{m_{\alpha}}{m_{O}}\) = 0,23546.
Підставивши вираз TO в формулу (1), знаходимо
\(Q=(1+\eta)T_{p}-(1-\eta_{\alpha})T_{\alpha}-2\sqrt{\eta_{\alpha}\eta_{p}T_{\alpha}T_{p}}\cos\theta=-1,2\) МеВ.
Закон радіоактивного розпаду
|
При розв'язуванні задач на закон радіоактивного розпаду необхідно бути уважним в операціях зі степенями: множення - ділення і логарифмування - потенціювання. |
Задача 21.8. В урановій руді відношення кількості ядер \({}^{238}\mathrm{U}\) до кількості ядер \({}^{206}\mathrm{Pb}\) складає \(\eta=2,8\). Оцінити вік \(\tau\) уранової руди. Період піврозпаду \({}^{238}\mathrm{U}\) \(T_{1/2}=4,5\cdot{10}^{9}\) років. Вважати, що весь Плюмбум \({}^{206}\mathrm{Pb}\) є кінцевим продуктом розпаду урану.
Задача 21.9. У калориметр вмістили \(\beta-\)радіоактивний препарат \({}^{24}\mathrm{Na}\) масою m = 1 мг. Період піврозпаду препарату T = 15 годин. Оцінити кількість тепла Q, що виділяється в калориметрі за добу. Вважати, що всі частинки мають кінетичну енергію, рівну \(\eta=1/3\) максимально можливої в цій реакції.
Задача 21.8
В урановій руді відношення кількості ядер \({}^{238}\mathrm{U}\) до кількості ядер \({}^{206}\mathrm{Pb}\) складає \(\eta=2,8\).
Оцінити
вік \(\tau\) уранової руди.
Період піврозпаду \({}^{238}\mathrm{U}\) \(T_{1/2}=4,5\cdot{10}^{9}\) років. Вважати, що весь Плюмбум \({}^{206}\mathrm{Pb}\) є кінцевим продуктом розпаду урану.
|
Дано: η = 2,8
T1/2 = 4,5·109 років
|
|
\(\tau\) - ?
|
Розв’язання
Число радіоактивних ядер, що не розпалися на момент часу \(\tau\), визначається законом радіоактивного розпаду (21.11):
NU = \(N_{0}e^{-\lambda\tau}\)
де N0 – число вихідних ядер, \(\lambda\) – стала розпаду.
Із співвідношень (21.12) і (21.14) випливає, що
\(\lambda=\frac{\ln{2}}{T}\).
Тоді можна записати:
|
\(N_{U}=N_{0}e^{-\frac{\tau\ln{2}}{T}}=N_{0}\cdot{2}^{-\frac{\tau}{T}}\). |
(1) |
Число ядер, що розпалися, яке дорівнює числу ядер свинцю Pb, що утворилися:
|
NPb = \(N_{0}-N=N_{0}(1-2^{-\frac{\tau}{T}})\). |
(2) |
Розділивши вирази (1) на (2), одержимо:
|
\(\eta=\frac{N_{\mathrm{U}}}{ N_{\mathrm{Pb}}}=\frac{1}{2^{-\frac{\tau}{T}}-1}\) \(\Rightarrow\) \(2^{\frac{\tau}{T}}=\frac{\eta+1}{\eta}\). |
|
Із цього виразу після логарифмування отримуємо
\(\tau=T\cdot{}\frac{\ln\frac{\eta+1}{\eta}}{\ln{2}}\approx2\cdot{10}^{9}\) років.
Задача 21.9
У калориметр вмістили \(\beta-\)радіоактивний препарат \({}^{24}\mathrm{Na}\) масою m = 1 мг. Період піврозпаду препарату T = 15 годин
Оцінити
кількість тепла Q, що виділяється в калориметрі за добу. Вважати, що всі частинки мають кінетичну енергію, рівну \(\eta=1/3\) максимально можливої в цій реакції.
Енергія зв'язку: ядра \({}^{24}\mathrm{Na}\) E1 = 193,5 МеВ ядра \({}^{24}\mathrm{Mg}\) E2 = 198,3 МеВ.
|
Дано: m = 1 мг = 10-6 кг
T = 15 годин
η = 1/3
E1 = 193,5 МеВ
E2 = 198,3 МеВ
|
|
Q - ?
|
Розв’язання
Згідно з виразом (21.10) реакція \(\beta-\)розпаду \({}^{24}\mathrm{Na}\) має вигляд
\({}_{11}^{24}\mathrm{Na}\to{}_{12}^{24}\mathrm{Mg}+{}_{-1}^{0}e\).
Енергетичний вихід реакції Q1 через енергії зв'язку визначається формулою (21.18):
\(Q_{1}=E_{2}-E_{1}=4,8\) MeВ.
В реакції \(\beta-\)розпаду крім електрона \({}_{-1}^{0}e\) утворюється ще одна елементарна частинка – антинейтрино, яка не показана в схемі реакції (21.10). Антинейтрино відносить енергію, що може мати величину від 0 і аж до \(Q_{1}\). Тому \(Q_{1}\) є максимально можливою енергією електрона, а її середнє значення набагато менше і, згідно з умовою, становить
\(Q^{\prime}=Q/3=1,6\) МеВ = \(2,56\cdot{10}^{-13}\) Дж.
Кінетичну енергію ядра \({}^{24}\mathrm{Mg}\) можна не брати до уваги. Справді, згідно з законом збереження імпульсу, імпульси ядра \({}^{24}\mathrm{Mg}\) та електрона за величиною однакові. Тому відношення їх кінетичних енергій (формула (4.3б)
\(T_{я}/T_{e}=m_{e}/m_{я}=0,00055/24=2\cdot{10}^{-5}\).
Загальна енергія, що виділяється в калориметрі, дорівнює енергії \(Q^{\prime}\), помноженій на кількість ядер \(N^{\prime}\), що розпалися:
|
\(Q=Q^{\prime}N^{\prime}\). |
(1) |
Відповідно до закону розпаду (21.15) число ядер, що розпалися \(N^{\prime}=N-N_{0}\), визначається виразом:
|
\(N^{\prime}=N_{0}\left(1-e^{-\lambda\tau}\right)=N_{0}\left(1-2^{-\frac{\tau}{T}}\right)\). |
(2) |
Кількість ядер \({}^{24}\mathrm{Na}\) у початковий момент \(N_{0}\) знаходимо згідно з основними положеннями молекулярно-кінетичної теорії (формули (7.3) і (7.6)):
|
\(N_{0}\frac{m}{M}N_{A}\), |
(3) |
де \(M=24\cdot{10}^{-3}\) кг/моль – молярна маса ізотопу \({}^{24}\mathrm{Na}\), \(N_{A}=6,02\cdot{10}^{23}\) 1/моль – стала Авогадро.
Підставивши значення (3) у вираз (2), а його – у формулу (1), дістанемо:
\(Q=Q^{\prime}N^{\prime}=Q^{\prime}\frac{m}{M}N_{A}\left(1-2^{-\frac{\tau}{T}}\right)\) =
=\(2,56\cdot{10}^{-13}\cdot\frac{10^{-6}}{24\cdot{10}^{-3}}\cdot{6,02}\cdot{10}^{23}\left(1-2^{-\frac{24}{15}}\right)=4,3\cdot{10}^{6}\) Дж \(\approx{4,3}\) МДж.
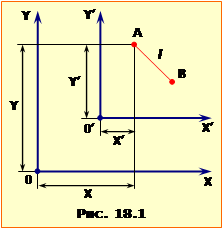
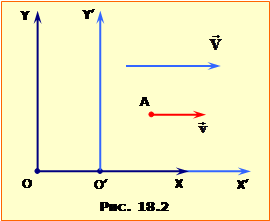 В механіці СТВ зв′язок між швидкостями тіла у двох різних системах відліку досить складний і не може бути виражений у загальній векторній формі. Тому розглянемо окремий випадок, показаний на рис.18.2.
В механіці СТВ зв′язок між швидкостями тіла у двох різних системах відліку досить складний і не може бути виражений у загальній векторній формі. Тому розглянемо окремий випадок, показаний на рис.18.2.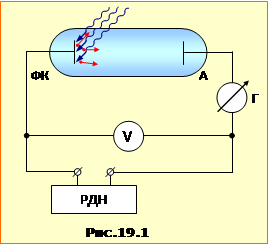
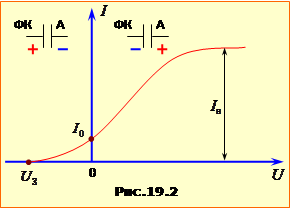
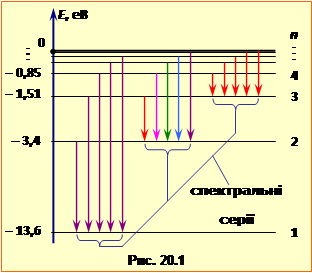 Схема розташування енергетичних рівнів атома Гідрогену показана горизонтальними лініями на рис.20.1. Для більшої наочності пропорції на рис. 20.1 дещо змінені.
Схема розташування енергетичних рівнів атома Гідрогену показана горизонтальними лініями на рис.20.1. Для більшої наочності пропорції на рис. 20.1 дещо змінені.