ФІЗИКА. Вчимося розв'язувати задачі. "МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА". Компенсаційний курс
| Site: | physics.zfftt.kpi.ua |
| Course: | physics.zfftt.kpi.ua |
| Book: | ФІЗИКА. Вчимося розв'язувати задачі. "МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА". Компенсаційний курс |
| Printed by: | |
| Date: | Wednesday, 4 March 2026, 1:26 PM |
Table of contents
- ВСТУП
- Розділ І. Ідеальний газ
- 2. Приклади розв'язування задач
- 3. Задачі для самостійної роботи
- Розділ ІІ. Перший закон термодинаміки
- 2.2. Приклади розв’язування задач
- 2.3. Задачі для самостійної роботи
- Розділ ІІІ. Пари, рідини та тверді тіла
- 3.2. Приклади розв’язування задач
- 3.3. Задачі для самостійної роботи
ВСТУП
Молекулярна фізика вивчає властивості речовини і явища, що зумовлені її мікроскопічною (молекулярною) будовою.
Через дуже велику кількість молекул у тілах (в 1 см3 твердої або рідкої речовини міститься біля 1023 молекул) їхні внутрішні властивості неможливо вивчати методами механіки. Тому в молекулярній фізиці використовуються власні специфічні методи – молекулярно-кінетичний і термодинамічний. Перший ґрунтується на аналізі властивостей і поведінки окремих молекул, а другий – на загальних закономірностях, що не залежать від подробиць внутрішньої будови речовини. Відповідно, молекулярна фізика традиційно поділяється на молекулярно-кінетичну теорію та термодинаміку. Проте слід зазначити, що такий поділ є доволі умовним, оскільки обидва методи є тісно взаємопов'язані й доповнюють один одного.
У молекулярній фізиці фізиці розглядаються різні агрегатні стани речовини (газоподібний, рідкий та твердий) і переходи між ними. Відповідно, посібник включає наступні розділи:
Розділ ІІ. Перший закон термодинаміки
Розділ ІІІ. Пари, рідини та тверді тіла
Кожен розділ містить:
1. Короткі теоретичні відомості
2. Приклади розв'язування задач
3. Задачі для самостійнї роботи
У самостійній роботі слід керуватися рекомендаціями з організації розв'язування задач та брати до уваги спрощення й наближення, що приймаються за промовчуванням.
Розділ І. Ідеальний газ
Молекулярно-кінетична теорія ґрунтується на наступних вихідних положеннях, які є узагальненням дослідних фактів:
– речовина складається з мікроскопічних частинок – атомів і молекул, які перебувають у безперервному хаотичному (тепловому) русі, інтенсивність якого визначає температуру тіла.
– молекули взаємодіють між собою: на порівняно великих відстанях притягаються, а на малих відштовхуються.
Залежно від величини сил зчеплення між молекулами речовина може перебувати в газоподібному, рідкому або твердому стані. Даний розділ присвячено ідеальним газам – речовинам, у яких сили притягання між молекулами практично відсутні.
Далі розглянуто
1. Теоретичні відомості
Розглянуто наступні питання:
1. Характеристики та тепловий рух молекул
1.1. Характеристики та тепловий рух молекул
Атоми і молекули мають дуже малі масу й розміри. До прикладу, маса одного з найважчих атомів — урану $^{238}U$ складає \( {4}\cdot {{10}^{-25}}\) кг, а розміри $\sim $ 10–10 м. Тому в атомній та молекулярній фізиці масу частинок вимірюють в умовних атомних одиницях маси, а для характеристики сукупної маси частинок у тілі вводять поняття кількості речовини та молярної маси.
Кількість речовини визначається кількістю структурних елементів (атомів або молекул), що входять до її складу, й вимірюється в умовних одиницях – молях:
1 моль – кількість речовини, що містить стільки ж молекул, як 12 г Карбону \( {}^{12}\mathrm{C} \).
Кількість частинок в одному молі, що називається числом Авогадро, є універсальною сталою і складає
|
N0 = 6,02·1023 1/моль. Тож кількість речовини, в якій міститься N молекул, у молях дорівнює
|
Відповідно, маса заданої кількості речовини
а кількість речовини в тілі із заданою масою
Масу однієї молекули m0 теж можна визначити через молярну масу, як
Температура. Молекули за будь-яких умов перебувають у стані неперервного теплового руху, інтенсивність якого визначає абсолютна температура Т – величина, що є прямо пов'язяна із середньою кінетичною енергією поступального руху молекули \( \left\langle E \right\rangle \) співвідношенням
коефіцієнт пропорційності k = 1,38·10–23 Дж/К в якому називається сталою Больцмана і є однією з універсальних фізичних констант. Зауваження. Формула (1.8) не є повною, позаяк не враховує енергію коливань атомів у складній молекулі та її обертання навколо власних осей. Але в елементарній молекулярній фізиці такі рухи не розглядають, і всі молекули за замовчуванням трактують як матеріальні точки. Одиницею температури є 1 кельвін (К) – величина, що складає (1/100) частку різниці температур кипіння та тверднення води за нормального атмосферного тиску. Величина T = 0 К називається абсолютним нулем температури і, як випливає із співвідношення (1.8), формально є температурою при якій припиняється тепловий рух атомів і молекул. Але, як свідчить теорія, елементарні частинки принципово не можуть перебувати в стані спокою. Тому абсолютний нуль температури є границею, до якої можна лише наблизитись. Через це на практиці для вимірювання температури використовують різні умовні температурні шкали. Для нас звичною є шкала Цельсія, в якій одиниця − градус Цельсія (1°С) – за розміром збігається з кельвіном, але за початок відліку 0°С прийнято температуру тверднення води, що дорівнює 273,15 ≈ 273 К. Тож на практиці співвідношення між значеннями температури в цих шкалах записують як
Нагадаємо також, що температуру T0 = 273,15 К (0°С) і тиск P0 = 101,3 кПа (760 мм.рт.ст.) називають нормальними умовами |
|
Температура характеризує не лишень енергію, а й швидкість теплового руху молекул. Якщо у формулі (1.8) виразити кінетичну енергію через швидкість, то вийде
де $\left\langle {{v}^{2}} \right\rangle$ є усередненою мірою інтенсивності теплового руху молекули. Відповідно, величина \( {{v}_{кв}}=\sqrt{\left\langle {{v}^{2}} \right\rangle }\) називається середньоквадратичною швидкістю, і визначається, як
де константа
називається універсальною газовою сталою. На завершення зауважимо, що тепловий рух молекул за мірками механіки є дуже інтенсивним. Так, згідно з виразами (1.9), середня квадратична швидкість молекул водню Н2 при кімнатній температурі складає близько 2000 м/с. |
1.2. Рівняння стану ідеального газу
|
Найбільш дослідженими в молекулярно-кінетичній теорії є гази. Зазвичай (при не екстремальних тисках й температурах) відстань між молекулами в газах є набагато більшою за їхні розміри, тож вони практично не взаємодіють між собою на відстані (див. п. 3.1). Тому за вказаних умов усяка газоподібна речовина виявляє однакові молекулярні властивості й розглядається в теорії як ідеальний газ — сукупність великої кількості частинок точкових розмірів, які не взаємодіють на відстані (не мають власної потенціальної енергії). В ідеальному газі молекули взаємодіють тільки при пружних зіткненнях між собою та з поверхнею тіл, з якими контактують. При цьому створюється тиск, який залежить від швидкості молекул та частоти зіткнень і, як доведено в теорії, дорівнює
де n — концентрація молекул (кількість в одиниці об'єму), і $\left\langle E \right\rangle $ — середня кінетична енергія теплового руху молекули. Тож, якщо врахувати вираз (1.8), вийде
або
Із співвідношення (1.11a) випливає закон Авогадро:
Зокрема, в усіх газах концентрація молекул за нормальних умов складає n0 = 2,69·1025 1/м3. Розділивши на це число сталу Авогадро, отримаємо об'єм одного моля або молярний об'єм ідеального газу за нормальних умов: V0 = 22,4·10–3 м3/моль. Концентрація молекул у суміші газів, що хімічно не взаємодіють між собою, дорівнює сумі концентрацій компонент: $n={{n}_{1}}+{{n}_{2}}+...=\sum{{{n}_{i}}}$. Тож із рівняння (1.11) отримуємо закон Дальтона для газових сумішей, а саме, тиск суміші газів дорівнює сумі парціальних тисків компонент (тисків окремих компонент за відсутності решти):
|
Величини, які можна вимірювати (тиск , об'єм і температура), називаються параметрами стану газу, а безпосередній зв'язок між ними — рівнянням стану. Рівняння стану ідеального газу, або рівняння Клапейрона, можна отримати з виразів (1.11) та (1.11а). Якщо за допомогою співвідношень (1.3) і (1.6) виключити з них величини N і n, то вийде:
де ν – кількість (в молях), m і M– маса та молярна маса газу, R = kN0 – універсальна газова стала. Наостанку ще раз зазначимо, що модель ідеального газу добре відтворює властивості більшості реальних газів в широкому діапазоні температур і тисків, окрім надвисоких і наднизьких.
|
1.3. Ізопроцеси (газові закони)
Рівняння Клапейрона пов'язує параметри ідеального газу в стані термодинамічної рівноваги, коли його температура, тиск та об'єм не змінюються з часом. Але рівняння (1.13) і (1.14) зберігють чинність і при зміні параметрів у так званих рівноважних процесах, в яких вирівнювання параметрів по всьому об'єму відбувається набагато швидше, ніж їхня помітна зміна в якомусь місці. В такому випадку при незмінній кількості ν параметри стану в два довільні моменти часу є пов'язані об'єднаним газовим законом:
|
$\frac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}}$. |
(1.15) |
|
Ізотермічний процес. При T = const із рівняння (1.14) виходить
Отже, при незмінній температурі добуток тиску та об'єму заданої кількості ідеального газу лишається сталим:
У цьому полягає закон Бойля-Маріотта, з якого випливає, що при однаковій температурі для будь-яких двох станів
|
|
При ізобарному процесі (P = const) рівняння (1.13) набуває вигляду:
і виражає закон Гей-Люссака:
Із рівняння (1.16) випливає, що при однаковому тиску для будь-яких двох станів
де V0 – об'єм газу при температурі \(0\ {}^\circ \text{C}\), і \(\alpha \) – коефіцієнт термічного розширення газу, що визначається виразом:
|
|
В ізохорному процесі (V = const) з рівняння (1.13) маємо:
яке виражає закон Шарля:
Із рівняння (1.19) випливає, що при однаковому об'ємі для будь-яких двох станів газу
У шкалі Цельсія рівняння закону Шарля має вигляд
де P0 - тиск при температурі 0°С, \(\beta \) – термічний коефіцієнт тиску газу, котрий визначається як
Термічні коефіцієнти об'єму α та тиску β показують, на яку частку змінюється відповідний параметр газу при зміні температури на одиницю за умови, що інший параметр лишається незмінним. Для ідеального газу вказані термічні коефіцієнти збігаються і становлять: \(\alpha =\beta =\frac{1}{273}\) $\left( \frac{1}{\operatorname{K}} \right)$.
|
2. Приклади розв'язування задач
У всіх прикладах газ по умовчанню вважається ідеальним, і для енергії молекули приймаються формули (1.8) та (1.8а).
Відповідно до п. 1.1 задачі згруповано по наступних темах:
Характеристики молекул
Задача 1.1. У досліді з визначення розмірів молекули на поверхню води в широкій посудині помістили краплину незмішуваного з нею спиртового розчину олеїнової кислоти й після її розтікання та випаровування спирту виміряли розміри плями, що утворилася. Оцінити поперечник d молекули, якщо при об'ємі краплі V0 = 2 мм3 і концентрації розчину С = 0,5 % діаметр плями склав D = 20 см.
Задача 1.2. А) Отримати формулу для оцінки діаметра d молекули заданої речовини за її густиною. Б) Оцінити діаметри атомів літію Li (ρ1 = 0,53·103 кг/м3), ртуті Hg (ρ2 = 13,6·103 кг/м3), урану U (ρ3 = 19,05·103 кг/м3) і молекули води H2O (ρ4 = 1,0·103 кг/м3).
Задача 1.3. Визначити масу m0 молекули газу, який за нормальних умов (T0 = 273 K, P0 = 105 Па) має густину ρ = 1,94 кг/м3.
Задача 1.4. Визначити відношення кількостей атомів (N1/N2) в однакових посудинах, одну з яких заповнено водою, а іншу ртуттю.
Задача 1.5. Концентація молекул повітря при нормальному атмосферному тиску й кімнатній температурі дорівнює n = 2,5·1019 см–3. Визначити, протягом якого часу за таких умов можна було би повністю відкачати посудину об'ємом V = 1 л насосом, який був би спроможний постійно викидати назовні один мільярд молекул за секунду.
Задача 1.6. Визначити молярну масу повітря М, вважаючи, що воно за масою складається з с1 = 75,5 % азоту N2, с2 = 23,1 % кисню O2, с3 = 1,3 % аргону Ar і с4 = 0,1 % вуглекислого газу CO2.
Задача 1.7. Визначити середню квадратичну швидкість: А) компонент повітря – молекули водню (H2) та атома аргону (Ar) і Б) мікроскопічної порошинки піску (SiO2) розміром d = 0,1 мкм, яка є зважена ("плаває") у повітрі. Густина піску ρ = 2,5 г/см3, температура повітря t = 20 °С
Задача 1.8. Температуру в кімнаті площею S = 20 м2 і висотою стелі h = 3 м підвищують від t1 = 15 °C до t2 = 25 °C при атмосферному тиску P = 100 кПа. Визначити, на скільки при цьому змінюється: А) кількість молекул повітря в кімнаті ΔN; Б) сумарна кінетична енергія їхнього теплового руху \( \Delta{U}\).
Задача 1.9. Три балони ємністю V1 = 2 л, V2 = 3 л і V3 = 5 л, які сполучено тонкими трубками з перекритими кранами, містять гази під тиском P1 = 100 кПа, P2 = 80 кПа і P3 = 40 кПа. Визначити тиск P, який установиться в системі після відкриття кранів.
Задача 1.10. В одну половину відкачаного циліндра, що розділений жорсткою напівпроникною перегородкою (мембраною), швидко впускають суміш газів, яка складається з однакових кількостей водню (М1 = 2 г/моль) та гелію (М2 = 4 г/моль) і має тиск P0 = 100 кПа. Визначити тиски P1 і P2 в обох половинах циліндра після припинення дифузії, якщо мембрана пропускає тільки водень, і температура в процесі лишається сталою.
Задача 1.11. Два однакові балони з термостійкого матеріалу сполучено тонкою трубкою й заповнено газом під тиском P0. Визначити максимальний тиск Pm, який теоретично можна одержати в системі, нагріваючи один балон і підтримуючи інший при сталій температурі.
Задача 1.12. В одну частину розділеного рухомою непроникною перегородкою циліндра вміщено m1 = 2 г водню H2, а в іншу m2 = 32 г кисню O2 при температурі \(t\gt{100}^{\circ}\mathrm{C}\). Тиск у системі P0 = 100 кПа. Визначити тиск P в циліндрі після того, як прибрали перегородку і встановилася початкова температура.
Задача 1.13. Визначити тиск P, що його чинить на стінку пучок молекул водню Н2 з концентрацією n = 3·1023 1/м3 при при перпендикулярному падінні й пружному відбиванні від неї зі швидкістю $v$ = 1 км/с .
SOLUTION
У досліді з визначення розмірів молекули на поверхню води в широкій посудині помістили краплину незмішуваного з нею спиртового розчину олеїнової кислоти й після її розтікання та випаровування спирту виміряли розміри плями, що утворилася.
Оцінити
поперечник d молекули, якщо крапля її спиртового розчину концентрацією С = 0,5 % й об'ємом V0 = 2 мм3 розпливлася в круглу пляму діаметром D = 20 см.
|
Дано: С = 0,5 %
V0 = 2 мм3
D = 20 см
|
|
d - ?
|
Розв’язання
Ідея описаного досліду ґрунтується на тому, що крапля розтікається по поверхні води аж до утворення плівки (плями) завтовшки в одну молекулу. Тож розміри молекули можна оцінити за товщиною h такої мономолекулярної плівки.
Зрозуміло, що прямо виміряти величину h неможливо, але її можна визначити опосередковано, вважаючи, що через швидке випаровування летючого розчинника (спирту) молекули кислоти розташовуються впритул, утворюючи на воді суцільний шар в одну молекулу. В такому разі поперечник молекули дорівнює його товщині h:
|
|
\(d\approx h=\frac{V}{S}\) \( \Rightarrow \) \( d\approx \frac{4V}{\pi {{D}^{2}}},\) |
(1) |
де V – об'єм , \(S=\pi {{D}^{2}}/4\) – площа поверхні утвореної плівки.
Концентрація розчину дорівнює відношенню об'єму V кислоти в краплі до об'єму V0 розчину: с = V/V0. Отже, об'єм плівки на воді V = cV0. Підставивши цю величину у формулу (1), одержимо:
|
\(d\approx \frac{4c{{V}_{0}}}{\pi {{D}^{2}}},\) = 3·10–10 м = 0,3 нм. |
(2) |
Щодо отриманого результату слід зауважити таке. Формула (2) є оціночною, а не точною. Адже коли уявити молекули мікроскопічними кульками, то навіть при щільному розташуванні між ними існуватимуть пустоти, що у виразах (1) і (2) не враховано. Але насправді ситуація є ще складніша, бо молекули є не мікроскопічними кульками, а складною системою електронів, які рухаються навколо ядер за законами квантової механіки. Тож саме поняття розміру для атомів і молекул не має такого визначеного змісту, як для макроскопічних частинок.
А) Отримати
формулу для оцінки діаметра d молекули заданої речовини за її густиною.
Б) Оцінити
діаметри: атомів літію Li (ρ1 = 0,53·103 кг/м3), ртуті Hg (ρ2 = 13,6·103 кг/м3), урану U (ρ3 = 19,0·103 кг/м3) і молекули води H2O (ρ4 = 103 кг/м3).
|
Дано: ρ1 = 0,53·103 кг/м3
ρ2 = 13,6·103 кг/м3
ρ3 = 19,0·103 кг/м3
ρ4 = 1·103 кг/м3
--- ----
|
|
d1, d2, d3, d4 - ?
|
Розв’язання
А) 1 моль речовини містить N0 = 6,02·1023 молекул (стала Авогадро) і займає об'єм
\({{V}_{m}}=\frac{M}{\rho },\)
де M – молярна маса, \(\rho \) – густина. У рідинах і твердих тілах молекули розміщені впритул, тому об'єм і розміри однієї молекули можна оцінити, відповідно, як
\({{V}_{0}}\approx \frac{{{V}_{m}}}{{{N}_{0}}}=\frac{M}{\rho {{N}_{0}}},\)
і
|
|
\(d\approx \sqrt[3]{{{V}_{0}}}=\sqrt[3]{\frac{M}{\rho {{N}_{0}}}}.\) |
(1) |
Б) Узявши відносні атомні маси з таблиці хімічних елементів, із співвідношення (1.4) одержимо наступні значення молярної маси: літій M1 = 6,94·10–3 кг/моль, ртуть M2 = 200,6·10–3 кг/моль, уран M3 = 238·10–3 кг/моль і вода M4 = 18·10–3 кг/моль. Відтак за формулою (1) оцінимо діаметри атомів заданих елементів та молекули води: літій Li \({{d}_{1}}\approx 2,8\cdot {{10}^{-10}}\text{м};\) ртуть Hg \({{d}_{2}}\approx 2,9\cdot {{10}^{-10}}\ \text{м};\) уран U \({{d}_{3}}\approx 2,75\cdot {{10}^{-10}}\ \text{м}\); вода H2O \({{d}_{4}}\approx 3,1\cdot {{10}^{-10}}\ \text{м}.\)
В результатах упадає в око близькість отриманих чисел при великій різниці густин, отож мас атомів і кількості нуклонів у ядрах. Це пов'язано з особливостями взаємодії елементарних частинок, які не дозволяють уважати їх просто мікроскопічними твердими кульками.
Задача 1.3
Визначити
масу m0 молекули газу, який за нормальних умов (T0 = 273 K, P0 = 105 Па) має густину \( {{\rho }_{0}}=1,94 \) кг/м3.
|
Дано: T0 = 273 K P0 = 105 Па
ρ =1,94 кг/м3
|
|
m0 - ? |
Розв’язання
Густина чисельно дорівнює масі одиниці об'єму речовини. Тож
\( \rho ={{m}_{0}}n, \)
де m0 – маса однієї молекули, n – концентрація (кількість в одиниці об'єму) молекул у речовині. Таким чином,
|
\( {{m}_{0}}=\frac{{{\rho }_{0}}}{{{n}_{0}}}, \) |
|
де \( {{\rho }_{0}}\), n0 – густина й концентрація газу за нормальних умов.
Згідно з формулою (1.11),
\( {{n}_{_{0}}}=\frac{{{P}_{0}}}{k{{T}_{0}}}, \)
отже,
\( {{m}_{0}}=\frac{\rho k{{T}_{0}}}{{{P}_{0}} }= 7,3\cdot {{10}^{-26}}\ \text{кг}. \)
Визначити
Визначити відношення кількостей атомів (N1/N2) в однакових посудинах, одну з яких заповнено водою, а іншу ртуттю.
|
Дано: H2O, Hg
--2
|
|
N1/N2 - ?
|
Розв’язання
Молекула води складається з трьох атомів. Тож відповідно до формул (1.3) и (1.6) кількість атомів у посудині з водою
|
|
${{N}_{1}}=3\frac{{{m}_{1}}}{{{M}_{1}}}{{N}_{0}}$, |
|
де m1 – маса і M1 – молярна маса води, N0 – стала Авогадро. Відтак, виразивши масу m1 через густину води ρ1 і об'єм посудини V, дістанемо:
\({{N}_{1}}=\frac{3{{\rho }_{1}}V{{N}_{0}}}{{{M}_{1}}}.\)
Аналогічно визначається кількість атомів ртуті у другій склянці:
\({{N}_{2}}=\frac{{{\rho }_{2}}V{{N}_{0}}}{{{M}_{2}}}\).
Отже, шукане відношення
|
|
\(\frac{{{N}_{1}}}{{{N}_{2}}}=\frac{3{{\rho }_{1}}}{{{\rho }_{2}}}\cdot \frac{{{M}_{2}}}{{{M}_{1}}}.\) |
|
Узявши з таблиць значення \( \rho_{1}=10^{3}\) кг/м3, \( \rho_{2}=13,6 \cdot{10}^{3}\) кг/м3, \({{M}_{1}}=18\cdot{{10}^{-3}}\) кг/моль, і \({{M}_{2}}=201\cdot {{10}^{-3}}\)кг}/моль, одержимо:
$\frac{{{N}_{1}}}{{{N}_{2}}}\approx 2,5$.
Таким чином, атомів у склянці з водою є істотно більше, ніж у склянці зі ртуттю. А от кількості молекул води Nв й атомів ртуті Nрт є приблизно однакові:
\(\frac{{{N}_{в}}}{{{N}_{рт}}}=\frac{{{\rho }_{2}}}{{{\rho }_{1}}}\cdot \frac{{{M}_{1}}}{{{M}_{2}}}\approx 1,2.\)
Це пояснюється тим, що молекула води й атом ртуті мають близькі розміри (див. задачу (1.2)), тому їхні кількості в однаковому об'ємі теж мало відрізняються.
Концентація молекул повітря при нормальному атмосферному тиску й кімнатній температурі дорівнює n = 2,5·1019 см–3 .
Визначити,
протягом якого часу за таких умов можна було би повністю відкачати посудину об'ємом V = 1 л насосом, який був би спроможний постійно викидати назовні один мільярд молекул за секунду.
|
Дано: V = 1 л
n = 3,2·1025 м-3
n1 = 109 c-1 |
|
t - ?
|
Розв'язання
Час відкачування t = (N/n1), де n1 – кількість молекул, що захоплюються насосом за 1 c, N – їхня початкова кількість у посудині. Позаяк N = nV, то
\(t=\frac{nV}{{{n}_{1}}}\) ≈ 800 тис. років.
Можна вважати, що повітря складається за масою з \( {c}_{1}\) = 75,5 % азоту N2, \( {c}_{2}\) = 23,1 % кисню O2, \( {c}_{3}\) = 1,3 % аргону Ar і \( {c}_{4}\) = 0,1 % вуглекислого газу CO2.
Визначити
молярну масу повітря М.
|
Дано: \( {c}_{1}\) = 75,5 %
\( {c}_{2}\) = 23,1 %
\( {c}_{3}\) = 1,3 %
\( {c}_{4}\) = 0,1 %
|
|
M - ?
|
Розв’язання
Молярна маса, котра є мірою кількості речовини, визначається кількістю частинок, яка міститься в тілі, а не його масою чи якоюсь іншою величиною. Отже, в одному молі повітря міститься \({{N}_{0}}=6,02\cdot {{10}^{23}}\) молекул газів-компонент у відповідних пропорціях.
Нехай маса повітря дорівнює m. Тоді загальна кількість молекул у посудині
|
|
\( {N}=\frac{m}{M}{{N}_{0}},\) |
(1) |
де M – його молярна маса, N0 – стала Авогадро. Очевидно, що
|
|
\(N=N_{1}+N_{2}+N_{3}+N_{4}=\frac{m_{1}}{M_{1}}N_{0}+\frac{m_{2}}{M_{2}}N_{0}+\frac{m_{3}}{M_{3}}N_{0}+\frac{m_{4}}{M_{4}}N_{0}\). |
(2) |
Тут, відповідно, \( {{N}_{1}},\ {{N}_{2}},\ {{N}_{3}},\ {{N}_{4}}\) – кількість молекул, \( {{m}_{1}},\ {{m}_{2}},\ {{m}_{3}},\ {{m}_{4}}\) – маси, а \( {{M}_{1}},\ {{M}_{2}},\ {{M}_{3}},\ {{M}_{4}}\) – молярні маси компонент. При масі суміші m маса і-ї компоненти mі визначається її концентрацією і складає mі = сіm. Тож
\( {{m}_{1}}={{c}_{1}}m,\ \ {{m}_{2}}={{c}_{2}}m,\ \ {{m}_{3}}={{c}_{3}}m,\ \ {{m}_{4}}={{c}_{4}}m. \)
Таким чином, з (2) маємо:
|
|
\( {N}=m\left(\frac{c_{1}}{M_{1}}+\frac{c_{2}}{M_{2}}+\frac{c_{3}}{M_{3}}+\frac{c_{4}}{M_{4}} \right){{N}_{0}}\\ \). |
(3) |
Прирівнявши праві частини виразів (1) і (3), знаходимо вирази
|
|
\( \frac{1}{M}=\frac{c_{1}}{M_{1}}+\frac{c_{2}}{M_{2}}+\frac{c_{3}}{M_{3}}+\frac{c_{4}}{M_{4}}\), |
|
або
|
|
\( {M}={{\left( \frac{{{c}_{1}}}{{{M}_{1}}}+\frac{{{c}_{2}}}{{{M}_{2}}}+\frac{{{c}_{3}}}{{{M}_{3}}}+\frac{{{c}_{4}}}{{{M}_{4}}} \right)}^{-1}}.\) |
|
Узявши з таблиць молярні маси M1 = 28 г/моль, M2 = 32 г/моль, M3 = 40 г/моль, M4 = 44 г/моль, після обчислень отримаємо:
M= 29 г/моль .
Слід сказати, що насправді повітря, крім зазначених, містить деяку кількість інших газів, таких як водень, гелій та ін. Тому в умові величину c4 свідомо дещо змінено так, аби отриманий результат збігався з табличним значенням молярної маси повітря. Зазначимо також, що в наведених викладках кількість компонент у суміші та їхній агрегатний стан були не істотними. Тож отриманий результат можна узагальнити й записати наступну загальну формулу молярної маси суміші будь-якої кількості заданих речовин із відомим відсотковим умістом:
\( \frac{1}{M}=\sum\frac{c_{i}}{M_{i}}\), \(M=\left( \sum\frac{c_{i}}{M_{i}} \right)^{-1}\).
Визначити
середньоквадратичну швидкість:
А) компонент повітря – молекули водню (H2) та атома аргону (Ar) і
Б) мікроскопічної порошинки піску (SiO2) розміром d = 0,1 мкм, яка є зважена ("плаває") у повітрі. Густина піску ρ = 2,5 г/см3, температура повітря t = 20 °С
|
Дано: H2, Ar , SiO2
d = 0,1 мкм
ρ = 2,5 г/см3
t = 20 °С
|
|
v1, v2, v3 - ?
|
Розв’язання
А) Середня квадратична швидкість молекул газу при заданій температурі визначається формулами (1.9). Визначивши за таблицею хімічних елементів молярні маси молекулярного водню (H2) M1 = 2·10–3 кг/моль і аргону (Ar) M2 = 40·10–3 кг/моль і врахувавши температура повітря T = 293 K і газову сталу R= 8,31 Дж/(моль·К), знаходимо:
\( {{v}_{1}}=\sqrt{\frac{3RT}{{{M}_{1}}}}\) ≈ 1900 м/с,
\( {{v}_{2}}=\sqrt{\frac{3RT}{{{M}_{2}}}}\) ≈ 430 м/с.
Б) Порошинці не дають падати молекули повітря, що "бомбардують" її з усіх боків і змушують здійснювати хаотичний броунівський рух. З цієї ж причині не падають на землю і самі молекули повітря. Так що рух порошинки має ту саму природу і властивості, що й тепловий рух молекул. Зокрема, кінетична енергія поступального (броунівського) руху порошинки визначається формулою (1.8), а середньоквадратична швидкість \( {{v}_{3}}\) –формулою (1.9):
|
|
\( {{v}_{3}}=\sqrt{\frac{3kT}{m}},\) |
(1) |
Маса порошинки \( {m=\rho V}\), де \( \rho \) – густина її речовини, V – об'єм. Форма порошинки точно не відома, тому її об'єм і масу можна тільки розумно оцінити, приміром, прийнявши за кубик з ребром d. Тоді
\( {m}=\rho {{d}^{3}},\)
і відповідно до формули (1)
v3 \(\sim \sqrt{\frac{3kT}{\rho {{d}^{3}}}}\).
Підставивши сюди задані значення \( {T},\ d,\ \rho \), а також k = 1,38·10–23 Дж/К, одержимо
v3 \(\sim \) 7 м/с.
Упадає в око те, що швидкість порошинки є дуже малою порівняно зі швидкостями молекул: \( ({{v}_{1}}/{{v}_{3}})\approx 3\cdot {{10}^{4}}\), \( ({{v}_{2}}/{{v}_{3}})\approx 6\cdot {{10}^{3}}\). Але нічого дивного в цьому немає, бо порошинка, попри те що є видима тільки під мікроскопом, складається з \( {N}\cong 2,5\cdot {{10}^{7}}\) молекул. Тож її маса (інертність) є несумірно великою порівняно з масою молекули. Тому, обмінюючись при зіткненнях з молекулами повітря однаковими енергією та імпульсом, вона здобуває набагато меншу швидкість.
Температуру в кімнаті площею \( {S}=20\ м^{2}\) і висотою стелі h = 3 м підвищують від t1 = 15 °C до t2 = 25 °C при атмосферному тиску P = 100 кПа.
Визначити,
на скільки при цьому змінюється:
А) кількість молекул повітря в кімнаті ΔN;
Б) сумарна кінетична енергія їхнього теплового руху U.
|
Дано: S = 20 м2
h = 3 м
t1 = 15 °C
t2 = 25 °C
P = 100 кПа
|
|
\( \Delta N \) - ?
\( \Delta{U}\) - ?
|
Розв’язання
А) Зміна кількості молекул повітря в кімнаті
|
\( \Delta N={{N}_{2}}-{{N}_{1}}=({{n}_{2}}-{{n}_{1}})Sh, \) |
(1) |
де n1, n2 – концентрації молекул при температурі t1 і t2 відповідно, Sh = V– об'єм повітря в кімнаті. Кімната не є "герметичною посудиною", тому при зміні температури тиск повітря в ній залишається сталим і дорівнює атмосферному. Тож, з формули (1.11) маємо:
\( {{n}_{2}}=\frac{P}{k{{T}_{2}}},\ \ \ \ \ \ \ \ {{n}_{1}}=\frac{P}{k{{T}_{1}}}.\)
Після підстановки цих значень у вираз (1) одержуємо відповідь:
\( \Delta N=\frac{PSh}{k}\left( \frac{1}{{{T}_{2}}}-\frac{1}{{{T}_{1}}} \right)\) ≈ –5·1025.
Знак "–" означає, що при нагріванні повітря молекули виходять з кімнати.
Б) Зміна сумарної кінетичної енергії теплового руху молекул повітря в кімнаті
|
\( \Delta U={{U}_{2}}-{{U}_{1}}={{N}_{2}}\left\langle {{E}_{2}} \right\rangle -{{N}_{1}}\left\langle {{E}_{1}} \right\rangle =V\left( n{}_{2}\left\langle {{E}_{2}} \right\rangle -{{n}_{1}}\left\langle {{E}_{1}} \right\rangle \right), \) |
(2) |
де V – об'єм повітря, n1 і n2 – концентрації молекул, а \( \left\langle {{E}_{1}} \right\rangle \) і \( \left\langle {{E}_{2}} \right\rangle \) – середні кінетичні енергії молекули при початковій і при кінцевої температурах. Відповідно до основного рівняння молекулярно-кінетичної теорії ідеального газу (1.10) можна записати \( {n}\left\langle E \right\rangle =3P/2 \). Підставивши цей вираз в рівняння (2) і врахувавши незмінність тиску, дістанемо
\( \Delta U=0. \)
Таким чином, при зміні температури в кімнаті енергія теплового руху молекул повітря не змінюється. Цей, можливо неочікуваний, результат легко пояснюється: при підвищенні температури повітря кінетична енергія однієї молекули збільшується рівно у стільки разів, у скільки зменшується їхня кількість у кімнаті.
Три балони ємністю V1 = 2 л, V2 = 3 л і V3 = 5 л, які сполучено тонкими трубками з перекритими кранами, містять гази під тиском P1 = 100 кПа, P2 = 80 кПа і P3 = 40 кПа.
Визначити
тиск P, який установиться в системі після відкриття кранів.
|
Дано: V1 = 2 V2 = 3л V3 = 5 л P1 = 100 кПа P2 = 80 кПа P3 = 40 кПа |
|
P - ?
|
Розв’язання
Після відкривання кранів утворюється суміш газів у посудині об'ємом
|
$V=\sum{{{V}_{i}}}$, |
|
тиск якої за законом Дальтона (1.12)
|
$P=\sum{{{P}_{i}}^{\prime }}$. |
|
У цьому виразі парціальні тиски компонент суміші ${{{P}'}_{i}}$ (див. п. 1.1), за рівнянням (1.11) визначаються температурою та їхніми концентраціями \( {{n}_{i}}^{\prime }\) в об'єднаному балоні, як
|
$P=\sum{{{n}_{i}}^{\prime }}kT$, |
|
де
|
\( {{n}_{i}}^{\prime } \) = $\frac{{{N}_{i}}}{V}$ = $\frac{{{n}_{i}}{{V}_{i}}}{\sum{{{V}_{i}}}}$. |
Отже, тиск у об'єднаному балоні
$P=\frac{\sum{{{n}_{i}}kT{{V}_{i}}}}{\sum{{{V}_{i}}}}$,
і, згідно з рівнянням (1.11),
|
|
$P=\frac{\sum{{{P}_{i}}{{V}_{i}}}}{\sum{{{V}_{i}}}}$. |
|
Для заданої в умові кількості сполучених балонів розгорнута відповідь має вигляд:
\(P=\frac{{{P}_{1}}{{V}_{1}}+{{P}_{2}}{{V}_{2}}+{{P}_{3}}{{V}_{3}}}{{{V}_{1}}+{{V}_{2}}+{{V}_{3}}}\) = 64 кПа.
В одну половину відкачаного циліндра, що розділений жорсткою напівпроникною перегородкою (мембраною), швидко впускають суміш газів, яка складається з однакових кількостей водню (М1 = 2 г/моль) та гелію (М2 = 4 г/моль) і має тиск P0 = 100 кПа.
Визначити
тиски P1 і P2 в обох половинах циліндра після припинення дифузії, якщо мембрана пропускає тільки водень, і температура в процесі лишається сталою.
|
Дано: P0 = 100 кПа
ν1 = ν2
|
|
P1 - ? P2 - ?
|
Розв’язання
Рис. 10 схематично ілюструє початковий (а) і кінцевий (б) стан системи.
Позаяк кількості газів однакові, то початкові концентрації молекул n0 у них теж однакова. Отже, згідно з рівнянням (1.11) і законом Дальтона (1.12), початковий тиск
|
${{P}_{0}}=2{{n}_{0}}kT\quad \Rightarrow \quad {{n}_{0}}=\frac{{{P}_{0}}}{2kT}$. |
Після припинення дифузії водню крізь мембрану в лівій половині циліндра залишається суміш із усього гелію із парціальним тиском
PHe = $\frac{{{P}_{0}}}{2}$
та половини водню з концентрацією (n0/2) і парціальним тиском
PH = $\frac{{{P}_{0}}}{4}$.
Отже, повний тиск у лівій половині циліндра
P1 = PHe + PH = $\frac{3}{4}{{P}_{0}}$ = 75 кПа.
У правій половині
P2 = PH = $\frac{{{P}_{0}}}{4}$ = 25 кПа.
Два однакові балони з термостійкого матеріалу сполучено тонкою трубкою й заповнено газом під тиском P0.
Визначити
максимальний тиск Pm, який теоретично можна одержати в системі, нагріваючи один балон і підтримуючи інший при сталій температурі.
|
Дано: V1 = V2
\( {P}_{0}\)
|
|
\( {P}_{m}\) - ?
|
Розв’язання
Нехай температура в першому балоні підтримується на заданому рівні T0, а в другому має якесь значення T > T0. Тоді, позаяк тиски в сполучених балонах є однакові за будь-яких умов, із рівняння (1.11) маємо:
|
\( {{n}_{1}}k{{T}_{0}}={{n}_{2}}kT \) \( \Rightarrow \) \( \frac{{{n}_{2}}}{{{n}_{1}}}=\frac{{{T}_{0}}}{T}. \) |
(1) |
Отже, при підвищенні температури Т другого балона концентрація молекул у ньому буде зменшуватись, а в першому – відповідно збільшуватись, тобто газ перетікатиме з гарячого балона в холодний. Це пояснюється тим, що кількість молекул, які проходять по трубці за 1 с в той чи інший бік, є прямо пропорційна швидкості їхнього руху, котра зростає при нагріванні.
За умовою другий балон теоретично можна нагріти до гранично високої температури, тож із співвідношення (1) при Т → ∞ маємо n2 → 0. Це означає, що всі молекули з гарячого балона перейдуть у холодний і концентрація молекул та тиск у ньому подвояться.
Таким чином, теоретично можливий максимальний тиск у системі складає
Pmax = 2P0.
В одну частину розділеного рухомою непроникною перегородкою циліндра вміщено m1 = 2 г водню H2, а в іншу m2 = 32 г кисню O2 при температурі \(t\gt{100}^{\circ}\mathrm{C}\). Тиск у системі P0 = 100 кПа.
Визначити
тиск P в циліндрі після того, як прибрали перегородку і встановилася початкова температура.
|
Дано: H2, O2 m1 = 2 г m2 = 32 г
\(t\gt{100}^{\circ}\mathrm{C}\)
|
|
P - ?
|
Розв’язання
З умови видно, що спочатку в циліндрі було по 1 моль кожного газу, тобто однакова кількість молекул
N1 = N2 = N0,
де N0 = 6,02·1023. Початкові об'єми газів теж однакові й дорівнюють половині об'єму циліндра:
V1 = V2 = V/2.
Після прибирання перегородки відбувається реакція окислення водню при температурі \(t\gt{100}^{\circ}\mathrm{C}\):
|
2H2 + O2 = 2H2O, |
(1) |
результатом якої є утворення водяної пари. При цьому на утворення двох молекул води йде дві молекули водню, але тільки одна молекула кисню. Тому весь водень прореагує з половина кисню, і в циліндрі утвориться суміш водяної пари з киснем загальною кількістю молекул
\( {N}=\frac{3}{2}{{N}_{0}}. \)
Позначимо об'єм циліндра і кінцеву температуру суміші як V і T. Тоді кінцевий тиск за формулою (1.11) складає:
|
|
\(P=\frac{3{{N}_{0}}k{{T}}}{2V},\) |
(2) |
За умовою задачі початкові температури й тиски газів, тож і концентрації молекул, є однакові:
\( {{n}_{1}}={{n}_{2}}\) \( \Rightarrow \) \( \frac{{{N}_{1}}}{{{V}_{1}}}=\frac{{{N}_{2}}}{{{V}_{2}}}. \)
Вище було встановлено, що N1 = N2 = N0, тому на підставі формули (1.11) можна записати
|
|
\( {{P}_{0}}=\frac{{{N}_{0}}}{(V/2)}k{{T}}\) \( \Rightarrow \) \( {{P}_{0}}=\frac{2{{N}_{0}}k{{T}}}{V}. \) |
(3) |
Порівнявши вирази (2) і (3), одержимо відповідь:
\( {P}=\frac{3}{4}{{P}_{0}}. \)
Задача 1.13.
Визначити
тиск P, що його чинить на стінку пучок молекул водню з концентрацією n = 1023 1/м3 при перпендикулярному падінні й пружному відбиванні від неї зі швидкістю $v$ = 1 км/с .
|
Дано: n = 1023 1/м3 $v$ = 1 км/с |
|
P-? |
Розв'язання
При пружньому перпендикулярному зіткненні зі стінкою кожна молекула, що підлітає зі швидкістю $\vec{v}$ відскакує в зворотньому напрямку з такою самою за модулем швидкістю –${\vec{v}}'$, змінюючи свій імпульс на величину $\Delta \vec{p}=m{\vec{v}}'-m\vec{v}=-2m\vec{v}$. Тож, позаяк за законами механіки сила, що діє на тіло, чисельно дорівнює зміні його імпульсу за одиницю часу, сила тиску F та тиск пучка молекул на стінку складають:
| $F=2mvZ$, $P=\frac{2mvZ}{S}$, | (1) |
де S – площа поперечного перерізу пучка і Z – кількість зіткнень молекул зі стінкою за одиницю часу.
Величину Z легко підрахувати, позаяк за час t зі стінкою стикаються всі молекули, що перебувають від неї на відстанях $l\le vt$. Тож $Z=nvS$, і
$P=2nm{{v}^{2}}$.
Відтак, підставивши вираз маси молекули (1.7) і врахувавши табличні константи, отримаємо відповідь:
$P=\frac{2nM{{v}^{2}}}{{{N}_{\text{A}}}}$ = 2 кПа.
Рівняння стану ідеального газу
У задачах із молекулярної фізики є широко вживаними позасистемні одиниці такі, як (а.о.м.), (мм.рт.ст.) та (°С). Тому варто ще до початку розв'язування перевести числові дані в основні одиниці CІ, як це зроблено далі.
Задача 1.14. У балоні об'ємом V = 1 л міститься m = 1,0 г невідомого окислу азоту NxOy при температурі t = 27°C і тиску P = 32,8 кПа. Встановити хімічну формулу сполуки (визначити x та y). Газова стала R = 8,31 Дж/(моль·К).
Задача 1.15. Балон із киснем при тиску P1 = 1 МПа і температурі t1 = 27 °C винесли надвір і підключили до газового пальника. Визначити, який відсоток η (%) кисню було витрачено, коли на кінець роботи тиск у балоні впав до P2 = 600 кПа при температурі t2 = –23 °C.
Задача 1.16. Відкачану посудину об'ємом V = 0,5 л, що містила m = 1 г кристалічного йоду I2, нагріли до t = 1000°C, через що він випарувався і частково дисоціював на атоми. Визначити частку молекул I2 , що дисоціювали, якщо в посудині встановився тиск P = 700 мм.рт.ст. Атомна маса йоду Ar = 127.
Задача 1.17. Відкачаний балон, який на \( \eta=0,1 \) об'єму заповнено водою, вміщають у термостат із температурою t = 300°C. Визначити, чи розірветься балон, якщо він витримує максимальний тиск P0 = 25 МПа.
Задача 1.18. У балоні об'ємом V = 10 л міститься газова суміш гелію і неону загальною масою m = 36 г при тиску \(P=10^{6}\) Па і температура t = 28°C. Визначити масу гелію m1 і неону m2 в суміші.
Задача 1.19.При електролізі (розкладанні молекул електричним струмом) із m = 1 кг води отримано V = 710 л кисню під тиском P = 105 Па. Визначити температуру газу t°С.
Задача 1.20. У кожній частині закритого вертикального циліндра із рухомим масивним поршнем заходиться по ν = 1 моль повітря. Визначити, за якої температури T2 відношення об'ємів повітря дорівнюватиме η2 = 3, якщо при температури T1 = 320 K воно складає η1 = 4.
Задача 1.21. Два однакові балони, один із газом при тиску P1 = 1,0 атм і температурі t1= 27°C, а інший порожній, є сполучені трубкою з клапаном, який починає пропускати при різниці тисків у балонах ΔР ≥ 1,1 атм. Визначити тиск P2 у спочатку порожньому балоні після нагрівання системи до температури t2 = 117°C.
Задача 1.22. Із рівняння Клапейрона отримати формулу густини газу \( \rho \) та знайти масу повітря (M = 29 г/моль) у кімнаті площею S = 20 м2 і висотою стелі h = 3 м при температурі t = 17 °C і атмосферному тиску P = 100 кПа.
Задача 1.23. По трубі перерізом S = 5 см2 прокачують вуглекислий газ при температурі T = 290 K і тиску P = 150 кПа. Визначити швидкість руху газу v, якщо за час t = 5 хв по трубі проходить m = 2 кг газу.
Задача 1.24. Із заданою кількістю газу \(\nu \) проводять процес, у якому тиск змінюється з температурою як $P=\alpha \sqrt{T}$, де \(\alpha \) – задана стала. Визначити залежність об'єму газу від тиску V(P) та показати її на графіку.
Задача 1.25. Повітряна куля починає підійматися при нагріванні в ній повітря до температури t = 60°C. Визначити об'єм V оболонки кулі, якщо її маса разом з вантажем складає m = 300 кг, навколишня температура T0 = 290 K і атмосферний тиск P0 = 105 Па. Молярна маса повітря M = 29 г/моль.
Задача 1.26. При підвищенні температури в повітряної кульці на k = 10 % її об'єм збільшується на n = 1 %. Визначити, на яку частку η (%) збільшується при цьому тиск повітря в кульці.
Задача 1.27. Тиск і об'єм гелію (M = 4 г/моль) масою m = 20 г лінійно змінюються від P1 = 1,55 ГПа, V1 = 12 дм3 до P2 = 0,41 ГПа, V2 = 32 дм3. Визначити максимальну температуру газу в процесі.
====================
У балоні об'ємом V = 1 л міститься m = 1 г невідомого окислу азоту NxOy при температурі t = 27 °C і тиску P = 32,8 кПа.
Встановити
хімічну формулу сполуки (визначити x та y). Газова стала R = 8,31 Дж/(моль·К).
|
Дано: NxOy
V = 1 л = 10–3 м3
m = 10–3 кг
T = 300 K
P = 3,28·104 Па
|
|
x, y - ?
|
Розв’язання
За числовими даними з рівняння Клапейрона (1.14) знаходимо молярну масу газу
\({M}=\frac{mRT}{PV}=76\cdot {{10}^{-3}}\) кг/моль,
і, знаючи його узагальнену формулу та відносні атомні маси Нітрогену A1 = 14 і Оксигену A2 = 16, складаємо числове рівняння:
\( {{M}}=x{{A}_{1}}+y{{A}_{2}}\) \( \Rightarrow\) 76 =14x+16y, або
7x + 8y = 38.
За змістом це рівняння має тільки цілочисельні розв'язки, котрі легко визначаються підбором: якщо прийняти x = 1, то y = (38 – 7)/8, чого не може бути. А ось при x = 2 маємо y = (38 – 14)/8 = 3.
Отже, шукана формула окислу — N2O3.
Задача 1.15 Балон із киснем при тиску P1 = 1 МПа і температурі t1 = 27 °C винесли надвір і підключили до газового пальника.
Визначити,
який відсоток η (%) кисню було витрачено, коли на кінець роботи тиск у балоні впав до P2 = 600 кПа при температурі t2 = –23 °C.
|
Дано: P1 = 106 Па
P2 = 6·105 Па
T1 = 300 K
T2 = 250 K
|
|
\( \eta \) - ?
|
Розв’язання
Частина використаного газу:
| \( \eta=\frac{m_{1}-m_{2}}{m_{1}}=1-\frac{m_{2}}{m_{1}}, \) | (1) |
де m1 і m2 – початкова та кінцева маси кисню в балоні, котрі визначаються з рівнянь Клапейрона (1.14). Отже:
\( \begin{align} P_{1}V=\frac{m_{1}}{M}RT_{1} \\ P_{2}V=\frac{m_{2}}{M}RT_{2} \\ \end{align}\) \( \Rightarrow \) \( \frac{P_{2}}{P_{1}}=\frac{m_{2}T_{2}}{m_{1}T_{1}}\) \( \Rightarrow \) \( \frac{m_{2}}{m_{1}}=\frac{P_{2}T_{1}}{P_{1}T_{1}}\).
Підставивши знайдене відношення (m1/m2) у вираз (1), одержимо відповідь:
\( \eta=1-\frac{P_{2}T_{1}}{P_{1}T_{2}}\) = 0,28, або \( \eta \) = 28 %.
Задача 1.16
Відкачану посудину об'ємом V = 0,5 л, що містила m = 1 г кристалічного йоду I2, нагріли до t = 1000 °C, через що він випарувався і частково дисоціював на атоми.
Визначити
частку молекул I2 , що дисоціювали, якщо в посудині встановився тиск P = 700 мм.рт.ст. Атомна маса йоду A = 127.
|
Дано: m = 10–3 кг
V = 5·10–4 м3
A = 127
P1 = 93,3 кПа
t1 = 1000 °C
|
|
\( \eta \) - ?
|
Розв’язання
З умови задачі випливає, що в посудині міститься газова суміш молекулярного (I2) та атомарного йоду (I), тиск якої за законом Дальтона дорівнює сумі парціальних тисків компонент:
P = P1 + P2.
Величини P1, P2, згідно з рівнянням Клапейрона (1.13) визначається масами компонент, як
\( {{P}_{1}}=\frac{{{m}_{1}}}{{{M}_{1}}}\frac{RT}{V};\ \ {{P}_{2}}=\frac{{{m}_{2}}}{{{M}_{2}}}\frac{RT}{V}, \)
|
|
\( {P}=\left( \frac{{{m}_{1}}}{{{M}_{1}}}+\frac{{{m}_{2}}}{{{M}_{2}}} \right)\frac{RT}{V}. \) |
(1) |
Шукана величина η дорівнює відношенню кількості N1 та маси m1 дисоційованих молекул до їхніх початкових значень N, m. Отже,
\( \frac{m_{1}}{m}=\eta \) \( \Rightarrow \) \( {m}_{1}=\eta{m}. \)
Відповідно, маса недисоційованих молекул
m2 = m – m1 \( \Rightarrow \) \( {m}_{2}=(1-\eta )m. \)
Підставляючи вирази m1 і m2 в рівняння (1) і враховуючи, що M2 = 2M1 (M1 = A·10–3 = 127·10–3 кг/моль – молярна маса атомарного йоду), одержуємо:
\( {P}=\frac{m}{M_{1}}\left(\eta+\frac{1-\eta}{2}\right)\frac{RT}{V} \),
звідки
\( \eta=\frac{2PV{{M}_{1}}}{mRT} \)–1.
Підставивши задані значення P, V, T та табличні величини М1, М2 і R, отримаємо числову відповідь:
\( \eta=12 \)%.
Задача 1.17. Відкачаний балон, який на \( \eta=0,1 \) об'єму заповнено водою, вміщають у термостат із температурою t = 300°C.
Визначити,
чи розірветься балон, якщо він витримує максимальний тиск P0 = 25 МПа?
|
Дано: \( \eta=0,1 \)
T = 573 K
P0 = 25 МПа
|
|
P - ?
|
Розв’язання
Для відповіді на поставлене запитання необхідно визначити тиск P утвореної при нагріванні балона водяної пари та порівняти його з гранично допустимою величиною P0. Тож, позначивши об'єм балона як V0, згідно з рівнянням Клапейрона (1.14), запишемо:
|
|
\( {P}=\frac{mRT}{MV_{0}}\). |
(1) |
Відтак, виразивши масу m водяної пари через густину ρ та об'єм V = ηV0 як
$m=\rho \eta {{V}_{0}}$
і врахувавши молярну масу води M = 18·10–3 кг/моль, одержимо відповідь:
\( {P}=\frac{\eta\rho{RT}}{M} \) = 26,4 МПа.
Як бачимо, P > P0, тож балон розірветься.
==============
Задача 1.18.
У балоні об'ємом V = 10 л міститься газова суміш гелію і неону загальною масою m = 36 г при тиску P = 106 Па і температура t = 28°C.
Визначити
масу гелію m1 і неону m2 в суміші.
|
Дано: V = 10–2 м3
m = 3,6·10–2 кг
P = 106 Па
Т= 301 К
|
|
m1, m2 - ?
|
Розв’язання
Відповідно до закону Дальтона (1.12)
P = P1 + P2,
де P – заданий тиск суміші, P1 і P2 – парціальні тиски гелію та неону, відповідно.
За рівнянням Клапейрона (1.13)
\( {P}_{1}=\frac{m_{1}}{M_{1}}RT, \) \( {P}_{2}=\frac{m_{2}}{M_{2}}RT, \)
тож для суміші:
|
|
\( {PV}=\left( \frac{{{m}_{1}}}{{{M}_{1}}}+\frac{{{m}_{2}}}{{{M}_{2}}} \right)RT, \) |
(1) |
Позаяк маса суміші є задана, масу якоїсь із компонент в рівнянні (1) можна виразити через масу іншої, приміром,
|
m2 = m – m1. |
(2) |
Підставивши цей вираз у рівняння (1), отримаємо:
|
|
\( {PV}=\left( \frac{{{m}_{1}}}{{{M}_{1}}}+\frac{m-{{m}_{1}}}{{{M}_{2}}} \right)RT \), |
|
і після нескладних перетворень
\( {{m}_{1}}=\left( \frac{PV}{RT}-\frac{m}{{{M}_{2}}} \right)\cdot \frac{{{M}_{1}}{{M}_{2}}}{{{M}_{2}}-{{M}_{1}}}. \)
Відтак, урахувавши молярні маси гелію M1 = 4 г/моль і неону M2 = 20 г/моль, після обчислень дістанемо
m1 = 11 г
і за співвідношенням (2)
m2 = 25 г.
При електролізі (розкладанні молекул електричним струмом) із m = 1 кг води отримано V = 710 л кисню під тиском P = 105 Па.
Визначити
температуру газу t°С.
|
Дано: m = 1 кг
V = 0,71 м3
P = 105 Па
|
|
t - ?
|
Розв’язання
За рівнянням Клапейрона (1.13) можна записати:
|
\( T=\frac{PV}{\nu_{1}R}, \) |
(1) |
де \( {{\nu }_{1}}\) – кількість кисню, що утворився. При розкладанні однієї молекули H2O утворюється один атом кисню, тобто "половина молекули" O2. Таким чином, кількість кисню \( {{\nu }_{1}}\), що утворився, дорівнює половині кількості води \( \nu \), що прореагувала:
|
|
${{\nu }_{1}}=\frac{\nu }{2}$ = $\frac{m}{2M}$, |
(2) |
де m – маса води, M = 18·10-3 кг/моль – її молярна маса. Підставивши вираз (2) в (1), одержимо відповідь:
\( {T}=\frac{2MPV}{mR}=308 \) K = 35 °C.
У кожній частині закритого вертикального циліндра із рухомим масивним поршнем заходиться по ν = 1 моль повітря.
Визначити,
за якої температури T2 відношення об'ємів повітря дорівнюватиме η2 = 3, якщо при температури T1 = 320 K воно складає η1 = 4.
|
Дано: T1 = 320 K
η1 =4
η2 = 3
|
|
T2 - ?
|
Розв’язання

Положення поршня та сили тяжіння та тиску повітря, що діють на нього, показано на рис. 20: а) при температурі T1 і б) при шуканій температурі T2.
У кожному випадку вага поршня при рівновазі компенсується різницею сил тиску повітря F = PS (S – площа поршня) по обидва боки. Отже,
|
\({{F}_{1}}-{{F}_{2}}={{{F}'}_{1}}-{{{F}'}_{2}}\quad \Rightarrow \quad {{P}_{1}}-{{P}_{2}}={{{P}'}_{1}}-{{{P}'}_{2}}\). |
(1) |
Виразивши в цьому співвідношенні тиски через температуру та об'єм за рівнянням Клапейрона (1.13) і врахувавши, що ${{V}_{2}}=\eta {{V}_{1}}$ і \({{{V}'}_{2}}={\eta }'{{{V}'}_{1}}\), після елементарних викладок отримаємо:
|
|
$\frac{T}{{{V}_{1}}}\left( 1-\frac{1}{\eta } \right)=\frac{{{T}'}}{{{V}_{1}}^{\prime }}\left( 1-\frac{1}{{{\eta }'}} \right)\quad \Rightarrow \quad \frac{{{V}_{1}}^{\prime }}{{{V}_{1}}}=\frac{{{T}'}}{T}\cdot \frac{{\eta }'\left( \eta -1 \right)}{\eta \left( {\eta }'-1 \right)}$. |
|
Звідси
|
|
${T}'=T\cdot \frac{{\eta }'\left( \eta -1 \right)}{\eta \left( {\eta }'-1 \right)}\cdot \frac{{{V}_{1}}^{\prime }}{{{V}_{1}}}$. |
(2) |
Залишається визначити величину $\left( {{V}_{1}}^{\prime }/{{V}_{1}} \right)$, що легко зробити, позаяк сумарний об'єм повітря в циліндрі не змінюється:
\( {V}_{1}+{V}_{2}=V'_{1}+V_{2}^{\prime }\) \( \Rightarrow \) \({{V}_{1}}\left( \eta +1 \right)={{V}_{1}}^{\prime }\left( {\eta }'+1 \right)\) \( \Rightarrow \) $\frac{{{V}_{1}}^{\prime }}{{{V}_{1}}}=\frac{\eta +1}{{\eta }'+1}$.
Відтак підставимо цей результат вираз (2) і отримуємо відповідь задачі:
${T}'=T\cdot \frac{{\eta }'\left( {{\eta }^{2}}-1 \right)}{\eta \left( {{{{\eta }'}}^{2}}-1 \right)}=450\ \text{K}$.
Два однакові балони, один із газом при тиску P1 = 1,0 атм і температурі t1= 27°C, а інший порожній, є сполучені трубкою з клапаном, який починає пропускати при різниці тисків у балонах ΔР ≥ 1,1 атм.
Визначити
тиск P2 у спочатку порожньому балоні після нагрівання системи до температури t2 = 117°C.
|
Дано: Т1 = 300 К
P = 1,00 атм
\( \Delta{P}\ge 1,10 \) атм
Т2 = 390 К |
|
P2 - ?
|
Розв’язання
Тиск газу в закритій посудині є прямо пропорційний температурі (рівняння (1.18)). При цьому за умовою температура збільшується в 1,3 раза (від 300 K до 390 K), а граничний тиск, який витримує клапан, є більший за початковий тільки в 1,1 раза. Тож при підвищенні температури клапан у якийсь момент відкриється, і газ буде перетікати, аж поки в балонах не встановиться критична різниця тисків \( \Delta{P}\). Отже, кінцеві тиски в балонах співвідносяться, як
|
|
\({P}_{2}={P}_{1}-\Delta{P}\). |
(1) |
Очевидним є й зв'язок між кількостями газу – початковою в першому ν та кінцевими в першому й другому ν1, ν2, відповідно:
|
\( \nu ={{\nu }_{1}}+{{\nu }_{2}}.\) |
|
Тож, визначивши ці величини через параметри стану газу за рівнянням Клапейрона (1.13) і врахувавши співвідношення (1), дістанемо:
|
$\frac{P}{{{T}_{1}}}=\frac{2{{P}_{2}}+\Delta P}{{{T}_{2}}}$, |
|
і після нескладних перетворень – відповідь задачі:
\( {{P}_{2}}=\frac{1}{2}\left( P\frac{{{T}_{2}}}{{{T}_{1}}}-\Delta P \right)=\frac{P}{2}\left( \frac{{{T}_{2}}}{{{T}_{1}}}-\frac{\Delta P}{P} \right) \) = 0,1 атм.
(Примітка. Доданок ΔP/P в дужках є безрозмірним, тож при обчисленнях немає потреби переводити значення тисків у Па).
Задача 1.22. Із рівняння Клапейрона
отримати формулу густини газу \( \rho \) та
знайти масу повітря (M = 29 г/моль) у кімнаті площею S = 20 м2 і висотою стелі h = 3 м при температурі t = 17 °C і атмосферному тиску P = 100 кПа.
|
Дано: S = 20 м2
h = 3 м
T = 290 К
P = 100 кПа
M = 2,9·10–2 кг/моль
|
|
\( \rho \), m - ?
|
Розв’язання
Густина ρ = (m/V), отже, згідно з рівнянням Клапейрона (1.14), вона визначається формулою:
\(\rho=\frac{PM}{RT}\)
і за даними задачі для повітря
ρ = 1,2кг/м3.
Тож маса повітря в кімнаті
\( {m}=\rho V=\rho Sh=72 \) кг.
Справляє враження, що, здавалося б "невагоме", повітря навіть у невеликій кімнаті має значну масу. Але, як мовиться, все пізнається в порівнянні – маса води в басейні таких самих розмірів становить 60 т !
=====
По трубі поперечним перерізом S = 5 см2 прокачують вуглекислий газ при температурі T = 290 K і тиску P = 150 кПа.
Визначити
швидкість руху газу v, якщо за час t = 5 хв по трубі проходить m = 2 кг газу.
|
Дано: CO2
S = 5·10-4 м2
T = 290 K
P = 1,5·105 Па
t = 300 с
m = 2 кг
|
|
\( {v}\) - ?
|
Розв’язання
 Виділимо в трубі подумки ділянку певної довжини l, яка вміщує масу газу m, рис. 23. При швидкості руху v весь цей газ пройде крізь передній край ділянки за час t = (l/v). Отож довжина ділянки та об'єм газу в ній складають l = vt і V = lS = Svt. Відтак, підставивши цей вираз у рівняння Клапейрона (1.14), знайдемо відповідь:
Виділимо в трубі подумки ділянку певної довжини l, яка вміщує масу газу m, рис. 23. При швидкості руху v весь цей газ пройде крізь передній край ділянки за час t = (l/v). Отож довжина ділянки та об'єм газу в ній складають l = vt і V = lS = Svt. Відтак, підставивши цей вираз у рівняння Клапейрона (1.14), знайдемо відповідь:
\( {PSvt}=\frac{m}{M}RT \) \( \Rightarrow \) \( {v}=\frac{mRT}{tPSM}. \)
Молярна маса вуглекислого газу (CO2) M = 44·10 –3 кг/моль, тож числова відповідь
\( {v}\approx{5}\) м/с.
====
Із заданою кількістю газу \(\nu \) проводять процес, у якому тиск змінюється з температурою як \(P=\alpha {{T}^{1/2}}\), де \(\alpha \) – задана стала.
Визначити
залежність об'єму газу від тиску V(P) та показати її на графіку.
|
Дано: \(\nu \) = const
\(P=\alpha {{T}^{1/2}}\)
\(P_{2}/P_{1}=k\)
k = 2
|
|
V(Р) - ?; V2/V1 - ?
|
Розв’язання
Шукану залежність об'єму газу від тиску V(P) отримаємо з рівняння Клапейрона (1.13), виразивши в ньому температуру T через тиск P , відповідно до умови задачі:
$PV=\nu R\cdot {{\left( {P}/{\alpha }\; \right)}^{2}}\quad \Rightarrow \quad V=\beta P,\quad \beta =\left( {\nu R}/{{{\alpha }^{2}}}\; \right)$.
Графік V(P) показано на рис. 24.
 |
Отже, виходить, що при стисненні газ розширюється. Але цей "парадокс" є удаваним, бо стиснення (збільшення тиску) забезпечується не рухом поршня, а нагріванням газу.
=====
Повітряна куля починає підійматися при нагріванні в ній повітря до температури t = 60 °C.
Визначити
об'єм V оболонки кулі, якщо її маса разом з вантажем складає m = 300 кг, навколишня температура T0 = 290 K і атмосферний тиск P0 = 105 Па. Молярна маса повітря M = 29 г/моль.
|
Дано: Т = 333 К
m = 300 кг
T0 = 290 K
P0 = 105 Па
M = 2,9·10–2 кг/моль
|
|
\( {V}\) - ?
|
Розв’язання
 Підйом кулі почнеться, коли виштовхувальна сила FA навколишнього повітря зрівноважить силу тяжіння FT (рис. 25), величина котрої
Підйом кулі почнеться, коли виштовхувальна сила FA навколишнього повітря зрівноважить силу тяжіння FT (рис. 25), величина котрої
|
FT = mg + ρVg, |
|
де m – маса оболонки кулі з вантажем, ρVg – маса повітря всередині при густині ρ і об'ємі оболонки V. Відповідно, виштовхувальна сила дорівнює вазі навколишнього повітря в об'ємі оболонки (закон Архімеда), котре має густину ρ0 :
|
|
FА = ρ0Vg. |
|
Отже, умовою підйому кулі є рівність:
\({{\rho }_{0}}Vg=mg+\rho Vg\) ,
з якої для шуканого об'єму оболонки виходить формула
|
|
\(V=\frac{m}{{{\rho }_{0}}-\rho }.\) |
(1) |
Густини повітря за рівнянням Клапейрона (1.14) визначаються, як
\(\rho =\frac{{{P}_{0}}M}{RT}\) і ${{\rho }_{0}}=\frac{{{P}_{0}}M}{R{{T}_{0}}}$.
Тож, підставивши ці вирази у формулу (1), дістанемо відповідь задачі:
\(V=\frac{mR{{T}_{0}}T}{{{P}_{0}}M(T-{{T}_{0}})}\approx 1930\) м3.
====
При підвищенні температури в повітряної кульці на k = 10 % її об'єм збільшується на n = 1 %.
Визначити,
на яку частку η (%) збільшується при цьому тиск повітря в кульці.
|
Дано: k = 10 %
n = 1 %
|
|
\(\eta\) - ?
|
Розв’язання
Зміна параметрів стану повітря в кульці відбувається при незмінній кількості, тож, згідно з рівнянням Клапейрона (1.14), параметри початкового (P1, V1, T1) та кінцевого (P2, V2, T2) стану пов'язані співвідношенням:
|
|
\(\frac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}}.\) |
(1) |
При цьому за умовою задачі
|
|
\(\begin{align} & {{V}_{2}}={{V}_{1}}+\Delta V={{V}_{1}}+n{{V}_{1}}=V(1+n), \\ & {{T}_{2}}={{T}_{1}}+\Delta T={{T}_{1}}+n{{T}_{1}}=T(1+k). \\\end{align}\) |
(2) |
По аналогії те саме можна записати й для тисків :
|
|
\({P}_{2}={P}_{1}+\Delta P={P}_{1}+\eta{P}_{1}=P(1+\eta).\) |
(3) |
Підставивши вирази (2), (3) у співвідношення (1), одержуємо відповідь:
\(\frac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{1}}(1+\eta){{V}_{1}}(1+n)}{{{T}_{1}}(1+k)}\) \( \Rightarrow \) \( 1+\eta=\frac{1+k}{1+n}\) \(\Rightarrow \) \(\eta=\frac{1+k}{1+n}-1.\)
Обчислення дають
\(\eta=0,089=8,9\) %.
Задача 1.27.
Тиск і об'єм гелію (M = 4 г/моль) масою m = 20 г лінійно змінюються від P1 = 1,55 ГПа, V1 = 12 дм3 до P2 = 0,41 ГПа, V2 = 32 дм3.
Визначити
максимальну температуру газу в процесі.
|
Дано: M = 4·10–3 кг/моль m = 2·10–2 кг P1 = 1,55·109 Па V1 = 1,2·10–2 м3 P2 = 4,1·108 Па V2 = 3,2·10–2 м3 |
|
Tm - ? |
Розв’язання
На рис. 27 показано графік заданої в умові залежності P(V), згідно з яким
|
$P={{P}_{0}}-\alpha V$ , |
(1) |
де
|
$\alpha =\frac{{{P}_{1}}-{{P}_{2}}}{{{V}_{2}}-{{V}_{1}}}$. |
(2) |
Підставивши вираз (1) у рівняння Клапейрона (1.13), наступну залежність температури газу від об'єму:
|
$T=\frac{M}{mR}\left( {{P}_{0}}V-\alpha {{V}^{2}} \right)$. |
Її графіком є відрізок параболи, розташований між точками V = 0 і V = V0. Отже, максимум температури газу в заданому процесі спостерігається при V = (V0/2), P = (P0/2) і, згідно з (1.14), складає
|
${{T}_{max}}=\frac{M}{4mR}{{P}_{0}}{{V}_{0}}$. |
(3) |
Величини V0, P0 легко знаходяться з рис. 1.27 через коефіцієнт α:
|
$\frac{{{P}_{0}}-{{P}_{1}}}{{{V}_{1}}}=\frac{{{P}_{1}}-{{P}_{2}}}{{{V}_{2}}-{{V}_{1}}}\quad \Rightarrow \quad {{P}_{0}}=\frac{{{P}_{1}}{{V}_{2}}-{{P}_{2}}{{V}_{1}}}{{{V}_{2}}-{{V}_{1}}}$, |
|
$\frac{{{P}_{2}}}{{{V}_{0}}-{{V}_{2}}}=\frac{{{P}_{1}}-{{P}_{2}}}{{{V}_{2}}-{{V}_{1}}}\quad \Rightarrow \quad {{V}_{0}}=\frac{{{P}_{1}}{{V}_{2}}-{{P}_{2}}{{V}_{1}}}{{{P}_{1}}-{{P}_{2}}_{1}}$. |
Відтак, підставивши ці значення у вираз (3), отримаємо загальну відповідь:
${{T}_{max}}=\frac{M}{4nR}\cdot \frac{{{\left( {{P}_{1}}{{V}_{2}}-{{P}_{2}}{{V}_{1}} \right)}^{2}}}{\left( {{P}_{1}}-{{P}_{2}} \right)\left( {{V}_{2}}-{{V}_{1}} \right)}$,
або після обчислень
Тm = 417 К = 144°С.
Ізопроцеси (газові закони)
Задача 1.28. При ізотермічному стисканні ν = 1 моль газу на ΔP =300 кПа його об'єм змінюється від V1 = 10 л до V2 = 4 л. Визначити температуру газу t°С.
Задача 1.29. Повітря у відкритому вертикальному циліндрі під рухомим поршнем нагрівають від температури t1= 7°С до t2= 63°С. Атмосферний тиск P = 760 мм.рт.ст., площа основи циліндра S = 100 см2. Визначити: 1. Відстань h, на яку переміститься поршень, якщо спочатку він перебував на відстані l = 30 см від основи циліндра. 2. Масу гирі m, яку треба покласти на поршень, аби повернути його в початкове положення при незмінній температурі повітря.
Задача 1.30. Показати, як зміниться ізотерма(графік залежності P(V) при T = const, якщо: а) при незмінній масі m відомого газу підвищити його температуру T; б) при незмінній температурі T відомого газу збільшити його масу m; в) при тих самих масі m та температурі T провести процес із газом більшої молярної маси M.
Задача 1.31. Із газом в циліндрі під рухомим поршнем проводять комбінований процес 1→2→3, в якому газ на ділянці 1→2 нагрівається, а на ділянці 2→3 повертається до вихідної температури так, як показано на рис. 31 у розв'язанні. За заданою залежністю тиску від температури P(T) проаналізувати зміну об'єму газу з температурою і знайти відношення його значень (V1/V3) у початковому та кінцевоому стані, якщо відношення тисків (P1/P3) = 2.
Задача 1.32. Із заданою кількістю газу проводять замкнений процес, який на діаграмі P-V зображується колом. Проаналізувати зміну температури газу в цьому процесі та позначити на графіку точки, що відповідають найнижчій Tmin і найвищій Tmax температурі газу..
Задача 1.33. Із газом у циліндрі під поршнем проведено заданий цикл 1→2→3→ 4→1 (рис. 33 у розв'язянні), в якому ділянки 2→3 і 4→1 є ізотермами, і об'єм в точках 1 і 3 має задану величину V1 і V3. Визначити об'єм газу V в точках 2, 4.
Задача 1.28. При ізотермічному стисканні ν = 1 моль газу на ΔP =300 кПа його об'єм змінюється від V1 = 10 л до V2 = 4 л.
Визначити
температуру газу t°С.
|
Дано: ν = 1 моль V1 = 10–2 м3 V2 = 4·10–3 м3 ΔP =3·105 Па |
|
t - ? |
Розв'язання
Якщо позначити початковий тиск газу як P1, а кінцевий – як P2, то
P2 = P1 + ΔP.
Тож за законом Бойля-Маріотта (1.16а)
${{P}_{1}}{{V}_{1}}=\left( {{P}_{1}}+\Delta P \right){{V}_{2}}\quad \Rightarrow \quad {{P}_{1}}=\frac{{{V}_{2}}\Delta P}{{{V}_{1}}-{{V}_{2}}}$.
Відтак підставимо цей вираз у рівняння Клапейрона (1.13) і одержимо відповідь:
$T=\frac{\Delta P{{V}_{1}}{{V}_{2}}}{\nu R\left( {{V}_{1}}-{{V}_{2}} \right)}$ ≈ 241 К $\Rightarrow $ t = –32°С.
Задача 1.29. Повітря у відкритому вертикальному циліндрі під рухомим поршнем нагрівають від температури t1= 7°С до t2= 63°С. Атмосферний тиск P = 760 мм.рт.ст., площа основи циліндра S = 100 см2.
Визначити:
1. Відстань h, на яку переміститься поршень, якщо спочатку він перебував на відстані l = 30 см від основи циліндра.
2. Масу гирі m, яку треба покласти на поршень, аби повернути його в початкове положення при незмінній температурі повітря.
|
Дано: Т1= 280 К Т2= 336 К P = 105 Па S = 10–2 м2 l = 0,3 м |
|
h - ?, m -? |
Розв'язання
1. З умови зрозуміло, що нагрівання повітря відбувається при сталому тиску P. Тому, відповідно до закону Гей-Люссака (1.17а),
|
$\frac{{{V}_{2}}}{{{V}_{1}}}=\frac{{{T}_{2}}}{{{T}_{1}}}\quad \Rightarrow \quad \frac{{{l}_{2}}}{{{l}_{1}}}=\frac{{{T}_{2}}}{{{T}_{1}}}$, |
|
де V1, V2 – початковий і кінцевий об'єми повітря, і відстані l1 = l, l2 = l + h. Отже,
$\frac{l+h}{l}=\frac{{{T}_{2}}}{{{T}_{1}}}\quad \Rightarrow \quad h=l\left( \frac{{{T}_{2}}}{{{T}_{1}}}-1 \right)=6\text{см}\text{.}$
2. Покладена гиря створює додатковий тиск на поршень P′ = (mg/S), через що тиск і об'єм нагрітого повітря ізотермічно змінюються відповідно від значень P і (l + h)S до (P1 +P′) і (l S). Тож за законом Бойля-Маріотта (1.16а),
${{P}}\left( {{l}}+h \right)=\left( {{P}}+\frac{mg}{S} \right){{l}}\quad \Rightarrow \quad m=\frac{{{P}}S}{g}\cdot \frac{h}{{{l}}}$ = 20 кг.м.====
Показати,
як зміниться графік залежності P(V) при T = const (ізотерма), якщо: а) при незмінній масі m заданого газу підвищити його температуру T; б) при незмінній температурі T заданого газу збільшити його масу m; в) при тих самих масі m та температурі T провести процес із газом більшої молярної маси M.
Розв’язання
В ізотермічному процесі (ν = const, T = const) залежність P(V) між тиском і об'ємом газу визначається рівнянням (1.16):
\( P=\frac{a}{V},\)
де a = (mRT/M) = const. Отже, ізотерма має форму гіперболи, положення котрої відносно координатних осей визначається коефіцієнтом a: чим він більший, тим вище розташовується графік P(V). Це схематично показано на рис. 30, де в кожному випадку зеленим кольором зображено вихідну ізотерму, а червоним – ізотерму для зміненого значення указаного параметра стану газу.
Із газом в циліндрі під рухомим поршнем проводять комбінований процес 1→2→3, в якому газ на ділянці 1→2 нагрівається, а на ділянці 2→3 повертається до вихідної температури, як показано на рис. 31. За заданою залежністю тиску від температури P(T)
проаналізувати зміну об'єму газу з температурою і знайти відношення його значень (V1/V3) у початковому та кінцевому стані, якщо відношення тисків (P1/P3) = 2.
|
Дано: (P1/P3) = 2 |
|
(V1/V3) -? |
Розв’язання

На кожній з ділянок заданого процесу об'єм газу неперервно змінюється. Тому для встановлення кількісного зв'язку між об'ємом і температурою слід було би спочатку для кожної ділянки графіка рис. 31 встановити математичну залежності P(T), а потім, підставивши її в рівняння (1.13), визначити залежність V(T) і знайти відношення (V1/V3).
Проте відповідь можна отримати простіше методом "ізоперетинів", котрий ґрунтується на об'єднаному газовому законі (1.15) й полягає в наступному. Коли графіки для якоїсь пари параметрів у двох процесах із однаковою кількістю газу перетинаються, то в точці перетину збігаються значення й третього параметра. Тож, якщо через відповідні точки заданого графіка P(T) провести ізохори (штрихові промені на рис. 31), то позаяк при переході 1 → 2 нахил ізохори стає меншим, а при переході 2→3 більшим, то об'єм газу, навпаки, спочатку зростає, а потім зменшується. При цьому за умовою Т1= Т3 і (P1/P3) = 2, тож, відповідно до рівняння (1.15), шукане відношення об'ємів складає
$\frac{{{V}_{1}}}{{{V}_{3}}}=\frac{1}{2}$.
Але найпростіше знайти відповідь можна, врахувавши, що за умовою маємо під поршнем однакову кількість газу при однакових початковій та кінцевій температурі. Це означає, що точки 1 і 3 на рис. 31 належать одній ізотермі, тож за законом Бойля-Маріотта (1.16 б)
$\frac{{{V}_{1}}}{{{V}_{3}}}=\frac{{{P}_{3}}}{{{P}_{1}}}=\frac{1}{2}$.
Задача 1.32. Із заданою кількістю газу проводять замкнений процес, який на діаграмі P-V зображується колом. Проаналізувати зміну температури в цьому процесі та
позначити на графіку точки,
що відповідають найнижчі1 Tmin і найвищій Tmax температурі газу.
Розв’язання

Ця задача розв'язується аналогічно до попередньої. Розсічемо графік заданого процесу сімейством ізотерм (a - d) так, аби крайні дотикалися до графіка P(V), рис. 32. Тоді, як випливає із закону Бойля-Маріотта (1.16), точки дотику відповідають мінімальній (1) та максимальній (2) температурі. Тож
на ділянці 1→2 газ нагрівається, а на ділянці 2→3 охолоджується.
Задача 1.33. Із газом у циліндрі під поршнем проведено  заданий цикл 1→2→3→ 4→1 (рис. 33), в якому ділянки 2→3 і 4→1 є ізотермами, і об'єм в точках 1 і 3 має задану величину V1 і V3.
заданий цикл 1→2→3→ 4→1 (рис. 33), в якому ділянки 2→3 і 4→1 є ізотермами, і об'єм в точках 1 і 3 має задану величину V1 і V3.
Визначити
об'єм газу V в точках 2, 4.
|
Дано: V1 ,V3 |
|
V -? |
Розв’язання
Як видно із заданого графіка рис. 33, V2 = V4 =V, тож можна записати
|
$\frac{{{P}_{1}}}{{{P}_{2}}}=\frac{{{V}_{1}}}{V}\quad \Rightarrow \quad {{P}_{1}}V={{P}_{2}}{{V}_{1}}$, |
(1) |
|
$\frac{{{P}_{4}}}{{{P}_{3}}}=\frac{V}{{{V}_{3}}}\quad \Rightarrow \quad {{P}_{3}}V={{P}_{4}}{{V}_{3}}$. |
(2) |
А за законом Бойля-Маріотта (1.16а)
|
${{P}_{4}}V={{P}_{1}}{{V}_{1}}$, |
(3) |
|
${{P}_{2}}V={{P}_{3}}{{V}_{3}}$. |
(4) |
Відтак, перемноживши ліві й праві частини рівнянь (1)-(4), дістанемо:
${{V}^{4}}={{\left( {{V}_{1}}{{V}_{3}} \right)}^{2}}\quad \Rightarrow \quad V=\sqrt{{{V}_{1}}{{V}_{3}}}$.
+
3. Задачі для самостійної роботи
Розв'язуючи задачі, слід пам'ятати про таке.
В умовах задач усі гази по замовчуванню вважаються ідеальними.
Маси атомів і молекул зазвичай задаються в а.о.м., тоді як при обчисленнях вони мають виражатися в натуральних мірах (кілограм, грам, тощо).
Так само в текстах температура зазвичай задається в °С, а у формулах фігурує абсолютна температура (К).
У відповідях пропонованих задач для нормального атмосферного тиску прийнято 100 кПа і для g = 10 м/с2.
Визначаючи характеристики атомів і молекул, звертайте увагу на порядки величин. Так ви краще відчуєте масштаби мікросвіту та застрахуєтеся від грубих похибок у обчисленнях.
Наведені далі задачі для вправ за рівнем складності поділено на групи А, В, і С.
Характеристики молекул
|
1.34. |
Обчислити масу однієї молекули озону (O3), вуглекислого газу (CО2) і метану (CH4). [8,0·10–26 кг; 7,3·10–26 кг; 2,7·10–26 кг]. |
|
1.35. |
Обчислити кількість молекул, що містяться в 1 мл води. Визначити масу й оцінити розмір однієї молекули. [3,3·1022; 3·10–26 кг; 3·10–10 м]. |
| 1.36. |
За 10 діб зі склянки випарувалося 100 мл води. Скільки молекул у середньому випаровувалося за 1 с? [4·1018]. |
|
1.37. |
Визначити концентрацію молекул (1/см3) при температурі 17°С у посудині, відкачаній до глибокого вакууму з тиском повітря 10–8 Па. [2,5·106 1/см3]. |
|
1.38. |
При температурі 10°С енергія молекул одного моля газу складає 3,5 кДж. Визначити середню енергію однієї молекули при температурі 100°С. [5,8·10–20 Дж]. |
|
1.39. |
Визначити температуру газу, якщо середня кінетична енергія однієї його молекули складає 2,6·10–20 Дж. [983°С]. |
|
1.40. |
Визначити середню квадратичну швидкість броунівського руху крапельки води радіусом 1 мкм, яка є зважена ("плаває") в повітрі при температурі 17°С. [1,7 мм/с]. |
|
1.41. |
Визначити, як зміниться тиск газу при збільшенні його об'єму та середньої кінетичної енергії однієї молекули в 2 рази? [Не зміниться]. |
|
1.42. |
В кімнаті об'ємом 60 м3 розприскали 100 мг парфуму з відносною молекулярною масою 106. Визначити кількість його молекул в 1 л повітря. [2·1016]. |
|
1.43. |
В озеро площею 100 км2 і середньою глибиною 20 м, кинули крупинку харчової солі NaCl масою 10 мг. Уявивши, що її компоненти рівномірно розподілилися по всьому об'єму озера, визначити їхню кількість у склянці взятої з нього води об'ємом 200 мл. [2·107]. |
Рівняння стану ідеального газу
Рівень А
|
1.44. |
Обчислити об'єм одного моля газу за нормальних умов (0°С, 760 мм.рт.ст). [22,4 л]. |
||
|
1.45. |
Визначити кількість молекул повітря в колбі об'ємом 0,5 дм3 за нормальних умов. [1,33·1022] |
||
|
1.46. |
14 г азоту в балоні об'ємом 10 л створюють тиск 125 кПа. Визначити температуру газу. [27°С]. |
||
|
Який об'єм займають 11 г вуглекислого газу за нормальних умов? [5,6 л]. |
||
|
1.48. |
Газ масою 14 г міститься в балоні об'ємом 0,5 л при температурі 127°С і тиску 125 кПа. Визначити молярну масу газу. [2 г/моль]. |
||
| 1.49. |
Знайти температуру кисню, що при тиску 0,2 МПа має густину 1,2 кг/м3. [369°С]. |
||
| 1.50. |
В балоні об'ємом 110 л міститься 8 г водню і 14 г азоту. Визначити тиск суміші на стінки балона при температурі 27°С. [100 кПа]. |
||
| 1.51. |
Визначити, на скільки відрізняється маса повітря в приміщенні об'єм 50 м3 при атмосферному тиску 100 кПа взимку за температури 0°С та влітку при 40°С . Молярна маса повітря 29 г/моль. [8,2 кг]. |
||
| 1.52. |
При температурі 15°С водень має тиск 135 кПа і займає об'єм 2 л. Газ стисли до об'єму 1,5 л і нагріли до температури 30°С. Визначити кінцевий тиск газу. [190 кПа]. |
||
|
Рівень Б |
|||
| 1.53. |
Через витік водню з балона місткістю 10 л, при нагріванні від 7°С до 17°С тиск газу лишився незмінним і рівним 5 МПа. Скільки молекул вийшло з балона за цей час? [4,46·1023]. |
||
| 1.54. |
Після випускання деякої кількості газу тиск у балоні впав на 40%, а температура знизилася на 10 К. Яка частину газу було випущено? [1/3] |
||
| 1.55. |
В балоні об'ємом 10 л міститься повітря за нормальних умов. При закачуванні ще деякої кількості повітря тиск у балоні збільшився в 1,2 раза, а температура зросла на 7°С . Знайти масу доданого повітря. [2,2 г]. |
||
| 1.56. |
Визначити енергію теплового руху молекул одного моля кисню в балоні об'ємом 6 л при тиску 100 кПа. [900 Дж]. |
||
| 1.57. |
Показати, що за сталого атмосферного тиску сумарна кінетична енергія молекул повітря в приміщенні не залежить від температури. |
||
| 1.58. |
|
||
| 1.59. |
Дві посудини з’єднані тонкою трубкою з краном. В одній посудині міститься 1,5 л азоту під тиском 400 кПа, а в другій – 3 л кисню під тиском 250 кПа . Визначити тиск, який встановиться в посудинах, якщо відкрити кран. Температура не змінюється. [300 кПа]. |
||
| 1.60. |
У посудині об'ємом 20 л міститься суміш водню й гелію при температурі 16°С і тиску 2 атм. Маса суміші 5 г. Визначити співвідношення мас водню й гелію в суміші. [1:2]. |
||
| 1.61. |
|
||
Ізопроцеси
Рівень А
|
1.62. |
Посудину з повітрям об'ємом 4,5 л відкачують поршневим насосом з робочим об'ємом камери 500 см3. Визначити, на скільки відсотків зменшується тиск у посудині за один хід поршня при незмінній температурі. [10%]. |
|
1.63. |
У закріпленому горизонтальному циліндрі з рухомим поршнем діаметром 10 см міститься повітря. Визначити атмосферний тиск, якщо для зменшення об'єму повітря в циліндрі вдвічі до поршня довелося прикласти силу 770 Н. [98 кПа]. |
|
1.64. |
У циліндрі під рухомим поршнем міститься 10 л газу з температурою 50°С. Знайти об'єм газу після охолодження до 0°С. [≈8,5 л]. |
|
1.65. |
Повітряну кульку об'ємом 2 дм3 знадвору при температурі повітря 2°С внесли в кімнату з температурою 27°С. Визначити, яким став об'єм кульки. [≈2,2 дм3]. |
|
1.66. |
Довести, що для ідеального газу коефіцієнт об'ємного розширення та температурний коефіцієнт тиску є однакові й складають (1/273) 1/К. |
|
1.67. |
Гази при температурі 900°С виходять із плавильної печі в навколишнє середовище й при сталому тиску охолоджуються до 20°С. Визначити, в скільки разів зменшується їхній об'єм. [ 4 ]. |
|
1.68. |
Газ у балоні перебуває під тиском 16,5 МПа при температурі 50°С. Знайти, яким стане тиск у балоні після охолоджування газу до 20°С. [15 МПа]. |
|
1.69. |
Із двома різними газами з відомими масами m1, m2 та молярними масами M1,M2, проводять |
| 1.70. |
Із газом маси m1 і молярної маси M1 проводять ізобарний процес при тиску P1. Проаналізувати та показати на одній діаграмі залежності V(T) при вказаних параметрах і при при зміненому значенні одного з них: а) P2 > P1; б) m2 > m1; в) M2 > M1. [див. рис.] |
Рівень Б
|
1.71. |
Якщо горизонтальний циліндр із рухомим поршнем площею 25 см2 поставити вертикально, об'єм повітря в ньому зміниться на 10%. Визначити масу поршня. Атмосферний тиск 100 кПа. [2, 25 кг, або 2,75 кг]. |
|
1.72. |
Коли на поршень у вертикальному циліндрі з газом поклали тягар масою 1,5 кг, об'єм повітря в ньому зменшився в 4 рази. Визначити масу тягаря, який треба додатково покласти на поршень, аби зменшити об'єм повітря в циліндрі ще в 2 рази. [2 кг]. |
|
1.73. |
У лабораторній роботі з визначення атмосферного тиску запаяну з одного кінця скляну трубку довжини L = 60 см занурюють у циліндр з водою на глибину H = 40 см й вимірюють висоту h стовпчика води, що зайшов у трубку. Вивести розрахункову формулу та обчислити результат досліду P0 (мм.рт.ст.), якщо h = 21 мм. (g = 9,8 м/с2, 1 мм.рт.ст. = 133,3 Па). \(\left[ {{P}_{0}}=\frac{\rho g}{h}\left( L-h \right)\left( H-h \right) \right]\) = 768 мм.рт.ст. |
| 1.74. |
До балона об'ємом 10 л приєднано поршневий насос із робочим об'ємом камери 0,5 л. Визначити, за скільки ходів поршня тиск повітря в балоні: а) збільшиться та б) зменшиться вдвічі. Температуру повітря вважати сталою. [а) 10; б) 7,3]. |
| 1.75. |
Вертикальний циліндр із повітрям при тиску P0 = 100 кПа й температурі t0= 0°С у верхній основі має отвір площею 1 см2, який щільно накрито кришкою маси 300 г. Визначити температуру, до якої слід нагріти повітря в циліндрі, аби воно почало виходити назовні? [82°С]. |
| 1.76. |
При підвищенні температури газу в закритому циліндрі на 75°С його тиск збільшився на 25%. Визначити початкову температуру газу. [27°С]. |
| 1.77. |
Порожню пляшку закоркували надворі при температурі повітря –23°С й занесли до кімнати з температурою 27°С . Визначити, чи втримається корок у пляшці, якщо площа його перерізу 3 см2 і максимальна сила тертя спокою між ним і пляшкою 25 Н. Атмосферний тиск 100 кПа. [Ні]. |
| 1.78. |
Коли на рухомий поршень у циліндрі поклали вантаж масою M, об'єм газу зменшився в n разів. Якої маси вантаж треба додати, аби об'єм газу зменшився знов у n разів? [nM]. |
| 1.79. |
Циліндр висотою 50 см і площею основи 100 см2, перекритий рухомим поршнем маси 10 кг, підвішено на шнурі. При цьому нижня поверхня поршня знаходиться на відстані 4 см від краю циліндра. Визначити, чи утримається поршень у циліндрі після перерізання шнура. [Ні]. |
Розділ ІІ. Перший закон термодинаміки
В молекулярній фізиці поряд із молекулярно-кінетичною теорією застосовують термодинамічний метод дослідження. Цей метод ґрунтується на тому, що між фізичними характеристиками будь-якої системи існують такі функціональні зв'язки, які не залежать від особливостей молекулярної будови системи та індивідуальних властивостей молекул.
Фундамент термодинаміки складають універсальні закони (начала) термодинаміки. Вони базуються на дослідних фактах і мають вичерпне обґрунтування в молекулярно-кінетичній теорії.
Далі розглянуто наступне.
Колові процеси, теплові двигуни
2.1.Термодинамічні величини
При розгляді процесів у молекулярній системі як цілому, крім тиску, об'єму та температури, використовують відповідні термодинамічні (інакше макроскопічні) величини, як от внутрішня енергія, робота та кількість теплоти.
Внутрішня енергія U складається із сумарної кінетичної енергії теплового руху молекул тіла та потенціальної енергії їхньої взаємодії між собою й не залежить від руху тіла як цілого та дії на нього з боку інших тіл.
В ідеальному газі взаємодія між молекулами на відстані відсутня, тож його внутрішня енергія
$U=\sum{{{E}_{i}}=N\left\langle E \right\rangle }$,
де Ei – кінетичні енергії теплового руху окремих молекул, \( \left\langle E \right\rangle \) – середня кінетична енергія однієї молекули, N – загальна кількість молекул у газі.
Згідно з формулами (1.3) та (1.8), внутрішню енергію ідеального газу можна виразити через його температуру як
|
|
\( {U}=\frac{3}{2}\nu RT \) або \( {U}=\frac{3}{2}\cdot \frac{m}{M}RT \), |
(2.1) |
де m, M – маса молекули та молярна маса газу, T – температура, ν = (m/M) – кількість газу (моль), R = N0k – універсальна газова стала. Враховуючи рівняння Клапейрона (1.13, 1.14), внутрішню енергію газу можна виразити також через тиск та об'єм:
|
|
\( {U}=\frac{3}{2}PV \). |
(2.2) |
Примітка. Формули (2.1), (2.2), як і (1.3), (1.8), див. п. 1.1, строго говорячи, відносяться тільки до одноатомних газів. Але в елементарній фізиці їх застосовують для всіх зазів, уважаючи їхні молекули матеріальними точками.
При переході газу із стану 1(P1, V1, T1) у стан 2(P2, V2, T2) зміна його внутрішньої енергії визначається зміною параметрів стану:
|
|
\( {{U}_{2}}-U_{1}^{{}}=\frac{3}{2}\cdot \frac{m}{M}R({{T}_{2}}-{{T}_{1}})=\frac{3}{2}\cdot \frac{m}{M}R\Delta T \) |
(2.3) |
або
|
|
\( {{U}_{2}}-{{U}_{1}}=\frac{3}{2}\cdot ({{P}_{2}}{{V}_{2}}-{{P}_{1}}{{V}_{1}}) \). |
(2.4) |
Тож із формул (2.1) – (2.4) випливає, що
кожному станові ідеального газу відповідає визначена внутрішня енергія, причому її зміна не залежить від виду процесу, тобто способу переходу газу від початкового до кінцевого стану.
(Зворотнє не має місця – заданому значенню U відповідає безліч різних комбінацій параметрів P і V, тобто різних станів).
Сказане є чинним не лише для газів, а й для будь-яких інших фізичних систем, тому говорять, що
|
внутрішня енергія є функцією стану системи |
Ще одна універсальна властивість внутрішньої енергії полягає в тому, що
|
внутрішня енергія системи є прямо пропорційна до температури. |

До прикладу, при ізобарному розширенні газу в циліндрі поршень переміщується на деяку відстань \( \Delta{x}\) (рис. 2.1), і сила тиску газу F = PS виконує роботу
|
|
\( \Delta{A}=P\Delta{V}\), |
(2.5) |
де P – тиск газу, \( \Delta{V}=S\Delta{x}\) – зміна його об'єму. При цьому газ у цілому лишається нерухомим. Таким чином,
термодинамічна робота визначається не рухом тіла, а зміною його об'єму.
Тут, як і в попередньому розділі (п. 1.3), розглядаються рівноважні процеси в газах. Тож рух поршня вважається настільки повільним, що в кожен момент часу сили F′ і F є практично однаковими. За такої умови їхні роботи відрізняються лише знаком:
|
|
\( \begin{align} & \Delta {A}'=-\Delta A, \\ & \Delta {A}'=-P\cdot \Delta V \\ \end{align}\). |
(2.5а) |
Зокрема, при стисканні зовнішня сила виконує додатню, а газ – таку саму від'ємну роботу.
У довільному процесі при зміні об'єму газу змінюється й тиск, тож у загальному випадку наведені формули для прямого обчислення роботи через зміну об'єму є непридатні. Проте при гранично малих значеннях ΔV формули (2.5), (2.5а) зберігають чинність, та їхнє застосування вимагає використання методів вищої математики. Втім для якісного аналізу (а інколи й для обчислень) може стати в пригоді графік процесу на діаграмі (P, V), рис. 2.2.

Справді, з рис.2.2а зрозуміло, що елементарна робота газу \( \Delta{A}=P\cdot\Delta{V}\) чисельно дорівнює площі виділеної вузької смужки шириною \( \Delta{V}\), а повна робота – площі SPV під усім графіком процесу:
|
|
A = SPV. |
(2.6) |
При лінійній залежності P(V) ця площа легко знаходиться. До прикладу, в ізобарному процесі (рис.8.2б) P = const, і з графіка маємо
|
|
A = P(V2 – V1), |
(2.7) |
як і за формулою (2.5).
Враховуючи рівняння Клапейрона (1.14), роботу газу в ізобарному процесі можна виразити й через зміну температури:
|
|
\( {A}=\frac{m}{M}R({{T}_{1}}-{{T}_{2}})=\frac{m}{M}R\cdot \Delta T \). |
(2.8) |
Зокрема, при (m/M)= 1 моль і \( \Delta{T}=1 \) K виходить A = R (Дж), отже,
|
універсальна газова стала чисельно дорівнює роботі одного моля ідеального газу при ізобарному нагріванні на 1 К. |
Варто звернути увагу й на те, що на відміну від внутрішньої енергії, робота при зміні стану газу залежить не тільки від величини зміни параметрів стану, але й від того, як вона відбувалася. Це можна зрозуміти з рис. 2.2а: при однакових початкових і кінцевих параметрах стану в процесі, що зображений кривою синього кольору, газ виконує більшу роботу, ніж у зображеному зеленим. Тому говорять, що
|
робота газу є функцією процесу. |
Наведені міркування й формули (крім (2.8)), є чинні не тільки для газів, а й для рідин і твердих тіл. Але в них термічне розширення та стискуваність є значно слабшими, тож робота теплового розширення в твердих тілах і рідинах зазвичай є неістотною.
Теплообмін. Кількість теплоти. Стан термодинамічної системи та її внутрішня енергія можуть змінюватись і через теплообмін. Цим терміном означають
процеси переходу енергії від одних тіл до інших без виконання роботи.
Існують різні види теплообміну: теплопередача, коли обмін енергією відбувається при безпосередньому контакті тіл (нагрівання на плиті каструлі з водою), конвекція (переміщення потоків газу або рідини з різними температурами внаслідок різниці густин) променистий або радіаційний теплообмін завдяки випромінюванню нагрітими тілами теплової енергії. До теплообміну також відносяться процеси виділення та поглинання енергії при хімічних реакціях або зміні агрегатного стану речовини.
Кількісною характеристикою процесів теплообміну є
кількість теплоти – фізична величина, рівна енергії, що отримана чи віддана тілом без виконання роботи.
Зрозуміло, що кількість теплоти, як і енергія, вимірюється в джоулях (Дж), але в даному контексті джоуль є кількісною мірою не енергії як такої, а її зміни в певному процесі. Тому не можна говорити про кількість теплоти в тілі. Так само кількість теплоти, отримана системою, визначається не самою зміною її стану, а способом цієї зміни, тобто процесом, який відбувся в системі.
Наостанку згадаємо, що кількість теплоти трактується як алгебраїчна величина, тож, якщо система внаслідок теплообміну втрачає енергію, то формально вона отримує від'ємну кількість теплоти.
Перший закон термодинаміки
Термодинамічні величини підпорядковуються відповідним основним законам. В елементарній фізиці детально розглядається тільки перший закон термодинаміки, який гласить:
зміна внутрішньої енергії U довільної системи дорівнює сумі отриманої нею кількості теплоти Q та виконаної над системою роботи \({A}' \) зовнішніх сил:
|
|
\( {{U}_{2}}-{{U}_{1}}=Q+{A}' \) або \( \Delta U=Q+{A}' \) |
(2.9) |
і по суті виражає закон збереження енергії для теплових процесів.
Рівняння (2.9) можна переписати інакше:
|
|
\( Q={{U}_{2}}-{{U}_{1}}+A \) або \( Q=\Delta U+A \), |
(2.9а) |
де \( A=-{A}' \) – робота системи проти зовнішніх сил. Отже,
кількість теплоти, отримана системою, йде на зміну її внутрішньої енергії та на виконання роботи проти зовнішніх сил.
Таке формулювання, звичайно, є рівносильне першому. Але воно є цінне тим, що безпосередньо вказує на можливість виконання механічної роботи за рахунок теплової енергії, тобто перетворення енергії хаотичного руху молекул на енергію впорядкованого руху тіла, приміром, поршня в циліндрі з газом. На цьому ґрунтується робота теплових двигунів (детальніше див. п. 2.4).
При заданій зміні внутрішньої енергії системи співвідношення між отриманою кількістю теплоти та виконаною роботою може бути різним, залежно від процесу, що відбувся. Тож термодинаміка різних процесів, зокрема, розглянутих у п. 1.3, має свою специфіку.
В ізотермічному процесі (T = const), відповідно до формули (2.1), внутрішня енергія не змінюється і рівняння (2.9а) набуває вигляду:
|
|
Q = A. |
(2.10) |
Отже,
в ізотермічному процесі вся отримана системою кількість теплоти йде на виконання механічної роботи.
В ізохорному процесі (V = const) робота A = 0, і
|
|
\( Q=\Delta U \). |
(2.11) |
Отже,
в ізохорному процесі все отримане системою тепло йде тільки на зміну внутрішньої енергії, тобто – зміну температури.
В ізобарному процесі (P = const) отримане тепло йде як на зміну внутрішньої енергії, так і на виконання роботи. Тож із урахуванням формули (2.7), рівняння (2.9a) можна подати як
|
\( Q={{U}_{2}}-{{U}_{1}}+P({{V}_{2}}-{{V}_{1}}) \) або \( Q=\Delta U+P\Delta V \). |
(2.12) |
|
\( Q={{U}_{2}}-{{U}_{1}}+\frac{m}{M}R({{T}_{2}}-{{T}_{1}}) \). |
(2.12a) |
Ще одним із основних термодинамічних процесів є адіабатний процес – процес який здійснюється без теплообміну системи з навколишніми тілами. Іншими словами
адіабатні процеси – це процеси в теплоізольованих системах.
Отже, в адіабатному процесі Q = 0, і для нього рівняння (2.9a) набуває вигляду:
|
або |
\( A={{U}_{1}}-{{U}_{2}}\) \( A=-\Delta U \). |
(2.13) |
Тобто,
в адіабатному процесі механічна робота системи над зовнішніми тілами дорівнює спадові її внутрішньої енергії.
Тож навіть теоретично максимальна робота, що її може виконати система над зовнішніми тілами, не може бути більшою за початковий запас її власної внутрішньої енергії, який завжди є обмеженим. Звідси випливає висновок про навіть теоретичну неможливість "вічного двигуна" – пристрою, що міг би необмежено довго працювати, не отримуючи енергії іззовні. Сьогодні це положення видається самоочевидним, але усвідомлене воно було тільки після встановлення першого закону термодинаміки.
На завершення слід сказати, що теплообмін між тілами неможливо повністю виключити, тож поняття теплоізольованої системи є ідеалізацією. В реальності наближенням до такої системи є термостат (у побуті – якісний термос). Адіабатними також є швидкоплинні процеси в неізольованих системах, коли через короткочасність теплообмін є неістотним.
Рівняння теплового балансу
Дослід свідчить, що в замкнених системах, у яких не виконується механічна робота, процеси завжди йдуть у напрямку встановлення термодинамічної рівноваги, ознакою якої є вирівнювання температур усіх тіл. До прикладу, як це відбувається в калориметрі із уміщеними в нього тілами при різних початкових температурах. При цьому, у відповідності до загального закону збереження енергії, внутрішня енергія системи лишається незмінною:
|
U = \( \sum{{{U}_{i}}}\) = const \( \Rightarrow \) $\sum{\Delta {{U}_{i}}=0}$, |
|
де \( \Delta {{U}_{i}}\) – зміни внутрішньої енергії окремих тіл або частин системи. Без виконання роботи енергії тіл можуть змінюватися тільки шляхом теплообміну. Тож
|
|
ΔUi = Qi, і \( \sum{{{Q}_{i}}}=0 \). |
(2.14) |
Цей вираз називається рівнянням теплового балансу і означає, що
в теплоізольованої системі, в якій не виконується робота, алгебраїчна сума кількостей теплоти, отриманих усіма тілами, дорівнює нулю.
Іншими словами, при встановленні термодинамічної рівноваги без виконання роботи "гарячі" тіла втрачають, а "холодні"– отримують однакову кількість теплової енергії. Тому для практичних розрахунків рівняння теплового балансу зручніше записувати у вигляді:
|
|
\( \sum{{{Q}_{вт}}}=\sum{{{Q}_{от}}} \), |
(2.14а) |
де \( {{Q}_{вт}}\) > 0 і \( {{Q}_{от}}\) > 0 – кількості теплоти, що виділяються гарячими та поглинаються холодними тілами, відповідно.
Для складання рівнянь теплового балансу треба знати формули кількостей теплоти, що характеризують різні термодинамічні процеси і визначаються відповідними питомими теплотами.
При нагріванні чи охолодженні тіла кількість теплоти, якою воно обмінюється з іншими тілами, є прямо пропорційна його масі m та зміні температури:
|
|
Q = cm|(T2 – T1)| = cm|(t2 – t1)|, |
(2.15) |
де величина
$c=\frac{Q}{m\Delta T}$ (Дж/кг·К)
називається питомою теплоємністю і дорівнює кількості теплоти, що є необхідна для зміни температури одиниці маси тіла на одиницю (1К або 10С).
При плавленні кристалічного тіла маси m поглинається, а при твердненні – виділяється кількість теплоти
|
|
\( Q=\lambda m \), |
(2.16) |
де
$\lambda =\frac{Q}{m}$(Дж/кг)
– питома теплота плавлення, рівна кількості теплоти, що є необхідна для перетворення на рідину одиниці маси твердої речовини.
При незмінній температурі перетворення на пару рідини масою m супроводжується поглинанням, а конденсація пари – виділенням кількості теплоти
|
|
\( Q=r{m} \), |
(2.17) |
де
$r=\frac{Q}{m}$(Дж/кг)
– питома теплота пароутворення, рівна кількості теплоти, що поглинається чи виділяється при вказаних перетвореннях одиниці маси речовини.
При згорянні палива масою m, або об'ємом V виділяється кількість теплоти
|
|
\( Q=q{m} \), |
(2.18) |
та
|
|
\( Q=q{V} \), |
(2.19) |
де
$q=\frac{Q}{V}$(Дж/кг та Дж/м3 чи Дж/л)
– питома теплота згоряння (теплотворна здатність, теплотворність), тобто кількість теплоти, що виділяється при згорянні одиниці маси чи об'єму палива.
Усі перераховані питомі величини є табличними характеристиками речовини.
Колові процеси, теплові двигуни
Перший закон термодинаміки вказує на можливість перетворення теплової енергії на механічну. На практиці для цього використовують теплові двигуни, робота яких ґрунтується на колових процесах (циклах).
Коловим процесом (циклом) називається такий, в якому термодинамічна система (на практиці газ) через низку незбіжних станів повертається у вихідний стан. Графік колового процесу зображується замкненою лінією (рис. 2.3) і складається з двох частин: ділянки розширення \( 1\to 2 \) та ділянки стискання \( 2\to 1 \), на якій газ повертається у вихідний стан.

Цикли поділяють на прямі та зворотні. Прямий цикл іде за "годинниковою стрілкою" (суцільні стрілки на графіку), тобто ділянці розширення відповідають більші тиски, ніж ділянці стискання. Зворотній цикл проходить у протилежному напрямку (штрихові стрілки на рис. 2.3).
На кожній ділянці циклу газ виконує роботу: \( {{A}_{1}}>0 \) на ділянці розширення та \( {{A}_{2}}<0 \) на ділянці стискання. Величини A1 і |A2| визначаються площами під відповідними ділянками графіка (див. п. 2.1). Відповідно, повна робота циклу A = A1 + A2 чисельно дорівнює різниці цих площ, тобто, (див. рис. 8.3),
робота газу в циклі чисельно дорівнює площі, обмеженій його графіком на діаграмі (P, V).
При цьому
робота прямого циклу є додатньою, а зворотнього – від'ємною.
Це означає, що зворотній цикл можна здійснити лише "примусово", виконавши над газом відповідну механічну роботу.
За першим законом термодинаміки (п. 2.2) робота газу при переході із стану 1 у стан 2 визначається отриманою ним кількістю теплоти та зміною внутрішньої енергії:
|
|
A12 = Q12 + (U1 – U2). |
|
У кінці циклу U2 = U1, тож повна робота газу в циклі дорівнює повній отриманій ним кількості тепла:
|
A = Q. |
(2.20) |
При цьому реально на різних стадіях циклу газ як отримує (ділянка \( 1\to 2 \)), так і віддає (ділянка \( 2\to 1)\) теплову енергію. Тому отриману величину Q зручно представити як
|
|
Q = Q1 – Q2, |
(2.21) |
де додатні величини Q1 і Q2 – кількості теплоти, що реально отримані та віддані газом на відповідних ділянках прямого циклу. Відповідно, робота циклу
|
A = Q1 – Q2, |
(2.22) |
По завершенню циклу газ повертається у вихідний стан, отож прямий цикл можна повторювати багаторазово, щоразу отримуючи корисну роботу A > 0. На цьому й ґрунтується робота теплових двигунів – пристроїв, які виробляють механічну енергію за рахунок тепла, що виділяється при згорянні палива.
На рис. 2.4 показано термодинамічну схему такого двигуна. Кожний тепловий двигун складається з трьох функціональних елементів: "нагрівника", "робочого тіла" та "холодильника".

Нагрівник являє собою систему з великим запасом внутрішньої енергії, частину якої двигун далі перетворює на механічну роботу.
Робоче тіло – це речовина (газ або пара), в якій здійснюється робочий цикл двигуна, тобто якийсь прямий коловий процес. При цьому робоче тіло спочатку за рахунок частини отриманого тепла Q1 розширюється й виконує додатню роботу, а потім стискається й передає певну кількість теплоти Q2 холодильнику.
Холодильник – це якась система з великою теплоємністю та низькою температурою. Завдяки теплообміну з холодильником робоче тіло повертається у вихідний стан, що дозволяє повторювати цикл знов і знов.
В тепловому двигуні не вся отримана від нагрівника теплова енергія Q1 перетворюється на корисну роботу A. Якась її частина її Q2 обов'язково має віддаватися холодильнику для забезпечення циклічності роботи двигуна. Тож тепловий двигун має певний термодинамічний коефіцієнт корисної дії η (ККД), що дорівнює відношенню роботи А (вирпз (2.21)) до отриманої кількості теплоти Q1:
|
\( \eta=\frac{A}{Q}=\frac{{{Q}_{1}}-{{Q}_{2}}}{{{Q}_{1}}}=1-\frac{{{Q}_{2}}}{{{Q}_{1}}}\). |
(2.23) |
(Через неминучі втрати теплової та механічної енергії у вузлах двигуна реальний ККД є меншим).
Величина (2.23) залежить від виду та параметрів робочого циклу. Максимальний теоретично можливий ККД має так званий "цикл Карно" з ідеальним газом у якості робочого тіла. Відповідний тепловий двигун називається машиною Карно або ідеальним тепловим двигуном. У такому двигуні теплообмін робочого тіла з нагрівником та холодильником здійснюється при сталих температурах Т1 і Т2, і, як показує теорія, ККД визначається формулою:
|
\( \eta_{\text{ід}}=\frac{{{T}_{1}}-{{T}_{2}}}{{{T}_{1}}}=1-\frac{{{T}_{2}}}{{{T}_{1}}}\). |
(2.24) |
В усіх реальних теплових двигунах вихлопні гази (відпрацьоване робоче тіло) в кінці кожного циклу викидаються в атмосферу, отже "холодильником" є навколишнє середовище з температурою T2 порядку 300 K. З іншого боку, температура нагрівника T1 не може бути як завгодно високою через обмежену теплотворність палива та термостійкість технологічних матеріалів, а також погіршення умов функціонування вузлів двигуна при надвисоких температурах. Тому реальний ККД навіть найкращих теплових двигунів складає порядку 50% .
Теплова енергія, що викидається в атмосферу (тобто віддається холодильнику), незворотньо втрачається і вже не може бути перетворена на корисну роботу. Отже, при роботі теплових двигунів відбувається знецінення теплоти як можливого джерела механічної енергії. Це, як доведено, стосується будь-яких реальних теплових процесів і є проявом універсального закону природи – другого начала термодинаміки. Але його детальний розгляд виходить за рамки елементарної фізики.
2.2. Приклади розв’язування задач
Застосування основних законів термодинаміки для розв'язування задач ілюструють наведені приклади, котрі згруповано за наступними темами:
I закон термодинаміки та термодинаміка ізопроцесів у газах
Колові процеси, теплові двигуни
У текстах пропонованих задач і відповідях прийнято ті самі умови по умовчанню, що і в попередньому розділі.
Перший закон термодинаміки та термодинаміка ізопроцесів у газах
Задача 2.1. При швидкому стисканні m = 4 г гелію (М = 4 г/моль) в циліндрі під поршнем газ нагрівається від t1 = 7°C до t2 = 87°C. Визначити роботу A стискання газу.
Задача 2.2. При переміщенні поршня парової машини на відстань l = 60 см тиск пари в циліндрі лінійно спадає від P1 = 1,0 МПа до P2 = 0,2 МПа, а температура понижується до t2 = 107°C. Початковий об'єм пари V1 = 10 л, площа поршня S = 1000 см2. Визначити: А) роботу пари A і Б) її початкову температуру t1.
Задача 2.3. Температуру одного моля газу в циліндрі під поршнем змінюють від t1 = 10°C до t2 = 75°C. Визначити: А) кількість теплоти, отриманої газом при закріпленому (QV) та вивільненому (QP) поршні; Б) роботу газу А.
Задача 2.4. Незмінну кількість газу переводять із стану 1 у стан 2 двома заданими способами ("шляхами"): а) 1-1'-2 та б) 1-2 (див. розв'язання, рис. 4). Визначити відношення кількостей тепла (Q1/Q2), отриманих газом у кожному випадку, якщо відношення кінцевого та початкового тисків (Р2/Р1) складає n = 9.
Задача 2.5. Газ у кількості ν = 0,2 моль із початковими об'ємом V1 = 5 л і тиском Р1 = 100 кПа нагрівають у циліндрі з рухомим поршнем так, що тиск весь час є прямо пропорційний до об'єму P ~ V. Визначити: 1. Зв'язок між температурою та тиском газу в такому гіпотетичному процесі; 2. Роботу газу при збільшенні його об'єму в n = 2 рази.
Задача 2.6. Два молі газу в циліндрі під поршнем спочатку ізобарно розширюють у n = 2 рази, а потім ізохорно охолоджують до вихідної температури. Визначити максимальну температуру газу, якщо різниця отриманої та відданої ним в процесі кількості теплоти ΔQ = 8,3 кДж. Газова стала R = 8,3 Дж/(моль·K).
Задача 2.1
При швидкому стисканні m = 4 г гелію (М = 4 г/моль) в циліндрі під поршнем газ нагрівається від t1 = 7 °C до t2 = 87 °C.
Визначити
·роботу A стискання газу.
|
Дано: m = 4·10–3 кг
М = 4 кг/кмоль
t1 = 280 К
t2 = 360 К
|
|
A - ? |
Розв’язання
Через швидкоплинність процесу теплообміном газу із навколишніми тілами можна знехтувати й уважати процес адіабатним (див. п. 2.2). Отже, робота стискання А йде тільки на зміну внутрішньої енергії U, котра визначається формулою (2.1):
\(A=\frac{3}{2}\cdot \frac{mR}{M}({{T}_{2}}-{{T}_{1}})\).
Обчислення дають
А ≈ 1,0 кДж.
Задача 2.2
При переміщенні поршня парової машини на відстань l = 60 см тиск пари в циліндрі лінійно спадає від P1 = 1,0 МПа до P2 = 0,2 МПа, а температура понижується до t2 = 107°C. Початковий об'єм пари V1 = 10 л, площа поршня S = 1000 см2.
Визначити:
А) роботу A і
Б) початкову температуру пари t1.
|
Дано: l = 0,6 м
P1 = 106 Па
P2 = 2·105 Па
T2 = 380 К
V1 = 10–2 м3
S = 0,1 м2
|
|
A - ? t1 - ? |
Розв’язання
А). Роботу пари визначимо за графіком процесу (див. п. 2.1) через  площу виділеної трапеції на рис. 2:
площу виділеної трапеції на рис. 2:
\(A=\frac{1}{2}({{P}_{1}}+{{P}_{2}})({{V}_{2}}-{{V}_{1}})\),
де зміна об’єму пари V2 – V1 = lS. Отже,
\(A=\frac{({{P}_{1}}+{{P}_{2}})LS}{2}=3,6\cdot {{10}^{4}}\) Дж = 36 кДж.
Б). Згідно з рівнянням Клапейрона (1.13),
\(\begin{align} & {{P}_{1}}{{V}_{1}}=\nu R{{T}_{1}}, \\ & {{P}_{2}}{{V}_{2}}=\nu R{{T}_{2}}. \\ \end{align}\)
Тож
\(\frac{{{T}_{1}}}{{{T}_{2}}}=\frac{{{P}_{1}}{{V}_{1}}}{{{P}_{2}}{{V}_{2}}}.\)
Звідси, врахувавши, що V2 = V1 + lS, одержимо наступну відповідь:
\({{T}_{1}}={{T}_{2}}\cdot \frac{{{P}_{1}}{{V}_{1}}}{{{P}_{2}}({{V}_{1}}+lS)}=\frac{({{{P}_{1}}}/{{{P}_{2}}}\;)}{1+{lS}/{{{V}_{1}}}\;}\cdot {{T}_{2}} \) K.
Обчислення дають
T1 = 475 K → t1 = 2о2°С.
Задача 2.3. Температуру одного моля газу в циліндрі під поршнем змінюють від t1 = 10°C до t2 = 75°C.
Визначити
А) кількість теплоти, отриманої газом при закріпленому QV) та вивільненому (QP) поршні;
Б) роботу газу А.
|
Дано: ν = 1 моль
t1 = 10°C
t2 = 75°C
|
|
QV - ?; QP - ? |
Розв’язання
A) При закріпленому поршні об'єм газу V = const, тобто нагрівання є ізохорним. Тож відповідно до формули (2.11)
QV = ΔU,
де ΔU – зміна внутрішньої енергії, котра визначається формулою (2.3):
\(\Delta U=\frac{3}{2}\nu R({{T}_{2}}-{{T}_{1}})\).
Таким чином, при закріпленому поршні газ одержує кількість тепла
QV = $\frac{3}{2}\nu R\left( {{T}_{2}}-{{T}_{1}} \right)$ = 809 Дж.
Б) За відсутності тертя в будь-якому положенні поршня тиск газу в циліндрі дорівнює зовнішньому тиску, тож нагрівання газу є ізобарним (P = const). При цьому, відповідно до формул (2.8) і (2.12а) отримана ним кількість тепла QP дорівнює:
QP = $\frac{3}{2}\nu R\left( {{T}_{2}}-{{T}_{1}} \right)$ +$\frac\nu R\left( {{T}_{2}}-{{T}_{1}} \right)$ \(\Rightarrow\) QP = \(\frac{5}{2}\nu R({{T}_{2}}-{{T}_{1}})\) = 1,35 кДж.
Таким чином, для однакової зміни температури газу при вільному поршні необхідно витратити більшу кількість теплоти, ніж при закріпленому. Це й зрозуміло, бо якщо при незмінному об'ємі на нагрівання йде все отримане тепло, то при постійному тиску – тільки його частина, а решта витрачається на виконання газом роботи розширення A. Тож при однаковій зміні температури (і, відповідно, внутрішньої енергії)
QP – QV = A.
Задача 2.4. Незмінну кількість газу переводять із стану 1 у стан 2 двома заданими способами  ("шляхами") а) 1-1'-2 та б) 1-2, рис. 4 .
("шляхами") а) 1-1'-2 та б) 1-2, рис. 4 .
Визначити
відношення кількостей тепла (Qa/Qb), отриманих газом у кожному випадку, якщо відношення кінцевого та початкового тисків (Р2/Р1) складає n = 9.
|
Дано: (P2/P1) = n
n = 9
|
|
(Qa/Qb) - ? |
Розв’язання
За першим законом термодинаміки (2.9а) отримана газом кількість тепла в кожному випадку визначається зміною його внутрішньої енергії та виконаною роботою:
|
Q = ΔU +A. |
(1) |
Як видно з рис. 4, при обох зазначених в умові способах зміни стану газу відношення крайніх значень об'ємів і тисків однакові:
$\frac{{{V}_{2}}}{{{V}_{1}}}=\frac{{{P}_{2}}}{{{P}_{1}}}=n$.
Однаковими є й зміни внутрішньої енергії газу, котрі, згідно з формулою (2.2) і вказаним зв'язком між крайніми параметрами, дорівнюють:
|
$\Delta U=\frac{3}{2}\left( {{P}_{2}}{{V}_{2}}-{{P}_{1}}{{V}_{1}} \right)=\frac{3}{2}\left( {{n}^{2}}-1 \right){{P}_{1}}{{V}_{1}}$ |
(2) |
Роботу газу у випадку a) і b) визначимо як виділену площу на рис. 4-1а та 4-1б:
і b) визначимо як виділену площу на рис. 4-1а та 4-1б:
Aa = P2(V2 – V1) \(\Rightarrow\) Aa = n(n–1)P1V1,
\({{A}_{b}}=\frac{1}{2}({{P}_{1}}+{{P}_{2}})({{V}_{2}}-{{V}_{1}})\) \(\Rightarrow\) \({{A}_{b}}=\frac{({{n}^{2}}-1){{P}_{1}}{{V}_{1}}}{2}.\)
Відтак підставимо ці вирази в рівняння (1) і, врахувавши вираз (2), після перетворень знайдемо
\({{Q}_{a}}=\frac{(n-1)(5n+3)}{2}{{P}_{1}}{{V}_{1}};\)
Qb = 2(n2 – 1)P1V1.
\(\frac{{{Q}_{1}}}{{{Q}_{2}}}=\frac{5n+3}{4(n+1)}=1,2.\)
Задача 2.5. Газ у кількості ν = 0,2 моль із початковими об'ємом V1 = 5 л і тиском Р1 = 100 кПа нагрівають у циліндрі з рухомим поршнем так, що тиск весь час є прямо пропорційний до об'єму: P ~ V.
Визначити:
1. Зв'язок між температурою та тиском газу в такому гіпотетичному процесі;
2. Роботу газу при збільшенні його об'єму в n = 2 рази.
|
Дано: ν = 0,2 моль
Р1 = 105 Па
V1 = 5·10–3 м3
n = 2
|
|
Т(V) - ?, А - ? |

Розв'язання
Умову задачі наочно відображає графік процесу, рис. 5.
1. Згідно з рівнянням Клапейрона (7.13) температура заданої кількості газу визначається добутком тиску цй об'єму:
$T=\frac{PV}{\nu R}$
Отже, аби встановити залежність Т(P), треба знати зв'язок між об'ємом і тиском газу, який в даній задачі, згідно з рис. 5, має вигляд:
$\frac{P}{V}=\frac{{{P}_{1}}}{{{V}_{1}}}\quad \Rightarrow \quad V=\frac{{{V}_{1}}}{{{P}_{1}}}P$,
Відтак, урахувавши це співвідношення у виразі (1), отримаємо:
$T=\alpha {{P}^{2}}$
де
$\alpha =\frac{{{V}_{1}}}{\nu R{{P}_{1}}}$ = 3·10–8 (К/Па2)
2. Роботу газу визначимо за площею під виділеною на рис. 2.5 ділянкою графіка процесу (див. п.2.1):
\(A=\frac{1}{2}\left( P_2+P_{1} \right)\left( V_2-V_0\right)\),
і, враховуючи задане співвідношення n між крайніми значеннями параметрів, дістанемо:
$A=\frac{{{n}^{2}}-1}{2}{{P}_{1}}{{V}_{1}}$ = 750 Дж.
Задача 2.6. Два молі газу в циліндрі під поршнем спочатку ізобарно розширюють в n = 2 рази, а потім ізохорно охолоджують до вихідної температури.
максимальну температуру газу Т, якщо різниця отриманої та відданої ним кількості теплоти ΔQ = 8,3 кДж. Газова стала R = 8,3 Дж/(моль·K).
|
Дано: ν = 2 моль
n = 2
ΔQ = 8,3·103 Дж
|
|
Т - ? |
Розв'язання
Шукана максимальна температура газу відповідає точці 1′(P1,V2) на графіку заданого комбінованого процесу (рис. 6).
Згідно з першим законом термодинаміки, отримане Q1 чи віддане Q2 газом тепло, на загал визначається зміною його внутрішньої енергії та виконаною роботою:
Q = ΔU + A.
Але, позаяк за умовою кінцева й початкова температури є однакові, приріст внутрішньої енергії газу при нагріванні дорівнює її спадові при охолодженні. Тому різниця отриманої та відданої кількостей теплоти ΔQ дорівнює тільки роботі газу при ізобарному розширенні й визначається формулою (2.7). Отже,
|
ΔQ = P1(V2 – V1). |
(1) |
Так само через рівність початкової та кінцевої температур, точки 1 і 2 належать одній ізотермі, отже,
|
${{P}_{1}}{{V}_{1}}={{P}_{2}}{{V}_{2}}\quad \Rightarrow \quad {{V}_{1}}=\frac{{{P}_{2}}}{{{P}_{1}}}{{V}_{2}}=\frac{1}{n}{{V}_{2}}$. |
|
Зробивши таку заміну у виразі (1), дістанемо
|
$\Delta Q=\frac{n-1}{n}{{P}_{1}}{{V}_{2}}=\frac{n-1}{n}\nu RT$, |
(2) |
і відтак отримаємо наступну відповідь:
$T=\frac{n\Delta Q}{\left( n-1 \right)\nu R}=1000\text{ K}$.
Рівняння теплового балансу
У наведених прикладах задач, у яких фігурує прискорення вільного падіння, його значення приймається рівним g = 10 м/с2.
Задача 2.7. Для ванни необхідно приготувати V = 200 л води з температурою t = 46°C, змішуючи гарячу та холодну воду з температурами \(t_{1}\) = 90°C і \(t_{2}\) = 10°C. Визначити потрібні об'єми гарячої V1 та холодної V2 води.
Задача 2.8. Кусок припою (сплав олова зі свинцем) з температурою \({{t}_{1}}\) = 100°C опустили в калориметр із такою самою масою води при температурі \({{t}_{2}}\) =10°C. Визначити вміст олова ηo(%) і свинцю ηc(%) у припої, якщо в калориметрі встановилася температура \(t\) = 13,5 °C.
Задача 2.9. У термос із m = 2 кг льоду (питома теплота плавлення λ = 330 кДж/кг) при температурі t0 = 0°C влили V = 1,5 л окропу (густина ρ = 1 г/см3, питома теплоємність c = 4,2 кДж/(кг·К)) з температурою t = 95°C. Визначити температуру $\theta $, що встановиться у термосі.
Задача 2.10. У плавильній печі з коефіцієнтом корисної дії \(\eta\) = 40 % треба розплавити m = 50 т залізного брухту із початковою температурою t = 25°C. Визначити потрібну для цього масу коксу m1.
Задача 2.11. При інтенсивному відкачуванні теплоізольованої колби з водою при температурі 0°С і нормальному атмосферному тиску утворилася певна кількість льоду. Визначити, яка частина η(%) води при цьому випарувалася. Питома теплота плавлення льоду λ = 335 кДж/кг, питома теплота пароутворення r = 2,26 МДж/кг.
Задача 2.7
Для ванни необхідно приготувати V = 200 л води з температурою t = 46°C, змішуючи гарячу та холодну воду з температурами \(t_{1}\) = 90°C і \(t_{2}\) = 10 °C.
Визначити
потрібні об'єми гарячої V1 та холодної V2 води.
|
Дано: V = 200 л
t = 46 °C
\(t_{1}\) = 90 °C
\(t_{2}\) = 10 °C
|
|
V1, V2 - ? |
Розв’язання
У процесі встановлення теплової рівноваги при змішуванні гаряча та холодна вода обмінюються однаковими кількостями теплоти, тож відповідно до формули (2.15) маємо:
cm1(t1 – t) = cm2(t – t2).
Виразивши маси гарячої m1 і холодної m2 води через густину та об'єми, отримаємо
V1(t1 – t) = V2(t – t2)
і, врахувавши, що V = V1 + V2, легко дістанемо відповідь:
\(V_{1}=\frac{t-t_{2}}{t_{1}-t_{2}}{V}=90\) л
\(V_{2}=V-V_{1}=\frac{t_{1}-t}{t_{1}-t_{2}}{V}=110\) л.
Задача 2.8
Кусок припою (сплав олова зі свинцем) з температурою \({{t}_{1}}\) = 100°C опустили в калориметр із такою самою масою води при температурі \({{t}_{2}}\) =10°C. Питомі теплоємності: води c = 4,2 кДж/(кг·К), олова co = 230 Дж/(кг·К), свинцю cс = 130 Дж/(кг·К).
Визначити
вміст олова ηo(%) і свинцю ηc(%) у припої, якщо в калориметрі встановилася температура \(t\) = 13,5 °C.
|
Дано: t1 = 100°C
t2 =10°C
t = 13,5°C
co = 230 Дж/(кг·К)
cс = 130 Дж/(кг·К)
c = 4,2 кДж/(кг·К)
|
|
ηо (%) - ? ηс (%) - ?
|
Розв’язання
У процесі встановлення теплової рівноваги олово і свинець охолоджуються, а вода нагрівається до заданої кінцевої температури t. Тож відповідно до рівняння теплового балансу (2.14a) і формули (2.15), можна записати:
|
como(t1 – t) + ccmc(t1 – t) = cm(t – t2), |
(1) |
де m – маса води в калориметрі, а mо і mc – маси олова і свинцю в сплаві.
Вміст компоненти η є відношенням її маси до загальної маси сплаву, тож, урахувавши, що за умовою маса припою збігається з масою води, маємо:
|
mо = ηоm, mс = ηсm і ηо + ηс= 1 $\Rightarrow $ ηс = 1– ηо . |
|
Відтак, підставивши ці вирази в рівняння (1), отримаємо рівняння
\(\left( {{c}_{\text{o}}}{{\eta }_{\text{o}}}+{{c}_{\text{c}}}\left( 1-\eta_{\text{o}} \right) \right)\left( {{t}_{1}}-t \right)={{c}_{\text{в}}}\left( t-{{t}_{2}} \right)\)
з якого дістанемо величину ηо, а по тому й ηс:
${{\eta }_{\text{o}}}=\frac{{{c}_{\text{}}}\left( t-{{t}_{2}} \right)}{\left( {{c}_{\text{o}}}-{{c}_{\text{c}}} \right)\left( {{t}_{1}}-t \right)}-\frac{{{c}_{\text{c}}}}{{{c}_{\text{o}}}-{{c}_{\text{c}}}}$; ηс = (1 – ηо).
Обчислення дають
ηо = 40%; ηс = 60%.
Задача 2.9
У термос із m = 2 кг льоду (питома теплота плавлення λ = 330 кДж/кг) при температурі t0 = 0°C влили V = 1,5 л окропу (густина ρ = 1 г/см3, питома теплоємність c = 4,2 кДж/(кг·К)) з температурою t1 = 95°C.
Визначити
температуру θ, що встановиться у термосі.
|
Дано: m = 2 кг
V = 1,5 л
t0 = 0°C
t = 95°C
λ = 330 кДж/кг
ρ = 1 г/см3
|
|
θ -? |
Розв’язання
Шукана температура θ знаходиться з рівняння теплового балансу (2.14а), в якому віддане тепло за формулою (2.15) складає
${{Q}_{в}}=c\rho V\left( t-\theta \right)$,
де ρV – маса влитого окропу, а отримане
${{Q}_{о}}=\lambda m+cm\left( \theta -{{t}_{0}} \right)$,
де m – маса розплавленого льоду та утвореної з нього води.
Отже, для визначення кінцевої температури в термосі маємо рівняння:
|
|
$c\rho V\left( t-\theta \right) =\lambda m+cm\left( \theta -{{t}_{0}} \right)$. |
(1) |
При цьому, коли підставити нього задану в умові величину m = 2 кг, то обчислення дають θ = –51°C, тобто виходить, що при заливанні окропу лід у термосі не тане, а глибоко заморожується, що є абсурдом. Але його причину неважко збагнути: залитого окропу є замало для розплавлення всього льоду. І справді, за формулою (2.16) для розплавлення 2 кг льоду потрібно 660 кДж тепла, тоді як за формулою (2.15) окріп масою ρV = 1,5 кг при охолодженні до θ = 0°C віддає вього ≈ 600 кДж. Тож розплавляється тільки частина льоду, масу котрої m′ можна визначити, поклавши в рівнянні (1) θ = 0:
$m′ =\frac{cm{{t}}}{\lambda }$ = 1,8 кг.
Отже, маємо таку відповідь задачі:
після встановлення рівноваги термос буде містити воду з кусочком льоду масою 200 г при температурі
θ = 0°C.
Порада. Аби за наявності в системі фазових переходів (змін агрегатного стану) при складанні рівняння теплового балансу запобігти подібній до зробленої тут умисно помилки, варто попередньо підрахувати та з'ясувати сумісність із умовою задачі кількостей теплоти, що потрібні для повної зміни агрегатного стану відповідних речовин.
Задача 2.10
У плавильній печі з коефіцієнтом корисної дії η = 40 % необхідно розплавити m = 50 т залізного брухту, що має початкову температуру t = 25°C. Температура плавлення заліза tп = 1425°C, питома теплоємність c = 460 Дж/(кг·К), питома теплота плавлення λ = 82 кДж/кг. Теплотворність коксу q = 35 МДж/кг.
Визначити
потрібну для цього масу коксу m1.
|
Дано: η = 40 %
m = 50 т
t = 25 °C
tп = 1425 °C
c = 460 Дж/(кг·К)
λ = 82 кДж/кг
q = 35 МДж/кг
|
|
m1 - ?
|
Розв’язання
Згідно з формулою (2.18), потрібна маса кокусу m1 визначається його теплотворністю q та кількістю теплоти Q1, що є необхідна для нагрівання й плавлення брухту:
|
|
${{m}_{1}}=\frac{{{Q}_{1}}}{q}$. |
|
При цьому корисною (що йде безпосередньо на нагрівання та плавлення) є тільки частка Q = ηQ1 всієї виділеної при згорянні коксу кількості теплоти. Тож
|
${{m}_{1}}=\frac{Q}{\eta q}$, |
(1) |
де величина Q визначається формулами (2.15) і (2.16). Таким чином,
\({{m}_{1}}=\frac{(c({{t}_{}}-t)+\lambda )m}{\text{ }\!\!\eta\!\!\text{ }q}\) ≈ 2,6 т.
Задача 2.11. При інтенсивному відкачуванні теплоізольованої колби з водою при температурі 0°С і нормальному атмосферному тиску утворилася певна кількість льоду.
Визначити,
яка частина η(%) води при цьому випарувалася. Питома теплота плавлення льоду λ = 335 кДж/кг, питома теплота пароутворення r = 2, 26 МДж/кг.
|
Дано: λ = 335 кДж/кг
r = 2,26 МДж/кг
|
|
η - ?
|
Розв’язання
При пароутворенні рідину покидають "гарячі" молекули, енергія теплового руху котрих є достатня для подолати сил зв'язку з іншими молекулами. Через це рідина охолоджується і при інтенсивному випаровуванні без підведення тепла іззовні може навіть тверднути.
За умовою вода в колбі із самого початку перебуває при температурі тверднення. Тому при відкачуванні колби вода відразу починає замерзати, тож усе тепло, що при цьому виділяється, йде на пароутворення. Отже, згідно з формулами (2.16) і (2.17),
rmп = λmл,
де mп – маса води, що випарувалась, і mл = m – mп– маса утвореного льоду при початковій масі води в колбі m. Тобто,
\(\lambda \left( m-{{m}_{\text{п}}} \right)=r{{m}_{\text{п}}}\quad \Rightarrow \quad \lambda m=\left( \lambda +r \right){{m}_{\text{}}}\).
Отже, частка η = (mп/m) води, що перетворилася на пару, складає:
$\eta =\frac{λ}{r+\lambda }$ = 13%.
Колові процеси. Теплові двигуни
Роботу колового процесу (циклу) зручно визначати через площу його графіка, зобразивши його при потребі на діаграмі (P,V).
Задача 2.12. Із незмінною кількістю ідеального газу проведено заданий коловий процес (рис. 12. у розв'язанні). Побудувати графіки залежності тиску від 1) температури P(T) та 2) об'єму P(V) у цьому процесі.
Задача 2.13. З незмінною кількістю одноатомного газу проводять заданий прямий цикл (див. рис. у розв'язанні), в якому максимальний і мінімальний тиски співвідносяться як P2 = nP1, n = 8. Визначити коефіцієнт корисної дії циклу \(\eta\).
Задача 2.14. Парова машина потужністю N = 12 кВт витрачає за час τ = 1 год m = 8 кг палива з теплотворністю q = 36 МДж/кг. Пара подається в циліндр машини при температурі t1 = 200 °C, а викидається в конденсатор (холодильник) при температурі t2 = 100 °C. Визначити ККД η машини та порівняти його з ККД ηк ідеального теплового двигуна (машини Карно), що працює при тих самих температурах нагрівника та холодильника.
Задача 2.15. ККД ідеального теплового двигуна η теоретично можна збільшити або підвищенням температури нагрівача, або зниженням температури холодильника. Визначити, в якому випадку й на скільки ε(%) приріст ККД буде більшим?
 Із незмінною кількістю ідеального газу проведено заданий коловий процес (цикл), показаний на рис. 12.
Із незмінною кількістю ідеального газу проведено заданий коловий процес (цикл), показаний на рис. 12.
Побудувати
графіки залежності тиску від 1) температури P(T) та 2) об'єму P(V) у цьому циклі.
Розв’язання
Із заданого графіка циклу видно, що він складається з ізохор (1→2), (3→4), ізотерми 2→3, та ізобари 4→1.

1). Залежність Р(T). Задля зручності побудови графіка розміщуємо систему координат (Р,Т), як показано на рис. 12-1, і з точок 1, 2, 3 і 4 на рис. 12а) опускаємо проєктуючі вертикалі на рис. 12б) та вибираємо на ньому початкову точку 1. Відтак з початку координат проводимо промінь через т.1 до перетину з вертикаллю Т23 і стрілк0ю зображуємо початкову ділянку циклу 1→2. (Примітка. Позаяк числові дані, зокрема Р1, в умові не вказані, положення т.1 вибираємо довільно, проте так, аби т.2 не виходила за межі креслення).
Далі, враховуючи, що на ділянці 4→1 процес є ізобарним, проводимо горизонталь через т.1 і на її перетині з вертикаллю Т4 відмічаємо точку 4. Після цього, врахувавши, що ділянка 3→4 є ізохорою, проводимо промінь із початку координат через т.4 до перетину з вертикаллю Т2,3 і знаходимо положення т.3. Відтак, спорядивши стрілками ділянки 2→3→4→1, завершуємо побудову графіка залежності Р(T).
2. Залежність Р(V) на графіку будуємо за такою самою схемою шляхом "проєктування" щойно отриманого графіка Р(Т). Для цього координатну систему (Р,V) розміщуємо праворуч (рис. в)) й переносимо на вісь абсцис значення V12 і V34 з рис. а). По тому проводимо з цих точок проєктуючі вертикалі, а з точок Р14, Р3 і Р2 – горизонталі. Відтак на перетинах проєктуючих відмічаємо відповідні точки й показуємо графік циклу, як на рис. в).
З незмінною кількістю одноатомного газу проводять прямий цикл заданий прямий цикл (рис. 13), у якому максимальний і мінімальний тиски співвідносяться як P2 = nP1, n = 8.
Визначити
коефіцієнт корисної дії циклу \(\eta\).
|
Дано: P2 = nP1
n = 8
|
|
\(\eta\) - ?
|
Розв’язання

Відповідно до рис. 13, заданий цикл складається з ізохори \(1\to {1}'\), ізобари \({1}'\to 2\) і ділянки \(2\to {1}\), на якій тиск і об'єм перебувають у прямо пропорціональному зв'язку.
Коефіцієнт корисної дії циклу визначається як
|
\(\eta=\frac{{{A}}}{{{Q}_{1}}},\) |
(1) |
де A – робота газу в циклі, Q1, – кількість тепла, отримана ним на гілці 1 → 1′ → 2.
Величина A чисельно дорівнює площі виділеного трикутника на рис. 13 (див. п. 2.1) і складає
|
$A=\frac{1}{2}\Delta P\Delta V=\frac{1}{2}{{\left( n-1 \right)}^{2}}{{P}_{1}}{{V}_{1}}$ |
(2) |
Теплота Q1 за першим законом термодинаміки йде на зміну внутрішньої енергії газу, що згідно з виразом (2.4), складає
|
$\Delta U=\frac{3}{2}\Delta \left( PV \right)=\frac{3}{2}{{\left( n-1 \right)}^{2}}{{P}_{1}}{{V}_{1}}$, |
(3) |
та на роботу розширення газу на ділянці 1′ → 2, яка відповідно до формули (2.7) дорівнює
|
${{A}_{1}}=n\left( n-1 \right){{P}_{1}}{{V}_{1}}$. |
(4) |
Тож підставивши ці значення у вираз (2.9a), після викладок дістанемо:
${{Q}_{1}}=\frac{1}{2}\left( 5{{n}^{2}}-2n-3 \right){{P}_{1}}{{V}_{1}}$.
Відтак за формулою (1) отримаємо відповідь:
|
$\eta =\frac{{{\left( n-1 \right)}^{2}}}{5{{n}^{2}}-2n-3}=16,3$%. |
|
Парова машина потужністю N = 12 кВт витрачає за час τ = 1 год m = 8 кг палива з теплотворністю q = 36 МДж/кг. Пара подається в циліндр машини при температурі t1 = 200 °C, а викидається в конденсатор (холодильник) при температурі t2 = 100 °C.
Визначити
ККД η машини та порівняти його з ККД ηк ідеального теплового двигуна (машини Карно), що працює при тих самих температурах нагрівника та холодильника.
|
Дано: N = 12 кВт
τ = 1 год
m = 8 кг
q = 36 МДж/кг
t1 = 200°С
t2 = 10°C
|
|
\(\eta\) - ?
\(\eta_{ід}\) - ?
|
Розв’язання
Коефіцієнт корисної дії теплової машини (двигуна)
\( \eta=\frac{A}{Q}\),
де A – виконана робота, Q – отримана кількість тепла. З умови задачі зрозуміло, що
\( {A}=N\tau \) і \( {Q}=qm, \)
отже
\( \eta=\frac{N\tau }{qm}=0,15=15 \) %.
ККД машини Карно (ідеального теплового двигуна) при вказаних температурі нагрівника та холодильника за формулою (2.24) складає:
\( \eta_{ід}=1-\frac{{{T}_{2}}}{{{T}_{1}}}=21 \) %.
Отже, ККД даного теплового двигуна є менший, ніж ККД відповідного ідеального двигуна, як про те й трактує теорія.
Задача 2.15. ККД ідеального теплового двигуна η теоретично можна збільшити або підвищенням температури нагрівача, або зниженням температури холодильника.
Визначити,
в якому випадку й на скільки ε(%) приріст ККД буде більшим?
Розв’язання
Згідно з теорією (п. 2.4), ККД ідеального теплового двигуна визначається формулою (2.24). Тож при підвищенні температури нагрівника на якусь величину ΔТ він набуде значення
${{\eta }_{1}}=\frac{\left( {{T}_{1}}+\Delta T \right)-{{T}_{2}}}{{{T}_{1}}+\Delta T}$.
Якщо ж замість цього на таку саму величину понизити температуру холодильника, то ККД стане рівним
${{\eta }_{2}}=\frac{{{T}_{1}}-\left( {{T}_{2}}-\Delta T \right)}{{{T}_{1}}}$.
Як видно, в отриманих виразах чисельники однакові, отже для підвищення ККД є більш ефективно зменшувати температуру холодильника. На скільки саме, показує величина
$\varepsilon =\frac{{{\eta }_{2}}-{{\eta }_{1}}}{{{\eta }_{1}}}=\frac{{{\eta }_{2}}}{{{\eta }_{1}}}-1$,
для якої після підстановки виразів η1 і η2 дістанемо:
$\varepsilon =\frac{\Delta T}{{{T}_{1}}}$.
Слід сказати, що отриманий результат практичного значення не має, бо всі реальні теплові двигуни (приміром, автомобільні) за холодильник мають довкілля. Причина цього полягає в тому, що як доводить теорія, затрачена на примусове охолодження холодильника енергія принципово не може бути меншою за отриманий через підвищення ККД виграш.
2.3. Задачі для самостійної роботи
У пропонованих задачах по умовчанню гази вважаються ідеальними, тертя в циліндрах із поршнями відсутнім, а самі поршні – невагомими (якщо не сказано про інше). У відповідях прийнято g = 10 м/с2, а також, що внутрішня енергія газу визначається формулами (2.1) і (2.2) незалежно від кількості атомів у молекулі.
Для аналізу внутрішньої енергії та роботи газу в заданому процесі корисно зобразити його на графіку в координатах (P,V) і при складанні робочих рівнянь правильно враховувати знаки величин Q, ΔU, A, беручи до уваги, що в комбінованому процесі кінцеві значення внутрішньої енергії та параметрів стану на даній ділянці процесу є початковими для наступної.
Додамо також, що при обчисленнях температуру в °С обов’язково слід переводити в кельвіни (К).
Рекомендовані задачі згруповано по темах:
Перший закон термодинаміки
Рівняння теплового балансу
Колові процеси. Теплові двигуни
Перший закон термодинаміки
Рівень А
| 2.16. |
Газ у циліндрі з тиском 100 кПа й об'ємом 6 л адіабатно стискають так, що тиск змінюється в 10 разів, а об'єм – у 4 рази. Визначити роботу газу в процесі [–540 Дж] |
|
| 2.17. |
Гелій масою 100 г в циліндрі під поршнем при адіабатному розширенні виконав роботу 25 кДж. Визначити зміну температури газу. [–12°С] |
|
| 2.18. |
Чому дорівнює теплоємність газу в ізотермічному та в адіабатному процесі? [∞; 0] |
|
| 2.19. |
Визначити середню кінетичну енергію молекули газу, один моль якого при тиску 100 кПа займає об'єм 6 л. [1,5·10–21 Дж] |
|
| 2.20. |
Визначити роботу 320 г кисню при нагріванні на 10°С у циліндрі під рухомим поршнем. [830 Дж] |
|
| 2.21. |
Визначити, на скільки відрізняються кількості теплоти, потрібні для нагрівання 5 моль повітря на 10°С один раз при сталому тиску, а інший – при сталому об'ємі? [415 Дж] |
|
| 2.22. |
Визначити зміну температури одного моля повітря в циліндрі під рухомим поршнем, якщо воно виконало роботу 300 Дж. [36°С] |
|
| 2.23. |
Визначити зміну температури 2 кг гелію в адіабатному процесі, якщо газ виконав роботу 125 кДж. [–20°С] |
|
| 2.24. |
Визначити роботу газу при адіабатному розширенні від об'єму 20 дм3 до 0,1 м3, якщо його початковий тиск складав 200 кПа, а кінцевий – 13,7 кПа? [3,95 кДж] |
|
|
|
Рівень Б
| 2.25. |
У циліндрі під рухомим поршнем міститься 300 г газу, густина котрого за нормальних умов (760 мм.рт.ст., 0°С) складає 1,3 кг/м3. Визначити роботу газу при його нагріванні на 100°С. [8,6 кДж] |
|
| 2.26. |
Визначити кількість теплоти, яку треба передати одному молю газу для його нагрівання на 10°С у процесі, в якому тиск і об'єм перебувають у прямопропорційній залежності. [166 Дж] |
|
| 2.27. |
Кисень масою 300 г із початковою температурою 47°С ізохорно охолоджують так, що тиск зменшується втричі. Відтак газ нагрівають ізобарно до початкової температури. Визначити кількість теплоти, що передано газу. [16,6 кДж] |
|
| 2.28. |
Знайти початкову температуру двох молів газу, якщо при ізобарному подвоєнні об'єму й наступному ізохорному охолодженні до вихідної температури газ виконав роботу 4,15 кДж. [–23°С] |
|
| 2.29. |
Ідеальний газ розширяються так, що його тиск лінійно зростає від 400 кПа до 800 кПа при збільшенні об'єму від 0,2 м3 до 0,5 м3. Знайти: а) роботу газу; б) зміну його внутрішньої енергії; в) отриману кількість теплоти. [а) 180 кДж; б) 480 кДж; в) 660 кДж] |
|
| 2.30. |
При зміні об'єму азоту масою 7 г від 1 м3 до 2 м3 його температура змінювалася за законом T = αV2, де α = 2 К/м6. Знайти роботу, яку виконав газ. Отримував, чи втрачав газ при цьому тепло? [6,2 Дж; отримував] |
|
| 2.31. |
При розширенні газу його тиск зменшується за законом P = P0 – αV, де α = 0,2 МПа/м3. Яку кількість теплоти одержує газ при зміні об'єму від 1 м3 до 2 м3 ? [50 кДж] |
Рівняння теплового балансу
При складанні рівняння теплового балансу, якщо напрям теплообміну (знак зміни температури) для всіх тіл системи є очевидний, то рівняння теплового балансу варто записувати у вигляді (2.14а). В іншому випадку слід використовувати рівняння (2.14), тоді знак відповіді вкаже напрям теплообміну. Варто також згадати, що в рівняннях теплового балансу фігурують тільки різниці температур. Тож у викладках і при обчисленнях немає потреби переводити температури з °С у К
Слід також взяти до уваги, що теплоємність калориметра за промовчанням не враховується.
Рівень А
| 2.32. |
У калориметрі змішали однакові кількості гарячої води при 70°С і холодної при 10°С. Знайти температуру води після встановлення рівноваги. [40°С] |
||
| 2.33. |
В калориметр із 1,5 кг води при температурі 15°С впускають 200 г водяної пари з температурою 100°С. Визначити температуру, що встановиться. [84,7°С] |
||
| 2.34. |
Свинець масою 1 кг при нагріванні отримав 52,4 кДж теплоти, через що половина його розплавилася. Визначити початкову температуру свинцю. [0°С] |
||
| 2.35. |
Розтоплюючи в печі сніг із початковою температурою –10°С, отримують воду з температурою 20°С . При цьому виявляється, що маса одержаної води в 10 разів перевищує масу спалених дров. Визначити питому теплоту згоряння дров, якщо ККД печі складає 44%. [10 МДж/кг] |
||
| 2.36. |
Свинцева куля без відскоку вдаряє в сталеву плиту зі швидкістю 300 м/с. На скільки градусів нагрівається куля, якщо 40% її кінетичній енергії йде на нагрівання плити та навколишнього повітря? [43°С] |
||
| 2.37. |
У залізний калориметр масою 100 г із 0,5 кг води при температурі 15°С вміщують кусок сплаву свинцю з алюмінієм загальною масою 150 г і температурою 100°С . Визначити маси свинцю й алюмінію в сплаві, якщо в калориметрі встановилася температура 17°С. [42 г і 108 г] |
||
| 2.38. |
В посудину з 0,5 л води при температурі 15°С кинули 50 г мокрого снігу, через що температура в посудині знизилася на 5°С. Визначити масу води, котра містилась у снігові. Втратами тепла знехтувати. [23 г] |
Рівень Б
| 2.39. |
В суміш льоду з водою в калориметрі, котра перебуває в тепловій рівновазі, опустили й увімкнули кип'ятильник потужністю 700 Вт. Через 5,5 хв температура в калориметрі почала збільшуватися зі швидкістю 10 К/хв. Визначити початкові маси льоду і води. Питома теплоємність води 4,19 кДж/(кг·К), питома теплота плавлення льоду 0,33 МДж/кг. [700 г; 300 г] |
||
| 2.40. |
Сталева куля, що вільно падає з висоти 500 м, досягає поверхні землі зі швидкістю 50 м/с. Не враховуючи втрат тепла на нагрівання повітря, знайти, на скільки підвищується температура кулі за час падіння. Питома теплоємність сталі 440 Дж/(кг·К) [8,5°С] |
||
| 2.41. |
Визначити витрату бензину в автомобілі на 1 км шляху на швидкості 60 км/год при потужності і ККД двигуна 16 кВт і 30%. Теплотворність бензину 46 МДж/кг. [70 г/км] |
||
| 2.42. |
В калориметр, який містить 200 см3 води при температурі 100°С вкидають кусочок льоду масою 10 г і температурою 0°С. Визначити температуру, що встановиться в калориметрі. Якою була би відповідь при масі льоду 100 г? [25°С; 0°С] |
||
| 2.43. |
Нагрітий алюмінієвий куб кладуть на лід із температурою 0°С. Визначити початкову температуру куба, якщо в кінцевому стані він повністю занурився в лід. Питома теплота плавлення льоду 335 кДж/кг, питома теплоємність алюмінію 836 Дж/(кг·К), густина льоду 920 кг/м3, густина алюмінію 2,7 г/см3. [136,5°С] |
||
| 2.44. |
Установку, в якій виділяється теплова потужність 30 кВт, охолоджують прокачуванням води, по змійовику з діаметром трубки 15 мм. Вважаючи, що на нагрівання води йде все тепло, що виділяється, визначити швидкість її руху, якщо за час проходження змійовиком вода нагрівається на 15°С. [2,7 м/с] |
||
| 2.45. |
На електроплитці потужністю 600 Вт вода в кількості 1,5 л і з початковою температурою 20°С закипає за 10,5 хв. При цьому 5% води випаровується. Визначити ККД плитки, якщо питома теплоємність води с = 4,2 кДж/(кг·К) і питома теплота пароутворення r = 2,3 МДж/кг. [75 %] |
||
Колові процеси. Теплові двигуни
| 2.46. |
Газ (робоче тіло) в ідеальному тепловому двигуні одержав від нагрівника 500 кДж теплоти при температурі 200°С. Визначити ККД двигуна і кількість теплоти, що передана холодильнику з температурою 20°С. [38%; 310 кДж] |
||
| 2.47. |
Температура нагрівника ідеального теплового двигуна 200°С, а холодильника 11°С. На скільки необхідно збільшити температуру нагрівача для збільшення ККД двигуна на 10%? [94,5°С] |
||
| 2.48. |
|
||
| 2.49. |
Коловий процес в ідеальному газі складається з двох ізобар і двох ізохор, на кожній з яких температура газу змінюється в три рази. Знайти ККД цього циклу. [22%] |
||
| 2.50. |
Із газом у кількості ν молів проводять цикл 1→2→3→4→1, (рис. 50), в якому |
||
| 2.51. |
У паровій машині потужністю 15 кВт за годину спалюють 8 кг вугілля з питомою теплотою згоряння 33 МДж/кг. Температури: котла 200°С, холодильника 60°С. Визначити ККД машини та знайти його відношення до ККД ідеального теплового двигуна з тими самими робочими температурами. [20,5%; 0,7] |
Розділ ІІІ. Пари, рідини та тверді тіла
Молекулярно-кінетичний та термодинамічний методи дозволяють досліджувати не лише гази, а й рідини та тверді тіла – речовини, в яких молекули сильно взаємодіють між собою. При цьому характерні властивості сил міжмолекулярної взаємодії дозволяють пояснити існування різних агрегатних станів речовини (твердого, рідкого та газоподібного) та можливість їхньої зміни.
Далі розглянуто наступне.
3.1. Теоретичні відомості. Молекулярні сили

Атоми й молекули складаються із різнойменно заряджених частинок – ядер та електронів, між якими діють сили притягання та відштовхування, що не однаково швидко змінюються із відстанню r між частинками. Це ілюструє схематичний рис. 3.1.(1), на якому синя, червона та зелена криві відповідають силі притягання fп, відштовхування fв та сумарній силі взаємодії f між двома молекулами. На великій відстані притягання й відштовхування між молекулами, природньо, є скомпенсованим. А при зближенні спочатку швидше зростає притягання, а потім відштовхування, так що на відстані r = r0 порядку розмірів молекул, сили зрівноважуються, а потім стрімко наростає відштовхування. Таким чином, при відхиленні молекул від указаного положення в той, чи інший бік виникає сила, що прагне відновити їхнє початкове розташування. Через це в рідинах і твердих тілах молекули тримаються купи, а їхній тепловий рух має характер малих коливань навколо положень рівноваги. Це пояснює наявність заданого об'єму та форми у твердих тіл. Рідини теж мають власний б'єм, але є текучими, тобто приймають форму посудини, в якій містяться. Це зумовлюється значно слабшим, аніж у твердих тілах, зчепленням між молекулами, через що вони спонтанно ''перескакують'' з одних рівноважних положень у інші, так що рідина завжди щільно прилягяє до стінок посудин.
Для подолання сил зчеплення та розриву зв'язку між молекулами тіла має бути виконана певна робота. Вона називається енергією зв'язку і може виконуватися як за рахунок прикладеної до тіла зовнішньої сили, так і за рахунок кінетичної енергії теплового руху молекул. Тому, залежно від співвідношенням між енергією зв'язку та енергією теплового руху молекул речовина може перебувати в твердому, рідкому чи газоподібному стані та переходити з одного агрегатного стану в інший при зміні температури.
Твердий стан речовини спостерігається, коли в ній енергія зв'язку молекул є набагато більша за кінетичну енергію теплового руху молекул. У такому разі кінетичної енергії вистачає лише на незначні зміщення молекул з рівноважних положень. Тому
|
молекули твердого тіла розміщуються у просторі в правильному геометричному порядку, утворюючи кристалічну структуру (ґратку), і здійснюють лише малі коливання навколо положень рівноваги. |
Це зумовлює зумовлює характерні властивості твердих тіл – здатність зберігати форму та високу міцність.
У газах, напроти, енергія зв'язку молекул є набагато меншою за середню кінетичну енергію теплового руху. Тож сили міжмолекулярного зчеплення не здатні утримувати молекули газу одна біля одної, тож
|
Через це визначальними властивостями газів є здатність заповнювати весь наданий об'єм і велика стисливість.
Рідини займають проміжне становище між твердими тілами та газами. Енергія зв'язку молекул у них перевищує кінетичну енергію теплового руху, але не так сильно, як у твердих тілах. Тому в рідинах, подібно до твердого тіла, молекули розміщені щільно, що пояснює наявність власного об'єму та нестисливість рідин. Але через високу рухливість
|
молекули рідини не мають постійних положень рівноваги й часто переміщуються на значні відстані. |
Цим зумовлена текучість рідин – вони не мають власної форми і щільно заповнюють посудину, в якій знаходяться, так, що, за винятком країв, вільна поверхня рідини завжди є горизонтальна.
Як говорилося, тепловий рух молекул у твердих тілах і рідинах має характер малих коливань навколо положень рівноваги. При підвищенні температури їхня кінетична енергія зростає. Через це збільшується амплітуда теплових коливань і середня відстань між молекулами. Цим пояснюється теплове розширення рідин і твердих тіл, тобто збільшення їх лінійних розмірів l (лінійне розширення) і об'єму V (об'ємне розширення). При невисоких температурах лінійне розширення підпорядковується закону
| \(l={{l}_{0}}+(1+\alpha t)\), |
(3.1) |
де t – температура в °C, l0 – довжина тіла при t = 0°C. Величина \( \alpha \) називається коефіцієнтом лінійного розширення і показує відносну зміну довжини тіла при зміні температури на 1 K (або 1°C):
| \(\alpha =\frac{l-{{l}_{0}}}{{{l}_{0}}t}\) (1/K). |
(3.2) |
Аналогічно змінюється й об'єм тіла при нагріванні:
|
\(V={{V}_{0}}(1+\beta t)\), |
(3.3) |
де V0 – об'єм тіла при t = 0 °C, \(\beta \) – коефіцієнт об'ємного розширення:
|
\(\beta =\frac{V-{{V}_{0}}}{{{V}_{0}}t}\) (1/K). |
(3.4) |
Коефіцієнти теплового розширення \(\alpha \) та \(\beta \) пов'язані між собою співвідношенням
|
\(\beta =3\alpha \). |
(3.5) |
і є табличними характеристиками речовин.
Пароутворення
|
При зміні температури тіла змінюється й співвідношення між кінетичною енергією теплового руху молекул та їхньою енергією зв'язку. Тому залежно від температури та тиску кожна речовина може перебувати в твердому, рідкому чи газоподібному стані й переходити з одного в інший, зокрема, з рідкого в газоподібний. При цьому рідина, що перейшла в газоподібний стан, називається парою, а сам такий перехід – пароутворенням. Існує два види пароутворення – випаровування та кипіння. (Примітка. Деякі речовини можуть переходити з твердого в газоподібний стан, проминаючи рідкий. Цей процес називається сублімацію й тут не розглядається). Випаровування відбувається з вільної поверхні рідини і є зумовлене тим, що в рідинах енергія зв'язку молекул не дуже перевищує середню енергію теплового руху. Через це в рідині при всякій температурі є певна кількість молекул, які здатні долати зв'язок з іншими й виходити назовні, утворюючи пару. При цьому, через віднесення енергії "гарячими" молекулами, рідина охолоджується. Зазвичай це охолодження не є сильним, бо указана втрата енергії значною мірою компенсується через теплообмін із довкіллям. Але за відсутності такого, як от при інтенсивному відкачуванні теплоізольованої колби з водою, охолодження може виявитися настільки сильним, що рідина замерзне – перейде в твердий стан. |
|
Якщо посудину з рідиною щільно закрити, то разом із випаровування буде відбуватися й конденсація – повернення частини молекул пари в рідину. При цьому кількість молекул, які випаровуються, є пропорційна їхній концентрації в рідині, а тих, які конденсуються, – в парі. Тому в закритій посудині кількість молекул, які покидають рідину, спочатку суттєво перевищує кількість тих, що повертаються, і з часом зростає. У такому разі пара називається ненасиченою і, як свідчить дослід, ненасичена пара задовольняє рівняння Клапейрона (1.13), і всі процеси в ній відбуваються, як в ідеальному газі. При невеликій кількості рідини в посудині пароутворення буде переважати конденсацію аж до випаровування всієї рідини, причому пара весь час лишатиметься ненасиченою. Але якщо рідини в посудині багато, то в якийсь момент кількості молекул, які вилітають і повертаються, зрівнюються, і між парою та рідиною встановлюється динамічна рівновага. Пара, що перебуває в динамічній рівновазі зі своєю рідиною, називається насиченою. |
|
При цьому параметри насиченої пари теж задовольняють рівняння Клапейрона, але процеси в ній суттєво відрізняються від таких в ідеальному газі. Причиною є те, що насичена пара існує тільки разом зі своєю рідиною і перебуває в динамічній рівновазі з нею. Тож при будь-якій зміні параметрів стану відповідно змінюється й кількість пари в посудині. Через це тиск насиченої пари при сталій температурі (T = const) не залежить від об'єму: P = const (рис. 3.2а). Це є зумовлено тим, що при зміні об'єму пари динамічна рівновага між нею та рідиною зміщується в бік відновлення концентрації молекул пари, тож і тиску. Тиск почне залежати від об'єму лише після повного випаровування рідини. Тому для насиченої пари закон Бойля-Маріотта (1.16) не виконується.
Так само, хоча параметри пари лишаються пов'язані рівнянням Клапейрона (рівняння (1.13), (1.13а)), для насиченої пари не виконуються й закони Гей-Люссака (1.17) та Шарля (1.19), як показано на рис. 3.2 б,в. Цей позірний парадокс має просте пояснення: в закритій посудині неможливо змінювати стан насиченої пари без зміни її кількості ν, тобто проводити ізопроцеси, для яких за означенням ν = const. |
|
Окрім випаровування, є ще один вид пароутворення в рідинах – кипіння, коли пара утворюється, головно, в об'ємі, а не на поверхні рідини. При кипінні на стінках посудини та в об'ємі рідини виникають бульбашки з насиченою парою, що спливаючи на поверхню, лускають і випускають у посудину велику кількість пари. Існування бульбашок у рідині можливе лише за умови, що тиск пари в них є не менший, ніж тиск з боку рідини. Отже кипіння починається тоді, коли тиск насиченої пари зрівняється із зовнішнім тиском на вільну поверхню рідини, котрий у відкритій посудині збігається із атмосферним тиском. І позаяк тиск насиченої пари при заданій температурі залежить від природи рідини, кожна рідина при заданому тиску має свою температуру кипіння. Зокрема, температура кипіння води при нормальному атмосферному тиску (760 мм.рт.ст.) є однією з "реперних точок" шкали Цельсія і прийнята рівною 100 °С. При збільшені тиску температура кипіння рідини зростає, а при зменшенні зменшується, як схематично показано на рис. 3.3.
|
|
Більшу частину поверхні Землі покривають океани, моря та інші водойми. Тому в атмосфері присутня значна кількість водяної пари, що істотно впливає на клімат та умови життя в різних географічних зонах. Вміст водяної пари в повітрі характеризують його вологістю. Розрізняють абсолютну та відносну вологості. У фізиці абсолютною вологістю називають масу водяної пари в одиниці об'єму повітря, виражену в (г/м3). Інакше кажучи, мірою абсолютної вологості є густина \( \rho \) водяної пари у повітрі.Натомість у метеорології абсолютною вологістю іменують парціальний тиск Р водяної пари в повітрі, виміряний в мм.рт.ст., який ще називають пружністю пари. Варто відмітити, що в інтервалі (0 ÷ 30)°С числові значення Р(мм.рт.ст.) ≈ \(\rho\) (г/м3): відміна складає всього (1 ÷ 5)%). Суб'єктивне відчуття сухості та вологості повітря визначається не власне вмістом водяної пари, а тим, наскільки вона є далекою чи близькою до насичення. Тож, окрім абсолютної, використовують ще й відносну вологість повітря – відношення абсолютної вологості до густини (або парціального тиску) насиченої водяної пари при тій самій температурі:
Тиск насиченої пари спадає при зменшенні температури. Тому зниження температури повітря при незмінній абсолютній вологості призводить до збільшення відносної вологості, й може статися, що за певної температури Tр вона досягне 100%, тобто пара стане насиченою. При цьому почнеться конденсація пари в повітрі та на поверхні предметів. Візуально це проявляється як туман, або випадіння роси.Тож температуру Tр, при якій водяна пара, що міститься у повітрі, стає насиченою, називають точкою роси. Примітка. Величина Tр залежить від вмісту пари у повітрі. При малій абсолютній вологості може статися що Tр < 273 К (0 °С). В такому разі при досягненні температури T = Tр випадає не роса, а іній. |
Поверхня рідини
|
Рідина через рухливість молекул є текучою – не зберігає форми й характеризується лише об'ємом і вільною поверхнею. При цьому на молекули поверхневого шару з боку інших діють сили, що зумовлюють специфічні ефекти: поверхневий натяг, змочування та капілярність. В об'ємі рідини кожна молекула з усіх боків оточена іншими молекулами (рис. 3.4а), дія котрих на неї
На молекули межі поверхневого шару рідини (залитий круг на рис. рис. 3.5, на малих ділянках з боку інших \(F=\sum{{{f}_{i}}}\) і є прямо пропорційна його довжині l:
|
|
де коефіцієнт пропорційності \( \sigma \) (Н/м) є індивідуальною характеристикою рідини й називається коефіцієнтом поверхневого натягу, або просто поверхневим натягом. Отже, коефіцієнт поверхневого натягу даної рідини чисельно дорівнює силі поверхневого натягу, що припадає на одиницю довжини периметра поверхні її дотику зі стінкою посудини. Величина σ, визначається, головно, індивідуальними властивостями рідини і зменшується при нагріванні. Примітка. На поверхневий натяг у рідині впливає також газ над її поверхнею. Але зазвичай цей вплив є неістотним. Для збільшення площі вільної поверхні рідини необхідно виконати відповідну роботу по подоланню поверхневого натягу. При переміщенні малої ділянки \(\Delta {{l}_{i}}\) межі поверхні на невелику відстань \(\Delta {{x}_{i}}\) ця робота дорівнює: \(\Delta {{A}_{i}}={{f}_{i}}\Delta {{x}_{i}}=\sigma \Delta {{S}_{i}}\), де $\Delta {{S}_{i}}=\Delta {{l}_{i}}\Delta {{x}_{i}}$ – зміна площі поверхні рідини, зумовлена цим переміщенням. А для всієї лінії дотику вказана робота становить
де \(\Delta S\) – зміна площі всієї вільної поверхні рідини. Формула (3.8) дозволяє дати альтернативне ''енергетичне'' означення коефіцієнта поверхневого натягу:
Зрозуміло, що при зменшенні з якихось причин цієї площі вже самі сили поверхневого натягу будуть виконувати роботу за рахунок потенційної енергії розтягнутої поверхні рідини, котра зветься вільною поверхневою енергією. |
|
Молекули рідини взаємодіють не лише між собою, а й з молекулами тіла, з яким вона контактує. При цьому спостерігається ефекти змочування та незмочування. При змочуванні краплина рідини розпливається по поверхні тіла (рис. 3.6а), а при незмочуванні – ні (рис. 3.6б).
Змочування спостерігається тоді, коли сила взаємодії молекул твердого тіла з молекулами рідини є більша, ніж сила зчеплення молекул рідини між собою, тобто – ніж сила поверхневого натягу (F > Fн). В іншому випадку (Fн> F) спостерігається незмочування: крапля рідини не розтікається, а лише деформується під дією сили тяжіння. Ступінь змочування чи незмочування визначається величиною крайового кута \( \alpha \) і може бути різним у залежності від природи рідини й тіла, з яким вона контактує, та інших факторів. В елементарній фізиці розглядаються лише повне змочування (коли \(\alpha =0{}^{\circ} \)) і повне незмочування (коли \(\alpha =180{}^{\circ} \)). |
|
Сили, що діють на рідину з боку стінки по периметру меніска, при незмочуванні напрямленні донизу й притискають поверхневий шар до решти рідини, а при змочуванні, напроти, підтягають його догори. Це створює своєрідний "молекулярний тиск" із знаком "+" при незмочуванні та "–"при змочуванні, котрий при заданому поверхневому натягу \(\sigma \) визначається наступними загальними формулами:
Молекулярний тиск спричинює піднімання (при змочуванні) та опускання (при незмочуванні) рівня рідини в капілярі на певну висоту h по відношенню до її рівня в широкій посудині, рис. 3.8. Величина h визначається тією умовою, що різниця гідростатичних тисків у капілярі та посудині має компенсувати додатковий молекулярний тиск (3.9):
(Знак "–" відноситься до випадку незмочування й означає опускання рівня рідини в капілярі). |
Тверде тіло
Завдяки великій енергії зв'язку молекул у твердих тілах, вони мають власну форму й чинять спротив її зміні під дією зовнішніх сил. Це зумовлює специфічні властивості твердого тіла, зокрема пружність і міцність.
При прикладанні сили до закріпленого одним кінцем тіла відбувається його деформація (зміна відстані між молекулами), що супроводжується появою в тілі сил, які прагнуть відновити початкову конфігурацію молекул (див. п. 3.1). Тож після припинення дії порівняно невеликої прикладеної сили тіло повністю відновлює свої розміри та форму. Такі деформації та сили, що при цьому виникають у тілі, називаються пружними деформаціями й силами пружності. При збільшенні прикладаних сил з певного моменту в тілі з'являються пластичні деформації, тобто такі, що не зникають після припинення дії цих сил. А при подальшому збільшенні навантаження настає руйнація тіла.
Через складний характер міжмолекулярної взаємодії зв'язок між прикладеною силою та деформацією твердого тіла, на загал, теж є складним. Але при малих деформаціях ситуація спрощується, бо в такому разі сила взаємодії між молекулами f є прямопропорційна зміні відстані Δr між ними (див. рис. 3.9):
|
|
f = αΔr, |
(3.11) |
де α – силова константа, що визначається індивідуальними властивостями молекул даного тіла.

Вираз (3.11) дозволяє за допомогою простих міркувань встановити зв'язок між деформацією та прикладеною до тіла силою. Для цього розглянемо закріплений стрижень довжиною l і площею перерізу S, до якого прикладено поздовжню силу F (рис. 3.а). Задля зручності приймемо, що стрижень має прямокутний переріз, і молекули в ньому розміщені у вершинах кубічних комірок із ребром r (рис. 3.б), так що на одну молекулу в перерізі припадає площа $S={{r}^{2}}$. У такій моделі стрижень являє собою сукупність N1 = (S/r2) поздовжніх ланцюжків молекул, на кожен з яких діє сила
$f=\frac{F}{{{N}_{1}}}=\frac{F{{r}^{2}}}{S}$,
котра за виразом (3.11) змінює відстань між молекулами на величину
$\Delta r=\frac{F{{r}^{2}}}{\alpha S}$.
Тож, ураховуючи, що на довжині стрижня вкладається N2 = (l/r) молекул, його деформація (зміна довжини) становить
|
$\Delta l=\frac{lrF}{\alpha S}$. |
(3.12) |
Пружня сила Fпр, що виникає в стрижні, має таку саму величину F, тож можна записати
|
${{F}_{\text{пр}}}=k\Delta l$, |
(3.13) |
де коефіцієнт
|
$k=\frac{\alpha }{r}\cdot \frac{S}{l}$ |
(3.14) |
називається жорсткістю стрижня й визначається властивостями його речовини та розмірами й формою (площею перерізу та довжиною). Якісно так є й для тіла довільної форми.
Таким чином
сила пружності, що виникає в тілі є прямо пропорційна до величини його деформації.
Це твердження в свій час було встановлене на досліді й відоме як закон Гука.
Сила пружності Fпр в тілі створюється всією сукупністю молекул і є розподілена по всій площі перерізу стрижня. Тому для характеристики механічного стану деформованого тіла, крім сили, використовують механічну напругу \(\sigma \) – силу, що припадає на одиницю площі поперечного перерізу тіла:
|
\(\sigma =\frac{F}{S}\). |
(3.15) |
Механічна напруга, як і тиск, вимірюється в паскалях (Н/м2). Зв'язок між деформацією та механічною напругою безпосередньо випливає з виразу (3.12) і записується у вигляді:
|
\(\frac{\Delta l}{l}=\frac{\sigma }{E},\) |
(3.16) |
де величина E = (α/r), що залежить від внутрішньої будови тіла та зв'язку між молекулами, називається модулем пружності або модулем Юнґа і є табличною характеристикою кожної твердої речовини.
Таким чином,
відносне видовження тіла є прямо пропорційне механічній напрузі в ньому.

Як зазначалося на початку, закон Гука виконується тільки в певному інтервалі прикладених до тіла сил. Причина полягає в тому, що при великому розтязі порушується пряма пропорційність між зміщеннями з рівноважних положень Δr та силою взаємодії молекул тіла f . Це схематично відображує рис. 3.10, з якого зрозуміло, що зв'язок між механічною напругою σ = (F/S) і відносною деформацією ε = (Δl/l)) є лінійним (закон Гука) тільки до певного значення ε1. Далі в інтервалі ε1÷ ε2 лінійність порушується, хоча деформація ще лишається пружною. Але потім (область ε2÷ ε3) у тілі з'являються пластичні (залишкові) деформації. Напруга, при якій вони з'являються, називається межею пружності. А ще далі при певній деформації ε3 починається видовження тіла без збільшення напруги (''текучість'') і врешті решт — розрив. Напруга \({{\sigma }_{м}}\), при якій стається розрив тіла називається границею міцності.
Говорячи про закон Гука, слід зауважити, що формули (3.13)1– (3.16) є чинні тільки для розтягу чи стискання тіла сталого перерізу – брусків і стрижнів. Але його загальний зміст справджуються й для тіл іншої форми та для інших видів деформації, до прикладу таких, як зсув або кручення.
Для надійного і безпечного функціонування будівельних та інженерних споруд і конструкцій граничні припустимі напруги в них \({{\sigma }_{\text{гр}}}\) мають бути набагато меншими, ніж \({{\sigma }_{м}}\). Тому при розрахунках і виготовленні конструкцій в кожному випадку враховується відповідний запас міцності
|
η =\(\frac{{{\sigma }_{м}}}{{{\sigma }_{\text{гр}}}}\). |
(3.17) |
Співвідношення між величинами на різних ділянках графіка рис. 3.10 та граничні параметри для різних матеріалів істотно відрізняються, що визначає область їхнього практичного використання. При цьому, крім міцності, важливу роль відіграють крихкість і пластичність матеріалів. У крихких речовинах (таких, як чавун, скло та ін.) \({{\sigma }_{\text{п}}}\approx {{\sigma }_{м}}\), тобто при деформації вони лишаються пружними аж до руйнування. Пластичні речовини (до прикладу, свинець), напроти, мають малу межу пружності (\({{\sigma }_{\text{п}}}\ll{{\sigma }_{м}}\)). Тому в них зазвичай спостерігаються тільки пластичні деформації, тож їм легко надавати потрібної форми штампуванням або куванням.
3.2. Приклади розв’язування задач
Представлені нижче приклади поділені за наступними темами:
Властивості пари, вологість повітря
Властивості пари, вологість повітря
Задача 3.1. На шальки важільних терезів поставили однакові закриті посудини із сухим та з вологим повітрям при однакових тиску й температурі. Визначити, яка з посудин переважить.
Задача 3.2. Абсолютна вологість повітря вдень при температурі t1 = 30°C дорівнює ρ1 = 15 г/м3. Визначити його відносну вологість φ1 вдень і абсолютну ρ2 та відносну φ2 вологості вночі при температурі t2 = 10°C.
Задача 3.3. Людина в окулярах входить знадвору, де температура повітря t1 = 5 °C, до приміщення з температурою t2 = 25 °C. Визначити, при якій найбільшій відносній вологості повітря в приміщенні \( {{\varphi }_{\m }}\) окуляри не запітніють.
Задача 3.4. Увечері температура повітря була t1 = 20°C при відносній вологості φ1 = 70 %, а під ранок знизилася до t2 = 10°C . Визначити масу роси m, що випала з кожного кубометра повітря.
Задача 3.5. У відкачаному циліндрі з поршнем міститься V1 = 10 л вологого повітря при тиску P1 = 13,3 кПа, температурі t = 20°C і вологості φ = 70%. Визначити тиск P2 повітря в циліндрі після того, як його об'єм при сталій температурі зменшили в k = 10 разів.
Задача 3.6. Дистильовану воду без розчиненого повітря в посудині з чистими й гладкими стінками можна нагріти до температури, що суттєво перевищує 100°С. Така ''перегріта'' вода при якомусь збуренні, приміром слабкому поштовху чи потраплянні порошинки, вибухоподібно закипає одночасно по всьому об'єму й одразу набуває стандартн0ї температури кипіння. Знайти масу пари mп, що в таким чином утворюється з перегрітої до t = 120°С води масою m = 1 кг води в закритій посудині об'ємом V = 1,2 л. Питома теплоємність води с = 4,2 кДж/(кг·К), питома теплота пароутворення r = 2,3 MДж/кг.
========================
Задача 3.1
На шальки важільних терезів поставили однакові закриті посудини із сухим та з вологим повітрям при однакових тиску й температурі.
Визначити,
яка з посудин переважить.
|
Дано: \( V_{1}=V_{2}\)
\(P_{1}=P_{2}\)
\( {T}_{1}=T_{2}\)
|
|
\( {m_{1}}/m_{2}\) - ?
|
Розв’язання
За однакового тиску, об'єму та температури загальні кількості молекул в обох посудинах, згідно з формулою (1.13), теж однакові. Але, тоді як сухе повітря майже повністю складається з азоту N2 (молярна маса 28 г/моль) і кисню О2 (молярна маса 32 г/моль), у вологому частина вказаних молекул є заміщена легшими молекулами води H2O (молярна маса 18 г/моль). Отже, переважить посудина із сухим повітрям.
| Задача 3.2 |
Абсолютна вологість повітря вдень при температурі t1 = 30°C дорівнює ρ1 = 15 г/м3.
Визначити
його відносну вологість φ1 вдень і абсолютну ρ2 та відносну φ2 вологості вночі при температурі t2 = 10°C.
|
Дано: t1 = 30°C
t2 = 10°C
ρ1 =15 г/м3
|
| φ1-?, φ2-?, ρ2-? |
Розв’язання
Відносна вологість дорівнює відношенню абсолютної вологості ρ до густини насиченої водяної пари ρн, що визначається з рівняння Клапейрона (1.14) через задану температуру й тиск Рн як
${{\rho }_{\text{н}}}=\frac{{{P}_{\text{н}}}M}{RT}$.
Тож, узявши з таблиць значення Р1н = 31,8 мм.рт.ст. при температурі 30°C, дістанемо ρ1н = 30,3 г/м3 , і за означенням (3.6) Р2н = 9,2 мм.рт.ст. для 10°C, дістанемо:
φ1 = 49,5%.
Так само за таблицями при температурі 10°C ρ2н = 9,6 г/м3, що менше за задану величину ρ1. Це означає, що з кожного кубометра повітря випаде 5, 4 г роси, й воно буде насиченим і матиме вологість
ρ2 = 9,6 г/м3 і φ2 = 100%.
Задача 3.3
Людина в окулярах входить знадвору, де температура складає t1 = 5 °C, до приміщення з температурою t2 = 25 °C.
Визначити,
при якій найбільшій відносній вологості повітря в приміщенні \( {{\varphi }_{\m }}\) окуляри не запітніють.
|
Дано: \( t_{1}\) = 5 °C
\( {t}_{2}\) = 25 °C
|
|
\( {{\varphi }_{\max }}\) - ?
|
Розв’язання
Після того, як людина увійшла до приміщення, скельця окулярів ще деякий час зберігають температуру близьку до t1 = 5 °C. Зрозуміло, що прилеглий шар повітря набуває такої самої температури. При цьому окуляри не запітніють, якщо на скельцях не почнеться конденсація водяної пари, тобто за умови
|
|
\( \rho \le {{\rho }_{н1}}\), |
(1) |
де ρ і ρн1 – абсолютна вологість повітря в кімнаті та густина насиченої водяної пари при температурі t1, відповідно. Відтак, виразивши в цьому співвідношенні за означенням (3.6) величину ρ через відносну вологість φ повітря в кімнаті та густину насиченої пари ρн2 при температурі t2, для максимальної допустимої відносної вологості отримаємо:
|
\({{\varphi }_{\max }}=\frac{{{\rho }_{н1}}}{{{\rho }_{н2}}}.\) |
(3) |
За наявності таблиць густин насиченої пари можна відразу обчислити відповідь. В іншому випадку спочатку з рівняння Клапейрона (1.14) слід виразити величини ρ = (m/V) через відповідні тиски й температури та отримати:
\(\varphi_{max}=\frac{P_{н1}}{P_{н2}}\cdot\frac{T_{2}}{T_{1}}\).
Відтак, взявши з таблиць значення Pн1 = 0,87 кПа, Pн2 = 3,17 кПа, отримаємо
\(\varphi_{max}\approx0,29\) = 29 %.
Задача 3.4
Увечері температура повітря була t1 = 20°C при відносній вологості \(\varphi_{1}\) = 70 %, а під ранок знизилася до t2 = 10°C.
Визначити
масу роси m, що випала з кожного кубометра повітря.
|
Дано: \(t_{1}\) = 20 °C
\(\varphi_{1}\) = 70 %
\(t_{2}\) = 10 °C
|
|
m - ?
|
Розв’язання
Шукана величина m (кг/м3) дорівнює різниці густин водяної пари (абсолютних вологостей) при температурах t1 і t2:
|
|
\({m}=\rho_{1}-\rho_{2}\). |
|
Роса випадає, коли водяна пара в повітрі стає насиченою, тобто
|
|
\(\rho_{2}=\rho_{н2}\), |
|
а величина \(\rho_{1}\), відповідно до означення (3.1), дорівнює
|
|
\(\rho_{1}=\varphi_{1}\rho_{н1}\). |
|
Отже,
|
|
\({m}=\varphi_{1}\rho_{н1}-\rho_{н2}\). |
|
Тож, виразивши (m/V) через тиски насиченої пари з рівняння Клапейрона (1.14), отримаємо:
\({m}=\frac{M}{R}\left(\frac{\varphi_{1}P_{н1}}{T_{1}}-\frac{P_{н2}}{T_{2}}\right)\).
Відтак, узявши з таблиць Pн1 = 2,33 кПа і Pн2 = 1,22 кПа та R = 8,31 Дж/(моль·К) і M = 18 г/моль, знайдемо:
m ≈ 2,7 г.
Задача 3.5
У відкачаному циліндрі з поршнем міститься V1 = 10 л вологого повітря при тиску P1 = 13,3 кПа, температурі t = 20°C і відносній вологості φ = 70 %.
Визначити
тиск в P2 повітря в циліндрі після того, як його об'єм при сталій температурі зменшили в k = 10 разів.
|
Дано: V1 = 10 л
P1 = 13,3кПа
t = 20 °C
φ = 70 %
k = 10
|
|
P2 - ?
|
Розв’язання
Може здатися, що задача є тривіальною, позаяк за законом Бойля-Маріотта добуток тиску на об'єм газу є сталим. Але це не так, бо в циліндрі міститься суміш сухого повітря та водяної пари, тиск якої при досягненні насичення перестає залежати від об'єму. Тож поведінку сухого повітря та пари треба аналізувати окремо.
Позначимо парціальний тиск сухого повітря як Pп і водяної пари як Pв . Тоді за законом Дальтона (1.12) початковий тиск сухого повітря
Pп1 = P1 – Pв1,
де початковий тиск пари Pв1 визначається вологістю повітря φ та тиском насиченої пари Рн:
|
|
Pв1 = φPн. |
(1) |
Тож, ураховуючи означенням (3.6),
|
|
\({P}_{п1}=P_{1}-\varphi_{1}P_{н}\). |
(2) |
За умовою повітря в циліндрі стискається ізотермічно, тому тиск і об'єм змінюються за рівнянням (1.16б):
$\frac{{{P}_{\text{2}}}}{{{P}_{\text{1}}}}=\frac{{{V}_{1}}}{{{V}_{2}}}\quad \Rightarrow \quad {{P}_{\text{2}}}=k{{P}_{\text{1}}}$, де k = $\frac{{{V}_{1}}}{{{V}_{2}}}$.
Звідси, врахувавши співвідношення (2), визначимо тиск сухого повітря:
|
|
\({P}_{п2}=k(P_{1}-\varphi_{1}P_{н}) \). |
(3) |
Водяна пара в циліндрі теж стискається, але її парціальний тиск Pв не може бути більшим за тиск насиченої пари Pн. Ця величина, згідно з означенням (3.6), всього в (1/φ) ≈ 1,4 раза перевищує початковий тиск Pв1, тоді як об'єм зменшується в k = 10 разів. Це означає, що задовго до закінчення стискування вологого повітря пара почне конденсуватися при сталому парціальному тиску Pв2 = Pн. Величина Pн є табличною. Тож з урахуванням виразу (3) шуканий кінцевий тиск у циліндрі Р2 = Pп2 + Pв2 дорівнює:
\({P}_{2}=k(P_{с1}-\varphi_{1}P_{н})+P_{н}\).
За таблицями при t = 20 °C Pн = 2,34 кПа. Тож, підставивши цю та задані в умови величини в отриманий вираз, дістанемо наступну відповідь:
P2 = 119 кПа.
З приводу отриманого результату варто зауважити таке. Хоча стискання повітря в циліндрі відбувалося при сталій температурі, тобто ізотермічно, при десятикратному зменшенні об'єму тиск збільшився тільки в 9 разів. Але це зовсім не означає порушення закону Бойля-Маріотта, тому що в даному випадку ізотермічне стискання не було ''ізопроцесом'', бо через конденсацію пари кількість газу не лишалася сталою.
Дистильовану воду без розчиненого в ній повітря в посудині з дуже чистими й гладкими стінками можна з певними пересторогами нагріти до температури, що суттєво перевищує 100°С. Така ''перегріта'' вода при якомусь збуренні, приміром слабкому поштовху чи потраплянні порошинки, вибухоподібно закипає одночасно по всьому об'єму й одразу набуває ''нормальної'' температури кипіння.
Знайти
масу пари mп, що в таким чином утворюється з перегрітої до t = 120°С води масою m = 1 кг в закритій посудині об'ємом V = 1,2 л. Питома теплоємність води с = 4,2 кДж/(кг·К), питома теплота пароутворення r = 2,3 MДж/кг.
|
Дано: m = 1 кг t = 120°С V = 1,2 л с = 4,2 кДж/(кг·К) r = 2,26 МДж/кг
|
|
mп - ?
|
Розв’язання
В описаному процесі пара утворюється за рахунок енергії, яку втрачає вся вода при охолоджені до "нормальної" температури. Отже, згідно з формулами (2.15) і (2.17),
$cm\Delta t=r{{m}_{\text{п}}}$ $\Rightarrow $ ${{m}_{\text{п}}}=\frac{cm\Delta t}{r}$
де Δt = 20°С – величина ''перегрітості'' води.
Обчислення дають
m = 36,5 г.
Проте ставити на цьому ''крапку'' було би необачно. Пара утворюється при температурі t0 = 100°С в замкненому об'ємі Vп = 0,2 л, тож згідно з таблицями її максимальний парціальний тиск (тиск при насиченні) складає P0 ≈100 кПа (760 мм.рт.ст.). Тому для контролю визначимо з рівняння Клапейрона (1.14) максимальну можливу масу пари за таких умов:
${{m}_{\max }}=\frac{{{P}_{0}}{{V}_{\text{п}}}M}{R{{T}_{0}}}$ ≈ 116 г.
Таким чином, отримане значення m = 36,5 г є коректним.
Поверхневі явища, капілярність
При розгляді поверхневого натягу в плівці рідини не слід забувати, що вона має дві поверхні й дві лінії дотику з твердим тілом. Це призводить до "подвоєння" сили поверхневого натягу, поверхневої енергії, роботи по зміні площі поверхні, тощо.
При обчисленні висоти підняття та ваги рідини в капілярі не враховувано викривлення меніска й прийнято g = 10 м/с2 .
Задача 3.7. Визначити точність дозування мікстури за допомогою піпетки з діаметром отвору d = 1 мм. Густина ліків \(\rho=1\) г/см3, поверхневий натяг \(\sigma=60\) мН/м.
Задача 3.8. Визначити роботу A, необхідну для видування мильної бульби діаметром d = 10 см. Поверхневий натяг мильного розчину \(\sigma=40\) мН/м.
Задача 3.9. Дві вертикальні паралельні скляні пластини, розміщені на відстані d = 0,5 мм одна від одної, опустили на невелику глибину в посудину з водою. Визначити висоту підняття h води між пластинами відносно її рівня в посудині. Поверхневий натяг води \(\sigma\) = 74 мН/м, густина \(\rho\) = 1 г/м3.
Задача 3.10. Два легкі кубики з ребром a = 2 см із змочуваної речовини, один чистий, а інший змащений жиром, опустили на воду. Визначити різницю глибин занурення кубиків \(\Delta{h}\). Поверхневий натяг води \(\sigma\) = 74 мН/м.
Задача 3.11. При вертикальному зануренні капілярної трубки діаметром d = 0,5 мм у посудину з водою (поверхневий натяг σ = 74 мН/м) вода піднялася на висоту h = 2,5 см над рівнем у посудині. Визначити радіус кривини R меніска (вільної поверхні води в капілярі).
++++++++++++++++++++++++++++++++
Задача 3.7
Визначити
точність дозування мікстури за допомогою піпетки з діаметром отвору d = 1 мм. Густина ліків \(\rho=1\) г/см3, поверхневий натяг \(\sigma=60\) мН/м.
|
Дано: d = 1 мм = 10-3 м
\(\rho=1\) г/см3
\(\sigma=60\) мН/м
|
|
V1 - ?
|
Розв’язання
 Точність дозуванні рідини піпеткою визначається об'ємом однієї краплі V1, що відривається від носика піпетки (рис. 7). Відрив краплі настає, коли її вага зрівняється з силою поверхневого натягу F, яка діє по лінії дотику рідини з краєм отвору піпетки:
Точність дозуванні рідини піпеткою визначається об'ємом однієї краплі V1, що відривається від носика піпетки (рис. 7). Відрив краплі настає, коли її вага зрівняється з силою поверхневого натягу F, яка діє по лінії дотику рідини з краєм отвору піпетки:
mg = F.
Сила поверхневого натягу, згідно з формулою (3.2),
\({F}=\sigma{l}=\sigma\pi{d}\),
а маса краплі \(m=\rho{V_{1}}\). Тож дістаємо наступну відповідь:
\(\rho{V_{1}}g=\pi{d}\sigma\) \(\Rightarrow\) \(V_{1}=\frac{\pi{d}\sigma}{\rho{g}}\) = 19 мм3.
Задача 3.8
Визначити
роботу A, необхідну для видування мильної бульби діаметром d = 10 см. Поверхневий натяг мильного розчину \(\sigma=40\) мН/м.
|
Дано: d = 10 см
\(\sigma=40\) мН/м
|
|
A - ?
|
Розв’язання
При видуванні мильної бульби необхідно виконувати роботу проти сил поверхневого натягу. Згідно з формулою (3.3) для збільшення площі вільної поверхні рідини на величину \(\Delta{S}\) треба виконати роботу
\(A=\sigma\Delta{S}=\sigma(S_{2}-S_{1})\).
При видуванні бульби початкова площа поверхні S1 = 0, а кінцева S2 = 2S, де \(S=\pi{d^{2}}\) – площа поверхні сфери діаметром d. (Подвоєння у виразі S2 спричинюється тим, що плівка має дві поверхні – зовнішню та внутрішню). Отже,
A = 2πd2σ= 2,5 мДж.
Задача 3.9
Дві вертикальні паралельні скляні пластини, розміщені на відстані d = 0,5 мм одна від одної, опустили на невелику глибину в посудину з водою (рис. 9).
Визначити
Визначити висоту підняття h води між пластинами відносно її рівня в посудині. Поверхневий натяг води \(\sigma\) = 74 мН/м, густина \(\rho\) = 1 г/м3.
|
Дано: d = 0,5 мм
σ = 74 мН/м
ρ = 1 г/м3
|
|
h - ?
|
Розв’язання
 Пластини утворюють капіляр. Внаслідок змочування вода між пластинами буде підніматися, доки її вага mg не скомпенсує силу поверхневого натягу F, яка діє по лініях дотику води з внутрішніми поверхнями пластин (на рис. 9 ці лінії проходять через точки 1,2 перпендикулярно до площини рисунка). Отже, при рівновазі
Пластини утворюють капіляр. Внаслідок змочування вода між пластинами буде підніматися, доки її вага mg не скомпенсує силу поверхневого натягу F, яка діє по лініях дотику води з внутрішніми поверхнями пластин (на рис. 9 ці лінії проходять через точки 1,2 перпендикулярно до площини рисунка). Отже, при рівновазі
|
|
mg = F. |
(1) |
Якщо позначити ширину пластини як l, то
|
|
\({F}=\sigma\cdot{2l}\), |
|
а маса води в капілярі
\({m}=\rho{V}=\rho{dlh}\).
Підставивши ці вирази умову рівноваги (1), дістанемо відповідь:
$ h=\frac{2\sigma }{\rho dg}$ = 3 см.
Задача 3.10
Два легкі кубики з ребром a = 2 см із змочуваної речовини, один чистий, а інший змащений жиром, опустили на воду.
Визначити
різницю глибин занурення кубиків \(\Delta{h}\). Поверхневий натяг води \(\sigma\) = 74 мН/м.
|
Дано: a = 2 см
\(\sigma\) = 74 Н/м
|
|
\(\Delta{h}\) - ?
|
Розв’язання
 З умови зрозуміло, що один кубик (чистий) змочується, а інший (змащений) не змочується. Тому сили, що діють на воду на лінії дотику з кубиком, у першому випадку напрямлені вгору, а у другому – вниз. Відповідно, з боку води на кубики діють сили поверхневого натягу Fн, що напрямлені протилежно: для змоченого кубика вниз (рис. 10а), а для не змоченого – вгору (рис. 10б). Тому чистий кубик буде занурений більше, ніж змащений.
З умови зрозуміло, що один кубик (чистий) змочується, а інший (змащений) не змочується. Тому сили, що діють на воду на лінії дотику з кубиком, у першому випадку напрямлені вгору, а у другому – вниз. Відповідно, з боку води на кубики діють сили поверхневого натягу Fн, що напрямлені протилежно: для змоченого кубика вниз (рис. 10а), а для не змоченого – вгору (рис. 10б). Тому чистий кубик буде занурений більше, ніж змащений.
Умови рівноваги кубиків мають вигляд:
|
|
\({F}_{A1}=mg+F_{н}\), \({F}_{A1}=mg-F_{н}\) |
(1) |
Різницю глибин занурення \(\Delta{h}=h_{1}=h_{2}\) знайдемо, виразивши з системи (1) різницю значень архімедової сили:
\({F}_{A1}-F_{A2}=2F_{н}\).
Архімедова сила FА1 = \(\rho(V_{1}-V_{2})\), а сила поверхневого натягу Fн = \(\sigma{l}\), отримаємо:
\(\rho(V_{1}-V_{2})g=2\sigma{l}\).
Різниця об'ємів зануреної частини кубиків дорівнює Δha2, а довжина лінії дотику води до кубика l = 4a, отже
\(\rho\Delta{h}a^{2}g=2\sigma\cdot{4a}\) \(\Rightarrow \) \(\Delta{h}=\frac{8\sigma}{\rho{ag}}\) = 3 мм.
Задача 3.11. При вертикальному зануренні капілярної труби діаметром d = 0,5 мм у посудину з водою (густина ρ = 1 г/см3, поверхневий натяг σ = 73 мН/м) вода піднялася на висоту h = 2,5 см над рівнем у посудині.
Визначити
радіус кривини R меніска (вільної поверхні води в капілярі).
|
Дано: d = 0,5 мм h = 2,5 см ρ = 1 г/см3 σ = 74 мН/м |
|
R - ? |
Розв'язання
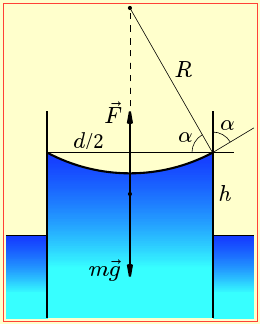
Поставлене в умові завдання означає, що радіус кривини меніска не збігається із радіусом трубки r = d/2, як це мало би бути при повному змочуванні (п. 3.1). Про це свідчить і невідповідність заданій величині h, яка за формулою (3.10) мала складати
${h}'=\frac{4\sigma }{\rho gd}\approx 6\text{ см}\text{.}$
Це означає, що змочування трубки водою є неповним, і меніск є не півсферою з радіусом трубки, а сферичним сегментом із іншим радіусом кривини R і відповідним крайовим кутом α, рис. 11. Через це вага піднятої води mg = ρVg компенсується не всією силою поверхневого натягу Fн, а лишень її вертикальною складовою, величина котрої, згідно с формулою (3.7) і рис.11, складає
$F=\sigma l\cos \alpha $.
Отже,
$\rho Vg=\sigma l\cos \alpha $.
Звідси, врахувавши, що об'єм води в стовпчику $V=\pi {{r}^{2}}h, довжина контуру меніска \text{ }l=2\pi r\text{ i }\cos \alpha =\left( {r}/{R}\; \right)$, після спрощень отримаємо наступну відповідь:
$R=\frac{2\sigma }{\rho gh}$ = 0,6 мм,
що в 2,4 раза перевищує радіус трубки.
В отриманому результаті може здатися несподіваним те, що величина R не залежить від радіуса капіляра. Але в цьому немає нічого дивного, позаяк викривленість меніска залежить від ступеня змочування трубки водою, що визначається не розмірами, а фізичними властивостями рідини та речовини трубки.
Закон Гука, механічні властивості твердих тіл
Задача 3.12. Тягар маси m = 5 кг починають підіймати з підлоги на гумовому шнурі діаметром d = 5 мм. Визначити початкову довжину шнура l0, якщо на момент відриву вантажу від підлоги вона шнура складала l = 1,5 м. Модуль Юнга гуми E = 3,74 МПа.
Задача 3.13. Тягач має буксирувати автомобіль маси m = 1 т вгору по дорозі з ухилом α = 10° за допомогою конопляного каната діаметром d = 7 мм. Визначити максимальне можливе стартове прискорення am тягача при границі міцності каната \(\sigma\) = 80 МПа. Силами тертя та опору знехтувати.
Задача 3.14. Визначити найбільшу висоту будинку hm, який можна вибудувати із запасом міцності k = 3 з цегли густиною \(\rho=2,5\) г/см3 і границею міцності σ = 5 МПа.
Задача 3.15. Визначити, яку роботу треба виконати, аби вдвічі розтягнути гумовий джгут довжиною l =1 м і перерізом 1 см2, якщо його модуль пружності складає E = 10 МПа. Зміною об'єму джгута при розтяганні знехтувати. [500 Дж ].
Задача 3.16. Між двома розташованими на відстані L = 2 м одна від одної стінками натягнуто й закріплено на однаковій висоті залізний (модуль пружності Е = 2 ГПа) дріт діаметром d = 1 мм. Визначити, на яку відстань h опуститься підвішений посередині тягар масою 2,5 кг.
================
Задача 3.12
Тягар маси m = 5 кг починають підіймати з підлоги на гумовому шнурі діаметром d = 5 мм.
Визначити
початкову довжину шнура l0, якщо на момент відриву тягаря від підлоги вона складала l = 1,5 м. Модуль Юнга гуми E = 3,74 МПа.
|
Дано: m = 5 кг
d = 5 мм
l= 1,5 м
E = 3,74 МПа
|
|
l0 - ?
|
Розв’язання
Згідно із законом Гука (3.16)
|
|
$l-{{l}_{0}}={{l}_{0}}\frac{\sigma }{E}$ $\Rightarrow $ ${{l}_{0}}=\frac{l}{1+\left( {\sigma }/{E}\; \right)}$, |
|
де механічна напруга (3.15) в шнурі, що створюється вагою тягаря, визначається як
|
|
$\sigma =\frac{4mg}{\pi {{d}^{2}}}$. |
|
Тож урахувавши діаметр шнура, отримуємо відповідь:
\({l}_{0}=\frac{l}{1+(4mg/\pi{d^{2}}E)}\) = 0,9 м.
Задача 3.13
Тягач має буксирувати автомобіль маси m = 1 т вгору по дорозі з ухилом α = 10° за допомогою конопляного каната діаметром d = 7 мм.
Визначити
максимальне можливе стартове прискорення am тягача при границі міцності каната \(\sigma\) = 80 МПа. Силами тертя та опору знехтувати.
|
Дано: α = 10°
m = 1 т
d = 7 мм
\(\sigma_{m}\) = 80 МПа
|
|
am - ?
|
Розв’язання

За другим законом Ньютона прискорення а автомобіля дорівнює відношенню рівнодійної сили натягу каната F та паралельної до дороги складової сили тяжіння mg·sinα (див. схематичний рис. 13) до маси:
|
|
$a=\frac{F}{m}-g\cdot \sin \alpha $. |
(1) |
Отже, як і має бути, при заданому ухилі дороги та масі авто його теоретично можливе максимальне прискорення am залежить тільки від гранично допустимої величини натягу каната Fm, котра визначається його перерізом $S=(\pi {{d}^{2}}/4)$ і границею міцності ${{\sigma }_{m}}$, як
${{F}_{m}}=\frac{\pi {{d}^{2}}{{\sigma }_{m}}}{4}$.
Отже, підставивши цю величину у вираз (1), отримаємо наступну відповідь
${{a}_{m}}=\frac{\pi {{d}^{2}}{{\sigma }_{m}}}{4m}-g\cdot \sin \alpha $ = 1,4 м/с2
Задача 3.14
Визначити
найбільшу висоту будинку hm, який можна вибудувати із запасом міцності k = 3 з цегли густиною \(\rho=2,5\) г/см3 і границею міцності σ = 5 МПа.
|
Дано: k = 3
σ = 5 МПа
\(\rho=2,5\) г/см3
|
|
hm - ?
|
Розв’язання
 Розглянемо якийсь фрагмент стіни будинку площею основи S (рис. 14). Механічна напруга в цеглі на заданому рівні визначається вагою частини стіни, що лежить вище. Тож найбільшою вона є біля основи й при висоті будинку h складає
Розглянемо якийсь фрагмент стіни будинку площею основи S (рис. 14). Механічна напруга в цеглі на заданому рівні визначається вагою частини стіни, що лежить вище. Тож найбільшою вона є біля основи й при висоті будинку h складає
|
|
\(\sigma=\frac{\rho{hSg}}{S}=\rho{hg}\). |
(1) |
За умовою максимальна допустима напруга дорівнює (σм/k), тому найбільша можлива висота будинку складає
\({h}_{m}=\frac{\sigma_{м}}{k\rho{g}}\) = 68 м.
Визначити,
яку роботу треба виконати, аби вдвічі розтягнути гумовий джгут довжиною l = 1 м і перерізом S = 1 см2, якщо його модуль пружності складає E = 10 МПа. Зміною об'єму джгута при розтяганні знехтувати.
|
Дано: l =1 м S = 1см2 E = 10 МПа |
|
A - ? |
Розв’язання
Із механіки відомо, для збільшення довжини пружного тіла довжини l на задану величну Δl, треба виконати роботу
|
|
$A=\frac{1}{2}F\Delta l$, |
(1) |
де F – сила, що створює вказаний розтяг і, відповідно до закону Гука (3.16) та виразу (3.15), дорівнює
$F=SE\frac{\Delta l}{l}$.
Відтак вираз (1) набуває вигляду:
$A=\frac{\sigma S{{l}^{2}}}{2\Delta l}$.
Звідси, врахувавши, що за умовою Δl = l, отримуємо відповідь:
$A=\frac{lSE}{2}$ = 500 Дж.
Між двома розташованими на відстані L = 2 м одна від одної стінками натягнуто й закріплено на однаковій висоті залізний (модуль пружності Е = 2 ГПа) дріт діаметром d = 1 мм.
Визначити,
на яку відстань h опуститься підвішений посередині тягар масою 2,5 кг.
|
Дано: d = 1 мм L = 2 м m = 2,5 кг Е = 200 ГПа |
|
h - ? |

Розв’язання
Підвішений тягар буде опускатися, доки рівнодійна ${{\vec{F}}_{0}}$ сил натягу в підвісах $\vec{F}$, ${\vec{F}}'$ не скомпенсує вагу тягаря $m\vec{g}$, як показано на схематичному рис. 16. Тож, позначивши задля зручності початкову довжину половини підвісу як (L/2) = l0, а її розтяг як Δl, для переміщення тягаря h = ОО′, як видно з рис. 16, можна записати:
${{h}^{2}}={{\left( {{l}_{0}}+\Delta l \right)}^{2}}-l_{0}^{2}=2{{l}_{0}}\Delta l+{{\left( \Delta l \right)}^{2}}$.
При заданих в умові значеннях ваги тягаря та модуля пружності дроту його видовження достеменно є малим, а величина ($\Delta l$)2 – неістотною. Тож реально
|
|
${{h}^{2}}=2{{l}_{0}}\Delta l$. |
(1) |
Отже, аби знайти відповідь задачі, треба обчислити розтяг підвісу Δl, котрий за співвідношенням (3.16) дорівнює
|
$\Delta l=\frac{\sigma }{E}{{l}_{0}}$. |
(2) |
де механічна напруга σ дорівнює відношенню сили натягу F до площі перерізу дроту S і складає:
$\sigma =\frac{4F}{\pi {{d}^{2}}}$.
Із рисунка розуміло, що
$\frac{F}{\left( mg/2 \right)}=\frac{{{l}_{0}}}{h}\quad \Rightarrow \quad F=\frac{mg{{l}_{0}}}{2h}$
Отже,
$\sigma =\frac{2mg{{l}_{0}}}{\pi {{d}^{2}}h}$
і за формулою (2)
$\Delta l=\frac{2mgl_{0}^{2}}{\pi {{d}^{2}}hE}$.
Відтак, підставивши цезначення у вираз (1) і врахувавши, що 2l0 =L, після елементарних перетворень отримаємо наступну відповідь:
$h=L\sqrt[3]{\frac{mg}{2\pi {{d}^{2}}E}}$ = 2,5 см.
Щодо наведеного розв'язку варто зауважити, що робочий рисунок і подальші викладки передбачають строго горизонтальне натягнення дроту, що є принципово неможливим через його провисання під власною вагою. Але, враховуючи малу масу дроту (порядку 10 г), воно не спричинює помітного впливу на результат.
3.3. Задачі для самостійної роботи
Пропоновані задачі згруповано по наступних темах:
Властивості пари, вологість повітря
Поверхневі явища, капілярність
Закон Гука, механічні властивості твердих тіл
Властивості пари, вологість повітря
Якщо потрібну для розв'язування задачі густину насиченої пари \(\rho_{н}\) не вказано в умові, то вона визначається з рівняння Клапейрона (1.13) за табличним значенням парціального тиску Pн.
Рівень А
|
3.17. |
При відносній вологості повітря 60% Маса пари в закритій посудині з водою складає 30 г. Скільки води належить випарувати, аби пара стала насиченою? [20 г] |
|
3.18. |
При температурі 20°С відносна вологість повітря дорівнює 40%. Визначити парціальний тиск водяної пари в повітрі. [935 Па] |
|
3.19. |
При температурі 17°С відносна вологість повітря дорівнює 80%. Визначити його абсолютну вологість. [≈12 г/м3] |
|
3.20. |
Визначити масу водяної пари в 2 м3 повітря при відносній вологості 60% і температурі 25°С. [27,6 г] |
| 3.21. |
Визначити парціальний тиск водяної пари в повітрі при відносній вологості 60% і температурі 40°С, якщо тиск насиченої пари при цій температурі складає 2 кПа? [1,2 кПа] |
| 3.22. |
В 4 м3 повітря міститься 40 г водяної пари. Визначити відносну вологість повітря, якщо його абсолютна вологість дорівнює 13,6 г/м3. [73,5%] |
Рівень Б
|
3.23. |
У циліндрі під поршнем міститься 20 дм3 насиченої пари при температурі 100°С. Визначити роботу, яку треба виконати, вдвічі зменшити об'єм під поршнем. [1 кДж] |
|
|
3.24. |
Визначити, яку частку (%) від загальної кількості в повітрі складають молекули води при нормальному атмосферному тиску та вологості 100% і температурі 30°С . [24%] |
|
|
3.25. |
Температура повітря 19°С, точка роси 8°С. Визначити абсолютну та відносну вологості повітря. [8,3 г/м3; ≈54% ] |
|
|
3.26. |
Повітря в кімнаті з температурою 16°С вологістю 60% поступово охолоджується. При якій температурі в кімнаті почнуть пітніти шибки? [≈8,5°С] |
|
|
3.25. |
Змішали 1 м3 повітря з відносною вологістю 20% та 2 м3 повітря з відносною вологістю 50% при однаковій температурі. Визначити вологість суміші. [40%] |
|
|
3.26. |
Визначити вологість повітря в циліндрі під рухомим поршнем при температурі 20°С і тиску 100 кПа, якщо при підвищенні тиску до 6 МПа й температури до 100°С в циліндрі з'являється вода. Тиск насиченої водяної пари при 20°С дорівнює 2,33 кПа. [≈72%] |
|
|
3.27. |
У вертикальному циліндрі з повітрям під рухомим поршнем масою 100 кг і площею перерізу 100 см2 міститься тонкий шар води масою 1 г. Визначити, на яку відстань переміститься поршень при нагріванні повтря до температури 150°С, при якій тиск насиченої водяної пари складає 477 кПа? Прийняти атмосферний тиск 100 кПа, g = 10 м/с2. [9,5 см] |
|
|
3.28. |
У посудину об'ємом 3 дм3 із сухим повітрям за нормальних умов вміщують 1 мл води, відтак герметично закривають і нагрівають до 90°С. Визначити тиск і вологість повітря, що встановляться в посудині. Тиск насиченої пари при 90°С складає 526 мм.рт.ст. [322 кПа; ≈11%] |
Поверхневі явища, капілярність
У текстах під діаметром трубки розуміється внутрішній діаметр, а діаметр шийки краплі при відриві приймається рівним діаметру отвору трубки.
Рівень А
|
3.29. |
Вода (поверхневий натяг σ = 73 мН/м) у відкриій капілярній трубці піднялася на висоту 6,6 см. Визначити діаметр трубки. [0,46 мм] |
|
|
3.30. |
Оцінити максимальний радіус капілярів у стовбурі дерева на висоті 10 м над землею. Поверхневий натяг води 73 мН/м. [1,5 мкм] |
|
|
3.31. |
Визначити масу краплин мікстури з коефіцієнтом поверхневого натягу 20 мН/м, які створюються піпеткою з діаметром отвору 1 мм. [6,4 мг ] |
|
|
3.32. |
Обчислити коефіцієнт поверхневого натягу олії (густина 0,9 г/см3), якщо за допомогою піпетки з діаметром отвору 1,2 мм у її об'ємі 4 см3 нарахували 240 крапель. [≈40 мН/м] |
|
|
3.33. |
Визначити а): молекулярний тиск у крапельці ртуті діаметром 1,5 мкм (поверхневий натяг 470 мН/м) і б) надлишковий тиск повітря всередині мильного пухирця діаметра 3 мм (поверхневий натяг мильного розчину 45 мН/м). [а) 12,5 ат; б) 6·10–4 ат (1ат = 100 кПа)] |
|
Рівень Б
|
3.34. |
На дні ставка утворився газовий пухирець діаметром 4 мкм. Визначити глибину ставка, якщо протягом спливання після відриву від дна до поверхні діаметр пухирця збільшився на 10%. Температура води по всій товщі однакова, атмосферний тиск 760 мм. рт. ст. [5 м] |
|
|
3.35. |
Запаяну з одного кінця капілярну трубку довжиною 11 см і діаметром 20 мкм, вертикально занурили в посудину з водою так, що рівні води в трубці та посудині зрівнялися. Атмосферний тиск нормальний. Визначити глибину занурення. [1,4 см ] |
|
3.36. |
Паралельні вертикальні скляні пластини нижніми краями торкаються поверхні води. Визначити висоту підйому води між пластинками при відстані між ними 0,5 мм.[3 см] ] |
|
|
3.37. |
Алюмінієве кільце радіусом 78 мм і масою 700 мг торкається поверхні мильної води (коефіцієнт поверхневого натягу 73 мН/м). Яким зусиллям можна відірвати кільце від розчину? [79 мН] |
|
|
3.38. |
Яку роботу необхідно виконати проти сил поверхневого натягу, аби вдвічі збільшити об’єм мильної бульбашки з початковим радіусом 1 см. Температура стала. [108 мкДж ] |
|
|
3.39. |
Укрита водою скляна пластинка внаслідок змочування "приклеїлась" до шибки. Вважаючи змочування повним, визначити, якою найменшою перпендикулярною до поверхні силою пластинку можна відірвати від шибки. Маса шару води між пластинкою та шибкою 100 мг, товщина 0,1 мм. [≈1,5 Н] |
Закон Гука, механічні властивості твердих тіл
У відповідях прийнято g = 10 м/с2.
|
3.40. |
Тягар, підвішений на сталевому дроті перерізом 2 мм2 розтягнув його на 0,5%. Визначити масу тягаря. Модуль Юнга для сталі 200 ГПа. [200 кг]. |
|
3.41. |
Визначити максимальну масу вантажу, який можна підвісити на мідному дроті діаметром 1 мм. Межа міцності міді 210 МПа. [16,5 кг] |
|
3.42. |
Визначити мінімальний діаметр сталевого троса, за допомогою якого можна піднімати вантаж масою 1 т із трикратним запасом міцності. Межа міцності сталі 470 МПа. [8 мм]. |
|
3.43. |
У старовину для вимірювання глибини дна моря використовували лот – тягар, підвішений на довгому тросі. Визначити максимальну глибину, яку можна виміряти лотом із сталевим (густина 7,8 г/см3) тросом із межею міцності 510 МПа. [7500 м] |
|
3.44. |
Мідну та залізну дротину з діаметром 1 мм і однаковою довжиною зварили встик і міцно закріпили за кінець. Визначити масу вантажу, який треба прикріпити, щоб утворений підвіс видовжився на 1%. Модулі Юнга міді та заліза дорівнюють 100 ГПа та 200 ГПа, відповідно. [≈105 кг] |
|
3.45. |
Горизонтальна залізобетонна плита масою 500 т спирається на 4 чавунні труби з товщиною 3 см і діаметром 30 см. Із яким запасом міцності "працюють" опори при граничній допустимій напрузі в чавуні 300 МПа. [3,7] |



 в середньому є компенсована. Але на молекули в поверхневому шарі з боку інших діє
в середньому є компенсована. Але на молекули в поверхневому шарі з боку інших діє 

 Ефекти змочування та незмочування спричинюють викривлення поверхні рідини біля стінки посудини, через що при змочуванні вона є угнутою (рис. 3.7а), а при незмочуванні – опуклою (рис. 3.7б). При цьому у вузькій циліндричній трубці поверхня рідини ("меніск") має форму сферичного
Ефекти змочування та незмочування спричинюють викривлення поверхні рідини біля стінки посудини, через що при змочуванні вона є угнутою (рис. 3.7а), а при незмочуванні – опуклою (рис. 3.7б). При цьому у вузькій циліндричній трубці поверхня рідини ("меніск") має форму сферичного  де R – радіус кривини поверхні меніска. Як випливає із сказаного вище,
де R – радіус кривини поверхні меніска. Як випливає із сказаного вище,