ФІЗИКА ДЛЯ БАКАЛАВРІВ. МЕХАНІКА
V. ДИНАМІКА ТВЕРДОГО ТІЛА
2. Динаміка твердого тіла
Як уже говорилося, в механіці тверде тіло трактується як сукупність малих частинок (матеріальних точок), взаємне розташування яких ні від чого не залежить. Через це сили взаємодії між окремими точками тіла ніяк не впливають на його механічний стан і в теорії взагалі не згадуються. Далі розглядаються:
2.1. Загальні рівняння динаміки твердого тіла
2.3. Рівняння динаміки обертального руху
2.4. Обчислення моменту інерції. Теорема Штайнера
2.5. Кінетична енергія твердого тіла
2.1. Загальні рівняння динаміки твердого тіла
Довільний рух твердого тіла можна розглядати як сукупність поступального та обертального рухів і описувати загальними рівняннями — рівнянням руху певної жорстко зв’язаної з тілом точки, що визначає поступальну складову руху, та рівняння моментів відносно цієї точки, яке визначає обертальну складову руху тіла.
Вибір указаної точки є довільним, але при складанні рівнянь руху слід ураховувати й сили інерції, позаяк система відліку, пов’язана з тілом, на загал є неінерціальною. Тому найзручнішим вибором є центр мас тіла, бо, як можна довести, сумарний момент сил інерції відносно центра мас завжди дорівнює нулю. У такому разі система загальних рівнянь динаміки твердого тіла складається з рівняння руху центра мас (розділІІІ, (2.5а)), та рівняння моментів (1.9):
|
\( m\vec{a}_c=\vec{F}\), \(\frac{\mathrm{d}\vec{L}}{\mathrm{d}t}=\vec{M} \), |
де \(\vec{F}\) – сума сил, які діють на тіло, а \(\vec{L} \) і \(\vec{M} \) – момент імпульсу тіла та сумарний момент діючих сил відносно центра мас.
Зауважимо, що при довільному русі тіла ці рівняння є дуже складними для розв’язування. Але задача значно спрощується, якщо тіло рухається вздовж заданої осі ОХ і обертається навколо перпендикулярної осі OZ, як це буває в технічних пристроях. У такому разі рівняння руху записують скалярно в проєкціях на осі:
|
\(m{{a}_{cx}}={{F}_{x}}\) |
(2.1) | |
|
\(\frac{\mathrm{d}L_z}{\mathrm{d}t}=M_z \). |
(2.2) |
При цьому алгебраїчні величини Lz та Mz називають моментами відносно осі OZ.
2.2. Моменти відносно осі
Момент імпульсу відносно осі. Момент інерції. Якщо тіло обертається навколо осі ОZ із кутовою швидкістю \(\vec{\omega }\), то всі його точки масами Δmі рухаються по колах відповідних радіусів Ri із швидкостями \( v_i=\omega R_i \) та імпульсами \(\vec{p}_i=\Delta{m}_i\vec{v}_i \), напрямки яких пов’язані з напрямом \(\vec{\omega }\) правилом правого гвинта, як показано на рис. 5.4 для точки, що лежить у площині рисунка. (Контур тіла на рисунку не зображено).
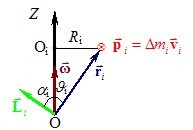
При цьому її вектор моменту імпульсу \(\vec{L}=\left[\vec{r}_i,\,\,\vec{p}_i\right] \) відносно якоїсь точки О на осі обертання лежить у площині рисунка. Тож відносно осі OZ момент імпульсу складає
\({{L}_{iz}}={{L}_{i}}\cos {{\alpha }_{i}}={{r}_{i}}\Delta {{m}_{i}}{{v}_{i}}\sin {{\vartheta }_{i}}=\Delta {{m}_{i}}{{v}_{i}}{{R}_{i}}=\Delta {{m}_{i}}{{v}_{i}}R_{i}^{2}{{\omega }_{z}}\)
де враховано, що вектори \(\vec{r}_i \) та \(\vec{p}_i \) є взаємно перпендикулярні, \({{\alpha }_{i}}=\left( 90{}^\circ -{{\vartheta }_{i}} \right)\) та \({{r}_{i}}\sin {{\vartheta }_{i}}={{R}_{i}}\).
Відтак момент імпульсу всього тіла відносно осі Z визначається як
|
\({{L}_{z}}=\left( \sum{\Delta {{m}_{i}}R_{i}^{2}} \right){{\omega }_{z}}\) |
(2.3) |
При цьому величина
|
\( {I}=\sum_{i}{\Delta {{m}_{i}}R_{i}^{2}}\) |
(2.4) |
називається моментом інерції І тіла відносно заданої осі.
Отже,
момент імпульсу твердого тіла відносно осі обертання дорівнює добутку його моменту інерції відносно цієї осі на проєкцію кутової швидкості:
|
\( L_z=I\omega_z \). |
(2.5) |
Збереження моменту імпульсу відносно осі. Поняття моменту імпульсу відносно осі зберігає зміст і для системи тіл, якщо вони обертаються навколо паралельних, осей, або однієї спільної осі. При цьому момент імпульсу системи відносно заданої осі OZ визначається як Lz = ∑Iiωzi. В такому разі, з рівняння моментів (2.2) випливає, що коли сумарний момент зовнішніх сил Мz = 0, то
\( \frac{\mathrm{d}L_z}{\mathrm{d}t}={0}\) \( \Rightarrow \) \( {L}_z=\mathrm{const} \),
тобто, сумарний момент імпульсу тіл системи відносно осі OZ зберігається. При цьому повний момент імпульсу \(\vec{L}=\sum_i\vec{L}_{i}\) може змінюватися з часом.
У розгорнутому вигляді і з урахуванням виразу (2.16) закон збереження моменту імпульсу відносно осі можна записати так:
|
\({I_1\omega_{z1}+I_2\omega_{z2}+...=I_1\omega'_{1z}+I_2\omega'_{z2}+...}\) |
(2.6) |
Величини в лівій та правій частині цього рівняння визначені для спільної осі ОZ і відносяться до двох довільних моментів часу.
Цікавий прояв закону збереження моменту імпульсу відносно осі обертання тіла спостерігається при зміні його моменту інерції під дією внутрішніх сил. У цьому випадку завдяки збереженню моменту імпульсу змінюється кутова швидкість обертання тіла:
|
\( {I}_1\omega_{1}=I_{2}\omega_{2}\) \( \Rightarrow \) \( \frac{\omega_{2}}{\omega_{1}}=\frac{I_{1}}{I_{2}}\). |
Цей ефект, зокрема, широко використовують спортсмени в різних видах спорту. До прикладу, для пришвидшення обертання фігуристка здіймає руки, зводячи їх над головою, або ж притискає їх до тіла, а для уповільнення – розводить в боки.
Цікава демонстрація американських астронавтів:
Момент сили відносно осі. Розглянемо тепер, як обчислюється момент сили Mz відносно закріпленої (фіксованої) осі обертання тіла. Нехай до деякої точки А тіла, що обертається навколо закріпленої осі OZ, прикладена довільна сила \(\vec{F}\) (рис. 5.5а).
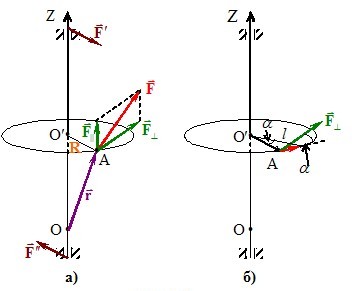
Силу \(\vec{F}\) можна розглядати як суму двох складових – перпендикулярної \( {\vec{F}}_{\bot}\) та паралельної \( {\vec{F}}_{\parallel}\) до осі обертання, так що \( \vec{F}=\vec{F}_{\bot}+\vec{F}_{\parallel}\). Неважко збагнути, що складова \({{\vec{F}}_{\bot }}\) обертає тіло навколо осі OZ, а \({{\vec{F}}_{\parallel }}\) намагається повернути саму вісь. Але, оскільки вісь обертання тіла є фіксованою, момент сили \({{\vec{F}}_{\parallel }}\) компенсується моментом сил реакції \({\vec{F}}'\) і \({\vec{F}}''\) у точках фіксації осі (підшипниках), тож силу \({{\vec{F}}_{\parallel }}\) можна не враховувати. Крім того, позаяк при переміщенні т. О по осі ОZ відстань О′А = l не змінюється (див рис. 5.5б), момент сили \( {\vec{F}}_{\bot}\), отже, і \(\vec{F}\), відносно осі не залежить від положення початку відліку і, згідно з означенням (1.6), визначається формулою:
|
\( M_z=\pm{F}_{\bot}\cdot{l}\), |
(2.7) |
де \( F_{\bot}\) – модуль сили \(\vec{F}_{\bot}\) і \( l \) – плече цієї сили відносно осі обертання, тобто, відстань між віссю обертання та лінією дії сили. Знак у виразі (2.7) збігається із знаком проєкції вектора \(\vec{M}'_{\bot}\) на вісь OZ. Цю формулу можна подати й інакше, якщо врахувати, що \( l=R\cos\alpha \), де α – кут між вектором \(\vec{F}_{\bot}\) й ортом \(\tau \) напрямку обертання точка А по колу, і що \( F\cos\alpha=F_{\tau}\) – то є проєкція сили \(\vec{F}_{\bot}\) (і \(\vec{F}\)) на орт \(\vec{\tau}\):
| \({{M}_{z}}={{F}_{\tau }}R \) | (2.7а) |
2.3. Рівняння динаміки обертального руху
Підставивши вираз (2.4) у рівняння моментів (2.2), отримаємо:
|
\(\frac{\mathrm{d}(I{\omega})}{\mathrm{d}t}=M_z \) \( \Rightarrow \) \( {I}\frac{\mathrm{d}\omega_z}{\mathrm{d}t}=M_z \), |
або
|
\({I\beta_z=M_z}\), |
(2.8) |
де \( I \) – момент інерції тіла відносно осі обертання, \(\beta_z \) – проєкція кутового прискорення на цю вісь.
Рівняння (2.8) як за формою, так і за змістом, є аналогом основного рівняння динаміки матеріальної точки (розділ ІІ, (1.5)) і називається основним рівнянням динаміки обертального руху твердого тіла. Воно дозволяє визначити кутове прискорення, а відтак за допомогою рівнянь кінематики (розділ І, (2.11) , (2.12)) — інші характеристики обертального руху твердого тіла.
З рівняння (2.8) випливає ще й те, що момент інерції тіла при обертальному русі відіграє таку саму роль, як маса при поступальному русі, тобто,
момент інерції є мірою інертності тіла щодо обертання навколо заданої осі.
При цьому така “обертальна” інертність залежить не тільки від маси тіла, а й від її розподілу відносно осі обертання.
Укажемо й на те, що рівняння (2.8) використовується замість загального рівняння моментів і при розгляді більш складних рухів твердого тіла за умови, що їхня обертова складова відбувається навколо незмінної за напрямом осі..
2.4. Обчислення моменту інерції. Теорема Штайнера
Згідно з формулою (2.15) момент інерції визначається не тільки величиною маси тіла, але й розташуванням окремих його частин відносно осі обертання, внаслідок чого момент інерції одного й того ж тіла має різні значення відносно різних осей. Тому для застосування рівняння (2.18) спочатку треба визначити момент інерції тіла відносно заданої осі.
Для довільного тіла ця задача аналітично не розв’язується, і момент інерції доводиться визначати дослідним шляхом. Але для тіл симетричної форми та із симетричним розподілом маси момент інерції можна обчислити. Для цього, найперше, треба взяти до уваги, що маса суцільного тіла неперервно розподілена по об’єму, і тому вираз (2.15) має тільки символічний зміст. Для реальних обчислень замість малих частинок тіла Δm треба розглядати елементарні маси dm, і дискретне додавання замінити інтегруванням:
|
\({I=\int{r^2\mathrm{d}m}=\int\limits_{V} r^2\rho(r)\mathrm{d}V}\), |
(2.9) |
де r – відстань від даної точки тіла до осі, відносно якої обчислюється момент інерції, ρ(r) – густина речовини тіла в даній точці, яка в загальному випадку може залежати від r, і dV – об’єм нескінченно малої ділянки тіла в околі даної точки.
Як приклад обчислимо момент інерції однорідного тонкого стрижня маси т і довжини \({l}\) відносно перпендикулярної до нього осі, що проходить через центр інерції О (центр мас), та відносно паралельної осі O′, що розташована на довільній відстані а від точки О (рис. 5.6).
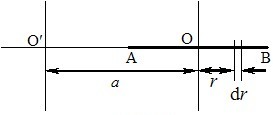
Напрямимо координатну вісь r уздовж стрижня й розмістимо початок відліку в його центрі мас О, тобто посередині. На довільній відстані r від початку відліку виділимо нескінченно малу ділянку стрижня довжини dr, маса якої дорівнює \(\mathrm{d}m=(m/l)\cdot\mathrm{d}r \). Тоді для осі О, згідно з (2.19), і, враховуючи координати кінців стрижня А та В, отримаємо:
|
\( I_0=\int r^2\mathrm{d}m=\frac{m}{l}\int\limits_{-\frac{l}{2}}^{\frac{l}{2}}r^2\mathrm{d}r=\frac{ml^2}{12}\). |
(2.9а) |
При обчисленні моменту інерції \({I}\) стрижня відносно осі O′ координата r відраховується від точки O′, тож \({r_A=a-l/2}\) і \({r_B=a+l/2}\). Отже,
\({I}=\int{r^2}\mathrm{d}m=\frac{m}{l}\int\limits_{a-\frac{l}{2}}^{a+\frac{l}{2}}r^2\mathrm{d}r=\frac{ml^2}{12}+ma^2 \).
У цьому виразі перший доданок – то є момент інерції стрижня \({I_0}\) відносно осі, що проходить через центр мас, тобто:
|
\( {I}={{I}_{0}}+m{{a}^{2}}\) |
(2.10) |
Можна довести, що цей результат є чинним і для будь-якого іншого тіла, незалежно від його форми. Він складає теорему Штайнера :
момент інерції довільного тіла відносно заданої осі дорівнює сумі його моменту інерції відносно паралельної осі, що проходить через центр мас, та добутку маси тіла на квадрат відстані між цими осями.
Ця теорема полегшує знаходження моментів інерції симетричних тіл відносно осей, паралельних до осей симетрії тіла.
На завершення наведемо вирази моментів інерції I0 деяких однорідних симетричних тіл відносно осей, що проходять через центр інерції і є осями симетрії тіла:
Табл. 1.
| Тіло | Вісь | Момент інерції I0 |
| Тонки стрижень довжини l | Перпендикулярна до стрижня | \(\frac{1}{12}ml^2 \) |
| Суцільний циліндр радіуса R | Співпадає з віссю циліндра | \(\frac{1}{2}mR^2 \) |
| Суцільна куля радіуса R | Проходить через центр кулі | \(\frac{2}{5}mR^2 \) |
| Суцільний однорідний конус із радіусом основи R | Співпадає з віссю конуса | \(\frac{3}{10}mR^2 \) |
2.5. Кінетична енергія твердого тіла
Окрім імпульсу та моменту імпульсу, важливою характеристикою стану руху твердого тіла є кінетична енергія, яка складається з кінетичних енергій всіх його точок. Але, позаяк різні точки твердого тіла рухаються не однаково, безпосередній розрахунок його кінетичної енергії в загальному випадку є неможливим. Виняток становлять тільки найпростіші рухи: поступальний, обертальний навколо фіксованої осі та рух, який є їхньою сукупністю.
Кінетична енергія поступального руху. Кінетична енергія є адитивною величиною і за будь-яких умов для твердого тіла визначається виразом:
|
\( K=\sum{\frac{\Delta {{m}_{i}}v_{i}^{2}}{2}}\) |
(2.11) |
де Δmi і vi – маси та швидкості окремих частинок тіла.
Позаяк при поступальному русі всі точки тіла, включно з центром мас, в кожен момент часу мають однакову швидкість vi = vс, і \(\sum{\Delta {{m}_{i}}=m}\), то кінетична енергія поступальнлього руху тіла
|
\({K}=\frac{m{{v}^{2}}}{2}\) |
(2.12) |
Кінетична енергія обертального руху. Якщо тіло обертається навколо нерухомої осі, всі його точки рухаються по колах відповідних радіусів Ri з однаковою кутовою швидкістю ω, і лінійними швидкостями vi = ωRi . Тому, згідно з (2.23), кінетична енергія тіла
|
\({{K}_{}}=\frac{1}{2}\left( \sum{\Delta {{m}_{i}}R_{i}^{2}} \right){{\omega }^{2}}\) |
Вираз у дужках є моментом інерції тіла I відносно осі обертання (див. (2.15)), отже,
кінетична енергія обертального руху твердого тіла визначається формулою
|
\({{K}_{об}}=\frac{{{I}_{c}}{{\omega }^{2}}}{2}\) |
(2.14) |
Урахувавши вираз (2.16), можна також записати:
|
\({{K}_{}}=\frac{L_{z}^{2}}{2I}\) |
(2.14а) |
Варто черговий раз звернути увагу на те, що ці формули теж можна отримати з відповідних формул механіки точки K = (mv2/2) i K = (p2/2m) заміною лінійних величин їхніми кутовими аналогами.
Кінетична енергія плоского руху. При плоскому русі (розділ І, п. 2.3) можна вважати, кожна точка Δmі твердого тіла рухається із швидкістю \(\vec{v}_{c}\) разом із центром мас і в той же час обертається навколо нього по колу в площини руху із якоюсь швидкістю \( \tilde{\vec{v}}_{i}\). Отже, в обраній системі відліку швидкість кожної точки складає \( \vec{v}_{i}=\tilde{\vec{v}}_{i}+\vec{v}_{c} \). Підставивши цей вираз у (2.20), отримаємо:
\( {K}_{\text{пл}}=\sum\frac{\Delta m_{i}\left( \vec{v}_{c}+\tilde{\vec{v}}_{i} \right)^{2}}{2}=\)
\(=\left( \sum\Delta m_i \right)\frac{v_c^2}{2}+\vec{v}_{c}\sum\Delta m_{i}\tilde{\vec{v}}_i+\sum\frac{\Delta m_{i}\tilde{\vec{v}}_{i}^{2}}{2}.\)
Оскільки \( \sum\Delta{m_{i}} \) – то є маса всього тіла т, перший доданок у цьому виразі визначає кінетичну енергію поступального руху \({K}\)пост = \( {mv}_{c}^{2}/{2}\). Другий доданок дорівнює нулю, бо включає вираз імпульсу тіла в відносно власного центра мас. Швидкості \({\tilde{v}_i}\) – це лінійні швидкості обертального руху точок тіла навколо фіксованої осі, що проходить через центр мас. Тому останній доданок визначає кінетичну енергію обертального руху тіла, і його можна замінити виразом (2.14). Таким чином для кінетичної енергії плоского руху тіла маємо:
|
\({{K}_{пл}}=\frac{mv_{c}^{2}}{2}+\frac{{{I}_{c}}{{\omega }^{2}}}{2}\) |
(2.15) |
де Iс – момент інерції тіла відносно осі обертання, що проходить через центр мас, \({v_c}\) – швидкість руху центра мас.
Кінетична енергія обертального руху та робота моменту сил. У розділі ІV, (формули (2.2), (2.2а)) було встановлено, що зміна кінетичної енергії точкового тіла дорівнює повній роботі сил, які діють на нього. Для протяжного твердого тіла ситуація є аналогічною. Розглянемо роботу, що виконується при обертанні тіла навколо нерухомої осі. В цьому випадку прикладена до нього сила \(\vec{F}\) є перпендикулярною до осі обертання. При елементарному повороті тіла на кут dφ точка прикладання сили А здійснює переміщення \({\mathrm{d}\vec{s}}\) по колу радіуса R (рис. 5.7), і сила виконує роботу \(\delta{A}=\vec{F}\cdot\mathrm{d}\vec{s}=F\mathrm{d}s\cos\alpha \).
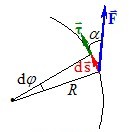
У цьому виразі ds = Rdφ і F cosα = Fτ – проєкція сили \(\vec{F}\) на дотичну до кола, по якому рухається точка А. Отже, врахувавши вираз (2.7а), маємо:
|
\(\delta{A}=F_{\tau}R\mathrm{d}\varphi \) \( \Rightarrow \) \( \delta{A}=M_z\mathrm{d}\varphi \). |
(2.16) |
|
При повороті на скінченний кут
|
\({A=\int\limits_0^{\varphi}M_z\mathrm{d}\varphi}\). |
(2.16а) |
Зв’язок між роботою моменту сил і кінетичною енергією обертального руху отримаємо після нескладних викладок, виразивши в (2.26), величину Mz із рівняння (2.18) і врахувавши співвідношення кінематики твердого тіла (2.5):
|
\( \delta{A}=M_{z}\mathrm{d}\varphi =I\beta_{z}\mathrm{d}\varphi =I\beta_{z}\omega_{z}\mathrm{d}{t}=I\omega_{z}\mathrm{d}\omega_{z}=\mathrm{d}\left(\frac{I\omega^{2}}{2}\right) \) \( \Rightarrow \) \( \delta{A}=\mathrm{d}K \)об. |
(2.17) |
При повороті на скінченний кут
|
\({A=\Delta{K}}\)об = \({K}\)об2 - \({K}\)об1. |
(2.17а) |
Отже, теорема про кінетичну енергію зберігає чинність і для обертального руху твердого тіла.
1. Що називається моментом імпульсу відносно осі? Якою формулою він визначається для твердого тіла?
2. Що таке момент інерції тіла? Який фізичний зміст вона має?
3. Чи має тіло заданий момент інерції? Чи є момент інерції відносно заданої осі у нерухомого тіла ?
4. У чому полягає теорема Штайнера? Яке вона має практичне призначення?
5. Як пов’язані між собою моменти сили відносно заданої осі відносно точки, розташованої цій осі?
6. Що таке плече сили? Чи можна сказати, що модуль моменту сили відносно осі дорівнює добутку модуля сили на її плече?
7. Чи можна твердити, що під дією заданої сили більш масивне тіло отримає менше кутове прискорення, ніж менш масивне? Чому?
8. Суцільний і порожнистий циліндри однакового радіуса та маси одночасно починають скочуватися з вершини похилої площини. Чи одночасно вони досягнуть основи площини? Якщо ні, то який і чому відстане?
9. Коли виконується та як записується закон збереження моменту імпульсу відносно осі? Наведіть прояви цього закону.
10. Запишіть вирази кінетичної енергії тіла, що обертається навколо нерухомої осі.
11. Запишіть вирази кінетичної енергії тіла, що здійснює плоский рух.
12. Колесо рівномірно котиться без ковзання так, що кутова швидкість його обертання складає ω. Визначити кінетичну енергію колеса, якщо воно має масу m і момент інерції відносно власної осі Iс.
13. Як обчислюється робота моменту сили?