ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв’язування задач
Прямолінійний рух одного тіла та зв'язаних тіл
Рівень А
|
2.21. |
Двоє хлопчиків тягнуть за динамометр у протилежні боки із силою F = 100 Н кожен. Що показує динамометр? [100 Н] |
|
2.22. |
Через блок перекинуто нитку з прив'язаними гирями масою по 0,5 кг . Визначити силу натягу нитки.[5 Н] |
|
2.23. |
З якою силою притягаються один до одного два штучні супутники Землі масою 2,5 т кожен при наближенні один до одного на відстань 100 м? [≈42 нН] |
|
2.24. |
Визначити масу гирі, яку треба підвісити до пружини, аби вона розтяглася на 3 см. Жорсткість пружини 900 Н/м. [2,7 кг] |
|
2.25. |
Маса легковика m1 = 1 т, а вантажівки m2 = 8 т. Визначити відношення їхніх прискорень a1/a2, якщо сила тяги двигуна у вантажівки вдвічі більша, ніж у легковика. [4] |
|
2.26. |
Після того, як дві заряджені кульки поклали на гладку горизонтальну поверхню й відпустили, вони почали розлітатись із прискореннями a1 = 1 см/с2 і a2 = 1 м/с2. Як співвідносяться їхні маси? [(m1/m2) = 100] |
|
2.27. |
Яка сила має діяти на тіло масою 5 кг, аби воно рухалося вертикально вниз з прискоренням 3 м/с2? [35 Н] |
|
2.28. |
Під дією деякої сили одне тіло рухається з прискоренням 2,0 м/с2 , а інше — 3,0 м/с2. З яким прискоренням рухатимуться тіла під дією цієї сили, якщо їх з'єднати? [1,2 м/с2] |
|
2.29. |
Яким буде прискорення автомобіля на горизонтальній дорозі після вимикання двигуна при коефіцієнті опору μ ? [–µg ] |
|
2.30. |
Брусок рівномірно тягнуть за мотузку по горизонтальній дошці, прикладаючи поздовжню силу 1,5 Н. Визначити вагу бруска, якщо коефіцієнт тертя між ним і дошкою дорівнює 0,3. [5 Н] |
|
2.31. |
Авто рухається з прискоренням 0,6 м/с2. Визначити, яким воно стане після вимикання двигуна, якщо середня сила опору складає 25% сили тяги двигуна. [–0,2 м/с2] |
|
2.32. |
Тіло вільно ковзає з прискоренням 25 см/с2 по гладкій похилій площині. Знайти її кут нахилу до горизонту. [14,5°] |
|
2.33. |
Під яким кутом до горизонту встановиться поверхня води у відрі на візку, коли він почне рухатися горизонтально з прискоренням 1,5 м/с2?[\(\approx{8,5}^{\circ}\)] |
|
2.34. |
Знайти величину та напрям прискорення літака масою 20 т при злеті, якщо на мить відриву від злітної смуги підйомна сила крил дорівнювала 207 кН, а сили тяги двигуна та опору, відповідно, 20 кН і 10 кН. [≈0,6 м/с2; 35° до горизонту] |
Рівень Б
|
2.35. |
Через блок перекинули нитку з двома гирями масою по 200 г на кінцях. Яку вертикальну силу треба прикласти до однієї з гир, аби вона почала рухатись з прискоренням 50 см/с2? [0,2 Н] |
|
2.36. |
Два тягарці масою по 120 г висять на одному рівні на нитці, що перекинута через блок. Знайти відстань, на яку вони розійдуться та якої швидкості набудуть протягом 2 с, якщо за один потягти вниз із сталою 48 мН. [80 см; 40 см/с] |
|
2.36. |
Людина жердиною відштовхує від причалу баржу масою 300 т, прикладаючи протягом 30 c зусилля 400 Н. На яку відстань від причалу відійде баржа за цей час ? [0,6 м] |
|
2.37. |
Тіло масою 2 кг рухається з прискоренням 15 см/с2 по горизонтальній поверхні з коефіцієнтом тертя 0,05. Знати прикладену до тіла силу, коли вона діє: а) горизонтально; б) вгору під кутом 30° до горизонту? [1,3 H; 1,46 H] |
|
2.38. |
Тілу, що лежить на горизонтальній поверхні, поштовхом надали швидкості 3 м/c. Визначити коефіцієнт тертя між тілом та поверхнею, якщо воно пройшло до зупинки шлях 3 м. [0,15] |
|
2.39. |
Аби магніт масою 50 г, що "прилип" до вертикальної сталевої плити, рівномірно ковзав униз, до нього треба прикласти вздовж плити силу 1,5 H. Визначити: а) силу тиску магніту на плиту; б) силу, потрібну для рівномірного пересування магніту вгору. Коефіцієнт тертя між магнітом і плитою 0,2. [10 H; 2,5 H] |
|
2.40. |
Автомобіль рухається з незмінною швидкістю 72 км/год спочатку за, а потім проти вітру, швидкість якого дорівнює 15 м/с. У скільки разів сила опору повітря на зворотньому шляху є більшою, якщо вона лінійно залежить від швидкості автомобіля відносно повітря. [49] |
|
2.41. |
Вантаж масою 1,0 кг лежить на похилій площині. Яка сила тертя діє на нього, якщо нормальна реакція площини складає 6,0 Н. [8 Н] |
|
2.42. |
По похилій площині, нахиленій під кутом \(\alpha\) до горизонту, тіло ковзає рівномірно. За який час t воно зісковзне з висоти h, рухаючись по такій самій площині нахиленій до горизонту під кутом \(\beta\) ? $\left[ t=\sqrt{\frac{2h}{g}\cdot \frac{\cos \alpha }{\sin \beta \sin \left( \beta -\alpha \right)}},\quad \beta >\alpha \right]$ |
|
2.43. |
Визначити, за який час тіло зісковзує з гірки з кутом нахилу до горизонту 45° і висотою h = 2 м, якщо граничний кут нахилу, при якому тіло ще перебуває в рівновазі, складає 30°. [≈1,4 c] |
|
2.44. |
Тіло зісковзує без тертя з вершини похилої площини. При цьому його середня швидкість за перші 0,5 с є на 2,45 м/с менша, ніж за перші 1,5 c. Знайти кут нахилу площини до горизонту. [30°] |
| 2.45. |
Аби утримувати сани на схилі гори з ухилом 0,2, треба прикладати вздовж схилу силу 50 Н, а щоби рухати їх угору, її необхідно збільшити на 100 H. З яким прискоренням почнуть спускатися сани, якщо їх вивільнити? [0,1 м/с2] |
| 2.46. |
Тіло лежить на довгій дошці, нахиленій під кутом \(4^{\circ}\) до горизонту. Визначити: а) граничне значенні коефіцієнта тертя, при якому тіло почне ковзати по площині; б) прискорення тіла та час проходження ним відстані 10 м при коефіцієнті тертя 0,03; в) швидкість тіла наприкінці спуску. [а) 0,07; б) 0,39 м/с2, 22,6 с; в) 2,8 м/с] |
| 2.47 |
|
|
2.48. |
До одного з двох з'єднаних ниткою брусків масами 2 кг і 3 кг, які знаходяться на горизонтальній поверхні з коефіцієнтом тертя 0,4, прикладено силу 40 H під кутом \(30^{\circ}\) до горизонту. Визначити прискорення брусків і натяг нитки, якщо силу прикладено: а) до першого; б) до другого бруска. [а) 4,5 м/с2, 25,5 Н; б) 4,5 м/с2, 17,0 Н] |
|
2.49 |
Через блок перекинуто нитку з прикріпленими до кінців важками. Знайти відношення мас важків, якщо вони рухаються з прискоренням a = 0,2g (g – прискорення вільного падіння). [2 : 3] |
|
2.50. |
Мідний (ρ = 9 г/см3) брусок довжиною L = 50 см горизонтально рухається у поздовжньому напрямі з прискоренням a = 2 м/с2 . Знайти механічну напругу σ, що виникає в бруску на відстані l = 30 см від переднього кінця. [σ = ρ(L – l)a = 3,6 кПа] |
|
2.51. |
На початку підйому та спуску ліфт має однакове прискорення. Знайти його величину, якщо вага людини при цьому відрізняється в 3 рази? [4,9 м/с2] |
|
2.52. |
До стелі ліфта, що рухається рівноприскорено, на мотузці підвішено тіло масою 1 кг, з'єднане ниткою з тілом маси 2 кг. Знайти натяг мотузки, якщо натяг нитки складає 10 H. [15 H] |
Рівень В
|
2.53. |
М’яч вільно падає з великої висоти на горизонтальну поверхню й пружно (без утрати швидкості) відбивається. Знайти прискорення м’яча одразу після відскоку. [$2\vec{g}$] |
|
2.54. |
Спринтер прискорюється тільки на перших 20 м стометрівки. При якому коефіцієнті зчеплення (тертя) k взуття з біговою доріжкою він не зможе подолати дистанцію краще, ніж за 12 с? [k < 0,14] |
|
2.55. |
По похилій площині з кутом нахилу \(20^{\circ}\) до горизонту пускають вгору кульку масою 100 г. Визначити силу опору, що діє на кульку, якщо час її спуску є вдвічі більший, ніж час підйому. [6 H] |
|
2.56. |
На похилій площині з кутом нахилу \(\alpha\) до горизонту і коефіцієнтом тертя \(\mu\) лежить ящик маси m. Яку величину має мати і під яким кутом β до площини бути спрямована найменша сила Fmin , потрібна для пересування ящика вгору? $\left[ {{F}_{\min }}=\frac{mg\left( \sin \alpha +\mu \cos \alpha \right)}{\sqrt{1+{{\mu }^{2}}}};\quad \beta =\operatorname{arctg}\mu \right]$
|
|
2.57. |
Бруски з масами m1 = 1 кг і m2 = 1,5 кг знаходяться на горизонтальній поверхні (рис. 2.57). Коефіцієнт тертя між брусками \(\mu_{1}=0,4\), а між бруском m2 і поверхнею \(\mu_{2}=0,1\). З яким прискореннями рухатимуться бруски під дією сили F = 5 H, яка є прикладена під кутом $\vartheta $ = 30° до горизонту? [1,33 м/с2; 0,33 м/с2;] . |
|
2.58. |
Два бруски лежать один на одному. Маса верхнього бруска 2 кг, нижнього – 1 кг. Коефіцієнт тертя між брусками 0,25, а між нижнім поверхнею 0,5. З яким прискоренням верхній брусок буде рухатись відносно нижнього та відносно поверхні стола, якщо до нижнього прикласти горизонтальну силу 20 H.? [2,5 м/с2; 7,4 м/с2] |
|
2.59. |
На краю дошки масою 1 кг, яка лежить на гладкій горизонтальній поверхні, знаходиться брусок маси 200 г. Яку силу необхідно прикласти до бруска вздовж дошки, аби він зіскочив на момент, коли дошка переміститься на чотири довжини? Коефіцієнт тертя між бруском і дошкою 0,6. [1,5 H] |
|
2.60. |
Аби зрушити ящик масою M, людина масою m тягне його на себе під кутом до горизонту. Коефіцієнти тертя між підлогою та ящиком і між людиною та підлогою однакові й становлять \(\mu\). Яку силу має прикладати людина, аби тягти ящик? $\left[ F\ge \left( {g}/{2}\; \right)\sqrt{{{\mu }^{2}}{{\left( M+m \right)}^{2}}+{{\left( M-m \right)}^{2}}} \right]$ |
|
2.61. |
|
|
2.62. |
$\left[ {{a}_{1}}=\frac{\left| 2{{m}_{1}}-{{m}_{2}} \right|}{2{{m}_{1}}+\left( {{{m}_{2}}}/{2}\; \right)}g;\quad {{a}_{2}}=\frac{{{a}_{1}}}{2} \right]$
|
|
2.63. |
$\left[ \frac{4{{m}_{1}}{{m}_{2}}+{{m}_{0}}\left( {{m}_{1}}-{{m}_{2}} \right)}{{{m}_{1}}{{m}_{2}}+{{m}_{0}}\left( {{m}_{1}}+{{m}_{2}} \right)} \right]$g
|
|
2.64. |
На двох зіставлених похилих площинах із кутами нахилу 45° і 30° до горизонту знаходяться два однакові тягарці масою по 1 кг, які зв'язані ниткою, що перекинута через блок у вершині площин. Коефіцієнт тертя між тягарцями та площинами складає 0,1. Визначити: а) прискорення тягарців; б) силу натягу нитки; в) сила реакції осі блока. [а) 0,25 м/с2; б) 6 Н; в) 7,5 Н] |
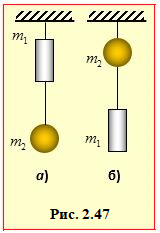 Два зв'язані ниткою тягарці
Два зв'язані ниткою тягарці 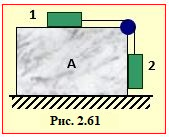
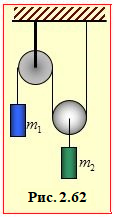 Визначити прискорення вантажів m1 і m2 у системі блоків рис. 2.
Визначити прискорення вантажів m1 і m2 у системі блоків рис. 2.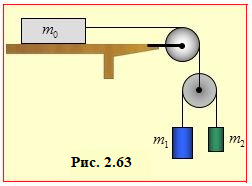 У системі, що показана на рис. 2.
У системі, що показана на рис. 2.