ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
2. Приклади розв'язування задач
Рух тіла, що кинуте під кутом до горизонту
Рівень А
|
1.127. |
Два тіла кинуто з однієї точки з однаковою швидкістю під кутами \(30^{\circ}\) і \(60^{\circ}\) до горизонту. Визначити відношення максимальних висот підйому та дальностей польоту тіл. [3; 1] |
|
1.128. |
М'яч, який кинуто горизонтально з висоти 2 м над землею, упав на землю на відстані 7 м по горизонталі. Визначити 1) початкову і 2) кінцеву швидкості м'яча. [ 1) ≈11 м/с; 2) ≈13 м/с] |
|
1.129. |
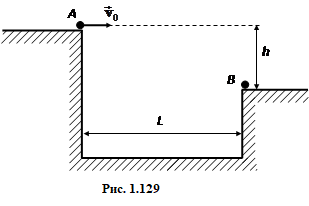
При якій швидкості v0 у точці A (рис. 1.129) мотоцикліст перелетить у точку В при L = 3 м і h = 1,125 м? [6 м/с]
|
|
1.130. |
Тіло кинули із землі під кутом \(30^{\circ}\) до горизонту з початковою швидкістю 100 м/с. Через який час тіло опиниться на на висоті 50 м? [≈1 с; ≈9 c] |
Рівень Б
|
1.131. |
М'яч кинули з землі під кутом \(30^{\circ}\) до горизонту з початковою швидкістю 10 м/с. Визначити: а) горизонтальну та вертикальну складові початкової швидкості м'яча; б) час його руху; в) висоту підйому і дальність польоту. [ а) \(\approx{8,7}\) м/с, 5 м/с; б) 1 с; в) \(\approx{1,3}\) м, \(\approx{8,7}\) м] |
|
1.132. |
Тіло кинули з поверхні землі під кутом \(60^{\circ}\) до горизонту з початковою швидкістю 20 м/с. Визначити наступні характеристики руху тіла: а) рівняння траєкторії y(x); б) час руху; в) найбільшу висоту підйому; г) дальність польоту; д) напрям його руху через 1 c після кидка. [a) y = 1,73x – 0,05x2; б) 3,46 с; в) 15 м; г) с; д) 34,6 м; е) \(47^{\circ}\) до до горизонту] |
|
1.133. |
Двоє хлопчиків перекидаються м'ячем. Якою є максимальна висота підйому м'яча над точкою кидання, якщо він перебуває в польоті 2 c? [5 м] |
|
1.134. |
Тіло з висоти 30 м кинули вниз під кутом \(30^{\circ}\) до горизонту зі швидкістю 10 м/с. Визначити: а) час польоту; б) горизонтальну дальність польоту; в) величину та напрям швидкості тіла на момент падіння. [а) 2 с; б) 17,3 м; в) ≈26,5 м/с, \(71^{\circ}\) до горизонту] |
|
1.135. |
Камінь, який кинуто горизонтально зі швидкістю 15 м/с, впав на землю під кутом \(60^{\circ}\) до горизонту. З якої висоти було кинуто камінь та на якій відстані по горизонталі від точки кидання він впав на землю? [≈34 м; ≈40 м] |
|
1.136. |
Снаряд, випущений під кутом \(30^{\circ}\) до горизонту, побував на деякій висоті двічі: через 3 c і 5 c з моменту пострілу. Визначити початкову швидкість та максимальну висоту підйому снаряда. [80 м/с; 80 м] |
|
1.137. |
Хлопчик, який стоїть на схилі гори з кутом нахилу до горизонту \(30^{\circ}\), кидає в напрямку вершини камінь під кутом \(60^{\circ}\) до горизонту. На якій відстані від хлопчика камінь впаде на схил при швидкості кидка 10 м/с? [≈7 м] |
|
1.138. |
Тіло кинуто з поверхні землі з початковою швидкістю 10 м/с. На якій відстані тіло впаде якщо за 0,5 c від початку руху його швидкість зменшилася до 7 м/с. [≈10 м] |
Рівень В
|
1.139. |
Частинка рухається по траєкторії y = 1,732x – 2x2 із прискоренням, проєкції котрого складають aх = 0 і ay = –10 м/с2. Визначити, з якою швидкістю частинка пройшла початок координат. [4,47 м/с] |
|
1.140. |
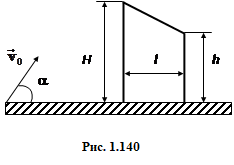
З якою мінімальною швидкістю v0, під яким кутом α та з якої відстані L слід кидати камінь, аби він перелетів через будівлю, профіль якої подано на рис. 1.140.[ v0 = \(\sqrt{g\left(\frac{l^{2}}{2(H-h)}\right)}\); α = \(\mathrm{arctg}\left(\frac{\sqrt{4H(H-h)}}{l}\right)\); L = \(l\sqrt{H/(H-h)}\)].
|
|
1.141. |
На кинуту з землі під кутом \(\varphi\) до горизонту легку кульку, діє вітер, який надає їй сталого горизонтального прискорення а. На скільки η% він змінить дальність польоту кульки? [η = (a·tgφ/g)·100%] |
|
1.142. |
Зі шланга, що лежить на землі, неперервно б'є струмінь води під кутом 45° до горизонту. Яка маса води знаходиться в повітрі, якщо швидкість вильоту води 10 м/с і площа перерізу шланга 5 см2? [7 кг] |
|
1.143. |
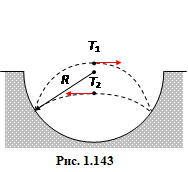
Унаслідок зіткнень із стінкою, кулька перескакує від одного до іншого боку півсферичної лунки (рис.1.143). Зіткнення відбуваються на одному рівні й абсолютно пружно (без утрати швидкості). Визначити радіус лунки, якщо час перельоту кульки від стінки до стінки в один бік складає T1, а в інший − T2. $\left[ \ \frac{g{{T}_{1}}{{T}_{2}}}{2\sqrt{2}}\ \right]$
|