ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
2. Приклади розв'язування задач
Кінематика руху з постійним прискоренням
Рівень А
|
1.63. |
Які з наведених рівнянь описують рух тіла зі сталим прискоренням? 1) vx = 5 – 5t; 2) ax = 0,25t; 3) x = 2t2; 4) vx = –8t +7; 5) vx = 0,8t; 6) x = 12 – 4t + 0,2t2; 7) x = 2t3 – 8t; 8) \(a_{x}=\sqrt{4t}\). [1); 3); 4); 6)] |
|
1.64. |
За час 1 мс швидкість ракети збільшилася на 5 см/с. Визначити прискорення ракети. [50 м/с2] |
|
1.65. |
На фініші дистанції велосипедист за 5 c збільшив швидкість від 27 км/год до 36 км/год. Визначити прискорення велосипедиста. [0,5 м/с2] |
|
1.66. |
Потяг починає рух із прискоренням 0,2 м/с2. Визначити його швидкість через t1 = 0,5 хв та t2 = 1,0 хв. [6 м/с; 12 м/с] |
|
1.67. |
Вагонетка починає рухатися з прискоренням 25 см/с2. Визначити швидкість вагонетки через 10 с після початку руху та її середню швидкість за цей час. [2,5 м/с; 1,25 м/с] |
|
1.68. |
Потяг починає гальмування із прискоренням –0,3 м/с2 і зупиняється через 1 хв. Визначити початкову швидкість потяга. [65 км/год] |
|
1.69. |
Куля, що котиться підлогою зі швидкістю 0,64 м/с, починає сповільнюватися з прискоренням –6 см/с2. Визначити час руху та пройдений кулею шлях до зупинки. [4 с; 1,28 м] |
|
1.70. |
Куля, що скочується похилим жолобом, за 5 c проходить шлях 75 см. Знайти прискорення кулі. [6 см/с2] |
|
1.71. |
Космічна ракета стартує з навколоземної орбіти при швидкості 7,9 км/с і на шляху 3000 км розганяється до швидкості 11,2 км/с. Визначити прискорення та час розгону ракети. [10,5 м/с2; 5,24 хв] |
|
1.72. |
Трасу швидкісного спуску довжиною 1000 м гірськолижник долає за 60 с. Визначити його швидкість на фініші та середню швидкість на дистанції, вважаючи рух рівноприскореним. [120 км/год; 60 км/год] |
|
1.73. |
При швидкості v = 43,2 км/год гальмівний шлях автобуса дорівнює S = 54 м. Визначити час екстреного гальмування автобуса при вказаній швидкості. [9 с] |
|
1.74. |
На підході до світлофора тепловоз протягом 10 с зменшив швидкість від 90 км/год до 36 км/год. Визначити, на якій відстані від світлофора та з яким прискоренням почав гальмування тепловоз. [175 м; –1,5 м/с2] |
|
1.75. |
Камінь, що падає з прямовисного урвища на березі річки, досягає води за 3 c. Зайти висоту урвища та швидкість каменя на момент падінні у воду. [45 м; 30 м/с] |
|
1.76. |
М'яч, кинутий вертикально вгору, впав на землю через 3 c. Визначити початкову швидкість м'яча. [15 м/с] |
|
1.77. |
Парашутист у стрибку з висоти 200 м розкриває парашут із затримкою 5 с. Визначити швидкість парашутиста та відстань до землі на момент розкриття парашута. [ 50 м/с; 75 м] |
|
1.78. |
Моторний човен спочатку протягом 10 c рухався рівномірно зі швидкістю 5 м/с, а потім ще 5 с – із прискоренням 1,0 м/с2. Який шлях пройшов човен за весь час? [87,5 м]. |
|
1.79. |
Моторолер починає розганятися з місця з прискоренням 1,0 м/с2. Якої швидкості він набуде на шляху 200 м? [72 км/год] |
|
1.80. |
На якому шляху авто, маючи прискорення 2,0 м/с2, розженеться від швидкості 36 км/год до 108 км/год? [200 м] |
|
1.81. |
Авто, рухаючись з прискоренням 2,0 м/с2, за час 5 c пройшло шлях 125 м. Визначити його початкову швидкість. [20 м/с] |
|
1.82. |
З яким прискоренням має рухатися локомотив, аби на шляху 500 м збільшити швидкість від 18 км/год до 36 км/год? [7,5 см/с2] |
|
1.83. |
При забиванні палі молот вільно падає на неї з висоти 5 м. Визначити швидкість молота на момент удару. [10 м/с] |
|
1.84. |
Яструб, який полює здобич, у вільному падінні наздоганяє її, маючи швидкість 100 м/с. З якої висоти він почав атаку? [0,5 км] |
|
1.85. |
У скільки разів треба збільшити початкову швидкість кинутого вгору м'яча, аби збільшити у два рази: а) час його повернення; б) висоту підйому ? [2; $\sqrt{2}$] |
Рівень Б
| 1.86. |
Чи можна сказати, що коли відстань між двома рухомими тілами залишається незмінною, то вони рухаються: а) рівномірно; б) з однаковою за величиною швидкістю; в) з однаковою за напрямом швидкістю? [а) так; б) ні; в) так] |
|
1.87. |
За наведеними рівняннями координати х(t) визначити прискорення ax(t) та там, де не задано, рівняння швидкості vx(t) для тих точок, які здійснюють рівнозмінний рух: а) x = –2 + 2t – 4t2; б) v = 3 + 4t2; в) vх = 1 + 2t – 3t2; г) vх = 1 – 0,01t; д) x = 2t2. [а) –8 м/с2, vх = 2 – 8t; г) –0,01 м/с2; д) vх = 4t; 4 м/с2] |
|
1.88. |
Рівняння руху тіла вздовж осі OX має вигляд: x = 5+ 12t – 4t2. Визначити: а) швидкість тіла на момент t0 = 3 c; б) момент, коли тіло змінює напрям руху; в) момент повернення тіла в точку x = 0; г) швидкість тіла в точці x = 0. [а) –12 м/с; б) 1,5 с; в) 3,375 с; г) –15 м/с] |
|
1.89. |
Куля, що летить зі швидкістю 400 м/с, ударяє в земляний вал і заглиблюється в нього на 36 см. Визначити: а) час руху кулі у землі; б) прискорення кулі; в) швидкість кулі на глибині 18 см; г) глибину, на якій швидкість кулі буде втричі менша за початкову. [а) 1,8 мс; б) –221 км/с2; в) 282 м/с; г) 32 см] |
|
1.90. |
Швидкість літака при посадці складає 270 км/год, шлях пробігу – 1,0 км. Визначити прискорення та час гальмування літака. [≈ –2,8 м/с2; ≈ 27 c] |
|
1.91. |
Потяг починає гальмування при швидкості 72 км/год і проходить до зупинки 1 км. Визначити: а) прискорення потяга; б) час гальмування; в) швидкість потяга біля світлофора, встановленого на середні гальмівного шляху. [а) –0,2 м/с2; б) ≈1,7 c; в) 14 м/с] |
|
1.92. |
Тіло, що починає рухатись із сталим прискоренням, за восьму секунду проходить відстань 30 м. Знайти величину прискорення тіла та відстань, яку воно проходить за п'ятнадцяту секунду руху. [4 м/с2, 58 м] |
|
1.93. |
Тіло починає рухатися прискорено й за шосту секунду проходить відстань 12 м. Визначити прискорення тіла та шлях, який воно подолає за 6 с. [≈2,2 м/с2; ≈39 м] |
|
1.94. |
Кинуте вгору тіло через 10 с падає зі швидкістю 20 м/с. Визначити швидкість кидка. [80 м/с] |
|
1.95. |
З даху будинку висотою 28 м кинули вгору камінь зі швидкістю 8 м/с. Визначити, з якою швидкістю камінь упаде на землю. [25 м/с] |
|
1.96. |
З гелікоптера, що завис, з інтервалом 1 с скинули без початкової швидкості два вантажі. Визначити відстань між вантажами через t1 = 2 c та t2 = 4 c після початку падіння першого вантажу. [15 м; 35 м] |
|
1.97. |
Людина, котра з краю прямовисного урвища відпустила камінь, почула звук падіння через 6 c. Визначити глибину урвища, прийнявши швидкість звуку 330 м/с. [≈150 м] |
|
1.98. |
З повітряної кулі, що опускається зі швидкістю 2 м/с, кинули вгору камінь зі швидкістю 18 м/с відносно землі. Визначити: а) відстань між каменем та кулею на момент, коли камінь підніметься на максимальну висоту над землею; б) через який час після кидка камінь пролетить повз кулю. [≈20 м; 4 с] |
|
1.99. |
З аеростата, що підійматися із землі з прискоренням 2 м/с2, через 5 c після початку підйому скинули баласт без початкової швидкості відносно аеростата. Через який час після скидання баласт впаде на землю? [3,2 c] |
|
1.100. |
Тіло кинули із землі вертикально вгору з початковою швидкістю 30 м/с. Через який час воно опиниться на висоті 25 м? [1 c, 5 c] |
|
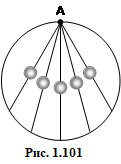
1.101. |
У вертикальній площині розташовано дротяне кільце діаметра d із спицями,на які нанизано намистинки, що можуть ковзати без тертя з т. А (рис. 1.101). Визначити, які з них зісковзнуть найшвидше? за який час τ? [всі за однаковий час τ =\(\sqrt{2d/g}\) ]
|
Рівень В
|
1.102. |
Тіло рухається за законом \(\vec{r}=\vec{b}t(1-ct)\), де \(\vec{b}\) – радіус-вектор, \(\vec{b}\) і c – задані сталі. Визначити пройдений тілом шлях S та його середню швидкість за час від початкового моменту до повернення у вихідне положення. [S = (b/2c); $\left\langle v \right\rangle $ = b/2] |
|
1.103. |
За час \(\tau\) тіло пройшло шлях S, збільшивши за цей час швидкість у n разів. Визначити прискорення тіла. $\left[ a=\frac{n-1}{n+1}\cdot \frac{2S}{{{\tau }^{2}}} \right]$ |
|
1.104. |
Перший вагон потяга, що рухається рівносповільнено, проходить повз спостерігача на пероні за 1 c, а другий – за 1,5 c. Визначити прискорення та початкову швидкість потяга, якщо |
|
1.105. |
Тіло, що вільно падає, останні 30 м шляху проходить за 0,5 c. Знайти: а) висоту падіння тіла; б) час проходження першого та останнього метра шляху; в) шлях, пройдений за першу та за останню секунду руху; г) середню швидкість на другій половині шляху. [а) ≈195 м; б) ≈0,45 с; 0,016 с; в) 50 м; 57,5 м; г) 53,3 м/с] |
|
1.106. |
Сигнальна ракета, вертикальна запущено із землі, за час згоряння заряду протягом 2 с набула прискорення a = 2g. Визначити: а) максимальну висоту і час підйому ракети та б) час її падіння на землю. [а) 120 м, 6 с; б) 4,9 с] |
|
1.107. |
Тіло, яке кинуто вертикально вгору, на висоті h = 10 м побувало двічі з інтервалом \(\tau=1,5\) c. Визначити: а) початкову швидкість тіла; б) тривалість руху. [16 м/с; 3,2 с] |
|
1.108. |
Авто рівномірно проходить відстань 450 м, а потім гальмує до зупинки із прискоренням –2 м/с2. Визначити: а) швидкість рівномірного руху, при якій загальний час руху буде найменшим; б) його величину; в) шлях, пройдений під час гальмування. [30 м/с; 30 с; 225 м] |
|
1.109. |
При якому нахилі даху будинку дощова вода стікає з нього якнайшвидше? Тертя не враховувати. [ \(45^{\circ}\) ] |
|
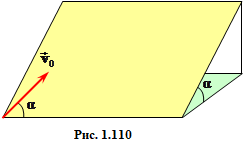
1.110. |
По гладкій площині, що нахилена під кутом \(\alpha=45^{\circ}\) (рис.1.110), під таким самим кутом до ребра пускають кульку з початковою швидкістю v. На якій відстані від початкового положення кулька знов опиниться на ребрі? [ \(\sqrt{2}v^{2}/g\) ]
|